2. 山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045
2. Key Lab of New Technology for Construction of Cities in Mountainous Area (Chongqing University), Ministry of Education, Chongqing 400045, China
大量实际震害表明,坡地、凸起地形、凹地等复杂地形均会对地震动产生不利影响,不同复杂地形的地震动研究越来越受到关注[1],目前众多学者对其作了大量研究.文献[2-3]对凸起地形地震动谱特性的影响作了研究,给出受地形影响的地面运动的位移傅里叶谱比规律和台地地形对地震地面运动特征周期的影响规律;文献[4-5]对局部复杂不规则地形地震动特性作了研究,发现复杂地形地震动放大效应要大于单一地形;文献[6-7]对不同尺寸边坡地形水平和竖向地震动反应谱特性作了研究,并给出岩质坡地斜坡段设计水平地震动放大系数;文献[8]研究了弹性层状半空间凸起地形SH波入射下地震放大作用,表明土层动力特性对凸起地形地震动特性有很大影响.上述研究主要集中在有限尺寸地形对地震动放大的探讨,对不同尺寸凸起地形对地震动放大效应规律的研究还相当少.
为此,本文设计了不同尺寸凸起地形模型,其中包括坡角度在30~60°,凸起高度20~80 m和平台段宽度50~600 m共60个不同尺寸地形,引入动态子结构法进行计算,以分析不同尺寸凸起地形在地震动输入下的响应规律,为实际工程中山地建筑地震动设计提供参考.
1 动态子结构法求解过程建立整体模型,并形成各子结构分析模型,对子结构形成原始边界条件并提取各子结构主模态及对应的刚度和质量矩阵.将主模态刚度矩阵,质量矩阵进行分块处理,通过基于势能的截断准则截取主模态的前k阶,以形成主模态矩阵
| $ {\mathit{\boldsymbol{\emptyset }} _{\rm{c}}} = - \mathit{\boldsymbol{K}}_{{\rm{Ⅱ}}}^{ - 1}{\mathit{\boldsymbol{K}}_{{\rm{IB}}}} $ | (1) |
式中:KⅡ和KIB分别是子结构刚度矩阵和子矩阵,下标Ⅰ表示子结构内部节点,B表示边界节点.
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}^{\rm{I}}}}\\ {{\mathit{\boldsymbol{u}}^{\rm{B}}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}}} \end{array}} \right] \left[{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_k}}\\ {{\mathit{\boldsymbol{u}}^{\rm{B}}}} \end{array}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\emptyset}}_k}}&{{\mathit{\boldsymbol{\emptyset}}_{\rm{c}}}}\\ \mathit{\boldsymbol{0}}&\mathit{\boldsymbol{I}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{q}}_k}}\\ {{\mathit{\boldsymbol{u}}^{\rm{B}}}} \end{array}} \right\} = \mathit{\boldsymbol{T}} \cdot \mathit{\boldsymbol{q}}\mathit{\boldsymbol{.}} $ | (2) |
子结构物理运动方程左乘以T的转置得到子结构广义运动方程式(3),并通过式(4)和式(5)求子结构的广义刚度和质量矩阵[K]和[M].
| $ [\overline{\mathit{\boldsymbol{M}}}]\{\mathit{\boldsymbol{\ddot{q}}}\}+[\overline{\mathit{\boldsymbol{C}}}]\{\overset{\mathit{\boldsymbol{.}}}{\mathop{\mathit{\boldsymbol{q}}}}\,\}+\mathit{\boldsymbol{ }}\!\![\!\!\text{ }\overline{\mathit{\boldsymbol{K}}}]\{\mathit{\boldsymbol{q}}\}=\bar{F}(t), $ | (3) |
式中:
| $ \begin{array}{l} [\mathit{\boldsymbol{\overline K}} ] = {[\mathit{\boldsymbol{T}}]^{\rm{T}}}[\mathit{\boldsymbol{K}}][\mathit{\boldsymbol{T}}] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}&0\\ 0&{{\mathit{\boldsymbol{K}}_{{\rm{BB}}}} + {\mathit{\boldsymbol{K}}_{{\rm{BI}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_k}}&0\\ 0&{{{\mathit{\boldsymbol{\overline K}} }_{{\rm{BB}}}}} \end{array}} \right]. \end{array} $ | (4) |
| $ [\mathit{\boldsymbol{\bar M}}] = {[\mathit{\boldsymbol{T}}]^{\rm{T}}}[\mathit{\boldsymbol{M}}][\mathit{\boldsymbol{T}}] = \\\;\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}\\ {\left( {{\mathit{\boldsymbol{M}}_{{\rm{BI}}}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}{\mathit{\boldsymbol{M}}_{{\rm{II}}}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}} \end{array}} \right.\left. {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k^{\rm{T}}\left( {{\mathit{\boldsymbol{M}}_{{\rm{II}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}} + {\mathit{\boldsymbol{M}}_{{\rm{IB}}}}} \right)}\\ {{\mathit{\boldsymbol{M}}_{{\rm{BB}}}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{M}}_{{\rm{II}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{M}}_{{\rm{IB}}}} + {\mathit{\boldsymbol{M}}_{{\rm{BI}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{c}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&{{{\mathit{\boldsymbol{\bar M}}}_{{\rm{te}}}}}\\ {{{\mathit{\boldsymbol{\bar M}}}_{{\rm{Bl}}}}}&{{{\mathit{\boldsymbol{\bar M}}}_{{\rm{BB}}}}} \end{array}} \right]. $ | (5) |
根据对接边界上的位移协调式(6)和力的平衡条件式(7),再按照“对号入座”的装配方式,将子结构广义坐标下的运动方程进行合并组装,形成整体体系运动方程式(8).
| $ u_1^{\rm{B}} = u_2^{\rm{B}}, $ | (6) |
| $ f_1^{\rm{B}} + f_2^{\rm{B}} = 0, $ | (7) |
| $ [\mathit{\boldsymbol{\tilde{M}}}]\{\mathit{\boldsymbol{\ddot{q}}}\}+[\mathit{\boldsymbol{\tilde{C}}}]\{\overset{\mathit{\boldsymbol{.}}}{\mathop{\mathit{\boldsymbol{q}}}}\,\}+[\widetilde{\mathit{\boldsymbol{K}}}]\{\mathit{\boldsymbol{q}}\}=\tilde{F}(t). $ | (8) |
式中:
为验证动态子结构法在大型有限元计算中的正确性,采用整体法和shake91进行验算并与动态子结构法结果进行对比(仅考虑线弹性分析)[9-10].
验算模型尺寸为:土体宽度L=5 000 m,深度H=400 m,边界为自由边界.其子结构划分为A、B、C、D四个子结构,具体划分情况为:子结构A尺寸为5 000 m×200 m,子结构B和D均为1 500 m×200 m,子结构C为2 000 m×200 m,详细划分见图 1.

|
图 1 验算模型 Fig. 1 Checking model |
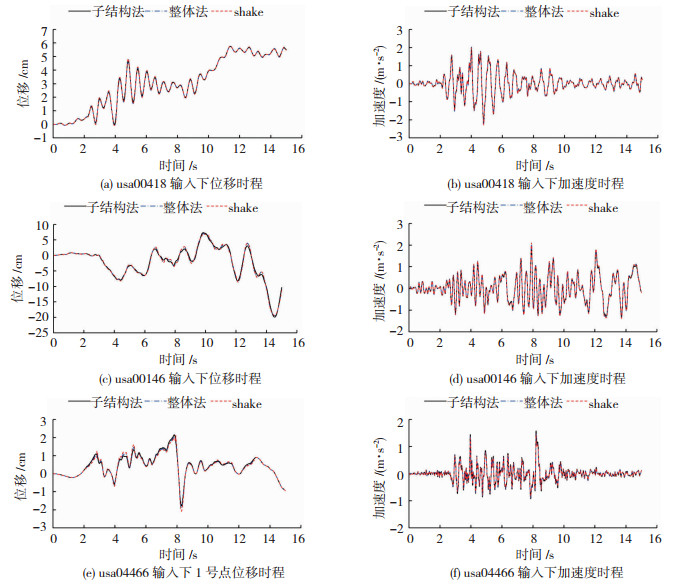
土体为基岩,弹性模量E=1.323×1010 N/m2,泊松比ν=0.25,密度ρ=2 700 kg/m3,SV波波速为Cs=2 425 m/s,材料阻尼比ξ=0.05,网格划分为10 m,地震波输入同为岩石基站采集的天然波3条Usa00418、Usa00146和Usa04466,其分别对应的峰值加速度为143.51、147.1、102.47 cm/s2.由岩层底部输入地震波,采集平地1号点位移及加速度响应时程,计算结果见图 2.其中,以shake计算结果为准,有限元计算整体法和子结构法计算结果及误差见表 1.
|
图 2 1号点位移和加速度对比 Fig. 2 Displacement and acceleration contrast diagram of point 1 |
| 表 1 不同方法计算结果对比 Tab. 1 Calculation results of different methods |
由表 1可知,与shake计算结果做对比,自由边界整体有限元计算结果位移和加速度最大值误差均在1.2%以内,子结构法误差均在2.5%以内.相比与传统有限元法,子结构法可在保证计算精度的同时大幅提高计算效率.
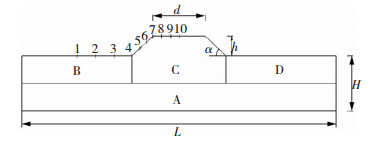
3 不同尺寸凸起地形对地震响应影响规律分析 3.1 计算模型参数及地震波选取土体边界采用自由场边界,为保证计算精度,土体宽度L=5 000 m,土体高度H为400 m,台地高度分别取h=20、40、60、80 m,边坡角度考虑α=30°、45°、60°三种情况,坡顶平台段宽度分别取d=50、100、200、400、600 m(经过大量计算所得,平台宽度d与高度h比值大于8,平台宽度对地震动放大的影响程度很小,故本文平台最大宽度d取600 m),由于凸起平台左右对称,故采样点仅考虑左半模型,具体为下平台段3个点,坡脚坡顶各一个点,斜坡上2个点,坡顶平台3个点共计10个点.具体模型及子结构划分情况见图 3(子结构详细尺寸同第2节).
|
图 3 计算简图 Fig. 3 Calculation diagram |
场地土质为岩质坡地,模型的物理参数取值同第2节.模型有限元参数取值为:单元网格尺寸应为1/10~1/8个感兴趣的最小波长,由于计算模型感兴趣频率均为0.1~15 Hz,故本文拟选用频段为0.1~20 Hz的白噪声进行激励,对应的最小波长为120 m左右,故网格大小可选择12 m.有限元计算时间间隔一般为Δt=1/10×fmax,本文计算最大频率为20 Hz,故时间间隔取Δt=0.002 s,本模型阻尼采用瑞雷阻尼,为忽略阻尼对地形的影响,故模型阻尼系数均取δ=0,β=0.000 1.为反映地震动增大的真实情况,本文随机选用峰值加速度为320 cm/s2,持续时间为20 s的20条白噪声,取计算平均数作为最后分析结果.
3.2 不同尺寸凸起地形对PGA的影响规律分析通过动态子结构法的计算,求得各模型各观测点最大加速度比值(其他观测点均以1号点为基准点,除以1号观测点加速度得到加速度增大系数),分析时域内不同尺寸凸起地形对地震动放大的影响.
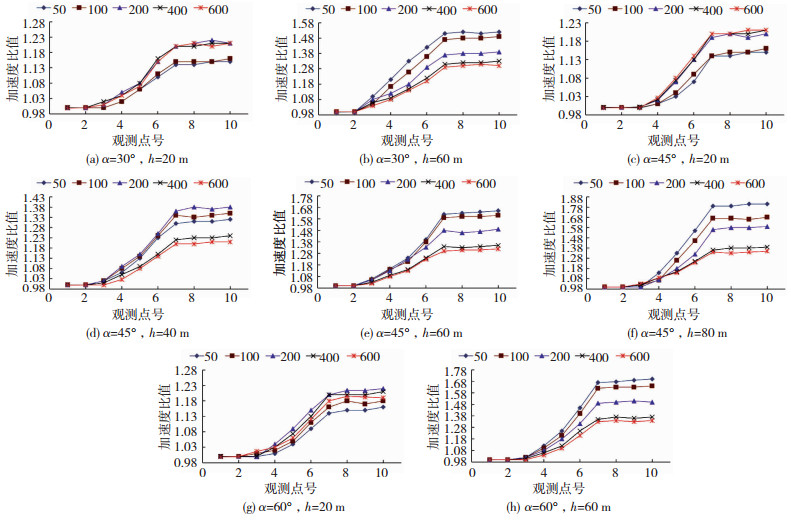
由于文章篇幅有限,仅给出α30h20、α30h60、α45h60和α60h60四种情况加速度比值(其中α表示坡角度值,h表示平台凸起高度值),具体结果见图 4(图中50、100、200、400、600表示平台宽度d=50、100、200、400、600 m).
|
图 4 各点不同尺寸地形最大加速度比值 Fig. 4 Maximum acceleration ratio of different-size terrains at each point |
由图 4可知,从1号点到10号点,各计算模型最大加速度比值均有增加趋势,不同尺寸凸起地形对加速度变化规律有一定影响,平台宽度不变情况下,加速度随坡角度和凸起高度的增大而增大,但加速度随坡角度变化的增大幅度很小,凸起高度的变化对加速度增大程度影响很大.
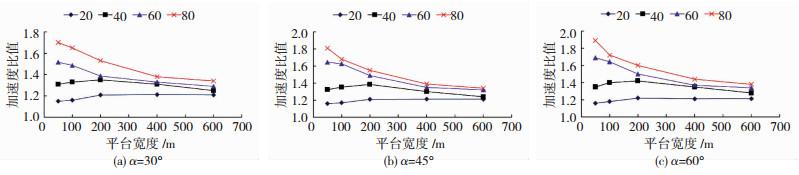
从各观测点加速度增大程度来看,同等条件下,由于平台中点受到斜坡面地震动反射叠加效果最为明显,故凸起地形坡顶平台中点(10号点)增加趋势最明显,平台中点(10号点)的加速度在不同尺寸地形下的变化情况见图 5(图中20、40、60、80表示平台高度h=20、40、60、80 m).
|
图 5 平台中点(10号点)不同平台宽度最大加速度放大系数 Fig. 5 Maximum acceleration variation curves of the midpoints (point 10) of platforms with different widths |
由图 5可知,平台宽度的变化对不同尺寸凸起地形加速度放大规律有较大影响.当凸起高度很小时(h=20、40 m),加速度增大值随平台宽度的增大呈先增大后略微减小的趋势,且整体变化程度不大;当凸起地形尺寸变大,凸起高度为h=40、60 m时,加速度增大值随平台宽度的增大呈减小趋势,且减小趋势明显.不同模型中最大加速度减小百分率见表 2(此百分率为平台宽度为50 m和600 m时的10号点最大加速度减小值),凸起高度越高,随平台宽度的增加各点最大加速度减小幅度越明显.
| 表 2 10号点最大加速度减小百分率 Tab. 2 Percentage reduction of maximum acceleration at point 10 |
计算了不同高度不同角度和不同平台宽度下各模型的加速度反应谱,并用其他各观测点反应谱除以1号观测点反应谱得到谱比值,分析频域内不同观测点地震动放大效应.本节内容提取具有代表性的部分模型结果进行规律分析,图 6给出了坡角度α=30°,高度h=60 m,平台宽度d=200 m各观测点的谱比值(其它模型规律相似).
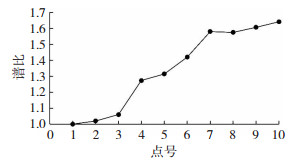
由图 6可知,各点最大谱比值变化规律与加速度最大比值变化规律一致,地震动放大效应随点号的增大呈增大趋势,对于斜坡段,坡顶的谱比值高于其他斜坡点,在坡顶平台段,平台中心(10号点)谱比值最大,其他平台点谱比随离平台中心的距离增加呈略微减小趋势,故以下均以10号点分析结果(其他点规律相似)作为研究对象,分析频域内不同尺寸凸起地形对坡顶地震动放大程度的影响.10号点不同凸起地形尺寸下加速度反应谱计算结果见图 7(图中50、100、200、400、600表示平台宽度为d=50、100、200、400、600 m).
|
图 6 各点谱比值曲线 Fig. 6 Spectral ratio curve of each point |
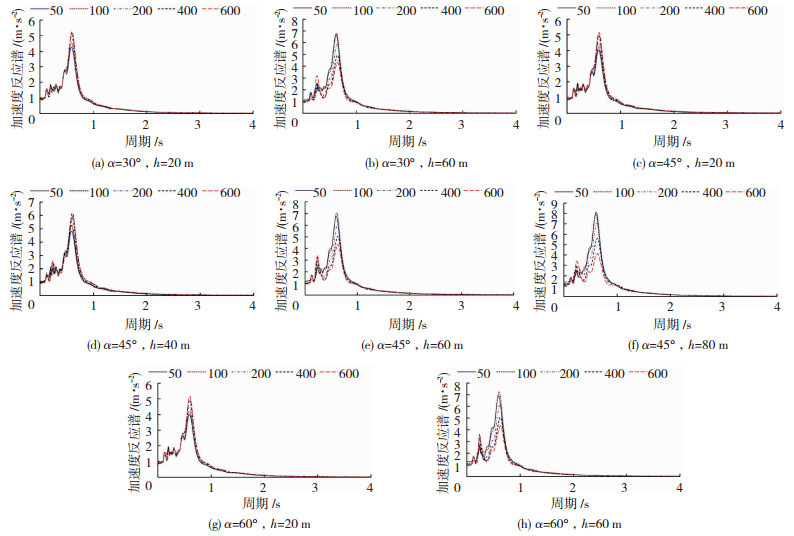
由图 7可知,反应谱最大值随坡角度和高度的增加呈增加趋势,且凸起地形尺寸的大小对反应谱形状有很大影响.随地形尺寸增大(高度和宽度增加),地形尺寸效应凸显,地形高频段(周期为0.2 s左右)反应渐渐增大并呈现双峰,且第二峰值(0.7 s左右)逐渐减小.说明地形尺寸的增大会使得高频段振动加强,低频段响应相对减弱,此结论与李英民等[7]计算规律相似.为分析各模型反应谱增大程度,10号点不同尺寸凸起地形反应谱最大值变化曲线见图 8(图中20、40、60、80表示平台高度h=20、40、60、80 m).
|
图 7 10号点不同模型反应谱曲线 Fig. 7 Spectral curves of different models at point 10 |

|
图 8 10号点不同模型反应谱最大值 Fig. 8 Maximum response spectra of different models at point 10 |
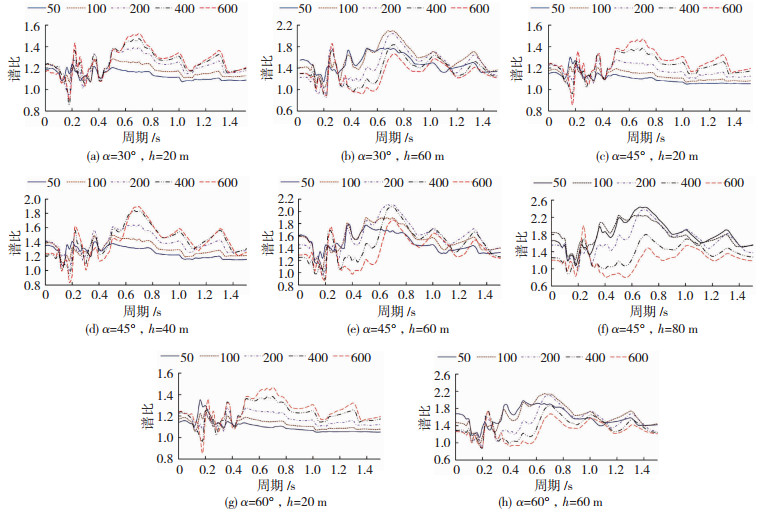
由图 8可知,规律与加速度结果类似,地形尺寸相对较小时,凸起地形地震动响应随平台宽度的增加呈先增加后减小趋势,且变化幅度很小;地形尺寸较大时,地震动响应随平台宽度增加而减小.不同尺寸模型10号点谱比曲线见图 9(图中50、100、200、400、600表示平台宽度d=50、100、200、400、600 m).
|
图 9 10号点不同模型谱比曲线 Fig. 9 Spectral ratio curves of different models at point 10 |
由图 9可知:1)谱比值随着坡角的增加和坡高度增加呈增大趋势,且随地形的宽度和高度的变化,谱比峰值频段出现明显变化;2)当地形凸起尺寸相对较小时(h=20、40 m),由于局部地形过于平坦,地形本身对地震动的放大效应整体不太明显.此时随着凸起地形宽度增加,受长周期地震动影响比较明显,其在周期为0.8 s左右的低频段谱比值显著增加;3)当地形凸起尺寸相对较大时(h=60、80 m),地形尺寸效应开始凸显,地形对地震动高频段响应变得敏感,此时随着凸起地形宽度的增加,谱比在周期为0.2 s左右高频段呈增加趋势,而在周期为0.8 s左右的低频段呈明显降低趋势.由此可知凸起地形尺寸的增加会增大地震动高频阶段响应,减小低频段响应,在凸起高度达到一定高度时,地形放大效应随平台宽度的增加总体呈减小趋势,此结论与郝明辉等[5]计算规律相似.
4 结论1) 动态子结构法在保证大型有限元模型计算精度的同时,能够有效提高计算效率.
2) 不同尺寸凸起地形对地震加速度响应有很大影响.相同尺寸地形下,在斜坡段,从坡角到坡顶加速度呈增大趋势,坡顶平台段中心点加速度最大;且随地形坡角和高度的增加,各点加速度均呈增加趋势.
3) 地形宽度变化对加速度放大的影响相对复杂,在地形高度达到一定程度时,凸起地形各点加速度随坡顶宽度增加而减小,且凸起尺寸高度越高减小幅度越大;反之,各点加速度呈小幅增加趋势.
4) 不同尺寸凸起地形对反应谱和谱比影响趋势与加速度响应规律相近.不同之处在于,地形凸起高度的增加会激发高频段反应的加剧,同时降低低频段反应峰值.
| [1] |
刘洪兵, 朱稀. 地震中地形放大效应的观测和研究进展[J]. 世界地震工程, 1999, 15(3): 20. LIU Hongbing, ZHU Xi. Advance on topographic amplification effects of seismic response[J]. World Earthquake Engineering, 1999, 15(3): 20. |
| [2] |
荣棉水, 李小军. 局部地形对出平面运动谱特性的影响分析[J]. 中国地震, 2007, 23(2): 147. RONG Mianshui, LI Xiaojun. The effect analysis of topography on the spectrum property of anti-plane movement[J]. Earthquake Research in China, 2007, 23(2): 147. DOI:10.3969/j.issn.1001-4683.2007.02.005 |
| [3] |
荣棉水, 李小军, 吕悦军. 平台地形地面运动特征周期值的影响[J]. 中国地震, 2009, 25(2): 178. RONG Mianshui, LI Xiaojun, LU Yuejun. Effect of protruding topography on characteristic period of ground motion[J]. Earthquake Research in China, 2009, 25(2): 178. DOI:10.3969/j.issn.1001-4683.2009.02.008 |
| [4] |
刘晶波. 局部不规则地形对地震地面运动的影响[J]. 地震学报, 1996, 18(2): 239. LIU Jingbo. Influence of local irregular topography on seismic ground motion[J]. Acta Seismologica Sinica, 1996, 18(2): 239. |
| [5] |
郝明辉, 张郁山. 凸起地形对地震动特性的影响[J]. 地震学报, 2014, 36(5): 883. HAO Minghui, ZHANG Yushan. Analysis of terrain effect on the properties of ground motion[J]. Acta Seismologica Sinica, 2014, 36(5): 883. |
| [6] |
GEORGE D, ACHILLEAS G. Numerical evaluation of slope topography effects on seismic ground motion[J]. Soil Dynamics and Earthquake Engineering, 2005, 25: 547. DOI:10.1016/j.soildyn.2004.11.008 |
| [7] |
李英民, 王丽萍, 赵耀. 岩质坡地建筑设计水平地震动放大系数的确定[J]. 地震工程与工程振动, 2010, 30(4): 159. LI Yingmin, WANG Liping, ZHAO Yao. Amplification factors of design horizontal ground motions for structures on rock slops[J]. Earthquake Engineering and Engineering Dynamics, 2010, 30(4): 159. |
| [8] |
梁建文, 巴振宁. 弹性层状半空间中凸起地形对入射平面SH波的放大作用[J]. 地震工程与工程振动, 2008, 28(1): 1. LIANG Jianwen, BA Zhenning. Surface motion of a hill in layered half-space subjected to incident plane SH waves[J]. Earthquake Engineering and Engineering Dynamics, 2008, 28(1): 1. |
| [9] |
GE Z X, CHEN X F. An efficient approach for simulating wave propagation with the boundary element method in multilayered media with irregular interfaces[J]. Bulletin of the Seismological Society of America, 2008, 98(6): 3007. DOI:10.1785/0120080920 |
| [10] |
ZHANG W, CHEN X F. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophysical Journal International, 2006, 7(1): 337. |
 2019, Vol. 51
2019, Vol. 51


