隔震结构体系具有较好的隔震性能,近年来在高烈度地区的建筑结构中得到了广泛应用[1].采用叠层橡胶支座的隔震结构体系由上部结构与隔震支座组成,支座水平刚度较小.水平地震作用下,通过延长结构周期减小上部结构受到的地震力.而在竖向地震及自重作用下,由于支座竖向刚度较大,能够有效保证隔震结构稳定性.
由于橡胶支座水平刚度随剪切变形增加而不断减小,分析时需要根据地震作用(大震或小震)输入不同剪切程度下的支座水平刚度,而支座竖向刚度不随竖向位移变化,计算时常取初始竖向刚度.而研究表明,地震作用下,支座竖向刚度随剪切变形增加发生显著退化,目前结构设计软件及设计规范均未考虑此现象,会对上部结构及支座自身安全造成一定影响,需进一步研究[2].近年来,国内外学者对叠层橡胶支座的竖向力学性能进行了研究,根据支座双弹簧模型及有效面积模型,推导了支座压缩刚度[2]及拉伸刚度[3]退化公式,或通过试验对支座偏压[4]及偏拉[5]性能进行研究,总结剪切变形状态下支座刚度退化规律.已有研究表明,支座竖向刚度退化会对隔震系统自身及周围构件产生不利影响[6],然而其对整体结构的影响研究较少.罕遇地震作用下,支座产生较大剪切变形,竖向刚度退化效应明显,有必要分析支座竖向刚度退化对整体隔震结构产生的不利影响,保证结构安全.
为此,首先根据中国现行规范设计了不同层数、层高、柱距的钢筋混凝土隔震框架结构;然后通过ABAQUS软件建立整体结构有限元模型,考虑上部结构在罕遇地震作用下进入塑性;隔震支座采用修正的双弹簧模型刚度退化结果,利用用户单元子程序(UEL)自定义支座单元,采用FORTRAN语言二次开发能够考虑支座竖向刚度退化的程序;通过输入实际地震记录对结构进行弹塑性动力时程分析,计算整体隔震结构变形及受力,研究支座竖向刚度退化对结构地震响应的影响,提出考虑支座竖向刚度退化的上部结构地震响应放大系数,为今后进行罕遇地震作用下隔震结构计算分析提供重要依据.
1 隔震结构设计为研究支座发生剪切变形后竖向刚度退化对不同参数框架结构地震响应的影响,以5层钢筋混凝土框架结构为基本模型,在此基础上分别改变结构层高、层数及柱距参数并进行隔震结构设计,平面与立面布置见图 1,模型参数见表 1.设定结构所在地区抗震设防烈度为8度(0.2g),Ⅱ类场地,设计分组第1组,设防类别丙类.

|
图 1 结构平立面布置 Fig. 1 Structural plane and vertical layout |
| 表 1 各模型参数 Tab. 1 Parameters of the models |
混凝土采用C30,纵筋及箍筋均采用HRB335,按照中国规范进行截面设计.假定结构顶层恒载6.0 kN/m2,活载2.0 kN/m2,其余层恒载5.0 kN/m2,活载2.0 kN/m2,梁间荷载4.0 kN/m2[7].有限元计算时,将作用在平面框架结构上的恒载及活载转化为重力荷载代表值进行分析.
通过SAP2000软件建立上部结构进行隔震设计,柱底隔震层选取叠层橡胶支座,支座参数见表 2,满足《建筑抗震设计规范》[8]中丙类建筑支座压应力限值要求.通过弹性时程分析,得到结构水平向减震系数小于0.4,按照规范要求,上部结构可降低1度设计.考虑到结构罕遇地震下的安全性,PKPM中对上部结构降低半度,即7度(0.15g)进行内力计算及配筋设计[7].
| 表 2 橡胶支座参数 Tab. 2 Parameters of the rubber bearings |
根据结构尺寸及配筋结果,通过ABAQUS有限元软件建立整体隔震结构模型,上部结构选用纤维模型.由于在大震作用下上部结构可能进入塑性产生损伤退化,混凝土材料采用损伤塑性本构模型,受压骨架曲线选取Scott[9]修正的Kent-Park模型,受拉段采用Yassin[10]提出的加卸载准则,本构模型示意见图 2.为反映结构各构件真实强度,采用材料平均强度进行计算[11].为考虑箍筋对混凝土的约束效应,引入材料峰值应力应变强化因子K.钢材采用提出的双折线强化模型[12],可有效模拟钢材滞回曲线在循环荷载作用下产生的捏拢效应.C30混凝土及HRB335材料参数见表 3、4.
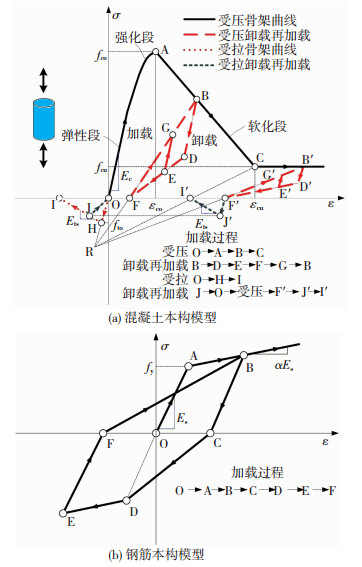
|
图 2 混凝土及钢筋本构模型 Fig. 2 Constitutive models of the concrete and the rebar |
| 表 3 混凝土参数 Tab. 3 Parameters of the concrete |
| 表 4 钢筋参数 Tab. 4 Parameters of the rebar |
表 3中,fco为受压峰值应力,εco为受压峰值应变,fcu为极限压应力,εcu为极限压应变,λ为达到极限压应变时卸载刚度与初始弹性模量之比,fto为受拉峰值应力,Ets为受拉软化模量.表 4中,Es为弹性模量,fy为屈服强度,α为塑性刚度系数.
梁柱采用ABAQUS三维纤维梁单元B31模拟,根据纤维单元计算要求,在梁长方向划分10个单元[13],在INP文件中增加截面积分点,并通过“*rebar”命令添加钢筋纤维.楼板采用四节点分层壳单元S4R模拟,板中钢筋通过“rebar layers”命令添加,并沿板厚方向添加相应积分点数量,构件截面纤维布置见图 3.
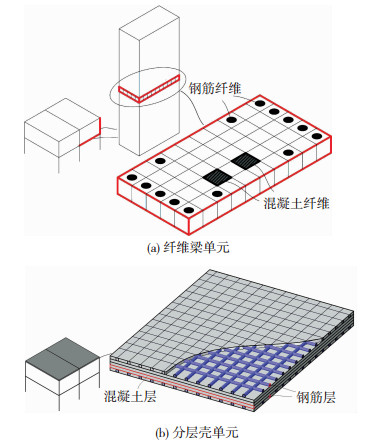
|
图 3 纤维梁与分层壳单元截面 Fig. 3 Sections of the fiber beam and the layered shell element |
由于支座竖向刚度与剪切变形相互耦联,竖向刚度随剪切变形增加而退化,当支座顶部剪切变形达到规范限值时,竖向刚度退化为初始刚度的50%左右[14],而目前常用结构设计软件及有限元分析软件所提供的支座单元均无法模拟此现象.为此,根据修正后双弹簧模型竖向刚度退化结果[15],采用ABAQUS用户单元子程序(UEL)接口,利用FORTRAN语言二次开发了能有效模拟支座竖向本构关系的支座单元,其竖向控制方程为
| $ {{F}_{\rm{v}}}={{K}_{\rm{v}}}v, $ | (1) |
式中:Fv为单元竖向轴力,v为轴向变形,Kv为竖向刚度,可由式(2)得到
| $ {{K}_{\rm{v}}}=\frac{{{K}_{\rm{vo}}}}{1+\frac{2.30{{u}^{2}}}{{{\pi }^{2}}R_{\rm{i}}^{2}}}, $ | (2) |
式中:u为单元两端节点相对水平位移,Ri为支座截面惯性半径,Kvo为支座初始刚度,可由式(3)~(5)计算得到[16]:
| $ {{K}_{\rm{vo}}}=\frac{{{E}_{\rm{c}}}A}{{{n}_{\rm{r}}}{{t}_{\rm{r}}}}, $ | (3) |
| $ {E_{\rm{c}}} = {\left[ {\frac{1}{{{E_{{\rm{ap}}}}}} + \frac{1}{{{E_\infty }}}} \right]^{ - 1}}, $ | (4) |
| $ {E_{{\rm{ap}}}} = {E_{\rm{o}}}\left( {1 + 2\kappa S_1^2} \right). $ | (5) |
式中:A为支座截面面积,Eap及E∞分别为橡胶表观模量及体积模量,κ为弹性模量修正系数.
建立隔震结构整体模型时,支座单元一端节点与柱脚合并,另一端节点固定.支座单元程序开发流程见图 4,程序开始计算时,将隔震支座参数传入UEL子程序,UEL根据传入参数更新状态变量并返回整体结构中,实现支座竖向刚度随单元节点位移变化而改变.
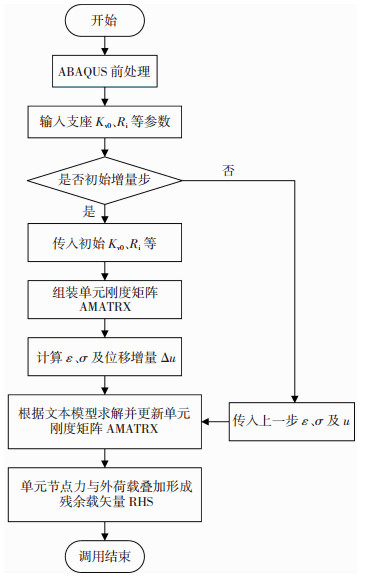
|
图 4 支座单元程序开发流程 Fig. 4 Program development flow of the bearing element |
选取文献[17]中剪切变形下叠层橡胶支座压缩试验与文献[18]中拉伸试验进行验证,支座参数见表 5.通过ABAQUS建立考虑刚度退化的UEL单元,同时与ABAQUS单元库中自带的模拟支座的弹簧单元进行对比.
| 表 5 文献支座参数 Tab. 5 Parameters of the bearings in literatures |
支座单元竖向刚度退化数值分析与试验结果对比见图 5.由图可知,采用考虑支座刚度退化的支座UEL单元计算结果能够有效模拟出支座在剪切变形作用下的刚度退化现象,与试验结果吻合良好;而ABAQUS自带支座单元为线性单元,竖向刚度不随剪应变增加发生变化.根据二者对比结果,在整体隔震结构地震响应分析中需采用二次开发的支座单元.
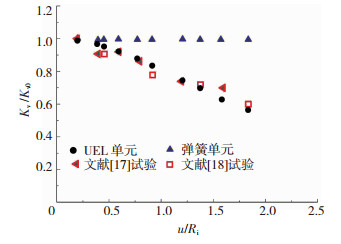
|
图 5 自定义单元试验验证 Fig. 5 Experimental verification of the user defined element |
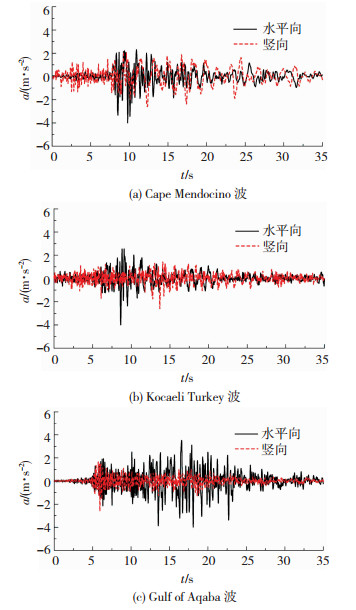
根据目标反应谱选波原则,通过太平洋地震工程研究中心(PEER)数据库选取实际强震记录,震级为7~8度,地震动选取结果见表 6.将所选地震波生成对应的地震反应谱,与抗震设计规范目标反应谱进行对比,见图 6.由图可知二者拟合度较好,选波合理.分析时地震波根据规范进行调幅,调幅后地震波时程曲线见图 7,水平与竖向峰值加速度分别为0.4 g、0.26 g.
| 表 6 地震波记录 Tab. 6 Ground motion records |

|
图 6 地震波反应谱与目标谱对比 Fig. 6 Comparison of earthquake response spectrums and target spectrum |
|
图 7 地震波加速度时程曲线 Fig. 7 Acceleration time-history curves of earthquakes |
隔震结构中,竖向地震可能导致支座拉压应力过大发生破坏,或由于P-Δ效应显著而发生屈曲.因此,在隔震结构动力响应分析时应考虑竖向地震对结构的作用.对整体隔震结构进行弹塑性动力时程分析,首先将重力荷载代表值转化为重力荷载施加于上部结构,然后同时在结构水平及竖向输入地震加速度时程.模型分析工况见表 7,对比分析罕遇地震下考虑支座刚度退化前后对上部结构构件变形及受力响应的影响.
| 表 7 模型分析工况 Tab. 7 Analysis conditions of the models |
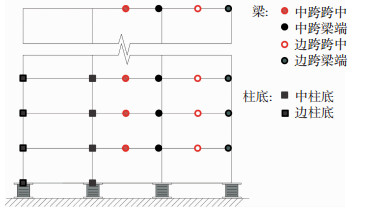
提取结果主要有6个,分别为:考虑支座竖向刚度退化前后柱底剪力、轴力及弯矩,各层梁跨中及梁端弯矩,支座顶部剪切变形,层间位移.模型中梁柱响应提取点见图 8.
|
图 8 计算结果提取点 Fig. 8 Extraction points of the calculation results |
通过ABAQUS计算得到结构前3阶周期见表 8,隔震结构基本周期达到非隔震基本周期3倍以上,隔震效果显著.隔震后上部结构振型由剪切型变为整体平动型.以模型F5为例,模态分析基本振型隔震前后变化见图 9.
| 表 8 模态分析结果 Tab. 8 Modal analysis results |

|
图 9 F5模型1阶振型 Fig. 9 First mode shape of model F5 |
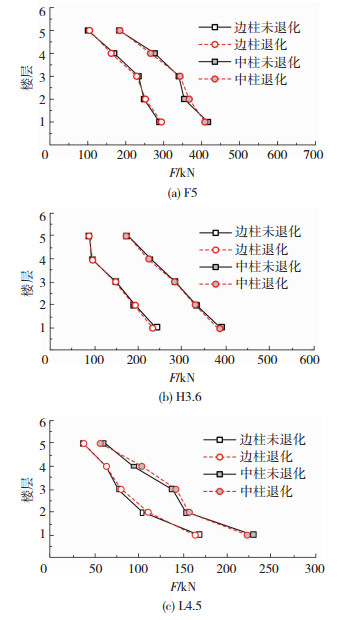
图 10是以F5、H3.6、L4.5这3个模型为例,地震波GA作用下各层中柱及边柱柱底剪力对比情况,综合GA、CM、KT这3条地震波及不同层数、层高、柱距模型计算结果可得:支座竖向刚度退化对各层剪力幅值影响并不相同.考虑刚度退化后,不同参数模型各层柱底剪力幅值变化范围为-11.9%~14.9%,需考虑总体影响.若不考虑支座刚度退化将低估某些工况下的柱底剪力,使结构偏于不安全.在大震弹塑性分析,可将未考虑支座竖向刚度退化模型计算结果乘以剪力放大系数1.15.
|
图 10 3个模型工况G-NO与G-DE下各层柱底剪力对比 Fig. 10 Comparison of shear force at the bottom of column between conditions G-NO and G-DE of 3 models |
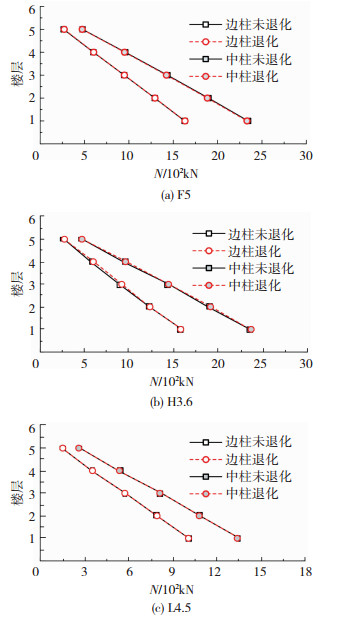
图 11是以F5、H3.6、L4.5这3个模型为例,地震波GA作用下柱底轴力对比情况,同理综合所有模型计算结果可得:考虑支座竖向刚度退化后,边柱及中柱最大轴力均有不同程度增加,最大增幅分别约为6.0%、5.6%.取最大增幅包络值进行分析,不同参数模型中,可将未考虑支座竖向刚度退化柱底轴力计算值,在中柱位置乘以轴力放大系数1.1.
|
图 11 3个模型工况G-NO与G-DE下各层柱底轴力对比 Fig. 11 Comparison of axial force at the bottom of column between conditions G-NO and G-DE of 3 models |
图 12是以F5、H3.6、L4.5这3个模型为例,GA波作用下各层柱底弯矩对比情况,综合所有模型计算结果可得:支座竖向刚度退化对各层柱底弯矩的影响并不统一,考虑刚度退化后,边柱与中柱柱底弯矩最大增幅分别为9.5%、11.9%,某些楼层中,柱底弯矩有所减小,为简化考虑支座竖向刚度退化影响,可将边柱与中柱柱底弯矩分别放大1.1倍、1.15倍.
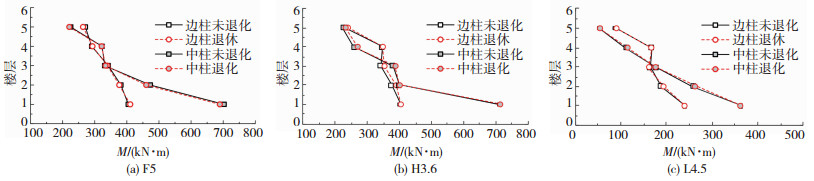
|
图 12 3个模型工况G-NO与G-DE各层柱底弯矩对比 Fig. 12 Comparison of bending moment at the bottom of column between conditions G-NO and G-DE of 3 models |
图 13是以F5、H3.6、L4.5这3个模型为例,GA波作用下模型各层梁跨中与梁端弯矩值,综合所有模型计算结果可得:对于不同参数模型,支座竖向刚度对梁跨中与梁端弯矩影响均较大,考虑支座刚度退化最大可使梁跨中与梁端弯矩分别增加28.8%、12.1%,因此分析竖向刚度退化对梁弯矩影响时,可将梁弯矩值放大1.3倍.
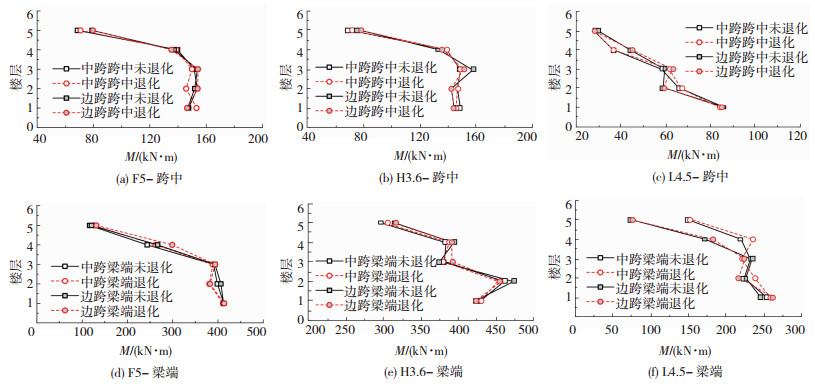
|
图 13 3个模型工况G-NO与G-DE各层梁弯矩对比 Fig. 13 Comparison of bending moment of beam between conditions G-NO and G-DE of 3 models |
图 14是以F5、H3.6、L4.5这3个模型为例,GA波作用下支座顶部剪切变形时程变化曲线,综合所有模型计算结果可得:对于不同参数模型,考虑支座刚度退化后剪切变形均基本不变,最大增幅约为2.4%,支座竖向刚度退化对剪切变形影响较小.

|
图 14 3个模型工况G-NO与G-DE支座顶剪切变形对比 Fig. 14 Comparison of shear deformation at the top of bearings between conditions G-NO and G-DE of 3 models |
图 15是以F5、H3.6、L4.5这3个模型为例,GA波作用下支座竖向刚度退化前后上部结构层间位移变化情况,综合GA、CM、KT这3条地震波作用下所有模型计算结果可得:对于不同参数模型,结构层间位移基本一致,最大增幅约0.11%,故支座竖向刚度退化对楼层层间位移影响较小.
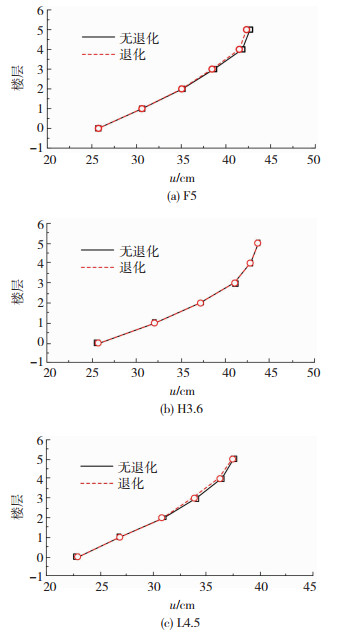
|
图 15 3个模型工况G-NO与G-DE结构层间位移对比 Fig. 15 Comparison of interlayer displacement of structures between conditions G-NO and G-DE of 3 models |
综合不同层数、层高、柱距框架结构各模型计算结果可知,地震作用下支座竖向刚度退化对柱底剪力、轴力、弯矩及梁弯矩响应均有一定影响,对支座顶部剪切变形及上部结构层间位移无显著影响.最终可得到考虑支座竖向刚度退化影响的放大系数见表 9.
| 表 9 地震响应放大系数 Tab. 9 Seismic response amplification factors |
1) 根据支座竖向刚度退化理论公式,在ABAQUS中二次开发了能够考虑竖向刚度退化的叠层橡胶支座单元,通过对比试验结果,验证了所开发支座单元程序有效性,实现了利用杆系单元模拟支座竖向刚度退化现象.
2) 对于Ⅱ类场地,支座竖向刚度退化对结构柱底剪力、柱底轴力与梁弯矩有一定影响,对于未考虑支座竖向刚度退化模型结果,可分别取地震响应放大系数1.15、1.1及1.3.支座竖向刚度退化对结构不同位置柱底弯矩影响不同,边柱及中柱可分别取地震响应放大系数1.1及1.15.
3) 对于所分析的不同参数结构模型,支座竖向刚度退化对支座剪切变形及上部结构层间位移影响较小,可不考虑支座竖向刚度退化对二者的影响.
| [1] |
国巍, 余志武, 柳国环, 等. 大跨隔震结构多点地震计算模型的几点注记[J]. 哈尔滨工业大学学报, 2013, 45(10): 87. GUO Wei, YU Zhiwu, LIU Guohuan, et al. Notes about calculation models for seismic analysis of long-spanisolated structure under multi-point earthquake excitations[J]. Journal of Harbin Institute of Technology, 2013, 45(10): 87. |
| [2] |
WARN G P, WHITTAKER A S, CONSTANTINOU M C. Vertical stiffness of elastomeric and lead-rubber seismic isolation bearings[J]. Journal of Structural Engineering, 2007, 133(9): 1227. DOI:10.1061/(ASCE)0733-9445(2007)133:9(1227) |
| [3] |
闫维明, 张志谦, 陈适才, 等. 橡胶隔震支座拉伸刚度理论模型与分析[J]. 工程力学, 2014, 31(2): 186. YAN Weiming, ZHANG Zhiqian, CHEN Shicai, et al. Modeling and analyzing of tension stiffness for seismic isolated rubber bearings[J]. Engineering Mechanics, 2014, 31(2): 186. DOI:10.6052/j.issn.1000-4750.2012.07.0544 |
| [4] |
LIU W G, HE W F, FENG D M, et al. Vertical stiffness and deformation analysis models of rubber isolators in compression and compression-shear states[J]. Journal of Engineering Mechanics, 2009, 135(9): 945. DOI:10.1061/(ASCE)EM.1943-7889.0000010 |
| [5] |
王栋, 吕西林. 具有抗拉功能的隔震支座力学性能试验研究[J]. 建筑结构学报, 2015, 36(9): 124. WANG Dong, LYU Xilin. Experimental research on mechanical properties of anti-tension isolation bearing[J]. Journal of Building Structures, 2015, 36(9): 124. DOI:10.14006/j.jzjgxb.2015.09.016 |
| [6] |
WARN G P. The coupled horizontal-vertical response of elastomeric and lead-rubber seismic isolation bearings[D]. New York: The State University of New York, 2006
|
| [7] |
叶昆, 张子翔, 朱宏平. 近场地震竖向分量对LRB基础隔震结构地震响应影响分析[J]. 工程力学, 2016, 33(4): 49. YE Kun, ZHANG Zixiang, ZHU Hongping. Influence of near-field vertical ground motions on the seismic of LRB base-isolated structures[J]. Engineering Mechanics, 2016, 33(4): 49. DOI:10.6052/j.issn.1000-4750.2014.04.0315 |
| [8] |
建筑抗震设计规范: GB 50011-2010[S].北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011-2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [9] |
SCOTT B D. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Structural Journal, 1982, 79(1): 13. |
| [10] |
YASSIN M H M. Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[D]. California: University of California, Berkeley, 1994
|
| [11] |
易伟建, 王维一. 近场区竖向地震动对钢筋混凝土框架结构抗震性能的影响[J]. 土木工程学报, 2012, 45(10): 84. YI Weijian, WANG Weiyi. Effect of vertical ground motion on seismic behavior of RC frame in near-fault region[J]. China Civil Engineering Journal, 2012, 45(10): 84. DOI:10.15951/j.tmgcxb.2012.10.014 |
| [12] |
黄金桥.钢结构弹塑性动力学及抗震设计理论研究[D].杭州: 浙江大学, 2005 HUANG Jinqiao. Elastic-plastic dynamics and aseismic design theory of steel structures[D]. Hangzhou: Zhejing University, 2005 |
| [13] |
李华伟.钢管混凝土柱-钢梁环板式节点抗连续倒塌性能研究[D].兰州: 兰州理工大学, 2014 LI Huawei. The Progressive collapse analysis of steel beam to concrete-filled steel tubular column with ringlike plate connections[D]. Lanzhou: Lanzhou University of Technology, 2014 |
| [14] |
孙新阳, 杨维国, 王萌, 等. 剪切变形下橡胶支座压缩刚度比分析研究[J]. 工程力学, 2017, 34(1): 65. SUN Xinyang, YANG Weiguo, WANG Meng, et al. Compression stiffness ratio of rubber bearings under shear deformation[J]. Engineering Mechanics, 2017, 34(1): 65. DOI:10.6052/j.issn.1000-4750.2015.08.0704 |
| [15] |
YANG W G, SUN X Y, WANG M, et al. Vertical stiffness degradation of laminated rubber bearings under lateral deformation[J]. Construction and Building Materials, 2017, 152: 310. DOI:10.1016/j.conbuildmat.2017.07.004 |
| [16] |
橡胶支座第3部分: 建筑隔震橡胶支座: GB 20688.3-2006[S].北京: 中国建筑工业出版社, 2006 Rubber bearings-Part 3: Elastomeric seismic-protection isolators for buildings: GB20688.3-2006[S]. Beijing: China Architecture & Building Press, 2006 |
| [17] |
沈朝勇, 崔杰, 马玉宏, 等. 超低硬度隔震橡胶支座的竖向力学性能研究[J]. 地震工程与工程振动, 2012, 32(5): 136. SHEN Chaoyong, CUI Jie, MA Yuhong, et al. Vertical mechanical property of elastomeric isolators with ultra-low hardness[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(5): 136. DOI:10.13197/j.eeev.2012.05.021 |
| [18] |
刘亚东, 田杰. 橡胶隔震支座拉伸性能试验研究[J]. 建筑科学, 2015, 31(7): 63. LIU Yadong, TIAN Jie. Experimental study on tension property of isolation bearing[J]. Building Science, 2015, 31(7): 63. DOI:10.13614/j.cnki.11-1962/tu.2015.07.012 |
 2019, Vol. 51
2019, Vol. 51


