2. 混凝土及预应力混凝土结构教育部 重点实验室(东南大学), 南京 210096;
3. 风工程与桥梁工程湖南省重点实验室(湖南大学), 长沙 410082
2. Key Lab of Concrete and Prestressed Concrete Structure (Southeast University), Ministry of Education, Nanjing 210096, China;
3. Key Lab for Wind and Bridge Engineering of Hunan Province (Hunan University), Changsha 410082, China
电涡流阻尼器(ECD)作为一种新型耗能减振装置[1],具有无接触、低摩擦,工作原理简单、安装维护方便以及耐久性好等优点.ECD早期主要应用于车辆悬架、汽车制动等机械以及航空航天等领域[2-3],目前在土木工程领域的成熟应用主要是为调谐质量阻尼器(TMD)提供阻尼单元,且多采用直线平板型[4-7].但板式ECD耗能效率偏低,难以直接应用于大型工程结构消能减振.在ECD的耗能减振效率提升方面,现阶段研究主要聚焦在板式ECD的构型或磁路优化层面[8-10].
近几年,机械工程领域“Inerter”[11](惯容器-两节点惯质单元)的引入为阻尼器研发提供了新的基本单元,阻尼器基本构型得到了丰富与发展[12].惯质单元可产生远大于自身实际物理质量的惯性(虚)质量,具体结构实现形式主要可分为滚珠丝杠、齿轮齿条、杠杆机构与液力式等[13-16].土木工程结构耗能减振领域阻尼器研发主要采用滚珠丝杠两节点惯质单元,如黏滞惯性质量阻尼器(VMD)[17]、串联黏滞质量阻尼器(SVMD)[18]、电磁惯性质量阻尼器(EIMD)[19]、轴向电涡流阻尼器[20]、调谐黏滞质量阻尼器[21]与电磁调谐双质阻尼器[22]等.研究结果表明[17-20]:具有被动负刚度特性的惯质阻尼器具有较好的耗能减振效果.
为提升ECD的耗能减振效率,推广ECD的工程应用范围,本文融合滚珠丝杠两节点惯质单元和ECD技术发展与研制了一种具有阻尼非线性特征的新型轴向旋转式电涡流惯质阻尼器,即非线性电涡流惯质阻尼器(NEMD).NEMD的滚珠丝杠机构使惯性飞轮与阻尼器旋转部件产生远大于自身实际物理质量的惯性质量的同时,对旋转式ECD导体切割磁力线的速度产生加速效应,可实现阻尼器惯性质量与电涡流阻尼的双重增效,同时通过特殊构造设计实现了ECD的非线性阻尼特征.综合NEMD电涡流阻尼的半理论半仿真、三维电磁场有限元仿真与样机力学性能测试,阐明了NEMD的轴向出力特性与设计流程,可为NEMD的工程应用提供参考.
1 NEMD样机构造与工作原理 1.1 样机构造图 1给出了NEMD的构造示意,其主要由滚珠丝杠传动系统与旋转部件构成的惯质单元以及滚珠丝杠传动系统与旋转式电涡流阻尼元件构成的阻尼单元并联而成.滚珠丝杠传动系统包括滚珠丝杆和套装在丝杆上的滚珠螺母,惯性飞轮套装于滚珠丝杆并和滚珠螺母固定为一体,随滚珠螺母同步旋转运动的所有物理质量产生惯性质量效应.旋转式电涡流阻尼元件包括固定于滚珠螺母两端的上下导磁钢板、固定在导磁钢板表面的矩形永磁体组和置于导磁钢板之间的导体铜板.其中永磁体沿上、下导磁钢板表面均匀对称布置,上、下对称两块永磁体定义为一组,每组永磁体相互吸引.采用直线导轨和连接杆将导体铜板和滚珠丝杆连接成整体,通过上、下推力轴承将滚珠丝杠传动系统、旋转式电涡流阻尼元件和惯性飞轮内置于阻尼器外筒.

|
图 1 非线性电涡流惯质阻尼器(NEMD)整体构造示意 Fig. 1 Configuration sketch of a nonlinear eddy-current inertial mass damper (NEMD) |
据此研制的NEMD样机内部构造见图 2,相关设计参数见表 1.其中:导磁钢板选用低碳钢;导体铜板选用高电导率的紫铜板;矩形永磁体采用N50型NdFeB,沿上、下导磁钢板表面均匀对称布置24组;导磁钢板内、外圈永磁体中心到丝杆中心距离分别为43 mm与68 mm;导体铜板与上、下永磁体之间的初始净矩hg均为15 mm.

|
图 2 NEMD样机 Fig. 2 Prototype of the NEMD |
| 表 1 NEMD样机参数 Tab. 1 Parameters of the NEMD prototype |
当图 1所示NEMD上、下连接端分别与结构内部存在相对位移的两节点相连,阻尼器两端连接点之间的相对轴向运动则转化为导磁钢板和惯性飞轮的高速旋转运动,同时滚珠丝杆和导体铜板随结构振动做同步直线运动,导磁钢板和惯性飞轮的高速旋转运动产生的转动惯性矩及导体铜板切割永磁体组磁力线产生的电涡流阻尼力矩经滚珠丝杠传动系统进一步放大分别形成轴向惯性力和电涡流阻尼力.忽略NEMD内部相对较小的机械摩擦力影响,NEMD总轴向力可表示为
| $ {F_{\rm{d}}} = {F_{\rm{a}}} + {F_{\rm{e}}}, $ | (1) |
式中Fa与Fe分别表示NEMD的惯性力与电涡流阻尼力.
惯性力Fa和惯性质量ma[20]计算式:
| $ {F_{\rm{a}}} = {m_{\rm{a}}}\ddot u, $ | (2) |
| $ {m_{\rm{a}}} = \frac{{4{\pi ^2}}}{{{\eta ^2}L_{\rm{d}}^2}}{J_{\rm{w}}}, $ | (3) |
式中:Ld与η分别表示滚珠丝杠的导程与滚珠丝杠传动系统的逆传动效率,Jw表示NEMD旋转部件的总转动惯量,ü表示NEMD的轴向加速度.
将永磁体组与铜板之间的相对瞬时旋转运动近似处理为二者的相对直线运动后,忽略相邻永磁体之间的耦合作用,可将NEMD阻尼单元分解为单体(单组永磁体与铜板之间的相对直线运动)后再进行叠加分析.由图 3所示的NEMD阻尼单元单体计算模型可知,永磁体中心线速度vr为

|
图 3 NEMD阻尼单元单体计算模型示意 Fig. 3 Damping calculation model of the NEMD monomer |
| $ {v_{\rm{r}}} = \frac{{{d_i}}}{2}\dot \varphi = \frac{{{d_i}}}{2} \times \frac{{2\pi }}{{\eta {L_{\rm{d}}}}}\dot u = \frac{{\pi {d_i}}}{{\eta {L_{\rm{d}}}}}\dot u, $ | (4) |
式中:di表示永磁体到滚珠丝杆的中心距,
关于滚珠丝杆中轴线中心对称的两组永磁体分别与导体铜板作用产生电涡流效应形成的洛伦兹力形成一对力偶,电涡流总阻尼力矩则由多对力偶叠加而成.每组永磁体中间同一水平投影面视为匀强磁场Bz,若忽略电涡流的趋肤效应和反抗磁场影响,则每组永磁体产生的洛伦兹力F[4]和相应对称两组永磁体对应的电涡流总阻尼力矩Te为:
| $ F = - {v_{\rm{r}}}\sigma \delta sB_{\rm{z}}^2{\mathop{\rm sign}\nolimits} \left( {{v_{\rm{r}}}} \right), $ | (5) |
| $ {T_{\rm{e}}} = 2\sum\limits_{i = 1}^n F {d_i}. $ | (6) |
式中:σ表示导体铜板的电导率,δ表示导体铜板厚度,s表示单块永磁体磁场的平面投影面积,Bz表示导体铜板位置处的主磁感应强度,n表示洛伦兹力力偶对数,sign()表示符号函数.
则NEMD电涡流阻尼力Fe可表示为
| $ {F_{\rm{e}}} = \frac{{2\pi }}{{\eta {L_{\rm{d}}}}}{T_{\rm{e}}}, $ | (7) |
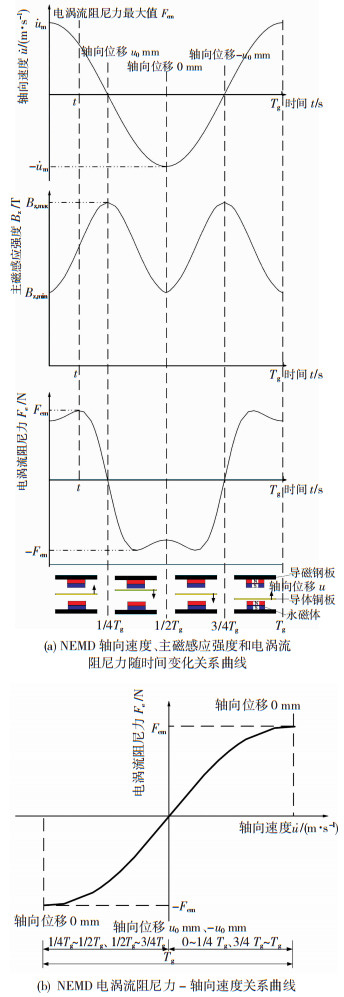
为阐明NEMD电涡流阻尼力的非线性特征,本节先以NEMD(单组永磁体)受到振动周期Tg、振幅u0的正弦激振为例,采用图解法(图 4)进行定性分析,后续拟通过有限元仿真分析与实验定量验证.
|
图 4 NEMD电涡流阻尼力非线性演化规律 Fig. 4 Nonlinear evolution of eddy-current damping force of the NEMD |
图 4(a)给出了一个完整周期Tg内NEMD的轴向速度
由上述分析可知NEMD易实现阻尼器阻尼系数与惯性质量的参数调节:通过变化导体铜板厚度、导磁钢板初始间距,或改变永磁体数量、尺寸和等级等,均可实现阻尼器的电涡流阻尼力调节;通过变化惯性飞轮的转动惯量可实现阻尼器的惯性力调节.
2 NEMD电涡流阻尼力分析 2.1 半理论半仿真分析由式(5)~(7)可知,速度vr一定时,NEMD电涡流阻尼力Fe完全由主磁感应强度Bz决定,而Bz可通过三维电磁场有限元仿真分析软件COMSOL Multiphysics计算得到.因此,Fe可通过半理论半仿真方法近似确定,本节以NEMD振动频率2.0 Hz、振幅10 mm为例说明轴向速度最大时电涡流阻尼力的计算过程.首先通过三维电磁场有限元仿真得到NEMD轴向速度最大时导体铜板位置处Bz为0.101 0 T,由式(4)计算得到内、外圈单组永磁体对应的洛伦兹力F分别为2.676 9、4.233 2 N,其中vr分别取NEMD轴向速度最大时对应的内、外圈单组永磁体中心的线速度3.772 4、5.965 6 m/s;接着通过式(6)得到Te为4.835 6 N·m;最后通过式(7)得到Fe幅值为3 376 N.
2.2 有限元仿真分析同样采用“单体叠加”方法,对NEMD样机的电涡流阻尼进行电磁场有限元仿真分析.试算发现:当导体板尺寸能够覆盖永磁体产生的磁感应强度时,继续增大导体板平面尺寸对电涡流阻尼力增量影响很小,本节导体铜板平面尺寸统一取100 mm×100 mm.采用COMSOL准静态分析模块AC/DC瞬态分析方法对单组永磁体电涡流阻尼进行有限元仿真,获得洛伦兹力F,然后通过式(6)计算得到Te,最后采用式(7)换算得到Fe.
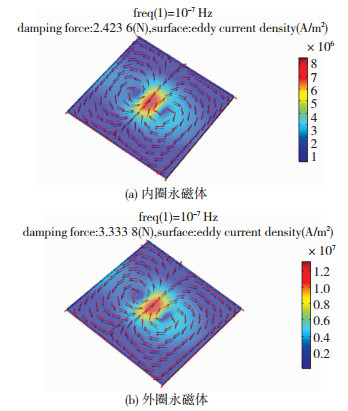
图 5(a)、(b)给出了NEMD振动频率2.0 Hz、轴向速度最大时,内外圈单组永磁体分别对应的导体铜板表面的电涡流密度分布与洛伦兹力大小(分别为2.423 6、3.333 8 N),据此通过式(6)和式(7)换算得到Fe幅值为2 772 N.
|
图 5 导体铜板表面电涡流密度分布 Fig. 5 Eddy current densities distribution on the surface of the copper plate |
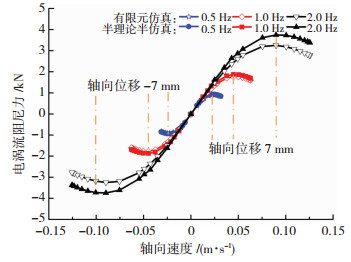
图 6和图 7分别对比了半理论半仿真和有限元仿真获得的NEMD电涡流阻尼力-轴向位移滞回关系曲线、电涡流阻尼力-轴向速度关系曲线.由图可知:各工况电涡流阻尼力均随速度增大表现出先上升后下降的非线性特征,且最大阻尼力对应的轴向位移绝对值均为7 mm;NEMD振动频率较低(0.5 Hz、1.0 Hz)时,NEMD电涡流阻尼力半理论半仿真和有限元仿真结果整体吻合较好;当NEMD振动频率较高(2.0 Hz)时,电涡流阻尼力半理论半仿真结果大于有限元仿真结果.主要原因:不同于有限元仿真,半理论半仿真无法考虑客观必然存在的电涡流集肤效应和反抗磁场作用,且振动频率越高,导体铜板形成的电涡流强度越强,则电涡流集肤效应和反抗磁场作用越大,对电涡流阻尼力幅值的削弱作用也越强.

|
图 6 NEMD电涡流阻尼力-轴向位移滞回关系仿真曲线 Fig. 6 Numerical hysteresis curves between the eddy-current damping force and axial displacement of the NEMD |
|
图 7 NEMD电涡流阻尼力-轴向速度关系仿真曲线 Fig. 7 Numerical eddy-current damping force of the NEMD versus its axial velocity |
NEMD样机力学性能测试系统见图 8,通过偏心轮激振机构对NEMD样机进行简谐位移激振,振幅保持10 mm不变(激振频率分别设定为0.5 Hz、1.0 Hz与2.0 Hz);采用动态信号采集系统记录NEMD的轴向力和轴向位移信号.

|
图 8 NEMD样机力学性能测试系统 Fig. 8 Mechanical property testing system of the NEMD prototype |
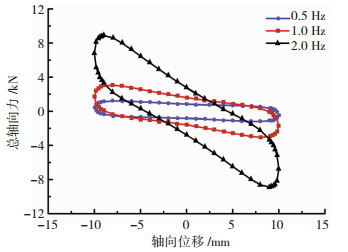
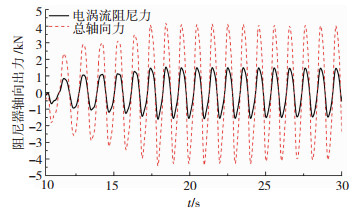
图 9给出了NEMD样机轴向力-轴向位移滞回关系曲线测试结果,阻尼器表现出预期的惯性质量负刚度效应,且激振频率越高,负刚度效应越显著.图 10给出了NEMD样机的总轴向力与电涡流阻尼力典型时程曲线,其中电涡流阻尼力
|
图 9 NEMD总轴向力-轴向位移滞回关系曲线 Fig. 9 Hysteresis curves between the total axial force and axial displacement of the NEMD |
|
图 10 NEMD轴向出力时程曲线(振动频率1.0 Hz) Fig. 10 Axial force time histories of the NEMD (Vibration frequency: 1.0 Hz) |
| $ {F_{\rm{e}}}(t) = {F_{\rm{d}}}(t) - {m_{\rm{a}}}\ddot u(t), $ | (8) |
式中:Fe(t)与Fd(t)分别表示NEMD的电涡流阻尼力与总轴向力,ü(t)表示NEMD轴向加速度,惯性质量ma可通过式(3)计算,具体数值为6247.18 kg.
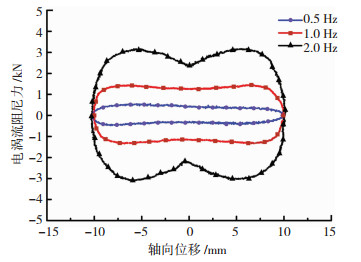
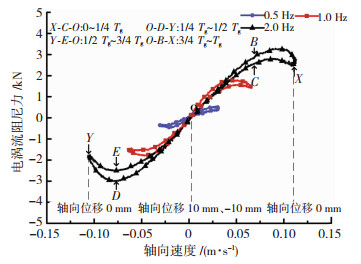
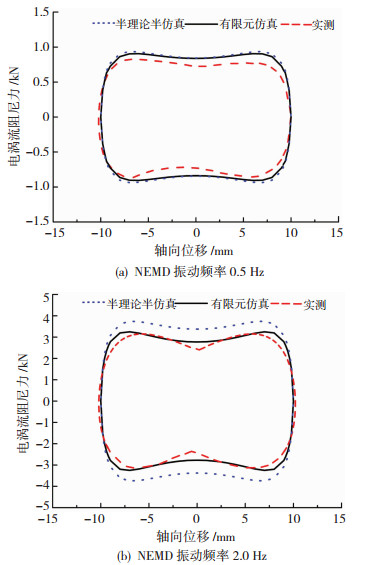
图 11、12分别给出了NEMD电涡流阻尼力与轴向位移、电涡流阻尼力与轴向速度关系实测曲线.对比图 11和图 6结果(见图 13)可知,半理论半仿真与有限元仿真得到的NEMD电涡流阻尼力-轴向位移关系曲线均和实测结果整体趋势一致,但随着NEMD轴向位移逐渐接近0,半理论半仿真、有限元仿真与实测结果的相对误差均逐渐增大,这主要是由于NEMD轴向位移为0(速度最大)时,半理论半仿真和有限元仿真均会过高估计NEMD导体铜板位置的主磁感应强度.此外,对比图 12和图 7可知,半理论半仿真与有限元仿真得到的NEMD电涡流阻尼力-轴向速度关系曲线和实测结果均表现出先上升后下降的非线性特征,主要差别在于速度较大时实测结果出现环路现象,且NEMD振动频率越大环路特征越显著.
|
图 11 NEMD电涡流阻尼力-轴向位移滞回关系实测曲线 Fig. 11 Experimental hysteresis curves between the eddy-current damping force and axial displacement of the NEMD |
|
图 12 NEMD电涡流阻尼力-轴向速度关系实测曲线 Fig. 12 Experimental eddy-current damping force of the NEMD versus its axial velocity |
|
图 13 NEMD电涡流阻尼力-轴向位移滞回关系曲线 Fig. 13 Hysteresis curves between the eddy-current damping force and axial displacement of the NEMD |
NEMD电涡流阻尼力-轴向速度关系曲线出现环路的原因:1)导体铜板切割磁感线产生电涡流,电涡流产生反抗磁场,而反抗磁场与NEMD轴向速度之间存在相位差,具体表现为反抗磁场滞后于NEMD轴向速度;2) NEMD轴向速度越大,电涡流强度越大,则激发的反抗磁场也越大,而NEMD电涡流阻尼力幅值必然受到前一时刻电涡流反抗磁场的不利影响,导致速度大小相同“速度由小变大”(图 12 B点)时的电涡流阻尼力大于“速度由大变小”(图 12 C点)时的电涡流阻尼力;3) NEMD振动频率越高(振幅不变),电涡流强度越高,反抗磁场影响程度就越大,导致曲线环路特征也越显著.
表 2对比了NEMD样机电涡流阻尼力幅值的半理论半仿真、有限元仿真和试验结果:
| 表 2 电涡流阻尼力幅值半理论半仿真分析、有限元仿真和试验结果对比 Tab. 2 Comparisons among approximate theoretical analysis, finite element simulation, and test results of the eddy-current damping force |
1) 与试验结果相比,半理论半仿真与有限元仿真均会高估电涡流阻尼力幅值.主要原因:半理论半仿真完全忽略了电涡流集肤效应和反抗磁场的影响以及相邻永磁体之间的耦合作用,有限元仿真虽然可考虑电涡流集肤效应和反抗磁场的作用,但同样无法考虑相邻永磁体之间的耦合效应.
2) 半理论半仿真与试验结果之间的相对误差均在20%以内,而有限元仿真与试验结果之间的相对误差均在10%以内,表明本文提出的半理论半仿真与有限元仿真方法有望用于NEMD电涡流阻尼力的预测分析.
4 NEMD设计方法NEMD惯质单元通过理论公式即可实现精准设计[19-20],而电涡流阻尼单元若采用半理论半仿真方法计算误差相对较大,仅适用于初步设计,需通过三维电磁场有限元仿真分析进一步深化设计.因此,NEMD可采用如下所述的两阶段设计方法.
1) 第一阶段(初步设计)
a) 首先确定NEMD目标出力(含阻尼力和惯性力比例)、行程;
b) 初定滚珠丝杠和导磁钢板、导体铜板和永磁体组件等参数;
c) 采用COMSOL Multiphysics软件仿真得到单组永磁体中心位置的主磁感应强度,由式(5)计算得到单组永磁体与导体铜板相对运动产生电涡流效应形成的洛伦兹力;
d) 通过式(6)、(7)计算得到所需的总洛伦兹力,以及洛伦兹力力偶对数n,即永磁体沿上下导磁钢板表面垂直于滚珠丝杆中轴线方向均匀对称布置2n组;
e) 通过式(2)、(3)计算得到附加惯性飞轮转动惯量Jw,选取惯性飞轮尺寸大小.
2) 第二阶段(最终设计)
a) 采用COMSOL Multiphysics软件准静态分析模块AC/DC的瞬态分析方法对单组永磁体电涡流阻尼进行三维电磁场有限元仿真,获得单组永磁体对应的洛伦兹力;
b) 通过式(6)计算得到NEMD电涡流阻尼力矩,然后采用式(7)换算得到电涡流阻尼力;
c) 与NEMD电涡流阻尼力目标设计值进行对比,校核初步设计结果,不断调整初步设计方案直至满足设计目标要求.
5 结论1) 融合滚珠丝杠两节点惯质单元和旋转式电涡流阻尼技术提出的新型阻尼器NEMD使惯性飞轮产生远大于自身实际物理质量的惯性质量的同时,对阻尼器转速产生加速效应,实现了阻尼器惯性质量与电涡流阻尼的双重增效,且NEMD随着阻尼器轴向速度的增加,阻尼力表现出先上升后下降的非线性特征,显著提高了阻尼器耗能效率.
2) 电涡流集肤效应和反抗磁场作用对电涡流阻尼力幅值和出力特性均有较大影响,与半理论半仿真方法相比,三维电磁场有限元仿真可真实模拟这两者对电涡流阻尼力幅值的折减效应,显著提升NEMD旋转式电涡流阻尼单元的力学性能仿真精度.
3) 综合半理论半仿真和三维电磁场有限元仿真提出的NEMD两阶段设计方法,可为NEMD实用装置研发与工程应用提供有益参考.
| [1] |
寇宝泉, 金银锡, 张赫, 等. 电磁阻尼器的发展现状及应用前景[J]. 中国电机工程学报, 2015, 35(12): 3132. KOU Baoquan, JIN Yinxi, ZHANG He, et al. Development and application prospects of the electromagnetic damper[J]. Proceedings of the CSEE, 2015, 35(12): 3132. |
| [2] |
杨毅青, 徐东东. 基于电涡流阻尼器的数控加工振动抑制[J]. 振动与冲击, 2016, 35(4): 177. YANG Yiqing, XU Dongdong. Vibration suppression of NC machining based on eddy current dampers[J]. Journal of Vibration and Shock, 2016, 35(4): 177. |
| [3] |
王昊, 游进, 张志成. 电涡流阻尼器构型比较与阻尼特性研究[J]. 载人航天, 2017, 23(2): 197. WANG Hao, YOU Jin, ZHANG Zhicheng. Damper characteristic analysis and different configurations comparisons of eddy current damper[J]. Manned Spaceflight, 2017, 23(2): 197. DOI:10.3969/j.issn.1674-5825.2017.02.010 |
| [4] |
汪志昊, 陈政清. 永磁式电涡流调谐质量阻尼器的研制与性能试验[J]. 振动工程学报, 2013, 26(3): 374. WANG Zhihao, CHEN Zhengqing. Development and performance tests of an eddy-current tuned mass damper with permanent magnets[J]. Journal of Vibration Engineering, 2013, 26(3): 374. DOI:10.3969/j.issn.1004-4523.2013.03.010 |
| [5] |
华旭刚, 温青, 陈政清, 等. 大跨度双层曲线斜拉桥人致振动减振优化与实测验证[J]. 振动工程学报, 2016, 29(5): 822. HUA Xugang, WEN Qing, CHEN Zhengqing, et al. Design and experimental validation of structural vibration control of a curved twin-deck cable-stayed bridge subject to pedestrians[J]. Journal of Vibration Engineering, 2016, 29(5): 822. |
| [6] |
WANG W X, DALTON D, HUA X G, et al. Experimental study on vibration control of a submerged pipeline model by eddy current tuned mass damper[J]. Applied Sciences, 2017, 7(10): 987. DOI:10.3390/app7100987 |
| [7] |
LU X L, ZHANG Q, WENG D G, et al. Improving performance of a super tall building using a new eddy-current tuned mass damper[J]. Structural Control and Health Monitoring, 2017, 24(3): e1882. DOI:10.1002/stc.1882 |
| [8] |
陈政清, 张弘毅, 黄智文. 板式电涡流阻尼器有限元仿真与参数优化[J]. 振动与冲击, 2016, 35(18): 123. CHEN Zhengqing, ZHANG Hongyi, HUANG Zhiwen. FEM simulation and parameter optimization of a planar eddy current damper[J]. Journal of Vibration and Shock, 2016, 35(18): 123. |
| [9] |
汪志昊, 张闯, 周佳贞, 等. 新型装配式竖向电涡流TMD试验研究[J]. 振动与冲击, 2017, 36(1): 16. WANG Zhihao, ZHANG Chuang, ZHOU Jiazhen, et al. Experimental study on a prefabricated eddy-current TMD for vibration control of footbridges[J]. Journal of Vibration and Shock, 2017, 36(1): 16. |
| [10] |
ZHANG H, KOU B, JIN Y, et al. Modeling and analysis of a novel planar eddy current damper[J]. Journal of Applied Physics, 2014, 115(17): 19. DOI:10.1063/1.4862516 |
| [11] |
SMITH M C. Synthesis of mechanical networks:the inerter[J]. IEEE Transactions on Automatic Control, 2002, 47(10): 1648. DOI:10.1109/TAC.2002.803532 |
| [12] |
陈政清.三元被动减振理论与它的一种实现方式-电涡流轴向阻尼器[M]//中国工程院.防震减灾新技术.北京: 高等教育出版社, 2016: 40
|
| [13] |
毛明, 王乐, 陈轶杰, 等. 惯容器及惯容器-弹簧-阻尼器悬架研究进展[J]. 兵工学报, 2016, 37(3): 525. MAO Ming, WANG Le, Chen Yijie, et al. Research progress in inerter and inerter-spring-damper suspension[J]. Acta Armamentarii, 2016, 37(3): 525. DOI:10.3969/j.issn.1000-1093.2016.03.019 |
| [14] |
孙晓强, 陈龙, 汪少华, 等. 滚珠丝杠式惯容器非线性建模与参数辨识[J]. 振动、测试与诊断, 2016, 36(2): 329. SUN Xiaoqiang, CHEN Long, WANG Shaohua, et al. Nonlinear modeling and parameters identification of ball-screw inerter[J]. Journal of Vibration Measurement and Diagnosis, 2016, 36(2): 329. |
| [15] |
陈龙, 张孝良, 聂佳梅, 等. 基于半车模型的两级串联型ISD悬架性能分析[J]. 机械工程学报, 2012, 48(6): 102. CHEN Long, ZHANG Xiaoliang, NIE Jiamei, et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model[J]. Journal of Mechanical Engineering, 2012, 48(6): 102. |
| [16] |
陈龙, 任皓, 汪若尘, 等. 液力式惯容器力学性能仿真与试验研究[J]. 振动与冲击, 2014, 33(12): 87. CHEN Long, REN Hao, WANG Ruochen, et al. Simulations and tests for mechanical properties of a hydraulic inerter[J]. Journal of Vibration and Shock, 2014, 33(12): 87. |
| [17] |
IKAGO K, SAITO K, INOUE N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(3): 453. DOI:10.1002/eqe.1138 |
| [18] |
罗浩, 张瑞甫, 翁大根, 等. 一种旋转黏滞质量阻尼器对结构响应的控制研究[J]. 防灾减灾工程学报, 2016, 36(2): 295. LUO Hao, ZHANG Ruifu, WENG Dagen, et al. Study of a series viscous mass damper in the control of structural response[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(2): 295. |
| [19] |
NAKAMURA Y, FUKUKITA A, TAMURA K, et al. Seismic response control using electromagnetic inertial mass dampers[J]. Earthquake Engineering and Structural Dynamics, 2014, 43(4): 507. DOI:10.1002/eqe.2355 |
| [20] |
黄智文.电涡流阻尼器理论研究及其在桥梁竖向涡振控制中的应用[D].长沙: 湖南大学, 2016 HUANG Zhiwen. Theoretical study of eddy current damper and its application in vertical vortex induced vibration control of bridges[D]. Changsha: Hunan University, 2016 |
| [21] |
阎武通, 韩冰, 文永奎. 新型调谐黏滞质量阻尼器对斜拉桥的减震控制分析[J]. 土木工程学报, 2016, 49(增刊1): 66. YAN Wutong, HAN Bing, WEN Yongkui. Seismic control analysis of cable-stayed bridge based on tuned viscous mass damper[J]. China Civil Engineering Journal, 2016, 49(S1): 66. |
| [22] |
孙洪鑫, 罗一帆, 王修勇, 等. 电磁调谐双质阻尼器的参数优化及对结构减震分析[J]. 沈阳建筑大学学报(自然科学版), 2018, 34(3): 410. SUN Hongxin, LUO Yifan, WANG Xiuyong, et al. Parametric optimization and vibration control of electromagnetic tuned mass-inerter dampers for the structures[J]. Journal of Shenyang Jianzhu University (Natural Science), 2018, 34(3): 410. |
 2019, Vol. 51
2019, Vol. 51


