2. 东南大学 土木工程学院,南京 210096;
3. 北京建筑大学 北京未来城市设计高精尖创新中心,北京 100044
2. School of Civil Engineering, Southeast University, Nanjing 210096, China;
3. Beijing Advanced Innovation Center for Future Urban Design, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
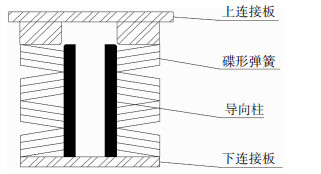
组合碟形弹簧(简称“碟簧”)具有构造简单、刚度可控、有摩擦耗能能力等优点,因此组合碟簧常用于建筑结构的竖向隔震装置[1-2].组合碟簧竖向隔震装置(DSI装置)的典型构造见图 1,该装置由上连接板、组合碟簧、导向柱和下连接板组成.
|
图 1 DSI装置 Fig. 1 DSI device |
DSI装置的刚度特性及阻尼特性是影响其隔震性能的重要参数.文献[3-4]对DSI装置的阻尼特性进行试验研究,研究表明叠合碟簧可增加DSI装置的阻尼耗能能力,加载速率对DSI装置的阻尼特性影响不大.文献[5-6]对DSI装置进行静态及动态试验,研究表明DSI装置的阻尼耗能能力与碟簧的组合片数、叠合方式和预压位移有关.文献[7-8]利用数值模拟方法研究了DSI装置的力学性能,研究表明,静力单调加载工况下,设置B系列碟簧DSI装置的荷载-位移曲线未呈明显的二次曲线变化趋势,可将其刚度假定为定值进行考虑.文献[9]对DSI装置的受力性能进行静力和动力往复加载性能试验研究,研究表明,DSI装置的荷载-位移滞回曲线具有典型的不对称性特征,DSI装置的加载刚度明显大于其卸载刚度.
目前,关于DSI装置力学性能的研究已有一定基础,但DSI装置的恢复力模型通常采用线性模型[10-11]、双线性模型[12-13]等对称性恢复力模型,这与DSI装置实际受力状态中的非对称性荷载-位移滞回关系存在显著区别,因此有必要建立DSI装置的非对称恢复力模型,以便更准确地分析其力学特性,从而对其等效刚度及等效阻尼比进行有效评价.为了研究DSI装置的非对称恢复力模型,本文首先对DSI装置的受力机理进行分析,在此基础上建立DSI装置的非对称恢复力模型-原点指向恢复力模型(OO恢复力模型).最后,对典型DSI装置进行力学性能试验,并利用试验结果对OO恢复力模型的有效性进行验证.
1 DSI装置的受力机理分析 1.1 单片碟簧的力学性能单片碟簧承受的荷载Fs与位移f关系可表述为[14]
| $ {F_{\rm{s}}} = \frac{{4E}}{{1 - {\mu ^2}}}\frac{{{t^4}}}{{{M_1}{D^2}}}\frac{f}{t}\left[ {\left( {\frac{{{h_0}}}{t} - \frac{f}{t}} \right)\left( {\frac{{{h_0}}}{t} - 0.5\frac{f}{t}} \right) + 1} \right], $ | (1) |
| $ {F_{\rm{c}}} = \frac{{4E}}{{1 - {\mu ^2}}}\frac{{{h_0}{t^3}}}{{{M_1}{D^2}}}. $ | (2) |
式中:E、μ分别为碟簧材料的弹性模量及泊松比;t、h0分别为碟簧的厚度及压缩行程;当碟簧的变形为f=h0时,碟簧的承载力Fc可用式(2)表示;M1与碟簧外径D、内径d之比c= D/d相关,其表达式为
| $ {M_1} = \frac{1}{\pi }{\left( {\frac{{c - 1}}{c}} \right)^2}/\left( {\frac{{c + 1}}{{c - 1}} - \frac{2}{{\ln c}}} \right), $ | (3) |
由式(1)~(3)可确定单片碟簧荷载与位移的关系.
1.2 DSI装置的受力机理DSI装置的摩擦耗能来源为4个部分(图 2):1)结构内部材料的变形及摩擦;2)碟簧与上、下连接板之间的摩擦;3)碟簧与导向柱之间的摩擦;4)相邻碟簧片之间的摩擦.由于在DSI装置中,碟簧与导向柱之间的摩擦一般较小,因此,在本文计算分析过程中,忽略了碟簧与导向柱之间的摩擦.

|
图 2 DSI装置的摩擦力示意 Fig. 2 Friction forces in DSI device |
DSI装置阻尼力由两部分构成:1)黏性阻尼力,大小与加载速率成正比,方向与加载方向相反,该部分黏性阻尼力考虑了结构内部材料的变形及摩擦,因此在库仑阻尼力中不重复考虑;2)库仑阻尼力,主要由碟簧锥面间摩擦及碟簧与上、下连接板之间的摩擦形成,方向与加载方向相反.
1.3 DSI装置的受力性能加载时摩擦力使DSI装置负荷增大,卸载时摩擦力使DSI装置负荷减小.加载工况下,考虑摩擦力影响时的DSI装置的荷载FRj与单片碟簧的荷载Fs之间的关系表达式为[12]
| $ {F_{{\rm{Rj}}}} = {F_{\rm{s}}}\frac{n}{{1 - {f_{\rm{M}}}(n - 1) - {f_{\rm{R}}}}}, $ | (4) |
卸载工况下,考虑摩擦力影响时的DSI装置的荷载FRx与单片碟簧的荷载Fs之间的关系表达式为[12]
| $ {F_{{\rm{Rx}}}} = {F_{\rm{s}}}\frac{n}{{1 + {f_{\rm{M}}}(n - 1) + {f_{\rm{R}}}}}, $ | (5) |
式中:fM为碟簧锥面间的摩擦系数, fR为碟簧承载边缘处的摩擦系数,n为DSI装置中碟簧组的叠合数.
2 DSI装置的恢复力模型 2.1 基本假定1) DSI装置在预压荷载(结构重力)作用下,达到静平衡状态后的加载刚度和卸载刚度近似呈线性变化,因此OO恢复力模型仅适用于A系列和B系列碟簧组成的DSI装置[15].
2) 忽略DSI装置中碟簧与中心导向柱之间的摩擦.
3) DSI装置中碟簧的横截面不发生扭曲,且沿着某中心点进行旋转.
4) DSI装置中碟簧的径向应力及应变均很小,可忽略.
2.2 原点指向恢复力模型基于DSI装置的受力特性,提出图 3所示原点指向恢复力模型.由于该恢复力模型中加载刚度和卸载刚度均指向原点,因此称其为原点指向恢复力模型(OO恢复力模型).k1为加载刚度,k2是下降段刚度,k3是卸载刚度.随着荷载作用的过程,曲线沿O、A、B、C、D…顺序前进.此模型需要3个参数k1、k2和k3才能确定.

|
图 3 原点指向恢复力模型 Fig. 3 OO hysteretic model |
加载刚度k1:令式(4)中DSI装置的荷载FRj等于预压荷载FGj,即FRj=FGj,则FGj作用下(加载工况)单片碟簧的荷载Fsj可表示为
| $ {F_{{\rm{sj}}}} = {F_{{\rm{Gj}}}}\frac{{1 - {f_{\rm{M}}}(n - 1) - {f_{\rm{R}}}}}{n}. $ | (6) |
然后利用式(1)中单片碟簧的荷载Fsj与其位移的关系计算出对应的位移fGj.利用式(7)即可算得DSI装置的加载刚度k1:
| $ {k_1} = {F_{{\rm{Gj}}}}/\left( {m{f_{{\rm{Gj}}}}} \right), $ | (7) |
式中m为DSI装置中碟簧组的对合数.
卸载刚度k3:令式(5)中DSI装置的荷载FRx等于预压荷载FGx,即FRx=FGx,则FGx作用下(卸载工况)单片碟簧的荷载Fsx可表示为
| $ {F_{{\rm{sx}}}} = {F_{{\rm{Gx}}}}\frac{{1 + {f_{\rm{M}}}(n - 1) + {f_{\rm{R}}}}}{n}. $ | (8) |
然后利用式(1)中单片碟簧的荷载Fsj与其位移的关系计算出对应的位移fGx.利用式(9)即可算得DSI装置的卸载刚度k3:
| $ {k_3} = {F_{{\rm{Gx}}}}/\left( {m{f_{{\rm{Gx}}}}} \right). $ | (9) |
加载工况下DSI装置中的摩擦力大小为
| $ {F_{{\rm{fj}}}} = {F_{{\rm{Rj}}}}\left( {{f_{\rm{M}}}(n - 1) + {f_{\rm{R}}}} \right), $ | (10) |
卸载工况下DSI装置中的摩擦力大小为
| $ {F_{{\rm{fx}}}} = {F_{{\rm{Rx}}}}\left( {{f_{\rm{M}}}(n - 1) + {f_{\rm{R}}}} \right). $ | (11) |
在下降段中,从B点到C点过程中,DSI装置中的摩擦力完全反向,下降段BC间的位移lxj近似取为
| $ {l_{{\rm{xj}}}} = \left( {{f_{{\rm{Gj}}}} - {f_{{\rm{Gx}}}}} \right)m. $ | (12) |
结合图 3中DSI的恢复力与位移的关系,下降段刚度k2可表示为
| $ {k_2} = \left( {{k_1}{f_{{\rm{Gj}}}} - {k_3}{f_{{\rm{Gx}}}}} \right)m/{l_{{\rm{xj}}}}. $ | (13) |
OO恢复力模型要解决的问题是要判别DSI装置所处的变形状态,继而写出其恢复力的表达式.
2.3.1 状态判别条件OO恢复力模型由三类直线组成(图 4):上缓线(如OA段、AB段);陡线(如DA段、BC段);下缓线(如CD段、DO段).设用PD表示状态判定数,并规定:上缓线,PD=+1;陡线,=PD=0;下缓线,PD== -1.状态判定数在图 3中圆括号内进行表示.

|
图 4 OO恢复力模型的计算流程图 Fig. 4 Flow chart of OO hysteretic model |
记某一段陡线顶点的水平坐标为xt,陡线底点的水平坐标为xb.下面按加载顺序写出状态条件及相应的恢复力表达式:
| $ \begin{array}{l} O \to A, {\rm{PD}} = + 1, \dot x > 0, P = {k_1}x;\\ A \to B, {\rm{PD}} = + 1, \dot x > 0, P = {k_1}x;\\ B \to C, {\rm{PD}} = 0, \dot x < 0, P = {k_1}{x_{{\rm{t - B}}}} - {k_2}\left( {x - {x_{{\rm{b}} - {\rm{C}}}}} \right);\\ C \to D, {\rm{PD}} = - 1, \dot x < 0, P = {k_3}x;\\ D \to A, {\rm{PD}} = 0, \dot x > 0, P = {k_3}x + {k_2}\left( {x - {x_{{\rm{b}} - {\rm{D}}}}} \right);\\ A \to {B^\prime }, {\rm{PD}} = + 1, \dot x > 0, P = {k_1}x;\\ \ldots \end{array} $ | (14) |
式中:x为DSI装置的位移,xt-B、xb-C分别为陡线BC的顶点及底点坐标,xb-D为陡线AD的底点坐标.
2.3.3 符号规定1) 正向加载时,速度ẋ>0,反向加载时,速度ẋ<0;
2) 当x在陡线DA上时,x应满足下式
| $ \left| {{x_{{\rm{t}} - {\rm{A}}}} - x} \right| < \left| {{x_{{\rm{t}} - {\rm{A}}}} - {x_{{\rm{b}} - {\rm{D}}}}} \right|, $ | (15) |
当x在陡线BC上时,x应满足下式
| $ \left| {{x_{{\rm{t}} - {\rm{B}}}} - x} \right| < \left| {{x_{{\rm{t}} - {\rm{B}}}} - {x_{{\rm{b}} - {\rm{C}}}}} \right|. $ | (16) |
3) 当x从陡线DA过渡到缓线AB时,速度ẋ不变号;但x应满足下式
| $ \left| {{x_{{\rm{t}} - {\rm{A}}}} - x} \right| \ge \left| {{x_{{\rm{t}} - {\rm{A}}}} - {x_{{\rm{b}} - {\rm{D}}}}} \right|, $ | (17) |
当x从陡线BC过渡到缓线CD时,速度ẋ不变号;但x应满足下式
| $ \left| {{x_{{\rm{t}} - {\rm{B}}}} - x} \right| \ge \left| {{x_{{\rm{t}} - {\rm{B}}}} - {x_{{\rm{b}} - {\rm{C}}}}} \right|. $ | (18) |
4) 从缓线向陡线过渡时,速度ẋ变号.
综合以上规律,可把用于恢复力计算的状态判别条件和符号规定写成图 4所示流程图.
2.3.4 基于OO恢复力模型的DSI装置动力分析DSI装置的动力微分方程为:
| $ m\ddot x + c\dot x + P = {F_{\rm{w}}}, $ | (19) |
式中:m为DSI装置所承受预压荷载相对应的质量,即DSI装置所承受上部建筑物的质量;P为DSI装置的恢复力;Fw为外荷载;c为DSI装置的等效黏滞阻尼系数,其表达式为
| $ c = 2\zeta \sqrt {m{k_1}} , $ | (20) |
式中ζ为DSI装置中碟簧材料的阻尼比.
DSI装置的动力分析具体分为以下步骤:
1) 用数值积分方法求解DSI装置的动力微分方程(19),可求出第i步的位移x(i)和速度ẋ(i);并计算出该步计算过程中,陡线的顶点水平坐标xt(i)及底点水平坐标xb(i).
2) 基于步骤1)的计算结果,可按图 4所示关系判断下一步积分的状态判定数PD.
3) 用式(14)求出第i+1步数值分析时DSI装置的恢复力P(i+1).
4) 将第3)步的恢复力P(i+1)的计算结果和外荷载Fw(i+1)带入式(19),即可用数值积分方法计算出第i+1步时DSI装置的位移x(i+1)和速度ẋ(i+1).
循环计算步骤1)~4),即可完成DSI装置的动力响应计算.
3 试验方案 3.1 试验模型为了验证DSI装置的OO恢复力模型的有效性,对图 5所示的DSI装置试验模型(模型E)进行往复加载试验.模型E由12片碟簧组成,采取3片叠合,4组对合的组合方式.试验用碟簧参数见表 1.

|
图 5 DSI装置实物图 Fig. 5 Experimental model of DSI device |
| 表 1 碟簧参数 Tab. 1 Design parameters of disc spring |
采用MTS电液伺服系统进行模型试验加载,采用计算机采集试验模型的竖向荷载和位移值.对模型E进行不同加载预压位移作用下的往复加载试验,每个工况进行5个往复位移加载.记录不同的加载预压位移、加载频率和动荷载幅值工况下模型E的荷载-位移滞回曲线.加载预压位移dy分别取6、10和14 mm,加载频率f分别取0.1、0.2、0.5和1 Hz,动荷载幅值da分别取0.5、1、2和4 mm.加载工况及编号见表 2.
| 表 2 试验工况 Tab. 2 Test cases |
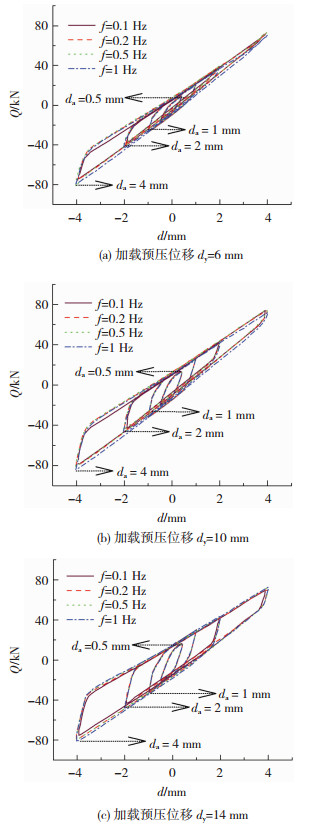
以加载预压位移作用下模型E的位置为坐标零点,定义其相对应的荷载值为零.各种工况下,模型E的典型荷载-位移(Q-d)滞回曲线见图 6.
|
图 6 模型E碟簧的荷载-位移曲线 Fig. 6 Load-displacement curves for Model E |
1) 由于加载刚度及卸载刚度的不同,模型E的荷载-位移滞回曲线呈明显不对称性形状.模型E的阻尼力主要来自于碟簧片间及碟簧与上、下连接板间的摩擦力,而摩擦力的大小与压力有关,加载时碟簧的压力逐渐增大,使得摩擦阻尼力逐渐增大,荷载-位移滞回曲线趋于饱满;卸载时,随着碟簧的竖向压缩变形量的减小,其变形能减小,同时碟簧间及碟簧与上、下连接板间产生的摩擦阻尼也减小,使得荷载-位移滞回曲线趋于细长,饱满度逐渐减小,从而导致模型E的荷载-位移滞回曲线具有明显的不对称性.
2) 随着动荷载幅值的增加,模型E荷载-位移滞回曲线的饱满度逐渐减小,不对称性逐渐增强.
3) 加载频率的变化对模型E的荷载-位移滞回曲线影响较小.由2.2节的分析可知,模型E的阻尼力包括库仑阻尼力和黏性阻尼力.黏性阻尼力的大小与加载速率成正相关关系,加载速率对库仑阻尼力的影响较小,由于模型E的荷载-位移滞回曲线受加载频率的影响较小,因此模型E的库仑阻尼力占主要部分,黏性阻尼力所占比重较小.
4) 随着加载预压位移的增加,模型E的荷载-位移滞回曲线趋于饱满,表明其耗能能力逐渐增强.随着加载预压位移的增大,DSI装置中碟簧的竖向变形和竖向荷载逐渐增大,其相应的库仑摩擦耗能和变形能也逐渐越大,从而导致DSI装置的荷载-位移滞回曲线随着加载预压位移的增加趋于饱满.
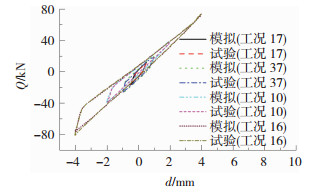
4.2 试验结果与简化模型模拟结果的对比分析以第3节中OO恢复力模型的理论分析为基础,利用MATLAB软件编写DSI装置的动力分析计算程序,数值积分采用Wilson-θ法.利用该程序对模型E的力学行为进行模拟.碟簧锥面间的摩擦系数fM取为0.016;碟簧承载边缘处的摩擦系数fR取为0.03;碟簧材料的阻尼比ζ取0.02.式(19)各参数的取值为:加载预压位移dy为6、10和14 mm时,所对应的上部建筑物质量m分别为11 177、19 374和26 834 kg;等效黏滞阻尼系数c分别为18 250、24 510和28 690 (N·s)/m;P为DSI装置的恢复力,由式(14)计算;Fw为外荷载,为力传感器所采集的荷载时程.图 7为动荷载作用下模型E荷载-位移滞回曲线试验结果和简化模型模拟结果的比较,限于篇幅仅列出工况10、16、17和工况37的计算结果.由图 8可知,在动荷载工况下,模型E荷载-位移滞回曲线的模拟值与试验值具有相似的曲线特征,简化模型模拟的结果与试验结果吻合较好.但在动荷载幅值较大的情况下,简化模型的分析结果与试验结果之间存在一定的差异,这些差异主要来自于基本假定对简化模型分析结果的影响:1)简化模型分析过程中假定模型E的加载刚度和卸载刚度近似呈线性变化,而模型E的实际加载刚度和卸载刚度均呈曲线变化;2)简化模型分析过程中忽略了碟簧组与导向柱之间的摩擦;3)不同加载频率工况下,模型的荷载-位移滞回曲线略有不同,但简化模型分析过程中并没有考虑加载频率对其分析结果的影响.
|
图 7 动荷载作用下模拟值和试验值比较 Fig. 7 Comparison of experimental results and simulation results under dynamic loadings |
模型E的等效刚度Kv为
| $ {K_{\rm{v}}} = \frac{{{Q_1} - {Q_2}}}{{{d_1} - {d_2}}}, $ | (21) |
式中:d1为加载方向最大位移,d2为卸载方向最大位移,Q1为与d1相对应的荷载值,Q2为与d2相对应的荷载值.
模型E的等效阻尼比ζV为
| $ {\zeta _{\rm{v}}} = \frac{{{\omega _{\rm{D}}}}}{{4\pi {\omega _{\rm{s}}}}}, $ | (22) |
式中:ωD为模型E实际荷载-位移滞回曲线的面积,ωs为模型E的弹性应变能.
由于加载频率对模型荷载-位移滞回曲线的影响较小,因此加载频率对模型E等效刚度和等效阻尼比的影响较小.限于篇幅,本文仅给出加载频率为0.2 Hz时,模型E的等效刚度和等效阻尼比的计算结果.表 3为模型E等效刚度与等效阻尼比的简化模型分析结果与试验结果的比较,由表 3可知:
| 表 3 等效刚度Kv与等效阻尼比ζV Tab. 3 Equivalent stiffness Kv and equivalent damping ratio ζV |
1) 模型E等效刚度及等效阻尼比的简化模型分析结果与试验结果比较接近,两者误差在8%以内.
2) 随着加载预压位移的增大,模型E中的库仑摩擦力逐渐增大,进而导致模型E等效刚度的模拟值和试验值均逐渐增大.
3) 随着加载预压位移的增大,模拟与试验所得模型E荷载-位移滞回曲线的饱满度均逐渐增大,进而使得模型E等效阻尼比的模拟值和试验值均逐渐增大.
4) 随着动荷载幅值的增大,模拟与试验所得模型E荷载-位移滞回曲线的饱满度均逐渐减小,不对称性均逐渐增大,进而导致模型E等效刚度与等效阻尼比的模拟值和试验值均逐渐减小.
5 结论1) OO恢复力模型具有典型的非对称性特征,摩擦力对其恢复力特性影响较大.
2) OO恢复力模型能够有效对DSI装置的力学行为进行模拟.竖向往复荷载作用下,DSI装置模拟与试验的荷载-位移滞回曲线特征相似,等效刚度及等效阻尼比的模拟计算值与试验值相近.
3) 在竖向往复荷载作用下,随着动荷载幅值的增加,DSI装置的荷载-位移滞回曲线饱满度逐渐减小,因加、卸载刚度不同呈明显不对称性形状;随着加载预压位移的增加,DSI装置的荷载-位移滞回曲线趋于饱满,表明其耗能能力随着加载预压位移的增大逐渐增强.
| [1] |
ZHENG Enlai, JIA Fang, ZHOU Xinlong. Energy-based method for nonlinear characteristics analysis of Belleville springs[J]. Thin-Walled Structures, 2014, 79(2): 52. DOI:10.1016/j.tws.2014.01.025 |
| [2] |
张玉敏, 苏幼坡, 梁军, 等. 碟形弹簧竖向减震装置的研究[J]. 哈尔滨工业大学学报, 2008, 37(12): 1678. ZHANG Yumin, SU Youpo, LIANG Jun, et al. A study on vertical seismic isolation system by disc spring[J]. Journal of Harbin Institute of Technology, 2008, 37(12): 1678. |
| [3] |
JIA Fang, XU Fengyu. Combined vibration isolator of disc springs for closed high-speed precision press:Design and experiments[J]. Transactions of the Canadian Society for Mechanical Engineering, 2014, 38(4): 465. DOI:10.1139/tcsme-2014-0031 |
| [4] |
JIA Fang, ZHANG Fancheng. Mechanical properties of disc-spring vibration isolators based on boundary friction[J]. Journal of Southeast University (English Edition), 2014, 30(1): 39. DOI:10.3969/j.issn.1003-7985.2014.01.008 |
| [5] |
OZAKI S, TSUDA K, TOMINAGA J. Analyses of static and dynamic behavior of coned disc springs:Effects of friction boundaries[J]. Thin-Walled Structures, 2012, 59(4): 132. DOI:10.1016/j.tws.2012.06.001 |
| [6] |
CURTI G, MONTANINI R. On the influence of friction in the calculation of conical disc springs[J]. Journal of Mechanical Design, 1999, 121(4): 217. DOI:10.1115/1.2829508 |
| [7] |
PEDERSEN N L, PEDERSEN P. Stiffness and design for strength of trapezoidal Belleville springs[J]. Journal of Strain Analysis for Engineering Design, 2011, 46(8): 825. DOI:10.1177/0309324711414337 |
| [8] |
KARAKAYA S. Investigation of hybrid and different cross-section composite disc springs using finite element method[J]. Transactions of the Canadian Society for Mechanical Engineering, 2012, 36(4): 399. DOI:10.1139/tcsme-2012-0028 |
| [9] |
邢佶慧, 黄河, 张家云, 等. 碟形弹簧力学性能研究[J]. 振动与冲击, 2015, 34(22): 167. XING Jihui, HUANG He, ZHANG Jiayun, et al. Mechanical properties of disc springs[J]. Journal of Vibration and Shock, 2015, 34(22): 167. DOI:10.13465/j.cnki.jvs.2015.22.029 |
| [10] |
王维, 李爱群, 周德恒, 等. 新型三维多功能隔振支座设计及其隔振分析[J]. 东南大学学报(自然科学版), 2014, 44(4): 787. WANG Wei, LI Aiqun, ZHOU Deheng, et al. Design of novel three dimension multifunctional isolation bearing and its isolation behavior analysis[J]. Journal of Southeast University (Natural Science Edition), 2014, 44(4): 787. DOI:10.3969/j.issn.1001-0505.2014.04.019 |
| [11] |
赵亚敏, 苏经宇, 周锡元, 等. 碟形弹簧竖向隔震结构振动台试验及数值模拟研究[J]. 建筑结构学报, 2008, 29(6): 99. ZHAO Yamin, SU Jingyu, ZHOU Xiyuan, et al. Shaking table test and numerical analysis of vertical-isolated building model with combined disc spring bearing[J]. Journal of Building Structures, 2008, 29(6): 99. DOI:10.3321/j.issn:1000-6869.2008.06.014 |
| [12] |
XU Longhe, FAN Xiaowei, LI Zhongxian. Cyclic behavior and failure mechanism of self-centering energy dissipation braces with pre-pressed combination disc springs[J]. Earthquake Engineering & Structural Dynamics, 2017, 46: 1065. DOI:10.1002/eqe.2844 |
| [13] |
XU Longhe, FAN Xiaowei, LI Zhongxian. Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace[J]. Engineering Structures, 2016, 127: 49. DOI:10.1016/j.engstruct.2016.08.043 |
| [14] |
碟形弹簧: GB/T 1972-2005[S].北京: 中国标准出版社, 2005 Disc spring: GB/T 1972-2005[S]. Beijing: Standards Press of China, 2005 |
| [15] |
Dimensions and quality of conical disc springs: DIN 2093: 2013[S]. Berlin: German Institute for Standardization, 2013
|
 2019, Vol. 51
2019, Vol. 51


