风荷载对于建筑覆面安全性与经济性有重要作用,目前通用的覆面抗风设计方法基于无事故性损坏的假定.然而大量建筑覆面在强风暴下损坏的实际案例表明,风致损坏往往与突发事故有关,且具有不可忽略的连锁损坏特点.建筑覆面连锁损坏是由某个局部区域的小面积损坏(例如窗户开启或风掷物导致覆面开孔)引发建筑气动特性的极大改变,造成设计风压远小于实际风压,最终导致大面积覆面损坏的现象.图 1为美国New Orleans市某建筑物覆面在Katrina台风期间破坏的真实情况.

|
(图片来源 http://news.nationalgeographic.com) 图 1 美国新奥尔良某建筑覆面的风致连锁损坏 Fig. 1 Cascading damage of building cladding, New Orleans |
文献[1-2]很早便意识到了风致内压的作用以及风致破坏的重要性,文献[3]研究了建筑迎风墙面多开孔情况下的风致内压响应动力特性,文献[4-8]则在失效概率分析以及可靠度评估方面进行了研究.但上述研究主要以低矮建筑为主,且未考虑将建筑覆面在强风下是否开孔作为一概率事件.
建筑覆面的抗风设计原则上是一种概率设计,通常采用50 a或100 a回归期参考风压,对应覆面最大设计风压的年出现概率分别为2%或1%.然而事故性损坏会造成实际风压明显增大,且很可能会超过由规范计算或风洞试验所得的参考风压.对此,本文提出建筑覆面风致连锁损坏概率的风险评估方法,通过分析无事故性损坏与不同程度事故性损坏下的覆面风压并考虑风速风向联合分布概率与建筑覆面事故性损坏概率,为评估覆面的连锁损坏概率风险提供参考.
1 连锁损坏的机理与损坏模式建筑物覆面设计风压包括风直接引起的外压与建筑物内压(称为净风压).强风时的内压主要由外压的渗透与泄露造成,所以内压的大小往往与建筑物密闭性有关,同时受建筑物内部分隔影响,局部小空间与开敞式大空间内的内风压气动特性有很大不同.
在覆面抗风设计中,通常需要根据建筑物的覆面设计(例如是否为全封闭的玻璃幕墙,是否有可开启窗户以及可开启窗户的具体位置等)假设建筑物的密闭性等级(例如封闭式或某一指定的开洞率),然后确定相应的内压.在大部分情况下,封闭式建筑物的内压远小于外压.
但在以下3种典型随机事故下,上述覆面抗风设计的基本假定将不再成立:
1) 由于人为疏忽或机械故障,强风时未能全部关闭窗户,造成事实上的建筑局部开洞.
2) 由于风掷物(例如临近建筑物上被吹落的物体,松动的构件或广告牌等)造成建筑覆面局部损坏,导致局部开洞状态.
3) 由于设计或施工中的某些原因,某处幕墙在强风下出现局部损坏甚至脱落,从而造成建筑覆面局部开洞状态.除了可能的施工质量问题外,在幕墙设计或风洞试验中不适当地忽略了面积很小但局部风压很高的区域(通常称为“风压热点”)也可能是原因之一.
事故性的局部损坏将极大改变内压并可能使未损坏部分的覆面净压大大提高.需要注意的是,当局部损坏发生时,损坏处的外压并不能立即转化为内压,而是需要一定的反应时间.根据质量守恒原理,当某处发生局部损坏后,外压转化为内压的反应时间τ[9]为
| $ \tau = \frac{{\sqrt {{\rho _{\rm{a}}}} }}{{\gamma k{p_0}}}\left( {\frac{{{V_0}}}{A}\sqrt {2\Delta p} } \right), $ | (1) |
式中:ρa为空气密度,γ为空气比热比,k为与开孔处流量有关的常数,p0为大气压力,V0为室内空间体积,A为局部损坏面积,Δp为室内外压差.
如果建筑物迎风面与背风面上均有损坏发生,则两处外压转化为内压所需的反应时间[9]为
| $ \tau = \frac{{\sqrt {{\rho _{\rm{a}}}} }}{{\gamma k{p_0}}}\left( {\frac{{{V_0}{A_{\rm{w}}}{A_1}}}{{{{\left( {A_{\rm{w}}^2 + A_1^2} \right)}^{3/2}}}}} \right)\sqrt {2\Delta {p_{{\rm{w}}1}}} , $ | (2) |
式中:Aw为迎风面损坏面积,A1为背风面损坏面积,Δpw1为迎风面与背风面压差.
由此可见,如果损坏面积相对于室内空间很小,则需要较长的反应时间,造成外风压中只有平均值与低频部分能有效转化为内压.相反如果损坏面积相对于室内空间较大,则反应时间很短,造成大部分外风压都能迅速转化为内压.
在具体评估由局部损坏造成的覆面连锁损坏的概率时,需要根据实际情况考虑多种损坏模式.以图 2(a)为例,当建筑角部设置相邻可开启窗户时,如果强风时#1窗户未关闭,则#1处的正风压会进入该楼角单元并使得#2窗户上向外的负风压大大增加.反之,如果强风时#2窗户未关闭,#1窗户上向内的正风压也会大大增加.图 2(b)表示当关注点与未关闭窗户在同一单元内同一立面上时,却可能使净风压有所降低.

|
图 2 假定局部损坏位置 Fig. 2 Schematic diagram of assumed local damage |
由此可见由局部损坏造成的对其余覆面风压的影响是一个复杂的多因素事件.为了能从概率的角度把握局部损坏事件对覆面设计风荷载的影响,本文建立了如下所述的连锁损坏概率分析方法.
2 连锁损坏的风险概率分析建筑物覆面上某一测点的外风压时程可表示为
| $ {p_j}\left( {{l_j}, t} \right) = {\bar p_j}\left( {{l_j}} \right) + {\tilde p_j}\left( {{l_j}, t} \right), $ | (3) |
式中:lj为测点j的位置坐标,pj为测点j的风压平均值,
工程设计中主要关心峰值风压,一般表示为
| $ {\hat p_j} = {\bar p_j} \pm {g_ \pm }{\sigma _j}, $ | (4) |
式中:正负号代表计算峰值正压与峰值负压,σj为测点j的脉动风压均方差,g±为对应峰值正压与峰值负压的峰值系数.
如果与测点j处于同一内空间的某处k出现局部损坏,则由此造成的测点j处的净风压峰值表示为
| $ \begin{array}{l} {{\hat p}_j} = \left( {{{\bar p}_j} - {{\bar p}_k}} \right) \pm {g_ \pm }{\sigma _{j - k}} = \left( {{{\bar p}_j} - {{\bar p}_k}} \right) \pm \\ \;\;\;\;\;\;\;\;\;\;\;{g_ \pm }{\sigma _j}\sqrt {1 + \left( {\frac{{\sigma _k^*}}{{{\sigma _j}}}} \right) - 2{C_{jk}}\left( {\frac{{\sigma _k^*}}{{{\sigma _j}}}} \right)} , \end{array} $ | (5) |
式中:Cjk为测点j和测点k的脉动风压相关系数,σj-k为测点j和测点k的脉动风压差值的均方差,σk*为考虑反应时间后对测点k的脉动风压进行折减后的均方差.
目前实际工程中主要采用规范计算或是风洞试验确定参考风压,假定内压系数,忽略了事故性的局部损坏有可能带来的连锁损坏的概率.本文提出的连锁损坏概率分析方法基于风洞试验数据,采用时程分析方法直接求算局部损坏对周围覆面风压的影响,然后采用超越概率方法计算考虑发生连锁损坏概率后的回归期覆面设计风压.图 3为该方法计算流程.

|
图 3 回归期设计风压计算流程 Fig. 3 Flow chart of design wind pressure calculations |
具体计算详述如下(参见各框图左侧编号):
a) 假设由风洞试验得到某建筑物上共N个测点的外风压数据,依次计算各测点的风压系数Cp(定义为测点风压与参考风压之比)并将其时程分解为平均值和脉动值.计算中的测点以下标j表示.
b) 估计无覆面损坏前提下的基本内压系数.一般假定为封闭建筑,参照规范取值.
c) 假设与j测点关联的有n个测点,每个关联测点以下标k表示.关联是指如果在关联测点位置发生覆面开孔,将会影响测点j处的净压计算.将关联测点的风压系数时程也分解成平均值和脉动值.
d) 根据式(1)估计反应时间τ,并据此对关联测点的脉动风压系数时程进行数字低通滤波(LPF)处理.其目的是为了考虑外压转化为内压的反应时间.如果损坏造成的相对开孔较小,则反应时间较长,只有风压的平均值与低频部分能转化为内压.如果损坏造成的相对开孔较大,则反应时间较短,内压与大部分外风压相等.由此得到多种损坏模式.
e) 根据基本内压系数计算测点j处的净压系数,以Cpj0表示.
f) 根据关联测点k处损坏造成的内压变化计算测点j处的净压,以Cpjk(其中k=1…n)表示.
g & h)采用最佳线性无偏估计方法分别计算Cpj0和Cpjk中脉动分量的正向峰值系数与负向峰值系数.这里定义指向覆面的为正向,指离覆面的为负向.
i & j)采用超越概率分析方法分别计算pj0和pjk与各自出现概率的函数关系.pj0意为无覆面损坏前提下测点位置j的净风压,pjk意为关联位置k发生覆面开孔后测点位置j的净风压.Pj0与pjk中又包含了峰值正压与峰值负压.值得指出的是上述Pj0和Pjk是参考风速与风向角的函数,所以如果给定pj0或pjk某一风压值,在不同风向角下达到该风压的风速有所不同.由此可计算出某一位置在不同风向角下达到某一给定风压值所需的风速大小,并将此定义为该给定风压值的风速边界线Us,如图 4所示.风速边界线代表了某一位置风压对风向角的敏感程度.若实际风速超越了风速边界线,则相应测点上的实际风压会大于该风速边界线所对应的给定风压值.从而将给定重现期下参考风压的问题归结为超越概率问题.

|
图 4 超越概率分析方法 Fig. 4 Upcrossing method |
显然,对同样风压值每个测点的风速边界线有所不同.采用Weibull模型描述当地风速风向联合概率分布时,某指定风压的出现概率可借助相应的风速边界线计算得到[10]:
| $ \begin{array}{*{35}{l}} \text{Prob}\left( {{{\hat{p}}}_{j}} \right)=\sum\limits_{i=1}^{{{N}_{\text{w}}}}{\frac{1}{2}}|{{{\bar{\dot{U}}}}_{sj}}{{|}_{i}}\sqrt{1+\frac{|{{{\bar{\dot{\theta }}}}_{sj}}{{|}_{i}}}{{{\left| {{{\bar{\dot{U}}}}_{sj}} \right|}_{i}}}\left( \frac{\text{d}{{U}_{sj}}}{\text{d}\theta } \right)\times } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left[ \frac{{{A}_{i}}{{K}_{i}}}{{{C}_{i}}}{{\left( {{U}_{sj}}/{{C}_{i}} \right)}^{{{K}_{i}}-1}}\exp \left( -{{\left( {{U}_{sj}}/{{C}_{i}} \right)}^{{{K}_{i}}}} \right) \right], \\ \end{array} $ | (6) |
式中:Ai、Ci、Ki为Weibull分布系数,NW为风向角数目,Usj为指定风压
| $ {\mathop{\rm Prob}\nolimits} \left( {{{\hat p}_j}} \right) = \Gamma \left( {{{\hat p}_j}} \right), $ | (7) |
式中Γ代表概率函数.
k) 可以合理假定本文所述事故性损坏是突发性离散事件,损坏事件之间没有相关性.采用Poisson模型描述覆面损坏事件的概率函数,即事件发生x次的概率为
| $ {\mathop{\rm Prob}\nolimits} (x) = \frac{{{\lambda ^x}}}{{x!}}\exp ( - \lambda ), $ | (8) |
式中λ是事故平均发生率.
因此给定时间内某关联测点位置k至少出现一次事故的概率为
| $ {P_{{\rm{D}}k}} = 1 - \exp ( - \lambda ), $ | (9) |
l) 计算考虑事故不发生概率与各种不同事故发生概率后某指定风压值的出现总概率
| $ \begin{array}{l} {\mathop{\rm Prob}\nolimits} \left( {{{\hat p}_j}} \right) = \prod\limits_{k = 1}^n {{\Gamma _0}} \left( {{{\hat p}_j}} \right)\left( {1 - {P_{{\rm{D}}k}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^n {{\Gamma _k}} \left( {{{\hat p}_j}} \right){P_{{\rm{D}}k}}, \end{array} $ | (10) |
上式中右端第一项代表与某位置关联的所有测点没有一处发生损坏情况下某指定净风压的出现概率;右端第二项则为不同损坏模式下该指定风压值的出现概率.某指定风压值的出现总概率为不发生覆面损坏情况下该风压值的出现概率与发生连锁损坏情况下该风压值的出现概率之和.
m) 由于上一步得到的结果为单调函数,所以可通过逆运算得到指定出现概率下的风压值.相应的回归期为出现概率的倒数.
通过上述计算可以得到考虑事故性损坏风险后的覆面设计风压,并且可计算在忽略事故性损坏风险前提下得到的覆面设计风压所对应的实际回归期.
这一方法解决了理论计算的问题,但在实际应用中可能遭遇具体参数取值上的困难.由于覆面损坏造成的实际内压变化涉及到包括室内空间及其渗透率等很多复杂细节,损坏点外压与内压之间的详细关系需要借助有针对性的个案研究.此外由于缺乏统计资料,一般难以确切估计事故性覆面损坏的概率(即Poisson分布中的λ系数).所以对大多数工程问题,连锁损坏的风险概率分析需要结合界定性评估方法.下述案例研究将给出界定性评估具体做法.界定性评估的意义在于3个方面:1)对覆面损坏可能造成围护结构设计风压增大的范围有一个基本界定;2)辨识风致连锁损坏风险较大的区域以便采取必要的设计措施;3)评估设计风压对事故概率的敏感度,由此作为评估物业管理重要性的参考.
3 案例研究以浙江某办公大楼的风洞试验数据为例进行分析.大楼建筑总高度为216 m,以1: 300几何缩尺制作的测压模型(图 5)在浙江大学ZD-1边界层风洞实验室中完成了同步测压试验.试验中模型楼顶高度的试验风速为8.6 m/s.采样频率312.5 Hz,采样时长90 s.试验风向角以正北为0°,等间隔测试了36个风向角下的覆面外风压.建筑物北立面对应风向角20°.图 6(a)给出沿建筑竖直向的测压点分布,图 6(b)给出典型楼层沿建筑水平向的测压点分布.

|
图 5 1: 300风洞测压模型 Fig. 5 1: 300 scale wind tunnel testing model |

|
图 6 风压测点布置 Fig. 6 Layout of pressure taps |
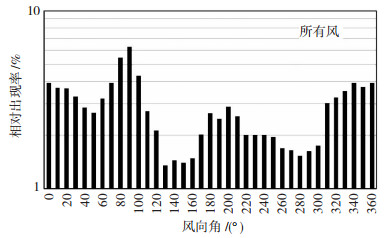
项目所在地50 a回归期基本风压为0.45 kN/m2.根据历史风气候资料统计分析得到风速风向联合概率分布.作为示例,图 7给出不计风速大小的风在各风向角的相对出现率.
|
图 7 风速风向联合概率分布 Fig. 7 Joint-probability of wind velocity and wind direction |
为了从整体上把握事故性覆面局部损坏对覆面风压的影响,采用界定性评估方法,考虑以下3种极端工况:
1) 无损坏:建筑物在强风情况下不发生覆面损坏.
2) 小面积损坏:损坏面积远小于建筑内空间以致由局部损坏造成的内压与损坏处的外压平均值基本一致.
3) 大面积损坏:由局部损坏造成的内压与损坏处的总外压基本一致.
取V0/A为自变量,由式(1)可初步估算某处发生局部损坏后,外压转化为内压的反应时间τ.其中ρa取1.2 kg/m3,γ取1.4,k取0.6,p0取101.3 kPa,Δp为室内外压差.又因为外风压系数
需要说明的是本文给出的开孔面积仅为示例,在应用到某一具体建筑物时需根据室内空间体积及开孔面积进行更为精确的计算.另外对于大开孔和小开孔情况的界定,目前尚未见到针对有内部分隔的高层建筑开孔率的理论或试验分析,本文仅根据相对反应时间的长短对开孔率进行了初步判断,具体界限仍有待进一步研究.
在不考虑覆面损坏工况时的建筑内压按封闭式建筑考虑,根据中国建筑规范取±0.2的内压系数.在小面积损坏及大面积损坏情况下建筑内压则通过对相应点的同步测压数据得以估计,因而所涉及方法在进行风洞试验时仍可采用密闭建筑物.
在风洞试验数据处理中采用Cook等[11]提出的最佳线性无偏估计(best linear unbiased estimate,BLUE)方法计算风压极值,以考虑负风压的非高斯特性[12-14], 计算公式为
| $ \left\{ \begin{array}{l} {C_{p.\max }} = {C_{p.{\rm{ mean }}}} + {\mu _{\max }} + 0.5772/{\alpha _{\max }}, \\ {C_{p.\min }} = {C_{p.{\rm{ mean }}}} - {\mu _{\min }} - 0.5772/{\alpha _{\min }}. \end{array} \right. $ | (11) |
式中μ为模(mode)参数,1/α为散度(dispersion)参数,可按如下步骤求得:
1) 将风洞试验得到的风压系数时程数据Cp(t)等分为10段(每段长度相当于足尺10 min),取每段数据最大值Cp.max, i与最小值Cp.min, i按绝对值大小重新排列.
2) 由下式求出模参数与散度参数:
| $ \left\{ \begin{array}{l} {\mu _{\max }} = \sum\limits_{i = 1}^N {{a_i}} {C_{p.\max , i}}, \\ {\mu _{\min }} = \sum\limits_{i = 1}^N {{a_i}} \left| {{C_{p.\min , i}}} \right|. \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} 1/{\alpha _{\max }} = \sum\limits_{i = 1}^N {{b_i}} {C_{p.\max , i}}, \\ 1/{\alpha _{\min }} = \sum\limits_{i = 1}^N {{b_i}} \left| {{C_{p.\min , i}}} \right|. \end{array} \right. $ | (13) |
| 表 1 系数a与b取值 Tab. 1 Value of factors a and b |
图 8给出典型楼层中部区域相邻幕墙上无损坏、小面积损坏、大面积损坏3种模式下关注区的覆面净风压系数随风向角的变化.图 9给出楼角区域的事故性损坏对相邻覆面净风压的影响.图中Cp.max为峰值正风压系数,Cp.min为峰值负风压系数.

|
图 8 中部损坏造成覆面净压的变化 Fig. 8 Variation of facade net pressure due to damage at middle zone |

|
图 9 角部损坏造成覆面净压的变化 Fig. 9 Variation of facade net pressure due to damage at corner zone |
可以看出,在大多数风向角下中部损坏对同一立面上的风压没有明显不利影响, 由于损坏处风压与关注点风压基本同号,反而有一定降低作用,而角部损坏对相邻覆面净压的影响较为显著,特别是关注点的正压.对于中部损坏,风向角290°附近由于损坏处负风压明显大于关注点,因而当损坏发生时会在关注点产生很大的正向净压.对于角部损坏,无损坏时关注点最大正压发生在170°左右,相邻楼角处的损坏不但使最大正压转移到190°左右,而且量值上增加48%~100%,负压的增量则为12%~19%.这一现象主要由两方面原因造成:其一是楼角区域的正外压在数值上远小于负外压,所以由负压区破损造成正压增加远比正压区破损造成负压增加明显;其二是负压区的湍流成分较多,所以由负压区破损造成的正压增加对破损面积大小较为敏感.
采用超越概率计算公式,首先设定不同的风压等级(本例中取-5.0 kPa到5.0 kPa,以0.1 kPa为间隔)将所得结果结合风气候概率统计模型进行超越概率分析后,可以得到某一位置在不同损坏模式下该风压等级的出现概率,由此得到不同年出现概率下3种典型损坏模式的最大覆面净风压.图 10(a)和图 10(b)给出典型中间区域和典型楼角区域在不同年出现概率下的最大风压.

|
图 10 不同损坏模式下的净风压峰值 Fig. 10 Peak net pressures for various damage configurations |
图 10再次说明中部覆面损坏对同一面上的风压没有明显的不利影响,而角部覆面损坏则会明显增大相邻角部的正风压值,对相邻角部的负风压值也会有一定的不利影响.
5 概率风险评估模型在这些结果基础上,将事故性覆面损坏作为一种概率事件,进一步求算相应的覆面设计风荷载.
假设统计期限10 a内某类建筑(例如某小区)遭遇强风时至少有一扇窗户未关闭的事件高达20起,则认为式(8)中事故平均发生率λ为2(=20/10).由此可得至少出现一次损坏的概率PDk为86%,而不出现损坏的概率仅为14%.另外考虑到小面积损坏可能更易发生,故假设小面积损坏与大面积损坏事件发生概率之比约为2: 1.
作为界定性评估,假定事故平均发生率λ为0~3,分析比较4种工况.
| 表 2 事故发生概率 Tab. 2 Accident probability |
同样以典型中间区域和典型楼角区域为例,根据式(10)计算得到上述4种工况下最大净风压与回归期的关系,见图 11.

|
图 11 不同事故发生率假定下的回归期设计风压 Fig. 11 Return period wind pressures for various accident cases |
对每个风压测点都进行类似上述的计算,可以得到不同事故概率假定下不同区域的回归期设计风压.将由此得到的设计风压(工况1至工况3)与不考虑覆面损坏的设计风压(工况0)之比定义为设计风压增大率,可得到对覆面事故性损坏风险的整体评估.图 12分4种情况给出针对本案例50 a回归期设计风压的增大率.

|
图 12 覆面事故性损坏引起的设计风压增大率 Fig. 12 Increment of design wind pressure due to accidental facade damage |
可看出,对案例中的高层建筑,建筑立面中间区域的事故性损坏对中间区域的覆面风压不会产生不利影响,但建筑楼角区域的事故性损坏则会对邻近楼角区域的覆面风压造成不利后果,导致设计正风压增大至1.67倍,设计负风压增大至1.19倍.
本文建立方法能用于评估建筑表面事故性损坏对覆面设计风荷载的影响,是精细化设计的一个重要方面.同时也有助于发现对局部损坏较为敏感的区域,以便在设计中采取必要措施控制事故性损坏,从而提高设计的可靠性.
需要指出,图 12所描述的事故性损坏对覆面风压的影响仅具有一般性的代表意义.建筑体型与室内设计等因素都会极大改变这一结果的具体大小.所以在实际工程中,必须结合具体的设计细节进行风险评估才能得到有针对性的结果.
6 结语提出一种考虑建筑覆面风致连锁损坏的概率风险评估方法,可计算在设计回归期下,事故性覆面局部损坏对覆面设计风荷载可能造成的影响,并辨识对局部损坏较为敏感的区域,以便采取必要措施控制事故性损坏的后果.该方法的特点是能够较为全面地考虑影响覆面设计风荷载的各种因素,不但包括建筑体型与风场因素,而且能详细考虑风气候中风速风向的联合统计特性以及建筑内部空间分割的特点.
采用该方法分析了一栋典型的办公建筑,结果表明楼角区域的正风压对覆面局部损坏最为敏感,中间区域的事故性损坏对中间单元的幕墙风压则影响较小.
事故性损坏对覆面设计风压的影响取决于很多因素,因而具有很大的个案性.本文方法为解决这类工程问题提供了有力工具.
| [1] |
唐锦春, 孙炳楠, 楼文娟, 等. 屋面风荷载及风致破坏机理[J]. 建筑结构学报, 2000, 21(4): 39. TANG Jinchun, SUN Bingnan, LOU Wenjuan, et al. Wind load on roof structures and mechanism of wind-induced damages[J]. Journal of Building Structures, 2000, 21(4): 39. DOI:10.3321/j.issn:1000-6869.2000.04.006 |
| [2] |
孙炳楠, 卢旦, 楼文娟. 风致内压及其对屋盖结构的作用研究现状评述[J]. 建筑科学与工程学报, 2005, 22(1): 76. SUN Bingnan, LU Dan, LOU Wenjuan. Review of wind-induced internal pressure and its effects on roof structures[J]. Journal of Architecture and Civil Engineering, 2005, 22(1): 76. DOI:10.3321/j.issn:1673-2049.2005.01.012 |
| [3] |
徐海巍, 余世策, 楼文娟. 迎风墙面多开孔结构风致内压的试验研究[J]. 振动与冲击, 2014, 33(15): 82. XU Haiwei, YU Shice, LOU Wenjuan. Tests for wind-induced internal pressure of a building with multiple openings on its windward wall[J]. Journal of Vibration and Shock, 2014, 33(15): 82. |
| [4] |
IRWIN P A, SIFTON V L. Risk considerations for internal pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 77/78: 715. DOI:10.1016/s0167-6105(98)00186-x |
| [5] |
OLARI G. Mathematical model to predict 3-D wind loading on buildings[J]. Journal of Engineering Mechanics, 1985, 111(2): 254. DOI:10.1061/(asce)0733-9399(1985)111:2(254) |
| [6] |
ZHANG S, NISHIJIMA K, MARUYAMA T. Climate model-based probabilistic assessment of wind risk for residential buildings under projected future climate[J]. Civil Engineering and Environmental Systems, 2014, 31(2): 98. DOI:10.1080/10286608.2014.912642 |
| [7] |
VANMARCKE E, LIN N. Quantitative risk analysis of damage to structures during windstorms: random field and system reliability aspects[C]//International Symposium on Uncertainty Modeling and Analysis and Management. Hyattsville, Maryland: [s.n.], 2011: 11. DOI: 10.1061/41170(400)2
|
| [8] |
BJARNADOTTIR S, LI Y, STEWART M G. Hurricane risk assessment of power distribution poles considering impacts of a changing climate[J]. Journal of Infrastructure Systems, 2013, 19(1): 12. DOI:10.1061/(asce)is.1943-555x.0000108 |
| [9] |
HOLMES J. Wind loading of structures[M]. New York: Spon Press, 2001: 137.
|
| [10] |
IRWIN P A. Pressure model techniques for cladding loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1/2/3): 73. |
| [11] |
COOK N J, MAYNE J R. A refined working approach to the assessment of wind loads for equivalent static design[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1979, 4(2): 149. DOI:10.1016/0167-6105(79)90043-6 |
| [12] |
楼文娟. 超高层建筑脉动风压的非高斯特性[J]. 浙江大学学报(工学版), 2011, 45(4): 671. LOU Wenjuan. Non-Gaussian feature of wind-induced pressure on super-tall building[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(4): 671. DOI:10.3785/j.issn.1008-973X.2011.04.014 |
| [13] |
全涌, 顾明, 陈斌, 等. 非高斯风压的极值计算方法[J]. 力学学报, 2010, 42(3): 560. QUAN Yong, GU Ming, CHEN Bin, et al. Study on the extreme value estimating method of non-Gaussian wind pressure[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 560. DOI:10.6052/0459-1879-2010-3-2009-062 |
| [14] |
双妙, 宋波. 风荷载的非高斯性对风机结构疲劳损伤的影响[J]. 哈尔滨工业大学学报, 2017, 49(12): 152. SHUANG Miao, SONG Bo. Influence of non-Gaussian characteristics of wind load on fatigue damage of wind turbine[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 152. DOI:10.11918/j.issn.0367-6234.201704091 |
| [15] |
COOK N J. Designer's guide to wind loading of building structures Part 1:background, damage survey, wind data & structural classification[M]. London: Garston and Butterworths, 1985: 323.
|
 2019, Vol. 51
2019, Vol. 51


