2. 上海大学 风工程和气动控制研究中心,上海 200444
2. Wind Engineering and Aerodynamic Flow Control Research Center, Shanghai University, Shanghai 200444 China
多圆柱结构在工程中有广泛应用,如冷却塔群、多分裂导线、缆索承重桥并列索等.双圆柱结构是最简单的多圆柱类型,得到了广泛研究.由于双圆柱结构的干扰流态复杂,影响因素多样,尚有不少问题需要进一步研究[1].对于并列双圆柱,以往学者大多采用风洞试验研究其气动性能[1-5]和流场特性[5-8].研究表明[1],随着圆柱间距的增大,并列双圆柱的绕流场可分为单一钝体、偏向流和平行涡街三种流态.
偏向流流态是并列双圆柱的一种特殊现象,尽管来流和圆柱是对称的,但其绕流场和气动性能却呈现明显的不对称性.已有学者对偏向流特性进行了研究,但其确切的机理尚不清楚.Ishigai等[9]认为是Coanda效应引起了偏向流,但Miau等[10]通过试验证明其并非由Coanda效应引起.以往研究还发现,偏向流的偏转方向会间歇性地发生切换[11-12],具有很强的雷诺数效应[13].Brun等[13]发现,当雷诺数大于某一临界值时,自由剪切层失稳引起的Kelvin-Helmholtz涡及其本身的间歇性是造成间隙流偏向及其方向变化的主要原因,并且方向变化会随着雷诺数的增大变得更为频繁.值得注意的是,以往对偏向流流场的研究均是在较低雷诺数(Re<104)下进行的[14-15].由于圆柱绕流有强烈的雷诺数效应,高雷诺数下的流场特性很可能与低雷诺数下的不同.
最近几年,计算流体动力学(CFD)方法被用于研究并列双圆柱[16-18].CFD方法可同时得到绕流场和气动性能,便于研究气动性能与流场特性之间的关系.但已有的数值模拟研究大部分局限在低雷诺数(102~103)下[17-18].工程中的双圆柱结构大多工作在雷诺数大于105的环境中,因而有必要研究高雷诺数下的流场干扰机理.
本文以圆心间距比为P/D=1.1~4的并列双圆柱绕流为研究对象,采用大涡模拟方法在高雷诺数下(Re=1.4×105)研究了并列圆柱的表面风压系数、气动力系数和Strouhal数等气动性能随圆柱间距比的变化规律,研究了绕流场流态与圆柱气动性能的关系,特别是偏向流流态下的流场特性及其气动性能,进一步澄清了并列双圆柱气动干扰的流场作用机制.
1 计算模型和研究工况 1.1 控制方程和亚格子模型对湍流场进行数值模拟可以采用直接数值模拟(DNS)、雷诺平均法(RANS)和大涡模拟(LES)三种方法.当采用大涡模拟方法时,流场中的大尺度涡通过滤波后的Navier-Stokes方程直接求解,而小尺度涡则采用亚格子尺度模型(SGS)模拟.与直接数值模拟相比,大涡模拟可以节约计算机的资源;与雷诺平均法相比,大涡模拟方法能更好地模拟流场中的湍流旋涡,捕捉到更完善的流场脉动信息.因此,为了准确模拟并列双圆柱绕流场特性,本文采用大涡模拟方法进行研究.
经过滤波函数的滤波,可得到大尺度涡的不可压缩Navier-Stokes方程:
| $ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0, $ | (1) |
| $ \frac{{\partial {{\bar u}_i}}}{{\partial t}} + \frac{{\partial {{\bar u}_i}{{\bar u}_j}}}{{\partial {x_i}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + v\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{{\partial {\mathit{\boldsymbol{\tau }}_{ij}}}}{{\partial {x_j}}}. $ | (2) |
式中:ui为滤波后速度分量,ρ为流体密度,p滤波后压力,v为流体动力黏度,τij为亚格子应力张量.
本文的亚格子应力τij采用Smagorinsky-Lilly的亚格子尺度模型,具有以下形式:
| $ {\mathit{\boldsymbol{\tau }}_{ij}} - \frac{1}{3}{\mathit{\boldsymbol{\tau }}_{kk}}{\delta _{ij}} = - 2{v_t}{\bar S_{ij}}, $ | (3) |
| $ {\bar S_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right). $ | (4) |
式中vt是亚格子尺度的湍动黏度,
| $ {v_t} = \rho L_{\rm{s}}^2|\bar S| = {\left( {{C_{\rm{s}}}\Delta } \right)^2}|\bar S|, $ | (5) |
其中
| $ |\bar S| \equiv \sqrt {2{{\bar S}_{ij}}{{\bar S}_{ij}}} , $ | (6) |
| $ \Delta = {V^{1/3}}. $ | (7) |
式中Ls代表亚格子网格尺寸的最小长度,Cs是Smagorinsky常数,本文取0.1.
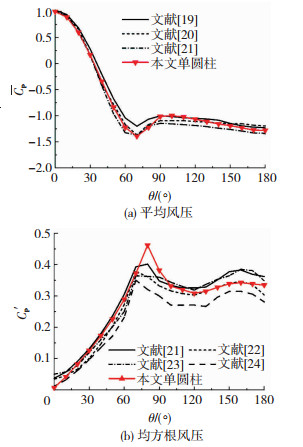
1.2 计算模型验证为进行网格独立性验证,首先针对单圆柱模型,比较了周向网格数、展向长度以及计算时间步长等计算参数对结果的影响.表 1将单圆柱模型的气动力系数和St数与文献风洞试验结果进行了比较,数值模拟结果与试验结果吻合良好.由工况Case1~Case3可见,随着周向网格数的增加,计算结果越接近于文献值;当周向网格数为400时,平均阻力系数、脉动升力系数和St数均与文献值吻合较好,故周向网格数取400.由工况Case4~Case6可见,随着无量纲时间步的减小,本文数值模拟结果逐渐接近文献值,故无量纲时间步取为0.005.对比工况Case3和Case6,展向长度的增加会使计算结果更靠近试验值,所以计算模型的展向长度取为2D.图 1为工况Case6得到的平均和脉动风压系数与文献中风洞试验结果的比较,本文的风压系数分布与文献结果吻合良好.因而,本文并列双圆柱绕流的计算模型和计算参数参考Case6.
| 表 1 单圆柱计算结果验证 Tab. 1 Comparison of results of a single circular cylinder |
|
图 1 单圆柱风压系数分布 Fig. 1 Pressure coefficient distribution of a single cylinder |
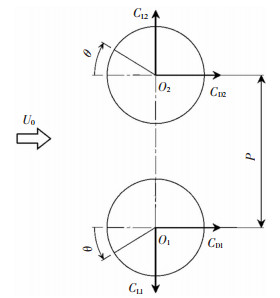
并列双圆柱计算模型见图 2.基于来流风速U0和圆柱直径D计算得到的雷诺数为Re=1.4×105.圆柱的中心间距为P,本文共计算了5种中心间距:P/D=1.1、1.2、1.5、2、3、4.规定两个圆柱的升力系数CL的正向见图 2,即排斥为正,吸引为负.圆柱表面位置角θ定义为:上侧圆柱以顺时针为正,下侧圆柱以逆时针为正.
|
图 2 计算模型示意 Fig. 2 Schematic diagram of the computational model |
计算域和局部平面网格见图 3.采用O型计算域,计算域直径为46D,计算模型的展向长度为2D,阻塞率为4.35%.计算域入口边界采用速度入口边界条件(velocity-inlet),出口边界采用自由出口边界条件(outflow),圆柱展向两端采用周期性边界条件(periodic),圆柱表面采用无滑移壁面条件(wall).

|
图 3 计算域及网格 Fig. 3 Computational domain and grid |
采用结构化网格,圆柱周向400个单元,径向180层单元,展向为20层单元;近壁面最小网格为0.000 1D,近壁面y+≈1;无量纲时间步Δt*为0.005 (Δt*= ΔtU0/D,其中Δt为实际计算时间步,U0为来流风速).计算模型总单元数为266万至334万不等.
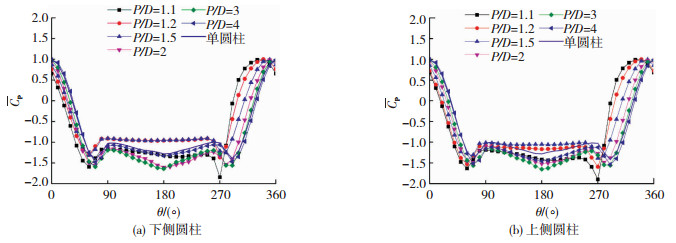
2 计算结果及分析 2.1 表面风压系数图 4、5为不同圆心间距下圆柱表面的平均风压系数和脉动风压系数图,图中也列出了单圆柱计算结果.由图 4可见,迎风侧的风压停滞点会随着间距变化发生偏移.当P/D=1.1时,风压停滞点在-25°左右.随着圆心间距的增大,风压停滞点的位置也越来越接近0°位置:当P/D=1.2时,风压停滞点位置为-20°;P/D=1.5时为-10°;P/D=2时为-9°;P/D=3和4时则接近于0°.并列圆柱背风侧(θ=90°~270°)的负压强度随着间距的增大变化剧烈.P/D=1.2和1.5时负压强度小于单圆柱,P/D=2和3时明显大于单圆柱.当P/D=1.1时,两个圆柱在θ=270°处(位于两个圆柱的间隙侧)有明显的强负压,风压系数在-1.9左右.当间距增大至P/D=4时,并列圆柱的平均风压逐渐接近于单圆柱.
|
图 4 表面平均风压系数 Fig. 4 Mean pressure coefficient distribution |
|
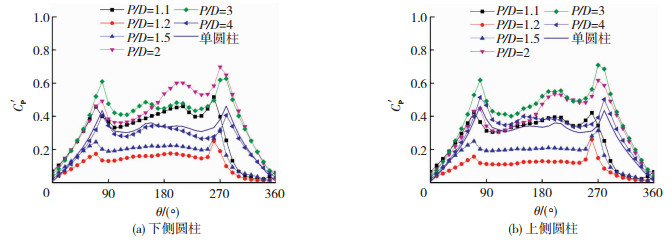
图 5 表面脉动风压系数 Fig. 5 RMS pressure coefficient distribution |
由图 5可见,随着间距增大,脉动风压系数变化剧烈.P/D=1.1时,背风侧脉动风压大于单圆柱,在θ=270°~360°的间隙侧则小于单圆柱;P/D=1.2和1.5的脉动风压系数总体上明显小于单圆柱;而P/D=2和3的脉动风压系数则明显大于单圆柱,圆柱间隙侧(θ=180°~360°)的脉动风压则远大于圆柱外侧(θ=0°~180°);随着间距比增加至P/D=4,两个圆柱的脉动风压分布均接近于单圆柱.
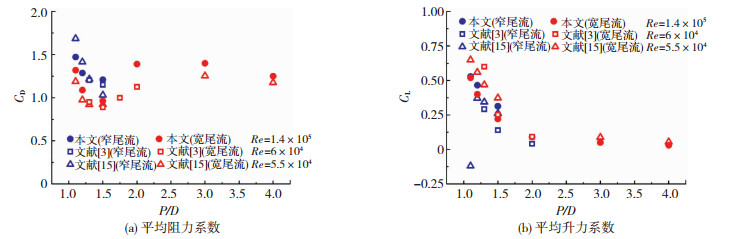
2.2 气动力系数 2.2.1 平均气动力图 6为并列圆柱的平均气动力系数与文献[3, 15]的结果进行比较,文献[3, 15]是在二维流场中得到的风洞试验结果.当间距比P/D在1.1~2时,并列圆柱会出现偏向流,两个圆柱的尾流出现一宽一窄现象,圆柱的平均气动力也会有差异.文献[15]研究表明:尾流较宽圆柱的平均阻力系数较小,而尾流较窄圆柱的阻力系数较大.为了与文献结果进行比较,本文也根据两个圆柱平均阻力系数的大小来区分尾流的宽窄.
|
图 6 气动力系数 Fig. 6 Aerodynamic coefficients |
由图 6可见,本文的结果与文献结果总体变化趋势相同.当P/D<2时,两个圆柱的阻力系数和升力系数均有一定的差异,即存在偏向流的现象;当P/D≥2时,两个圆柱的平均气动力基本相同.由图 6(a)可见,随着间距的增大,平均阻力系数在P/D=1.1~2之间会先减小后增大;而在P/D≥2之后则会逐渐减小并接近于单圆柱数值.对于平均升力系数,由图 6(b)可见,其数值会随着间距的增大逐渐减小,总体上表现为斥力.
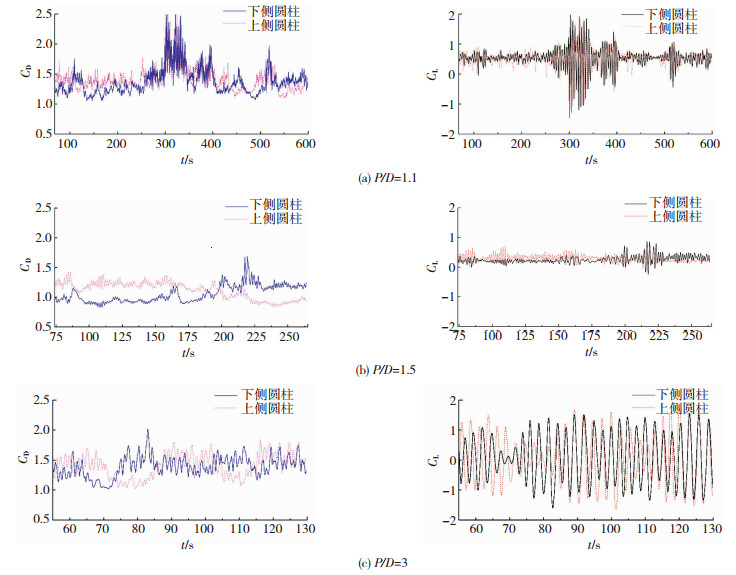
2.2.2 气动力时程图 7给出了P/D=1.1、1.5和3时并列圆柱的气动力系数时程曲线.由阻力系数时程(左侧图)可见,在3种间距下,两个圆柱阻力系数的大小均有交替变化的现象.如P/D=1.5时,在75~200 s上侧圆柱的阻力明显大于下侧圆柱,而在200 s之后则情况相反.随着间距的增大,阻力系数大小的交替变化越来越频繁,即偏向流现象会逐渐减弱.从升力系数时程(右侧图)可见,3种间距的升力波动幅度有很大差异,这说明3种间距的绕流流态不同.当P/D=1.2和1.5时,两个圆柱的升力波动幅度都很小,并且缺乏规律性;而当P/D≥2时,两个圆柱的升力波动幅度很大,并有很强的周期性.当P/D=1.5时,上、下侧圆柱的升力系数在200 s附近发生了突变,说明偏向流偏转方向的变化会引起气动力的突变.当P/D=1.1时,升力系数在300~400 s出现很大波动,升力系数时程呈现非稳态现象,这也说明P/D=1.1时并列双圆柱的流态会随时间发生变化.
|
图 7 并列双圆柱气动力系数时程(左侧:阻力;右侧:升力) Fig. 7 Time history of aerodynamic force coefficients of two side-by-side circular cylinders (Left: Drag; Right: Lift) |
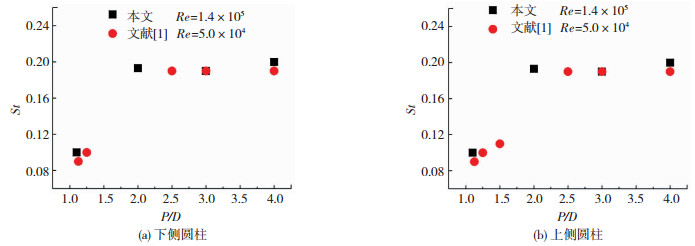
图 8为双圆柱随着圆心间距变化的Strouhal数(St=fD/U0,f为涡脱频率).由图 8可见,上下侧圆柱的St数值几乎相同.当P/D=1.1时,St数为0.1左右,约为单圆柱的1/2;当P/D=1.2和1.5时,没有明显的St数,当P/D≥2时,St数随着间距的增大没有明显变化,并接近单圆柱的值0.2.
|
图 8 斯托罗哈数 Fig. 8 Strouhal number |
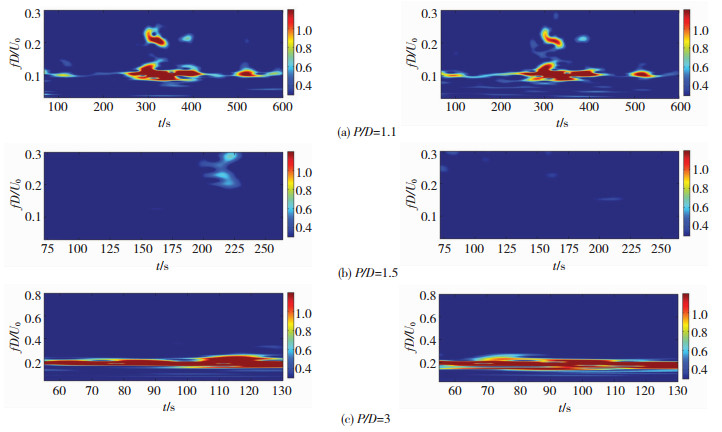
为了分析St数随时间的变化规律,本文采用Morlet小波作为基函数对升力系数时程进行小波谱分析.图 9给出了3种间距并列双圆柱升力系数时程的时频能量谱.从图 9可见,在同一间距比下,上下侧圆柱的时频图基本相同.当P/D=1.1时,在300~400 s间能量主要集中在fD/U0=0.1处,另外在fD/U0=0.2处能量也较大.当P/D=1.2和1.5时,时频能量谱中没有明显的能量集中.当P/D≥2时,能量集中在fD/U0=0.2左右,其数值与单圆柱绕流的St数接近.
|
图 9 下侧圆柱与上侧圆柱升力系数时频能量谱 Fig. 9 Wavelet power spectrum for the lift coefficients of the lower and upper cylinders |
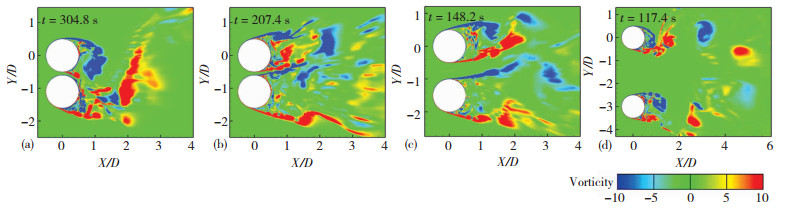
图 10为不同圆心间距下典型时刻(上侧圆柱升力达到波峰时刻)的瞬态涡量图.随着间距的变化,并列圆柱的流态结构会发生很大变化.当P/D=1.1时,并列双圆柱在不同的时刻会呈现出单一钝体(图 10(a))和偏向流(图 10(b))两种流态;对于单一钝体流态,两个圆柱如同一个钝体,一对旋涡会从上侧圆柱上表面和下侧圆柱下表面交替脱落,并在尾流中形成一个涡街.而对于偏向流流态,在图 10(b)所示时刻,在两个圆柱中间流过的间隙流会引起上侧圆柱的尾流变窄,而下侧圆柱的尾流变宽.
|
((a) P/D =1.1(单一钝体流态);(b) P/D =1.1(偏向流流态);(c) P/D =1.5;(d) P/D =3) 图 10 并列圆柱瞬时涡量图 Fig. 10 Instantaneous vorticity |
当P/D=1.2和1.5时,如图 10(c)所示,双圆柱呈现偏向流流态,但偏向的幅度较图 10(b)小;两个圆柱的4个剪切层在分离后均保持较为平顺的形状,即剪切层失稳并形成旋涡的位置离圆柱较远,因而尾流旋涡对圆柱气动力的周期性影响小,圆柱的脉动升力小,且升力功率谱没有明显的St数.
当P/D≥2时,偏向流现象随着间距增大逐渐消失,两个圆柱均有各自的旋涡脱落,形成两个平行的涡街.
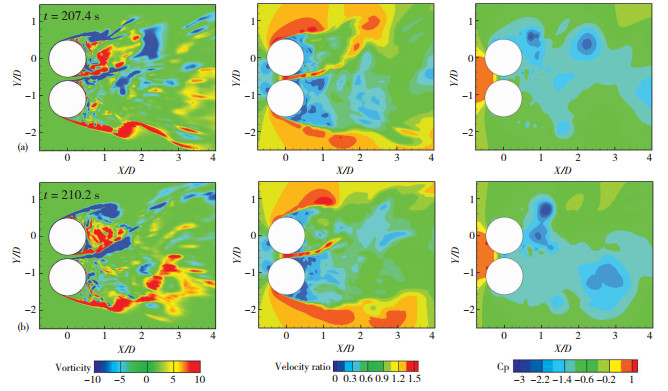
2.4.2 P/D=1.1流态分析当P/D=1.1时,并列双圆柱在不同的时刻会呈现出单一钝体和偏向流两种流态,为了进一步理解其流场特性及其对气动力的影响,图 11、12给出了这两种流态典型时刻的瞬态涡量图、瞬态风速图和瞬态风压场,两个典型时刻分别为上侧圆柱在一个升力周期内升力最大时刻和最小时刻.
|
图 11 P/D=1.1偏向流流态的瞬态涡量图、瞬态风速图和瞬态风压图((a)升力波峰时刻;(b)升力波谷时刻) Fig. 11 Instantaneous vorticity, velocity field, and pressure field of bias flow when P/D=1.1 |
|
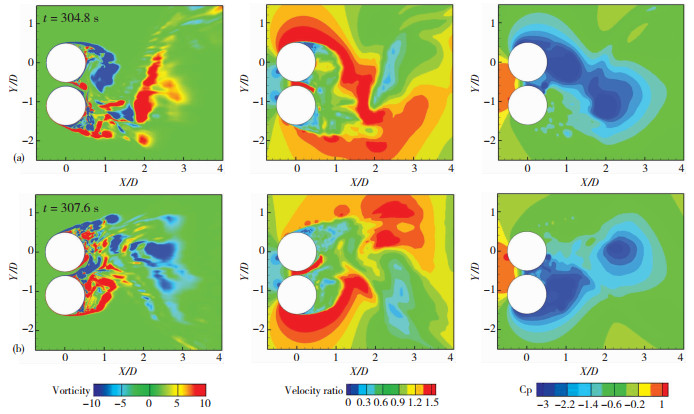
图 12 P/D=1.1单一钝体的瞬态涡量图、瞬态风速图和瞬态风压图((a)升力波峰时刻;(b)升力波谷时刻) Fig. 12 Instantaneous vorticity, velocity field, and pressure field of single-bluff-body flow when P/D=1.1 |
对于偏向流流态(见图 11),两个典型时刻的涡量图、风速图和风压图较相似;由涡量图可见,并列圆柱的尾流均偏向上侧,上侧圆柱的尾流窄而下侧圆柱的尾流宽;从风速场可知,两个圆柱的停滞点明显偏向间隙侧,两个圆柱之间存在高速间隙流;从风压图可见,尾流较窄的上侧圆柱尾流中的负压强度大于下游圆柱,这也导致上侧圆柱的阻力系数大于下游圆柱.
对于单一钝体流态(见图 12),两个时刻的涡量图、风速图和风压图呈现上下对称关系,其流场特性与偏向流流态不同;由涡量图可知,两个圆柱的上下两个表面分离的剪切层会很快卷起形成旋涡,这对旋涡会在近尾流相互作用;由风速图可知,这对旋涡会导致并列圆柱的上下两侧出现大范围的高风速区域,高速间隙流相对较弱;由风压图可知,这对旋涡所在位置有很强的负压,使两个圆柱的气动力产生大幅度的波动.
3 结论采用大涡模拟,在高雷诺数下(Re=1.4×105)对圆心间距P/D=1.1~4并列双圆柱绕流问题进行研究,探究了气动性能和流场流态随间距的变化规律,分析了偏向流流态下的流场特性及其气动性能,进一步澄清了并列双圆柱气动干扰的流场机理,得到以下主要结论:
1) 采用大涡模拟方法得到的并列双圆柱的气动力结果与文献风洞结果吻合良好,模拟得到了单一钝体、偏向流和平行涡街3种不同类型的流态,结果表明大涡模拟方法可以准确模拟高雷诺数下并列双圆柱绕流问题.
2) 当P/D=1.1时,并列圆柱会间歇性地呈现单一钝体和偏向流流态两种流态,圆柱的气动力系数会随时间发生剧烈变化,呈现非稳态特征;单一钝体时并列圆柱的近尾流中有一对强度很大的旋涡,这对旋涡会导致尾流中出现很强的负压区,造成圆柱气动力的大幅度波动.
3) 当P/D=1.2~1.5时,并列圆柱呈现偏向流流态,双圆柱中间的高速间隙流会引起一侧圆柱的尾流变窄,而另一侧圆柱的尾流变宽;偏向流的方向会间歇性发生改变,并且随着间距的增大偏转方向的改变变得更频繁;偏向流流态下,圆柱气动力系数的脉动值很小,并且没有明显的St数.
4) 当P/D=2~4时,随着间距的增大,偏向流现象会逐渐消失,两个圆柱的相互干扰减弱;两个圆柱尾流中均会出现周期性的旋涡脱落,形成两个平行涡街,圆柱气动力的脉动大.
需要指出的是,本文大涡模拟的雷诺数为Re=1.4×105,属于高亚临界雷诺数范围,对于单圆柱来说自由剪切层依属于层流分离.但对于双圆柱来说,圆柱间的相互干扰可能会导致层流向湍流的转捩位置发生改变,也可能会导致层流分离变为湍流分离.这一问题目前尚未有定论,还需进一步研究.
| [1] |
SUMNER D. Two circular cylinders in cross-flow:a review[J]. Journal of Fluids & Structures, 2010, 26(6): 849. |
| [2] |
ALAM M M, ZHOU Y. Flow around two side-by-side closely spaced circular cylinders[J]. Journal of Fluids & Structures, 2007, 23(5): 799. |
| [3] |
ZDARVKOVICH M M. Review of flow interference between two circular cylinders in various arrangements[J]. Journal of Fluids Engineering, 1977, 99(4): 618. DOI:10.1115/1.3448871 |
| [4] |
SUMNER D, RICHARDS M D, AKOSILE O O. Two staggered circular cylinders of equal diameter in cross-flow[J]. Journal of Fluids & Structures, 2005, 20(2): 255. |
| [5] |
ZHOU Y, ZHANG H J, YIU M W. The turbulent wake of two side-by-side circular cylinders[J]. Journal of Fluid Mechanics, 2002, 458(458): 303. |
| [6] |
ZDRAVKOVICH M M. The effects of interference between circular cylinders in cross flow[J]. Journal of Fluids & Structures, 1987, 1(2): 239. |
| [7] |
XU S J, ZHOU Y, SO R M C. Reynolds number effects on the flow structure behind two side-by-side cylinders[J]. Physics of Fluids, 2003, 15(5): 1214. DOI:10.1063/1.1561614 |
| [8] |
ZHOU Y, ALAM M M. Wake of two interacting circular cylinders:a review[J]. International Journal of Heat & Fluid Flow, 2016, 62(2): 510. |
| [9] |
ISHIGAI S, NISHIKAWA E, NISHIMURA E, et al. Experimental study of structure of gas flow in tube banks axes normal to flow[J]. Bulletin of the Japan Society of Mechanical Engineers, 1972, 15(86): 949. DOI:10.1299/jsme1958.15.949 |
| [10] |
MIAU J J, WANG H B, CHOU J H. Flopping phenomenon of flow behind two plates placed side-by-side normal to the flow direction[J]. Fluid Dynamics Research, 1996, 17(6): 311. DOI:10.1016/0169-5983(95)00034-8 |
| [11] |
BEARMAN P W, WADCOCK A J. The interaction between a pair of circular cylinders normal to a stream[J]. Journal of Fluid Mechanics, 1973, 61(3): 499. |
| [12] |
KIM H J, DURBIN P A. Investigation of the flow between a pair of circular cylinders in the flopping regime[J]. Journal of Fluid Mechanics, 1988, 196(196): 431. |
| [13] |
BRUN C, TENCHINE D, HOPFINGER E J. Role of the shear layer instability in the near wake behavior of two side-by-side circular cylinders[J]. Experiments in Fluids, 2004, 36(2): 334. DOI:10.1007/s00348-003-0726-6 |
| [14] |
SUMNER D, WONG S S T, PRICE S J, et al. Fluid behaviour of side-by-side circular cylinders in steady cross-flow[J]. Journal of Fluids & Structures, 1999, 13(3): 309. |
| [15] |
ALAM M M, MORIYA M, SAKAMOTO H. Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon[J]. Journal of Fluids & Structures, 2003, 18(3/4): 325. |
| [16] |
CHANG K S, SONG C J. Interactive vortex shedding from a pair of circular cylinders in a transverse arrangement[J]. International Journal for Numerical Methods in Fluids, 2010, 11(3): 317. |
| [17] |
MENEGHINI J R, SALTARA F, SIQUEIRA C L R, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements[J]. Journal of Fluids & Structures, 2001, 15(2): 327. |
| [18] |
CHEN L, TU J Y, YEOH G H. Numerical simulation of turbulent wake flows behind two side-by-side cylinders[J]. Journal of Fluids & Structures, 2003, 18(3): 387. |
| [19] |
CANTWELL B J, COLES D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder[J]. Fluid Mech, 1983, 136(11): 321. |
| [20] |
NISHIMURA H, TANⅡKE Y. Aerodynamic characteristics of fluctuating forces on a circular cylinder[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 89(7): 713. |
| [21] |
ACHENBACH E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re=5×106[J][J]. Fluid Mech, 1968, 34(4): 625. DOI:10.1017/S0022112068002120 |
| [22] |
KIYA M, SUZUKI Y, ARIE M, et al. A contribution to the free-stream turbulence effect on the flow past a circular cylinder[J]. Journal of Fluid Mechanics, 1982, 115(115): 151. |
| [23] |
SURRY D. Some effects of intense turbulence on the aerodynamics of a circular cylinder at subcritical Reynolds number[J]. Journal of Fluid Mechanics, 1972, 52(3): 543. DOI:10.1017/S0022112072001582 |
| [24] |
NORBERG C. Fluctuating lift on a circular cylinder:review and new measurements[J]. Journal of Fluids & Structures, 2003, 17(1): 57. |
 2019, Vol. 51
2019, Vol. 51


