2. 哈尔滨工程大学 机电工程学院, 哈尔滨 150001
2. School of Mechatronics Engineering, Harbin Engineering University, Harbin 150001, China
随着航天事业高速发展,星载天线正在向敏捷化、复杂化、高精度化方向发展[1~2].固面天线因板面材料多选用金属板或碳纤维增强复合材料,具备很高的形面精度和频带宽,可以极好地适应空间探测、微波遥感及军事领域对天线高精度和宽频带的需求[3-4].另外,可展机构可将固面天线收拢到一定的包络尺寸,克服了运载器对发射空间的限制[5].
目前,固体反射面展开机构技术主要应用在星载天线及射电天文领域.美国TRW公司研制的太阳花式固面展开机构[6],展开后形面精度0.13 mm.欧空局和多尼尔公司联合研制的DAISY可展开天线[7],面板背部采用桁架支撑,形面精度可达8 μm. SSDA固面展开机构[8]结构形式非常特殊,其翼板围绕中心轮毂转动,同步性较高.铰接肋式固体反射面机构[9]由Harris公司设计,支撑肋的特殊设计保证机构具备很好的刚度和形面精度. Spektr-R太空射电望远镜[10-11]搭载“波谱一R”天体物理观测卫星,与地面射电望远镜共同对地面实施观测,拥有很高的角分辨率和工作频域.西北工业大学研制的可展开高精度固面反射面天线[12],独特的拉锁驱动及锁定机构使天线具备很好的刚度和收纳比.上海卫星工程研究所提出一种花瓣式可展开星载抛物面天线[13],两套空间四连杆机构串联连接驱动天线展开,运动同步性较好.
目前, 可展开高精度固体反射面机构的理论与应用研究处于初步阶段,对可展机构的动力学性能分析较少,但其动力学分析可以借鉴索网式、桁架式可展开天线的动力学特性研究. Flores等[14]应用连续碰撞模型,得到了含间隙的平面低副与空间高副的多体动力学特性. MITSUG等[15]建立了含柔性索网的星载抛物面天线机构多柔体动力学模型,并对索网反射面天线的展开过程进行了仿真.国内蒋建平等[16]采用假设模态法和有限元法,对大挠性刚柔耦合卫星天线的动力学进行了研究与校验.
本文设计了一种高收拢率、高形面精度、单一驱动的可展开固面天线机构,并通过机构位置矢量方程,向量封闭投影法,建立了可展机构拉格朗日动力学模型,求解出机构运动过程驱动力并分析运动学参数对驱动力影响.利用Workbench对天线结构动力学性能进行分析,通过Design Exploration优化模块中响应面法分析结构设计参数对可展机构固有频率影响并进行灵敏度分析.研制天线原理样机并进行展开功能和基频测量试验对分析加以验证.
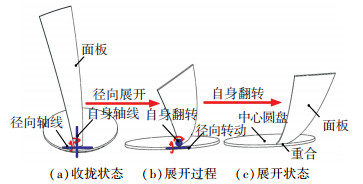
1 天线可展开机构设计 1.1 可展机构构型设计对目前国内外固面天线可展机构展开原理进行分析发现,要实现天线面板由收拢到展开,面板要完成径向向外转动和绕自身轴线翻转的复合运动,面板相对于中心圆盘收拢状态的轴测图、展开过程的正视图、展开状态的轴测图具体如图 1所示.
|
图 1 面板运动状态 Fig. 1 Motion state of panel |
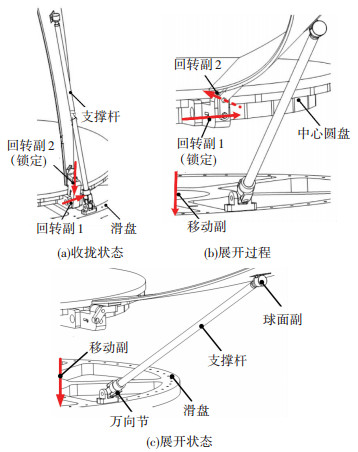
根据面板的运动形式,设计一种高收拢率、高形面精度、单一驱动的可展开固面天线机构.工作原理:面板径向展开时,回转副2锁定,滑盘下移并通过支撑杆拉动使面板绕回转副1作径向展开运动;当面板展开到一定角度,锁定回转副1的同时解锁回转副2,滑盘继续下移带动面板绕回转副2轴线进行翻转,直至机构完全展开并锁定,右手定则判定回转副转向,可展机构运动过程如图 2所示.
|
图 2 可展机构运动过程 Fig. 2 Movement process of deployable mechanism |
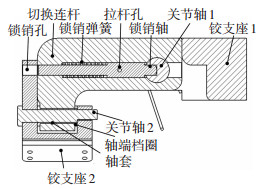
锁定回转副1同时解锁回转副2时锁定解锁切换机构工作原理:面板径向展开时,锁销轴受弹簧预压力左端被压入铰支座2锁销孔内,限制回转副2旋转,右端绕关节轴1作纯滚动;当面板径向展开到位,弹簧力将锁销轴右端压入关节轴1孔内,同时左端立即从铰支座2锁销孔内拔出,此时锁定解锁切换机构全剖视图如图 3所示.总之,国内外现已出现很多种形式的固面天线可展机构.
|
图 3 锁定解锁切换机构剖视图 Fig. 3 Sectional view of locking and releasing mechanism |
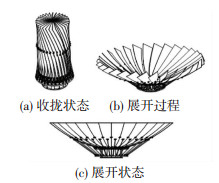
以收拢率作为设计目标,收拢态时面板全部收束到中心圆盘内作为设计原则,优选出面板数量30. 30套可展机构经万向节连接到滑盘,通过电机旋转丝杠,丝母与滑盘固连,带动滑盘下移,并结合锁定解锁切换机构对回转副2先锁定再解锁,进而实现天线所有面板先径向展开再绕自身翻转,直至天线所有面板完全展开,天线展开过程如图 4所示.
|
图 4 所有天线面板展开过程 Fig. 4 Deployment process of all antenna panels |
将可展机构抽象成一单闭环空间连杆机构,各运动副中心建立D-H前置坐标系,运动副中心轴线定为Z轴,相邻连杆间公法线方向定为X轴方向,可展机构运动学模型如图 5所示.

|
图 5 可展机构运动学模型 Fig. 5 Kinematic model of deployable mechanism |
图 5中θi(i=2,3,5,6)为回转副2、3、5和6回转角,d7为滑盘位移输入量,h2为支撑杆长
根据图 5所建D-H坐标系和坐标变换矩阵通式,得到任意坐标系点的坐标在基坐标系下表示为
| $ r_{0}=\boldsymbol{T}_{01} \boldsymbol{T}_{12} \boldsymbol{T}_{23} \cdots \boldsymbol{T}_{(i-1) i} r_{i}=\boldsymbol{A}_{1} \boldsymbol{A}_{2} \boldsymbol{A}_{3} \cdots \boldsymbol{A}_{i} r_{i} $ |
根据机构运动杆长不变条件得机构位置矢量方程为
| $ \begin{array}{l}{\left[\left(a_{3} \mathrm{c} \theta_{3}+a_{2}\right) \mathrm{c} \theta_{2}-\left(d_{3}+d_{4}\right) \mathrm{s} \theta_{2}+a_{1}-a_{5} \mathrm{c} \theta_{7}\right]^{2}-} \\ {\left(a_{3} \mathrm{s} \theta_{3}+a_{5} \mathrm{s} \theta_{7}\right)^{2}+\left[\left(a_{3} \mathrm{c} \theta_{3}+a_{2}\right) \mathrm{s} \theta_{2}\left(d_{3}+d_{4}\right) \mathrm{c} \theta_{2}-\right.} \\ {d_{1}+d_{7} ]^{2}=h^{2}}.\end{array} $ | (1) |
式中:sθi=sin θi,cθi=cos θi,i=(2,3,5,6,7).
可展机构为空间向量封闭形,沿任意轴线投影恒为零,分别向基坐标系X0、Y0和Z0轴投影得方程组:
| $ \begin{array}{c}\left(a_{3} \mathrm{c} \theta_{3}+a_{2}\right) \mathrm{c} \theta_{2}-\left(d_{3}+d_{4}\right) \mathrm{s} \theta_{2}+a_{1}-a_{5} \mathrm{c} \theta_{7}=\\ h\left(\mathrm{c} \theta_{5} \mathrm{c} \theta_{6} \mathrm{c} \theta_{7}-\mathrm{s} \theta_{5} \mathrm{s} \theta_{7}\right) , \end{array} $ | (2) |
| $ h\left(\mathrm{c} \theta_{5} \mathrm{c} \theta_{6} \mathrm{s} \theta_{7}+\mathrm{s} \theta_{5} \mathrm{c} \theta_{7}\right)=-a_{3} \mathrm{s} \theta_{3}-a_{5} \mathrm{s} \theta_{7}, $ | (3) |
| $ \begin{aligned}\left(a_{3} \mathrm{c} \theta_{3}\right.&+a_{2} ) \mathrm{s} \theta_{2}+\left(d_{3}+d_{4}\right) \mathrm{c} \theta_{2}-d_{1}+d_{7}=\\ &-h \mathrm{c} \theta_{5} \mathrm{s} \theta_{6}. \end{aligned} $ | (4) |
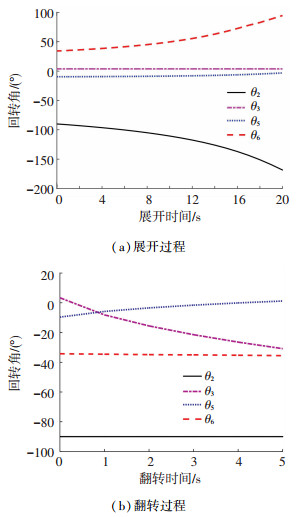
以展开口径2.2 m固面天线为例,滑盘以4 mm/s的速度下移,结合式(1)~(4)求得机构运动过程回转角θ2、θ3、θ5和θ6随时间变化曲线如图 6.
|
图 6 回转角θ随时间变化曲线 Fig. 6 Change curve of rotation angle θ with time |
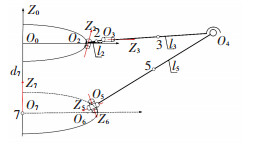
利用D-H坐标变换矩阵推导可展机构拉格朗日动力学方程,所建机构的动力学模型如图 7所示.
|
图 7 可展机构动力学模型 Fig. 7 Dynamic model of deployable mechanism |
其中连杆l2、l3和l5分别代表切换连杆、抛物面板和支撑杆,各连杆及滑盘质心分别为2、3、5和7.
首先,确定可展机构运动过程拉格朗日函数L,连杆i处质心i相对基坐标系下速度矢量为
| $ \boldsymbol{v}_{i}=\frac{\mathrm{d}}{\mathrm{d} t}\left(\boldsymbol{T}_{0 i} \boldsymbol{r}_{i}\right)=\sum\limits_{j=1}^{i} \frac{\partial\left(\boldsymbol{T}_{0 i}\right)}{\partial \theta_{j}} \frac{\mathrm{d} \theta_{j}}{\mathrm{d} t} \cdot \boldsymbol{r}_{i}=\sum\limits_{j=1}^{i} \boldsymbol{U}_{i j} \frac{\mathrm{d} \theta_{j}}{\mathrm{d} t} \cdot \boldsymbol{r}_{i}, $ |
则连杆i质量单元的动能为
| $ \mathrm{d} K_{i}=\frac{1}{2} \operatorname{tr}\left[\left(\sum\limits_{p=1}^{i} \boldsymbol{U}_{i p} \frac{\mathrm{d} \theta_{p}}{\mathrm{d} t} \cdot \boldsymbol{r}_{i}\right)\left(\sum\limits_{r=1}^{i} \boldsymbol{U}_{i r} \frac{\mathrm{d} \theta_{r}}{\mathrm{d} t} \cdot \boldsymbol{r}_{i}\right)\right] \mathrm{d} m. $ |
式中:p和r为不同节点坐标系编号,tr为矩阵的迹,表示矩阵主对角线上元素之和.则机构最终动能形式为
| $ K=\frac{1}{2} \sum\limits_{i=1}^{n} \sum\limits_{p=1}^{i} \sum\limits_{r=1}^{i} \operatorname{tr}\left(\boldsymbol{U}_{i p} \boldsymbol{J}_{i} \boldsymbol{U}_{i r}^{\mathrm{T}}\right) \theta_{p}^{i} \theta_{r}^{i}. $ |
式中:Ji为连杆i质心相对于连杆坐标系Oi惯量矩阵.
将各连杆质心i相对于基坐标系下势能相加
| $ P=\sum\limits_{i=1}^{n} P_{i}=\sum\limits_{i=1}^{n}\left[-m_{i} \boldsymbol{g}^{\mathrm{T}} \cdot\left(\boldsymbol{T}_{0 i} \boldsymbol{r}_{i}\right)\right]. $ |
式中:gT为重力矩阵(1×4矩阵);n为连杆数.
机构最终的拉格朗日函数L可表示为
| $ \begin{aligned} L=& \frac{1}{2} \sum\limits_{i=1}^{n} \sum\limits_{p=1}^{i} \sum\limits_{r=1}^{i} \operatorname{tr}\left(\boldsymbol{U}_{i p} \boldsymbol{J}_{i} \boldsymbol{U}_{i r}^{\mathrm{T}}\right) \theta_{p}^{i} \theta_{r}^{i}-\\ & \sum\limits_{i=1}^{n}\left[-m_{i} \boldsymbol{g}^{\mathrm{T}} \cdot\left(\boldsymbol{T}_{0 i} \boldsymbol{r}_{i}\right)\right]. \end{aligned} $ |
可展机构径向展开过程需计算连杆2、3、5和滑盘7的动能;而机构翻转过程需计算连杆3、5和滑盘7的动能.以可展机构径向展开过程为例,求得可展机构径向展开过程拉格朗日函数为
| $ L=\sum K_{i}+\sum P_{i}(i=2, 3, 5, 7). $ |
滑盘以4 mm/s速度匀速下移,机构展开时间为20 s,以d7作为广义坐标变量,根据式(5)求得机构运动过程驱动力随时间变化曲线如图 8所示.

|
图 8 机构运动过程中驱动力变化曲线 Fig. 8 Change curve of driving force in the motion process |
| $ F=\frac{\partial}{\partial t}\left(\frac{\partial L}{\partial \dot{d}_{7}}\right)-\frac{\partial L}{\partial d_{7}}. $ | (5) |
式中F为机构中滑盘作直线运动时所需驱动力.
由图 8可知,可展机构展开过程驱动力比翻转过程小很多,机构在翻转运动一开始所需驱动力较大,之后随翻转时间的增加所需驱动力迅速减小.
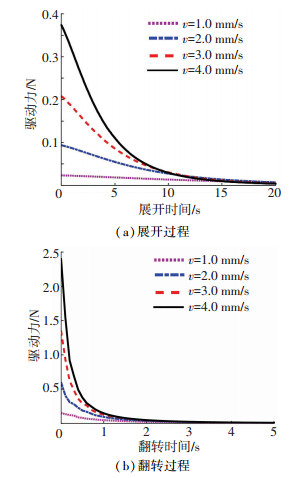
2.4 驱动力影响因素分析 2.4.1 输入速度滑盘以v=1.0、2.0、3.0和4.0 mm/s速度匀速下移,得到可展机构运动过程驱动力随时间变化曲线如图 9所示(这里仅取机构展开运动前20 s和翻转运动前5 s),分析发现减小输入速度,可以有效地减小机构运动过程所需驱动力.
|
图 9 输入速度与驱动力关系 Fig. 9 Relationship between input speed and driving force |
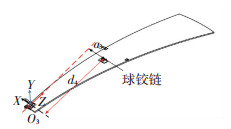
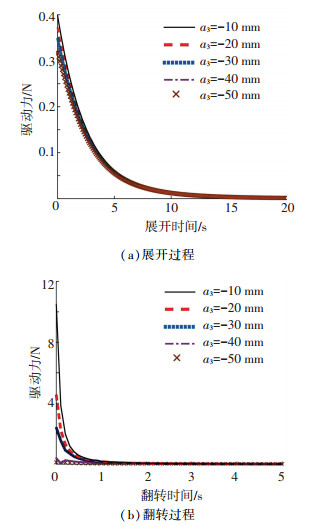
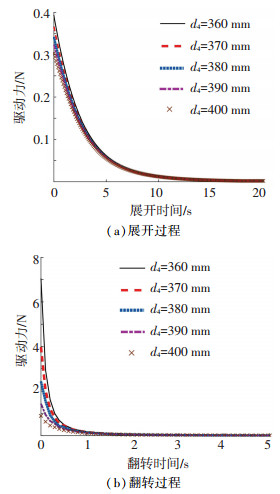
选取坐标系O3作为参考坐标系,参数a3和d4决定球铰链安装位置,如图 10所示.通过改变位置参数a3和d4,求解出球铰链安装位置参数a3和d4对机构运动过程驱动力的影响,如图 11和图 12所示.
|
图 10 所选参考坐标系O3及安装位置参数 Fig. 10 Selected reference coordinate system O3 and installation position parameters |
|
图 11 参数a3对所需驱动力影响 Fig. 11 Effect of parameter a3 on driving force |
|
图 12 参数d4对所需驱动力影响 Fig. 12 Effect of parameter d4 on driving force |
由图 11和图 12可知,球铰链安装位置参数a3和d4对可展机构径向展开过程驱动力影响较小,但对其自身翻转过程驱动力影响较大,并且a3比d4对机构翻转过程驱动力的影响要大得多.考虑到位置参数a3越偏离参考坐标系O3的X轴负向,天线相邻面板间球铰链安装空间越小,选定球铰链安装位置为a3=-30 mm,d4=380 mm.
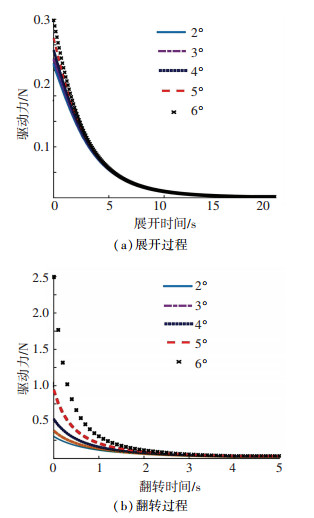
2.4.3 滑盘与中心圆盘初始夹角θ7以球铰链安装位置a3=-30 mm,d4=380 mm, 输入速度v=4.0 mm/s作为分析基础,分析回转角θ7对可展机构运动过程所需驱动力的影响,得到θ7为2°、3°、4°、5°、6°时机构运动过程中所需驱动力随时间变化曲线如图 13所示.
|
图 13 回转角θ7对所需驱动力影响 Fig. 13 Effect of rotation angle θ7 on driving force |
由图 13可知,回转角θ7越大,机构展开和翻转运动过程驱动力越大,回转角θ7对机构翻转过程驱动力的影响比展开过程大很多,为避免同一可展机构各零件间发生运动干涉,确定初始夹角θ7=5°.
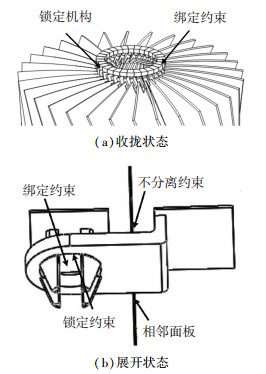
3 天线结构动力学性能分析 3.1 天线固有频率分析将Croe软件中建立的简化模型导入Workbench软件中,分析天线收拢和展开状态下固有频率.定义各零件材料及约束,其中零件之间固定采用绑定约束,转动和滑动采用不分离约束,收拢状态下天线各面板顶端锁定机构间定义绑定约束,展开状态下天线相邻面板侧面间定义不分离约束,面板间锁定机构定义绑定约束,收拢和展开状态天线面板间所添加约束如图 14所示.
|
图 14 天线面板间所添加约束 Fig. 14 Constraints added between antenna panels |
天线收拢、展开状态下前六阶固有频率如表 1.
| 表 1 天线收拢、展开状态下以及可展机构展开状态下的前六阶固有频率 Tab. 1 Antenna first six order natural frequencies in the closed and deployed states and first six order natural frequencies of the developable machanism in the deployed state |
收拢状态下一阶阵型对应天线整体结构弯曲, 二阶对应整体结构扭转, 三、四阶对应四周面板弯曲且对称分布,五、六阶对应四周局部面板发生弯曲,收拢状态下天线整体结构固有频率>20 Hz,满足设计要求.
天线展开状态下一、二、四阶阵型对应天线整体结构发生弯曲扭转,三阶对应天线整体结构绕支座中心扭转,五、六阶对应天线整体结构发生弯曲.展开状态下天线固有频率>3 Hz,满足设计要求.
3.2 可展机构固有频率分析对展开状态下天线可展机构进行模态分析,得到可展机构前六阶固有频率如表 1所示,其中一、三、五阶阵型主要变现为面板的弯曲扭转,二、四、六阶阵型主要表现为面板的弯曲.
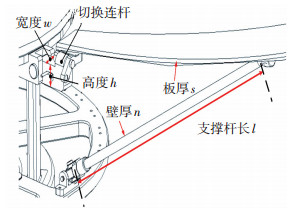
考虑到收拢状态天线各面板零件不能出现干涉,确定面板厚度s=6 mm,分析相关零件尺寸参数对可展机构固有频率的影响.需分析的零件尺寸参数包括:支撑杆长度l、壁厚n,切换连杆高度h、宽度w,具体零件尺寸参数如图 15所示.
|
图 15 选取的相关零件尺寸参数 Fig. 15 Parameters of selected component size |
利用Croe建模软件与Workbench分析软件数据共享接口,将可展机构中相关零件尺寸及前三阶固有频率参数化,利用Design Exploration优化模块中响应面法分析结构参数对可展机构固有频率影响.
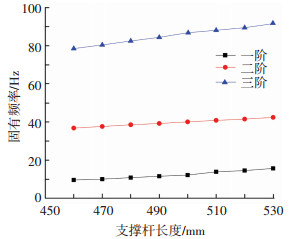
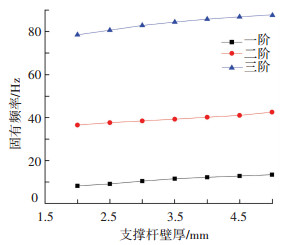
3.2.1 支撑杆长度l和壁厚n影响取支撑杆长度依次为460、470、480、490、500、510、520、530 mm,支撑杆壁厚分别为2.0、2.5、3.0、3.5、4.0、4.5、5.0 mm,得到可展机构前三阶固有频率变化曲线分别如图 16和17所示.
|
图 16 固有频率随支撑杆长度变化曲线 Fig. 16 Change curves of natural frequency with size l |
|
图 17 固有频率随壁厚变化曲线 Fig. 17 Change curves of natural frequency with size n |
由图 16和17可知,支撑杆长度增加,可展机构前三阶固有频率明显增加;支撑杆壁厚增加,可展机构前三阶固有频率出现较明显增加,支撑杆长度及壁厚增加对可展机构前三阶固有频率影响较大.
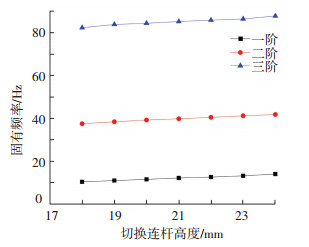
3.2.2 切换连杆高度h及宽度w影响.分别取切换连杆高度为18、19、20、21、22、23、24 mm,切换连杆宽度为13、14、15、16、17、18、19、20 mm,得到可展机构前三阶固有频率变化曲线分别如图 18和19所示.
|
图 18 固有频率随切换连杆高度变化曲线 Fig. 18 Change curves of natural frequency with size h |
|
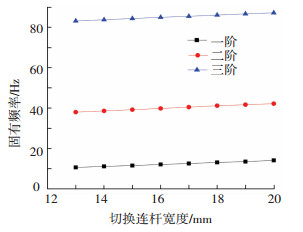
图 19 固有频率随切换连杆宽度变化曲线 Fig. 19 Change curves of natural frequency with size w |
由图 18、19可知,切换连杆高度增加,可展机构前三阶固有频率略微增加;宽度增加,可展机构前三阶固有频率也增加,但变化并不明显,这说明切换连杆宽度和高度对机构前三阶固有频率影响较小.
利用Workbench分析软件,通过实验设计DOE法,以中心组合设计的方法对上述结构参数进行设计点采样,分析上述结构参数对可展机构前三阶固有频率的影响灵敏度,所得分析结果如图 20所示.
|
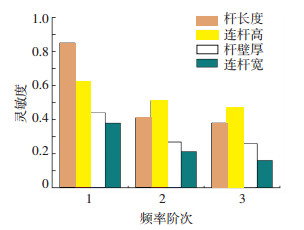
图 20 结构参数对固有频率影响 Fig. 20 Influence of sensitivity of structural parameters on natural frequency |
由图 20可知,支撑杆长度对可展机构前三阶固有频率影响最大;壁厚对可展机构前三阶固有频率影响较大;切换连杆高度和宽度对可展机构前三阶固有频率影响较小;切换连杆高度和宽度对可展机构基频影响较大,可通过增加切换连杆高度和宽度,适当提高机构基频.
4 天线展开功能试验和模态测试详细设计并优选了可展开固面天线结构,采用3D打印技术,从实用性和经济性角度出发,仅加工制作球铰链到中心圆盘位置的面板,同时参照可展单元运动分析中各杆件尺寸,制作了展开状态2.2 m固面天线等比缩小50%的模型.在有重力的情况下,手动滑盘下移,发现固面天线可以平稳展开到位,天线展开过程如图 21所示,从原理上验证了固面天线可展机构重复展开功能.

|
图 21 固面天线展开过程 Fig. 21 Deployment process of solid surface antenna |
模态测试采用LMS SCADAS Ⅲ多通道振动测试分析仪,加速度传感器为BK的三轴ICP加速度传感器,天线底座固定在光学水平台上,采用锤击法对可展开固面天线进行模态测试.
利用LMS Test Lab软件中Poly MAX模块合成各测量结果,去除噪声扰动等干扰,选取天线前三阶模态,得到展开状态下天线模态测量结果如表 2所示.将展开状态1.1 m固面天线各阶频率和阵型的测试结果与仿真结果作对比,发现二者阵型吻合,试验测得的各阶频率要低于仿真结果,这是由于天线样机各铰链由于加工装配误差等原因存在间隙,削弱了系统的刚度.
| 表 2 展开状态天线前三阶频率测试结果与仿真结果 Tab. 2 Test and simulation results of first three order frequencies of solid surface antenna in deployed state |
1) 设计了一种高收拢率、高精度、单一驱动的可展开固面天线机构,研制了天线原理样机并通过试验验证了可展机构可重复实现天线展开功能.
2) 建立了可展机构拉格朗日动力学模型,求解出机构运动过程驱动力,分析出机构翻转比展开过程驱动力大很多,可通过减小输入速度、调整球铰位置和减小初始夹角θ7来降低机构翻转过程驱动力.
3) 收拢和展开状态下天线基频满足设计要求,支撑杆尺寸设计参数对可展机构基频的影响比切换连杆要大很多,可通过增加切换连杆高度h和宽度w适当提高机构基频.对展开状态1.1 m固面天线样机进行模态测试和仿真分析,发现测试和仿真结果阵型吻合,试验测得天线前三阶频率要低于仿真结果,可展开固面天线具备很好的动力学性能.
| [1] |
LIU Ruiwei, GUO Hongwei, LIU Rongqiang, et al. Shape accuracy optimization for cable-rib tension deployable antenna structure with tensioned cables[J]. Acta Astronautica, 2017, 140: 66. DOI:10.1016/j.actaastro.2017.07.047 |
| [2] |
LIU Ruiwei, GUO Hongwei, LIU Rongqiang, et al. Structural design and optimization of large cable-rib tension deployable antenna structure with dynamic constraint[J]. Acta Astronautica, 2018, 151: 160. DOI:10.1016/j.actaastro.2018.05.055 |
| [3] |
MIYASAKA A, HOMMAT M, TSUJIGATA A. Design and ground verification of large deployable reflector[C]//42th AIAA/ASME/ASCE/AHS/ASC/ Structures, Structural Dynamics, and Materials Conference and Exhibit. Seattle: WA, 2001: 2222
|
| [4] |
MEGURO A, HARADA S, WATANABE M. Key technologies for high-accuracy large mesh antenna reflectors[J]. Acta Astronautica, 2003, 53(11): 899. DOI:10.1016/S0094-5765(02)00211-4 |
| [5] |
罗阿妮, 刘贺平, 李杨, 等. 花瓣式可展天线的结构分析[J]. 中国机械工程, 2012, 23(14): 1656. LUO Ani, LIU Heping, LI Yang, et al. Structure analysis of petal deployable antenna[J]. Journal of Mechanical Engineering of China, 2012, 23(14): 1656. DOI:10.3969/j.issn.1004—132X.2012.14.004 |
| [6] |
PALMER W B, GIEBLER M M. Large solid deployable reflector[R]. Pasadena: TRW Defense and Space Systems Group, Redondo Beach, 1979: 380
|
| [7] |
TAN L T, PELLEGRINO S. Stiffness design of spring back reflectors[C]//43th AIAA /ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Denver: AIAA, 2002: 2307
|
| [8] |
TIBERT G. Deployable tensegrity structures for space applications[D]. Stockholm: Royal Institute of Technology Department of Mechanics, 2002
|
| [9] |
HOLLAND H. Collapsible antenna with plurality of exible rector petals releasably retained: US17477662A[P]. 1965-03-30
|
| [10] |
KARDASHEV N S, KHARTOV V V, ABRAMOV V V, et al. "Radio Astron"-A telescope with a size of 300000 km: Main parameters and first observational results[J]. Astronony Rerorts, 2013, 57(3): 153. DOI:10.1134/S1063772913030025 |
| [11] |
FEDORCHUK S D, ARKHIPOV M Y. On the assurance of the design accuracy of the space radio telescope radioastron[J]. Kosmicheskie Issledovaniya, 2014, 52(5): 415. DOI:10.1134/S0010952514050049 |
| [12] |
HUANG He, GUAN Fuling, XU Yan, et al. Design and deploying study of a new petal-type deployable solid surface Antenna[J]. Acta Astronautica, 2018(148): 99. |
| [13] |
张如变, 王智磊, 赵枝凯, 等.花瓣式可展开星载抛物面天线: CN107768796A[P].2018-03-06 ZHANG Rubian, WANG Zhilei, ZHAO Zhikai, et al. Petal-shaped deployable space-borne parabolic antenna: CN107768796A[P].2018-03-06 |
| [14] |
FLORES P, LEINE R, GLOCKER C. Modeling and analysis of rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach[J]. Multibody System Dynamics, 2010, 23(2): 165. DOI:10.1007/s10409-014-0021-1 |
| [15] |
MITSUGI J, ANDO K, SENBOKUYA Y, et al. Deployment analysis of large space antenna using flexible multibody dynamics simulation[J]. Acta Astronautica, 2000, 47(1): 19. DOI:10.1016/S0094-5765(00)00014-X |
| [16] |
蒋建平.大挠性多体结构卫星刚柔耦合动力学研究[D]长沙: 国防科学技术大学, 2004 JIANG Jianping. Researches on rigid-flexible coupling dynamics of the flexible multibody satellite[D] Changsha: National University of Defense Technology, 2004 http://cdmd.cnki.com.cn/Article/CDMD-90002-2005143601.htm |
 2019, Vol. 51
2019, Vol. 51


