机械臂对接半物理(HIL)仿真是地面研究对接硬件、对接初始条件和对接策略的主要手段,是成功实现空间对接的前提[1-2].机械臂对接HIL仿真系统中的机械臂通常建立为数学模型,以方便研究不同机械臂的对接特性.但对接过程中高的物理接触刚度容易导致HIL仿真系统发散[3-7].本文提出了将机械臂由六维物理弹簧等效的方法并设计了机械臂对接HIL仿真系统.通过设计六维弹簧机构可以将机械臂的等效刚度引入到半物理仿真系统中,通过较低的机械臂刚度减小对接系统的物理接触刚度,提高系统的稳定性.
机械臂对接HIL仿真系统中运动模拟器的延迟会严重影响HIL仿真系统的稳定性和复现精度.目前,已有文献针对空间对接地面仿真系统进行了研究. Yang等[8-9]应用串联机构分别模拟两个刚性浮动航天器的对接过程,通过重力补偿方式模拟微重力环境;但文献中并没有系统特性的分析. Qi等[10]针对运动模拟器的延迟导致系统不稳定的问题,提出了一种基于泰勒级数低阶模型补偿方法,应用二阶超前补偿器对模拟器进行补偿,提高了系统的稳定性. Qi等[11]针对运动模拟器延迟问题,提出了阻尼和弹性接触力补偿方法;应用相位超前力补偿器使补偿力接近于动力学模型计算的航天器位置对应的理想力,降低了系统的滞后影响.上述文献对延迟补偿方法进行了研究,但没有系统地研究延迟影响下参数对系统稳定性的影响及稳定边界条件等问题. Zebenay等[6, 12]将HIL仿真系统中的串联机器人建立为二阶时滞系统,并以卫星质量、接触刚度和阻尼为参数,导出了临界时滞系数和频率的函数表达式,应用极点配置法得到了满足系统稳定时各指标的取值关系. Chang[13]、Yan[14]和张文辉等[2]建立了基于两个刚性航天器碰撞的HIL仿真系统模型,得到了动力学频率基频与机器人频宽的制约关系.但文献中的研究对象均为两个刚性物体,且大多用串联机器人模拟航天器的运动.本文的研究对象为机械臂空间对接,HIL仿真系统中加入了机械臂(六维弹簧机构)和末端执行器,使得接触环境变为多刚度、多阻尼和单质量接触,接触环境和系统模型均变得复杂;系统参数及其对系统特性的影响也变得多样化.同时,本研究用并联机器人模拟航天器的运动.在新的研究背景下,为保证所提出的机械臂对接HIL仿真系统能够准确有效模拟对接过程,需要全面地对HIL系统的特性进行研究.主要思路如下:
1) 分别建立机械臂为数学模型和六维弹簧机构实物的HIL仿真系统模型,分析系统接触刚度等参数对稳定性的影响,说明本文提出的HIL仿真系统对于解决高刚度接触导致系统发散的有效性.
2) 从HIL仿真系统参数配置关系、稳定条件和动力学频率模拟能力3个评定系统特性的重要方面综合研究机械臂等效为六维弹簧机构的HIL仿真系统的稳定性和复现精度.
3) 通过实验验证思路1);通过仿真和实验验证思路2).
1 机械臂对接半物理仿真系统介绍空间对接系统由航天器、末端执行器、目标适配器、机械臂和空间站组成(对接时空间站保持静止),如图 1所示.由于机械臂在对接过程中各关节处于锁紧状态以消除机械臂端部大范围运动对对接产生的不利影响[15],则机械臂的运动状态体现为弹性变形,将机械臂视为由可变形的柔性部分和不可变形的刚性部分组成.机械臂的柔性部分等效到末端执行器的尾部,则机械臂的刚性部分和空间站可视为静止不动的整体.对接过程中,末端执行器在尾部柔性环节和接触力的作用下运动.
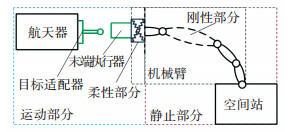
|
图 1 机械臂对接系统 Fig. 1 Manipulator docking system |
模拟机械臂对接的半物理仿真系统如图 2所示.物理实物由末端执行器、六维弹簧机构(机械臂柔性环节)、目标适配器、六自由度并联机器人、力传感器和机械框架组成.力传感器安装在机械框架的下面,六维弹簧机构放置在力传感器和末端执行器之间.力传感器采集接触力数据,当机械臂为弹簧机构物理实物时,动力学模型通过接触力计算航天器的运动,并由并联机器人复现运动过程.当机械臂为数学模型时,则图 2中无六维弹簧机构,动力学模型计算航天器和机械臂端部的相对运动,并由并联机构复现相对运动过程.在本研究中,动力学计算和六自由度并联机器人控制分别由两套上下位机完成.
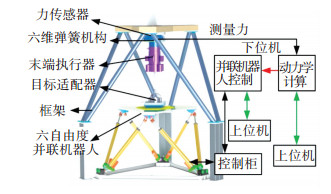
|
图 2 机械臂对接半物理仿真系统 Fig. 2 Manipulator docking HIL simulation system |
机械臂对接半物理仿真系统模型可描述为如图 3形式.

|
图 3 机械臂对接半物理仿真系统模型 Fig. 3 Model of the manipulator docking HIL system |
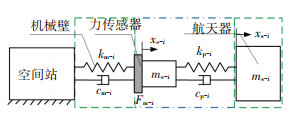
图 1中机械臂的柔性环节、对接机构和航天器是串联形式.柔性环节和接触环节均视为六维弹簧阻尼系统,且仅考虑6个自由度的主刚度.由于6个方向的主刚度解耦,则6个方向的对接动力学形式相同,由于6个自由度模拟参数范围相似,则可以通过单个方向的对接特性说明六自由度系统的对接特性.单个自由度的对接示意图如图 4所示,图中各机构处于同一水平线不表示机构的实际对接位置,仅表示单个自由度的对接动力学原理,虚线框为数学模型,点划线框为物理实物.图中物理量描述第i(i=1~6)自由度的平动/转动参数:xe-i和xs-i分别为末端执行器和航天器位移/转角的大小(正方向为xe轴正向/逆时针方向);kp-i和cp-i分别为平动接触刚度/转动接触刚度和平动接触阻尼/转动接触阻尼;km-i和cm-i分别为机械臂的平动刚度/转动刚度和平动阻尼/转动阻尼;me-i和ms-i分别为末端执行器和航天器的质量/惯量.
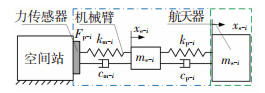
|
图 4 机械臂为六维弹簧机构的单自由度对接原理 Fig. 4 Single degree-of-freedom docking principle with manipulator as a six-dimensional spring mechanism |
为方便描述和建模,以竖直方向单自由度平动为例建立半物理仿真系统模型并去掉物理量自由度标识i.推导接触力Fp与xs的关系和接触模型传递函数为
| $ F_{\mathrm{p}}=\frac{\left(k_{\mathrm{m}}+c_{\mathrm{m}} s\right)\left(k_{\mathrm{p}}+c_{\mathrm{p}} s\right)}{m_{\mathrm{e}} s^{2}+\left(c_{\mathrm{m}}+c_{\mathrm{p}}\right) s+k_{\mathrm{m}}+k_{\mathrm{p}}} x_{\mathrm{s}}. $ |
机械臂为六维弹簧机构的系统对接动力学模型为
| $ x_{\mathrm{s}}^{\prime}=-\frac{F_{\mathrm{p}}}{m_{\mathrm{s}} s^{2}}. $ |
针对每一个自由度,伺服电机控制的并联机器人位置闭环控制传递函数可表示为
| $ G(s)=\frac{K_{V}}{\frac{s^{3}}{\omega_{\mathrm{n}}^{3}}+\frac{2 \xi}{\omega_{\mathrm{n}}} s^{2}+s+K_{V}}, $ |
函数中的参数可以由试验辨识确定.
2.4 机械臂对接半物理仿真系统模型由接触模型、动力学模型和并联机器人模型可建立图 3所示的机械臂对接半物理仿真系统模型.机械臂为六维弹簧机构的半物理仿真系统模型如图 5所示.
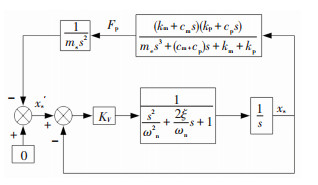
|
图 5 机械臂为六维弹簧机构的半物理仿真系统模型 Fig. 5 HIL simulation system model with manipulator as a six-dimensional spring mechanism |
机械臂为数学模型的对接动力学原理如图 6所示,虚线框为数学模型,点划线框为物理实物.可得到机械臂为数学模型的半物理仿真系统模型如图 7所示.
|
图 6 机械臂为数学模型的单自由度对接原理 Fig. 6 Single degree-of-freedom docking principle with manipulator as a mathematical model |

|
图 7 机械臂为数学模型的半物理仿真系统模型 Fig. 7 HIL simulation system model with manipulator as a mathematical model |
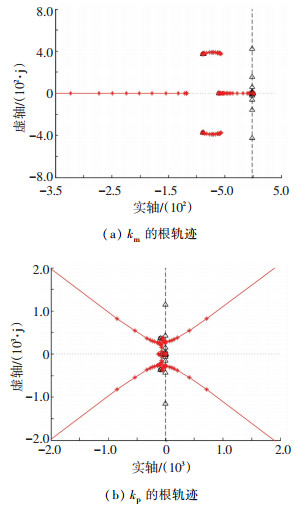
应用根轨迹法分别分析机械臂为六维弹簧机构的半物理仿真系统(后文简称为系统Ⅰ)和机械臂为数学模型的半物理仿真系统(后文简称为系统Ⅱ)中刚度参数对系统特性的影响.根轨迹分析参数:km=10 kN/m, kp=10 kN/m, cm=0.8 kN/(m·s-1), cp=0.8 kN/(m·s-1), ms=5 000 kg, me=500 kg, KV=10 Hz, ωn=65 Hz, ξ=0.3,分析结果如图 8所示.
|
----△为系统Ⅰ中参数的根轨迹分析曲线,---*为系统Ⅱ中参数的根轨迹分析曲线. 图 8 根轨迹分析结果 Fig. 8 Results of root locus analysis |
图 8(a)为km的根轨迹曲线,km在0~+∞范围内均能保证系统稳定,说明当接触刚度较小时,机械臂刚度对系统稳定性影响小.
图 8(b)为kp的根轨迹曲线.当kp过大时,系统Ⅱ变得不稳定;kp在0~+∞范围内,系统Ⅰ均稳定.说明机械臂刚度较小时,系统Ⅰ能够模拟更高的接触刚度,机械臂为物理模型改善了高接触刚度对系统稳定性的影响.
3.2 机械臂为六维弹簧机构的半物理仿真系统参数配置和稳定条件分析图 5的半物理仿真系统的开环传递函数如式(1)所示.
| $ \begin{aligned} G_{\mathrm{k}}(s)=& \frac{k_{\mathrm{p}} k_{\mathrm{m}}}{\left(k_{\mathrm{p}}+k_{\mathrm{m}}\right) m_{\mathrm{s}}} \cdot\left(\frac{s}{k_{\mathrm{m}} / c_{\mathrm{m}}}+1\right) \cdot\left(\frac{s}{k_{\mathrm{p}} / c_{\mathrm{p}}}+1\right) / \\ &\left[{s_{\mathrm{p}}^{2}\left(\frac{s}{K_{V}}+1\right) \cdot\left(\frac{s^{2}}{\left(k_{\mathrm{p}}+k_{\mathrm{m}}\right) / m_{\mathrm{e}}}+\frac{\left(c_{\mathrm{p}}+c_{\mathrm{m}}\right)}{\left(k_{\mathrm{p}}+k_{\mathrm{m}}\right)} s+1\right)}\right.\cdot\\ &\left. {\left(\frac{s^{2}}{\omega_{\mathrm{n}}^{2}}+\frac{2 \xi-K_{V} / \omega_{\mathrm{n}}}{\omega_{\mathrm{n}}} s+1\right) } \right]. \end{aligned} $ | (1) |
若系统的开环传递函数的穿越频率在中、低频段,且系统穿越频率处在大约-20 dB/dec段,则可使系统获得较大的相位裕量和稳定裕量.以此为原则分析系统具有较好特性时系统参数的配置关系.
本研究中半物理仿真系统的参数有如下特点:KV约为10 Hz;ωn约为65 Hz;km和kp一般不大于106 N/m量级,me和ms均大于100 kg;由km、kp和me组成的二阶震荡环节的转折频率ω≤10 Hz;设开环传递函数中各环节的转折频率分别为1/T1=ω,1/T2=kp/cp,1/T3=KV,1/T4=km/cm,1/T5=ωn.则根据参数关系有:1/T3 < 1/T5.满足系统穿越频率处在-20 dB/dec段的伯德图如图 9(a)和图 9(b)所示.

|
图 9 系统参数满足式(2)和(3)的系统示意伯德图 Fig. 9 System schematic Bode diagram when system parameters satisfy formulas (2)and (3) |
图 9(a)中参数配置关系为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{T_4}}}\left( {\frac{1}{{{T_2}}}} \right) < \frac{1}{{{T_2}}}\left( {\frac{1}{{{T_4}}}} \right) < \frac{1}{{{T_3}}} < \frac{1}{{{T_1}}} < \frac{1}{{{T_5}}};}\\ {\log \left( {\left| {G\left( {\frac{1}{{{T_3}}}} \right)} \right|} \right) > 0.且\log \left( {\left| {G\left( {\frac{1}{{{T_1}}}} \right)} \right|} \right) < 0.} \end{array}} \right. $ | (2) |
若满足图 9(b)的穿越情况,则系统开环传递的其他环节的转折频率大小可任意排列.设大于1/T2或1/T4的下一个转折频率为1/Tx,则满足系统穿越频率处在大约-20 dB/dec段的参数配置关系为
| $ \left\{ \begin{array}{l} \frac{1}{{{T_4}}}\left( {\frac{1}{{{T_2}}}} \right) < 其他转折频率, \\ \log \left( {\left| {G\left( {\frac{1}{{{T_2}}}} \right)} \right|} \right) > 0且\log \left( {\left| {G\left( {\frac{1}{{{T_x}}}} \right)} \right|} \right) < 0, \\ 或\log \left( {\left| {G\left( {\frac{1}{{{T_4}}}} \right)} \right|} \right) > 0且\log \left( {\left| {G\left( {\frac{1}{{{T_x}}}} \right)} \right|} \right) < 0. \end{array} \right. $ | (3) |
对接系统的参数有时不满足式(2)和(3)的关系,为保证实验的稳定性,需要求得系统的稳定条件.根据半物理仿真系统的开环传递函数频域特性可知,(kpkm/(kp+km))/ms不宜过大,以保证系统的穿越频率在中、低频段内(高频段系统一定不稳定).鉴于该前提有并联机器人的固有频率ωn远大于系统穿越频率ωc,则并联机器人的二阶震荡环节的频域特性对转折频率处的频域特性影响很小,可忽略其影响.应用劳斯判据可得到半物理仿真系统的稳定条件如式(4)所示.
| $ \left\{ \begin{array}{l} {K_V} > \max \left[ {\frac{{{c_{\rm{m}}}{c_{\rm{p}}}}}{{{m_{\rm{s}}}\left( {{c_{\rm{m}}} + {c_{\rm{p}}}} \right)}}\quad \frac{{{k_{\rm{m}}}{k_{\rm{p}}}}}{{{c_{\rm{m}}}{k_{\rm{p}}} + {c_{\rm{p}}}{k_{\rm{m}}}}}} \right], \\ {m_{\rm{e}}} < \frac{{\left[ {{m_{\rm{s}}}{K_V}\left( {{c_{\rm{m}}} + {c_{\rm{p}}}} \right) - {c_{\rm{m}}}{c_{\rm{p}}}} \right]\left[ {{m_{\rm{s}}}\left( {{k_{\rm{m}}} + {k_{\rm{p}}}} \right) + {c_{\rm{m}}}{c_{\rm{p}}}} \right]}}{{{m_{\rm{s}}}\left[ {{K_V}\left( {{c_{\rm{p}}}{k_{\rm{m}}} + {c_{\rm{m}}}{k_{\rm{p}}}} \right) - {k_{\rm{m}}}{k_{\rm{p}}}} \right]}}, \\ {m_{\rm{s}}}\left( {{k_{\rm{m}}} + {k_{\rm{p}}}} \right) + {c_{\rm{m}}}{c_{\rm{p}}} > \frac{{{m_{\rm{s}}}{m_{\rm{e}}}\left[ {{K_V}\left( {{c_{\rm{p}}}{k_{\rm{m}}} + {c_{\rm{m}}}{k_{\rm{p}}}} \right) - {k_{\rm{m}}}{k_{\rm{p}}}} \right]}}{{{m_{\rm{s}}}{K_V}\left( {{c_{\rm{m}}} + {c_{\rm{p}}}} \right) - {c_{\rm{m}}}{c_{\rm{p}}}}}\\ + \frac{{{k_{\rm{m}}}{k_{\rm{p}}}\left[ {{m_{\rm{s}}}{K_V}\left( {{c_{\rm{m}}} + {c_{\rm{p}}}} \right) - {c_{\rm{m}}}{c_{\rm{p}}}} \right]}}{{{K_V}\left( {{c_{\rm{p}}}{k_{\rm{m}}} + {c_{\rm{m}}}{k_{\rm{p}}}} \right) - {k_{\rm{m}}}{k_{\rm{p}}}}}. \end{array} \right. $ | (4) |
系统中的质量过小或系统刚度过大均会导致系统不稳定.间接体现了对接动力学频率会对系统稳定性产生影响.
3.3 基于3D根轨迹法的半物理仿真系统动力学频率模拟能力分析式(2)、(3)和(4)的数学关系复杂且抽象.机械臂对接动力学过程是一个两自由度有阻尼震荡过程.有两个固有频率(后文称为对接动力学频率)ωlow、ωhigh和两个对接动力学阻尼比ξ1、ξ2[16].本文以半物理仿真系统的稳定性和复现精度为目标,研究对接动力学频率和对接动力学阻尼比对系统特性的影响.分析不同对接动力学阻尼比条件下系统能够模拟的对接动力学频率范围,得到保证系统稳定性和复现精度的对接动力学频率与并联机器人频宽的数值关系(衡量动力学模拟能力的指标).
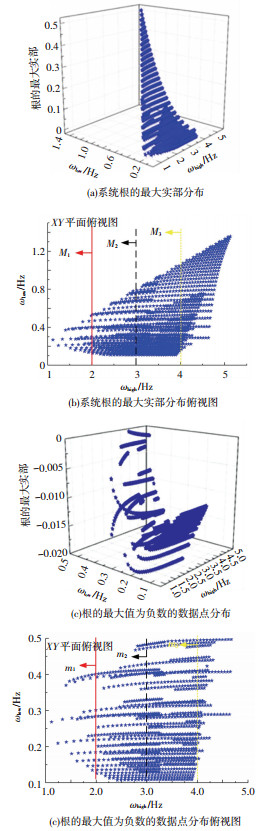
分析原理:1)设置模拟对象参数ms为103~104 kg,步长为103 kg;km为5~200 kN/m,步长为5 kN/m;kp为7~280 kN/m,步长为7 kN/m;me为500 kg;cm和cp由对接动力学阻尼比、质量和刚度参数求解;KV、ωn和ξ分别为10、63 Hz和0.3. 2)对每组系统参数求解对接动力学频率(ωlow, ωhig)作为x、y轴坐标,求解闭环传递函数根的实部sr的最大值并作为z轴坐标;3)由3D根轨迹法得到所有组的根的最大实部分布,分析系统能够模拟的动力学频率范围.
以对接动力学阻尼比ξ1=0.02和ξ2=0.02为例说明分析过程. 图 10(a)为所有组参数下系统闭环传递函数的根的最大实部分布图.最大实部为正值的情况多集中在动力学频率较大的区域,说明动力学频率越高,稳定性越差. 图 10(c)为图 10(a)中根的最大实部为负值的数据点. 图 10(b)和图 10(d)分别为图 10(a)和图 10(c)的XY俯视图,提取图 10(b)和图 10(d)中ωhigh<2、3和4 Hz的数据点,得到的数据点数目分别为M1、M2和M3及m1、m2和m3;用m1/M1,m2/M2和m3/M3表示ωhigh为2、3和4 Hz的稳定比率,定义稳定比率>95%时的对接动力学频率为保证稳定条件下系统对接动力学频率模拟能力.计算得η1=m1/M1=96.65%,η2=m2/M2=84.38%和η3=m3/M3=78.25%,则对接动力学频率模拟能力约为2 Hz,随着对接动力学频率增大,稳定比率快速下降.同理,令ξ1=0.05和ξ2=0.05,可得对接动力学频率为4.9 Hz的稳定比率为η=96.43%.随着阻尼比增大,系统能够模拟的ωhigh由2 Hz增大到4.9 Hz.在模拟参数范围内,ωhigh的最大值为5.2 Hz,为保证半物理仿真系统在模拟参数范围内稳定,则对接动力学阻尼比应不小于0.05.令对接动力学阻尼比为ξ1=0.1和ξ2=0.1,ωhigh为5.2 Hz的稳定比率为η=100%,说明半物理仿真系统在模拟对象的参数范围内均能稳定.
|
图 10 ξ1=0.02和ξ2=0.02的系统闭环传递函数的根的最大实部分布图 Fig. 10 Maximum real part distribution of the closed-loop transfer function of the system with ξ1=0.02 and ξ2=0.02 |
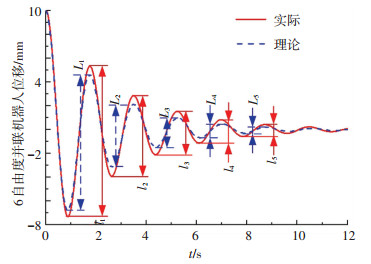
基于满足稳定要求的系统模拟能力结果, 进一步分析满足复现精度要求的系统模拟能力.以图 11所示的震荡位移曲线为例说明评定系统复现精度的标准.设图 4中航天器由初始位置(传感器不受力)偏移10 mm,即图 3中并联机器人偏移10 mm,然后进入动力学过程,并联机器人往复运动模拟图 4中航天器在对接机构作用下的运动.
|
图 11 系统复现精度原理 Fig. 11 Principle diagram of system reproduction precision |
将理论位移曲线(真实对接过程)与并联机器人的实际位移曲线对比,用式(5)计算半物理仿真系统的位移复现偏差.当对接动力学阻尼比为0.05左右时,经过几个震荡周期位移曲线就会趋于平稳,因此取前5个周期的震荡幅值计算复现偏差.
| $ \lambda=\left(\frac{l_{1}+l_{2}+l_{3}+l_{4}+l_{5}}{L_{1}+L_{2}+L_{3}+L_{4}+L_{5}}-1\right) \times 100 \%. $ | (5) |
根据式(5)进行多次仿真计算,得到了对接动力学阻尼比由0.02变化至0.10时,ωhigh的数值及其与并联机器人的频宽ωf的关系,如表 1所示.对接动力学阻尼比增大可以提高系统的动力学频率模拟能力,说明了阻尼比增大可以提高系统的稳定性和复现精度;而从图 12可知,动力学阻尼比增大到一定数值后,ωhigh增长明显变缓,这是因为并联机器人的频宽有限,复现过大的ωhigh会导致并联机器人幅值衰减过大,造成较大的精度损失. 表 1的数值关系为半物理仿真系统模拟对接过程的准确性和有效性提供理论依据.
| 表 1 动力学频率模拟能力仿真计算结果 Tab. 1 Calculation results of dynamics frequency simulation ability |
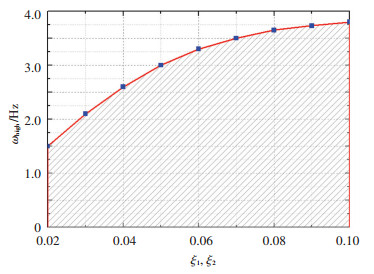
|
图 12 对接动力学频率模拟能力 Fig. 12 Docking dynamics frequency simulation ability |
仿真验证和实验验证中的初始条件均令图 3中并联机器人偏移10 mm,然后进入动力学过程,并联机器人往复运动模拟图 4中航天器在对接机构作用下的运动.
4.1 仿真验证应用MATLAB软件的Simulink模块搭建图 5和图 7所示的机械臂对接半物理仿真系统模型,验证第3节分析结果的正确性.仿真参数如表 2所示.参数组2-1用于对比机械臂为数学模型和六维弹簧机构的半物理仿真系统在高刚度接触时的稳定性;参数组2-2和2-3验证系统参数配置分析结果的正确性.参数组2-4和2-5验证半物理仿真系统对接动力学频率模拟能力分析结果的正确性.
| 表 2 仿真参数 Tab. 2 Simulation parameters |
仿真参数如表 2中参数组2-1所示,仿真结果如图 13所示.当接触刚度较大时,机械臂为数学模型的半物理仿真系统呈发散状态,发散曲线的震荡频率约等于并联机器人的固有频率.而机械臂为物理实物的半物理仿真系统为收敛状态.
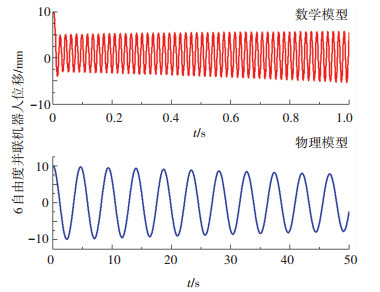
|
图 13 两种半物理仿真系统高刚度接触时的位移曲线 Fig. 13 Displacement of two HIL simulation systems with high stiffness contact |
表 2中参数组2-2满足式(2)的配置关系,表 2参数组中2-3不满足式(2)和(3).仿真结果如图 14和15所示.
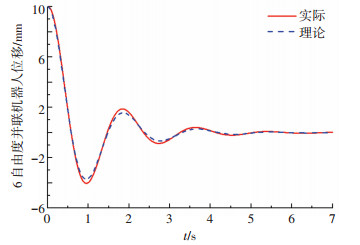
|
图 14 表 2中参数组2-2并联机器人位移曲线 Fig. 14 Displacement of the parallel robot with simulation parameters in Tab. 2-2-1 |

|
图 15 表 2中参数2-3并联机器人位移曲线 Fig. 15 Displacement of the parallel robot with simulation parameters in Tab. 2-2-3 |
高频振荡位移在阻尼作用下很快衰减,运动主要体现为低频振荡特性. 图 14中理论曲线和实际曲线高度重合,偏差率仅为2.5%(满足式(2)和(3)的参数配置通常能保证系统复现, 偏差率不高于5%). 图 15中理论曲线和实际曲线具有较大的偏差,偏差率达到27%,体现了3.2节参数配置分析结果的有效性.
4.1.3 半物理仿真系统动力学频率模拟能力结果验证以对接动力学阻尼比为ξ1=0.05, ξ2=0.05和表 2参数组中2-4为例进行仿真计算,仿真结果如图 16所示.
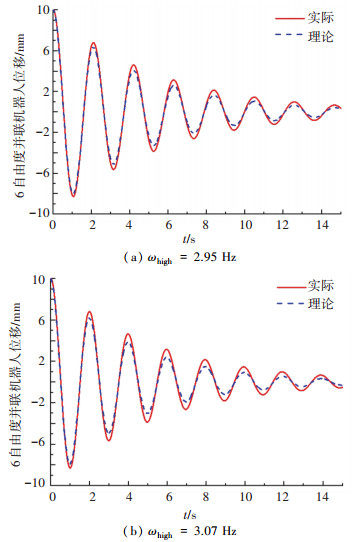
|
图 16 ξ1=0.05和ξ2=0.05的对接动力学频率模拟能力仿真验证 Fig. 16 Simulation verification of docking dynamics frequency simulation ability with ξ1=0.05 and ξ2=0.05 |
表 2中2-4仿真参数的高对接动力学频率ωhigh=2.95 Hz,ωhigh=0.325ωf,偏差率为8%;表 2中参数组2-5仿真参数的高对接动力学频率ωhigh=3.07 Hz,偏差率为12%.说明了表 1分析结果的正确性.
4.2 实验验证用一个已知刚度和阻尼的弹簧模拟末端执行器对目标适配器的作用,机械臂对接半物理仿真系统的主要实验设备见图 17.传感器下方装有六维弹簧机构和末端执行器,为模拟失重条件下的对接过程,实验前将传感器进行数值清零操作,去除机构重力对实验的影响.传感器仅测得接触力,并由对接动力学计算失重条件下的航天器运动,通过并联机器人复现运动过程.实验中,采用MATLAB的xPC模块作为实时仿真系统,采样时间为1 ms.实验参数为:km=70 kN/m, kp=7 kN/m;cm=1 kN/(m·s-1), cp=0.5 kN/(m·s-1), ms=103kg, me=135 kg.

|
图 17 机械臂对接半物理仿真系统实验设备 Fig. 17 Experimental setup for manipulator docking HIL simulation system |
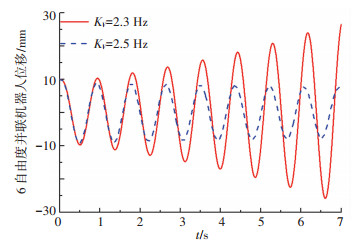
以半物理仿真系统满足中、低频段穿越为前提,得到了式(4)的稳定条件.以式(4)第3条为例,通过实验验证稳定条件的有效性.当KV=2.38 Hz时,系统为临界稳定.调整并联机器人的控制参数使得开环速度增益分别为KV=2.3 Hz(不满足稳定条件)和KV=2.5 Hz(满足稳定条件),得到的并联机器人位移曲线如图 18所示.由结果可知,KV稍小于临界值,则系统稳定,反之系统成发散状态;说明了稳定条件的有效性.
|
图 18 稳定条件验证 Fig. 18 Stability condition verification |
实验参数的动力学阻尼比约为ξ1=0.10和ξ2=0.11,得到的实验结果如图 19所示.

|
图 19 ξ1=0.10和ξ2=0.11的对接动力学频率模拟能力实验验证 Fig. 19 Experimental verification of docking dynamics frequency simulation ability with ξ1=0.10 and ξ2=0.11 |
当末端执行器质量由135 kg变为125 kg时(对接动力学阻尼比基本不变),对接动力学频率ωhigh由3.8 Hz增加到3.9 Hz,不满足表 1中的数值范围,偏差率由9.6%变为12%.实验结果、分析结果和仿真结果一致,说明了对接动力学频率模拟能力分析结果的正确性.
5 结论1) 针对机械臂为数学模型的机械臂对接半物理(HIL)仿真系统会因为对接机构的高接触刚度导致系统不稳定问题,提出了将机械臂等效为六维弹簧机构实物来模拟机械臂的对接过程.通过根轨迹法和实验分析验证了所提出的HIL仿真系统能够有效解决高刚度接触带来的不稳定现象,能够模拟高刚度的对接过程.
2) 机械臂对接HIL仿真系统的参数和接触环境复杂,为保证所提出的HIL仿真系统能够有效模拟对接过程,从3个重要方面对系统稳定性和复现精度进行了分析:应用系统-20 dB/dec段穿越理论得到了系统具有较好特性时系统参数的配置关系;应用稳定判据得到了HIL仿真系统的稳定条件;应用3D根轨迹法和仿真分析得到了系统对接动力学频率模拟能力.通过仿真和实验验证了所得结论的正确性,对空间对机械臂对接的可行性和准确性具有指导意义.
| [1] |
张凯锋, 周晖, 温庆平, 等. 空间站机械臂研究[J]. 空间科学学报, 2010, 30(6): 612. ZHANG Kaifeng, ZHOU Hui, WEN Qingping, et al. Review of the development of robotic manipulator for international space station[J]. Chinese Journal of Space Science, 2010, 30(6): 612. DOI:10.11728/cjss2010.06.612 |
| [2] |
张文辉, 叶晓平, 季晓明, 等. 国内外空间机器人技术发展综述[J]. 飞行力学, 2013, 31(3): 198. ZHANG Wenhui, YE Xiaoping, JI Xiaoming, et al. Development summarizing of space robot technology national and outside[J]. Flight Dynamics, 2013, 31(3): 198. |
| [3] |
ZENG D, YANG Y, CONG D, et al. Space End Effector Capturing Hybrid Simulation System[C]//2015 IEEE International Conference on Fluid Power and Mechatronics (FPM). Piscataway: IEEE Press, 2015: 448. DOI: 10.1109/FPM.2015.7337159 https://ieeexplore.ieee.org/document/7337159/
|
| [4] |
ZHAO H, ZHANG S. Stability research of space docking dynamics simulation based on Stewart platform[J]. Machine Tool & Hydraulics, 2006(8): 1. |
| [5] |
赵慧, 张尚盈. 空间对接整体动力学仿真系统稳定性分析[J]. 武汉科技大学学报(自然科学版), 2008, 31(1): 87. ZHAO Hui, ZHANG Shangying. Stability analysis of the whole dynamics simulation system of space docking[J]. Journal of Wuhan University of Science and Technology (Natural Science Edition), 2008, 31(1): 87. DOI:10.3969/j.issn.1674-3644.2008.01.020 |
| [6] |
ZEBENAY M, BOGE T, KRENN R, et al. Analytical and experimental stability investigation of a hardware-in-the-loop satellite docking simulator[J]. Journal of Aerospace Engineering, 2015, 229(4): 666. DOI:10.1177/0954410014539290 |
| [7] |
丰飞.空间大容差末端执行器及其软捕获策略研究[D].哈尔滨: 哈尔滨工业大学, 2013 FENG Fei. Research on space large misalignment tolerance end-effector and its soft capture strategy[D]. Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10213-1013045224.htm |
| [8] |
YANG H, XIE Z, SUN K, et al. Development of ground experiment system for space end-effector capturing the floating target in 3-dimensional space[J]. Industrial Robot: An International Journal, 2015, 42(4): 347. DOI:10.1108/IR-02-2015-0028 |
| [9] |
YANG H, JIN M, XIE Z, et al. Ground micro-gravity verification of free-floating non-cooperative satellite docking[C]//2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM). Piscataway: IEEE Press, 2015: 1253. DOI: 10.1109/AIM.2015.7222710 https://ieeexplore.ieee.org/document/7222710
|
| [10] |
QI C, GAO F, ZHAO X, et al. Low-order model based divergence compensation for hardware-in-the-loop simulation of space discrete contact[J]. Journal of Intelligent & Robotic Systems, 2017, 86(1): 81. DOI:10.1007/s10846-016-0460-y |
| [11] |
QI C, GAO F, ZHAO X, et al. A force compensation approach toward divergence of hardware-in-the-loop contact simulation system for damped elastic contact[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 2933. DOI:10.1109/TIE.2016.2643625 |
| [12] |
MA O, ZEBENAY M, BOGE T.Control of industrial robots for hardware-in-the-loop simulation of satellite docking[C]//International Society for Optics and Photonics-Sensors and Systems for Space Applications IV. San Francisco: SPIE Press, 2011: 80440G. DOI: 10.1117/12.886185
|
| [13] |
CHANG T, CONG D, YE Z, et al. Interface issues in hardware-in-the-loop simulation for spacecraft on-orbit docking[C]//2007 IEEE International Conference on Control and Automation. Piscataway: IEEE Press, 2007: 2584. https://ieeexplore.ieee.org/document/4376829
|
| [14] |
YAN H, HAN J, TONG Z, et al. Hybrid realtime simulation of the space docking process[C]//16th International Conference on Artificial Reality and Telexistence-Workshops. Piscataway: IEEE Press, 2006: 323. DOI: 10.1109/ICAT.2006.70 https://www.researchgate.net/publication/224281762_Hybrid_Realtime_Simulation_of_the_Space_Docking_Process
|
| [15] |
HUANG Q, JIANG H, ZHANG S, et al. Spacecraft docking simulation using hardware-in-the-loop simulator with Stewart platform[J]. Chinese Journal of Mechanical Engineering (English Edition), 2005, 18(3): 415. DOI:10.3901/CJME.2005.03.415 |
| [16] |
陈奎孚. 机械振动基础[M]. 北京: 中国农业大学出版社, 2011: 120. CHEN Kuifu. Principles of mechanical vibration[M]. Beijing: China Agricultural University Press, 2011: 120. |
 2019, Vol. 51
2019, Vol. 51


