仿猿双臂手机器人是一种模拟灵长类动物长臂猿悬臂摆荡动作的机器人,通过双臂交替摆荡、抓握树枝完成连续向前移动的运动.仿猿双臂手机器人属于一个欠驱动机械系统,具有二阶非完整约束及运动不可积的特点,这使其很难找到一条可行的运动轨迹实现可靠的连续移动.
对于仿生悬摆运动,Fukuda等[1]设计了BMR机器人,并完成了半个周期的连续移动实验. 2000年,吴伟国和Fukuda等[2]提出了具有多移动方式的类人猿机器人概念,并研制了Gorilla Robot Ⅰ机器人,此后Fukuda等继续设计了Gorilla Robot系列的Ⅱ、Ⅲ型机器人. 2002,年Kajima等[3]在Gorilla Robot Ⅱ机器人上完成了半个周期的连续运动控制. 2004年,Kajima等[4]在Gorilla Robot Ⅲ机器人上完成了3次的悬臂连续移动运动控制. Saito等[5-6]采用启发式学习方法生成摆荡运动前馈轨迹,并采用小脑神经网络进行运动的泛化. Nakanishi等[7]采用模型转化法进行连续摆荡抓杆运动控制. Lu等[8]采用分级控制方法设计了类人的多运动形式机器人运动切换控制器. Meghdari等[9]与Nakanishi等[10]均采用最优控制方法进行了连续移动实验,其中Nakanishi等在肘关节加入了具有柔顺控制及能量储存能力的变刚度驱动器,具有柔顺控制及能量储存的能力,增加了机器人抓杆范围.国内也有学者进行了相关理论研究,大多缺少实验验证.
赵旖旎等[11]设计了滑模变结构控制器并进行了实验,但在机器人上并未设计手爪,不能进行抓握桁架杆的动作.程红太等[12]通过分析仿猿双臂手机器人的悬臂飞跃过程,提出了基于虚约束的飞跃运动轨迹规划方法.
仿猿双臂手机器人现有的研究大多集中在悬摆动作的控制方法上,尚未见有对实验条件下摆荡抓杆的可靠性进行详细研究的论文.对此,借鉴猿猴摆荡抓杆前夕手爪与支撑杆间形成大阻尼的现象,吴伟国等[13]在2012年首次将大阻尼引入到仿猿双臂手机器人摇起抓杆的运动控制中,并在2018年提出了基于能量泵入法及大阻尼退转反馈的摇起抓杆控制策略,实现了仿真条件下的可靠摇起抓杆运动控制[14].与文献[14]中从单手握杆的竖直悬垂状态开始运动抓握目标杆不同,本文中双臂手机器人从两手均抓握桁架杆的状态开始,进行了连续多次摆荡渡越运动的仿真和实验研究,且本文提出了以重力势能最大为目标的机器人阶段性运动轨迹优化及其控制方法.
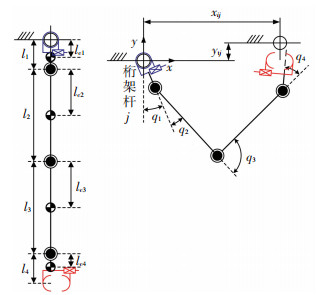
1 仿猿双臂手机器人系统简介 1.1 机器人机构及物理参数BARDAH-I型仿猿双臂手机器人如图 1所示,其各杆件参数示意图见图 2,机构参数如表 1所示,其中qi、mi、li、lci、Ji分别为关节i的角度、第i根杆的质量、长度、质心距离、转动惯量.双臂手完全展开成一条直线状态下,机器人两手爪中心的间距(臂展长度)约为1.44 m,总质量约9.33 kg.机器人有两个主动驱动的腕关节和一个主动驱动的肘关节(合计3-DOF),以及两个各由一个一体化伺服电动机驱动的开合手爪.

|
图 1 BARDAH-I型仿猿双臂手机器人 Fig. 1 BARDAH-I bionic-ape dual-arm hands robot |
|
图 2 机器人杆件参数示意 Fig. 2 Schematic diagram of robot mechanism parameters |
| 表 1 机器人机构参数 Tab. 1 Mechanism parameters of robot |
机器人手爪机构简图如图 3所示,夹持圆形断面杆的开合手爪的内表面贴有一层橡胶,使手爪与支撑杆之间能够提供较大的摩擦力矩.手爪上安装有MEMS陀螺仪及摩擦轮机构,用于检测欠驱动关节角度.摩擦轮机构通过增速机构连接光电编码器,两者皆用于检测欠驱动关节角度.

|
图 3 机器人手爪结构简图 Fig. 3 Diagram of robot gripper mechanism |
当开合手爪握住桁架杆时,手爪内表面的圆弧面与圆形断面杆构成可自由运动的回转副或有摩擦的回转副.虽然机器人本身没有欠驱动关节,但是,当手爪抓握杆件之后与环境构成了欠驱动关节.吴伟国等[13]2012年提出了大阻尼欠驱动的概念:当双臂手的一个手爪握住支撑杆,双臂手在单手悬挂状态下绕支撑杆中心回转,并带动另一个手爪向目标杆方向摆荡,当摆荡到可抓握区时,原本呈自由回转状态(小摩擦或假设为无摩擦)且还在向前摆荡的支撑手瞬间夹紧支撑杆,切换到阻止机器人绕支撑手退转的大阻尼状态,即称为大阻尼欠驱动.此处的欠驱动是指靠加大摩擦力阻止退转但并不能保证不退转,一旦退转则可由手爪上的退转反馈机构、陀螺仪同时检测退转角度和速度,并反馈给主动驱动关节控制器,控制主驱动关节快速驱动游动臂使游爪抓向目标杆.
1.3 机器人驱动系统构成BARDAH-I型仿猿双臂手机器人各关节直流伺服电机驱动采用Maxon公司的EPOS2-50/5直流伺服驱动器,具有运动控制器的功能.其中一个手爪采用EPOS2-50/5直流伺服驱动器,另一个手爪采用IPM100直流伺服驱动器.
上位机采用PC机,EPOS2驱动器与上位机间通过USB通信,各驱动器之间用CAN总线进行通信. IPM100驱动器用RS232与上位机相连,MEMS陀螺仪模块通过USB转串口模块与上位机通信.各驱动器能够返回各关节及手爪的位置信息.上位机的控制周期为40 ms,驱动器的控制周期为1 ms.根据各关节及手爪的位置及速度信息,上位机控制程序通过控制器的各运动阶段判别条件判断当前机器人的所在阶段,根据当前阶段激活对应的运动规划器.
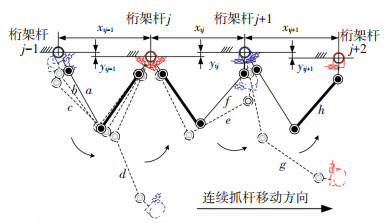
2 仿猿双臂手机器人连续抓杆移动运动优化与控制方法 2.1 双臂手连续交替抓杆移动的周期性运动仿猿双臂手控制目标为实现机器人在非连续介质(如桁架)上的连续移动.连续移动的一个周期为前后两臂交替移动各完成1次抓杆后,两臂的前后位置顺序得以恢复的过程,如图 4所示.文献[14]将仿猿双臂手机器人的一次抓杆运动分为以下几个阶段:调整阶段(a→b),松杆阶段(b→c),摆荡阶段(c→d→e),切换大阻尼(e),大阻尼抓杆阶段(e→f).当机器人游爪成功抓握目标杆后,双臂手两手爪都呈抓在杆上状态,完成一次完整的抓杆运动.若连续移动抓杆,则进入调整阶段,继续向前移动(f→g→h).在BARDAH-I型仿猿双臂手机器人的主驱动关节上采用PID控制,各主驱动关节控制律如下:
|
图 4 连续移动周期示意 Fig. 4 Schematic diagram of continuous movement cycle |
| $ \tau_{i}=K_{\mathrm{P}}\left(q_{i}^{\mathrm{d}}-q_{i}\right)+K_{1} \int\left(q_{i}^{\mathrm{d}}-q_{i}\right) \mathrm{d} t+K_{\mathrm{D}}\left(\dot{q}_{i}^{\mathrm{d}}-\dot{q}_{i}\right). $ | (1) |
式中:i=1, 2, 3;KP、KI、KD分别为比例系数、积分系数、微分系数.显然双臂手交替连续抓杆移动研究的核心是:解决由双手抓杆状态到空中游动再到手爪抓握住目标杆的运动分阶段生成和控制问题.连续抓杆运动不过是两手爪轮番进行抓握目标杆运动的不断重复.
设被机器人两手爪握住的分别是第j-1根和第j根桁架杆,下面分别对手爪完成单次抓杆运动的调整阶段的关节运动优化设计、松杆阶段的腕关节运动补偿、摆荡阶段的手爪末端轨迹优化、大阻尼抓杆阶段的手爪开合量及手爪位置修正进行分析,并给出关节轨迹生成方法和理论计算公式,以及各阶段间的运动切换条件式.切换条件理论上满足各阶段间运动的平滑切换,以防止切换时产生震颤,相当于滑模变结构控制.
2.2 调整阶段使重力势能最大化自运动构形获得调整阶段机器人的初始状态为两手均抓握桁架杆的状态,需调整机器人构形使其在松杆后具有足够摆荡至下一根目标杆可抓握区的能量.这里以重力势能为目标函数,优化得到重力势能最大的机器人构形作为调整阶段的目标构形.
机器人的重力势能EV为
| $ {E_{\rm{V}}} = \sum\limits_{i = 1}^4 {{A_i}} \cos \left( {{q_1} + {q_2} + \cdots + {q_i}} \right). $ | (2) |
式中:Ai为根据机器人参数确定的常量,计算式见文献[15]中的公式(2-14).由于调整阶段内机器人与所抓握的桁架杆构成平面5杆机构,其运动自由度共有2个,因此机器人3个主动关节角q2、q3、q4和欠驱动关节角q1中只有2个自由变量,这里选择腕关节转角q2和q4作为调整阶段机器人构形优化的设计变量,目标函数EV中的欠驱动关节转角q1和肘关节转角q3分别为
| $ q_{1}=0.5 \pi-\sin ^{-1}\left(\frac{l_{2}}{l_{13}} \sin q_{2}\right)-\cos ^{-1}\left(\frac{l_{13}^{2}+l_{15}^{2}-l_{35}^{2}}{2 l_{13} l_{15}}\right), $ | (3) |
| $ \begin{aligned} q_{3}=& \pi-\sin ^{-1}\left(\frac{l_{1}}{l_{13}} \sin q_{2}\right)-\cos ^{-1}\left(\frac{l_{13}^{2}-l_{15}^{2}+l_{35}^{2}}{2 l_{13} l_{35}}\right)-\\ & \sin ^{-1}\left(l_{4} / l_{35} \sin q_{4}\right). \end{aligned} $ | (4) |
式中:l13、l35、l15分别是起始杆到肘关节、肘关节到支撑杆、起始杆到支撑杆的距离,且
| $ l_{13}=\sqrt{l_{1}^{2}+l_{2}^{2}-2 l_{1} l_{2} \cos q_{2}}, $ | (5) |
| $ l_{35}=\sqrt{l_{3}^{2}+l_{4}^{2}-2 l_{3} l_{4} \cos q_{4}}. $ | (6) |
l15根据杆间距参数确定.将式(3)~(6)代入式(2),可得关于两个腕关节转角的目标函数EV=EV(q2, q4).调整阶段的机器人构形优化问题可用式(7)中的数学模型表达,求解此优化模型可以得到机器人最优构形的两个腕关节角,分别记作q2f、q4f.
| $ \begin{array}{c} \mathop {\max }\limits_{{q_2}, {q_4}} {E_{\rm{V}}}\left( {{q_2}, {q_4}} \right), \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{q_{2\min }} \le {q_2} \le {q_{2\max }}, {q_{4\min }} \le {q_4} \le {q_{4{\rm{max}}}}. \end{array} $ | (7) |
上述最优构形的肘关节角以q3f表示,将q2=q2f、q4=q4f代入式(4)可计算得到q3f.在进行调整阶段的机器人运动控制时,若同时对q2、q3、q4按式(1)所示控制律进行控制,则由于存在机构参数误差和控制误差,可能使机器人在调整阶段形成的两自由度五杆闭链机构的3个主动关节运动发生干涉,因此这里按式(8)来规划两个腕关节的运动轨迹并进行轨迹追踪控制,使肘关节的伺服电机在调整阶段处于电流为0的自由运动状态.
| $ q_{i}^{\mathrm{d}}=q_{i}^{0}+a_{\mathrm{cp}}\left(q_{i}^{\mathrm{f}}-q_{i}^{0}\right) $ | (8) |
式中i=2, 4;qid为发送给关节PID控制器的关节角给定位置;qi0为当前运动阶段开始时的第i个关节的角度;acp为调整阶段过渡系数
| $ a_{\mathrm{cp}}=0.5\left[1-\cos \left(\pi t_{\mathrm{cp}} / T_{\mathrm{cp}}\right)\right]. $ |
式中:tcp为从调整阶段开始进行计时得到的系统时间,Tcp为调整阶段的运行时间.为保证各关节角速度在限制范围内,Tcp需满足
| $ {{\dot q}_{{\rm{ }}i{\rm{min }}}} \le \dot q_i^{\rm{d}}\left( {{T_{{\rm{cp}}}}/2} \right) \le {{\dot q}_{{\rm{ }}i\max {\rm{ }}}}, \quad i = 2, 3, 4. $ |
其中两个腕关节的角速度由式(8)中的目标位置差分得到,肘关节角速度为
| $ \dot q_3^{\rm{d}} = - \left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right] \cdot {\left[ {\begin{array}{*{20}{c}} {{C_1}}&{{C_3}}\\ {{S_1}}&{{S_3}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{C_2}}&{{C_4}}\\ {{S_2}}&{{S_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot q_2^{\rm{d}}}\\ {\dot q_4^{\rm{d}}} \end{array}} \right]. $ |
其中
| $ \begin{array}{c} {C_i} = \sum\limits_{j = 1}^{5 - i} {{l_j}} \cos \left( {{q_1} + {q_2} + \cdots + {q_j}} \right), \\ {S_i} = - \sum\limits_{j = 1}^{5 - i} {{l_j}} \sin \left( {{q_1} + {q_2} + \cdots + {q_j}} \right), i = 1, 2, 3, 4. \end{array} $ |
切换条件:调整阶段结束
| $ q_{i}=q_{i}^{\mathrm{f}} \& \dot{q}_{i}=0. $ |
松杆阶段的控制目标为通过主动关节的运动,使手爪完全脱离起始杆.若即将变成游动状态的手爪在松杆过程中勾住起始杆,只需对腕关节进行补偿,使手爪开口中心与支撑杆中心重合即可,补偿角度为
| $ \Delta q_{4}=\arctan \left(d / 2 l_{4}\right). $ |
式中d为支撑杆的直径.处于松杆过程中的手爪的腕关节(如图 2中q4)目标位置为
| $ q_{4}^{\mathrm{f}}=q_{4}-\Delta q_{4}. $ |
各主驱动关节运动轨迹如下:
| $ \begin{array}{c}{q_{i}^{\mathrm{d}}=q_{i}^{0}, \quad i=2, 3}; \\ {q_{4}^{\mathrm{d}}=q_{4}^{0}+a_{\ln }\left(q_{4}^{\mathrm{f}}-q_{4}^{0}\right)}.\end{array} $ |
其中alh为松杆阶段过渡系数,且
| $ a_{\mathrm{lh}}=\left\{\begin{array}{ll}{0.5\left[1-\cos \left(\pi t_{\mathrm{lh}} / T_{\mathrm{lh}}\right)\right], } & {t_{\mathrm{lh}} \leqslant T_{\mathrm{lh}}}; \\ {1, } & {t_{\mathrm{lh}}>T_{\mathrm{lh}}}.\end{array}\right. $ |
式中:tlh为从松杆阶段开始进行计时得到的系统时间,Tlh为松杆阶段的运行时间.
切换条件:机器人欠驱动关节角速度
| $ \left|\dot{q}_{1}\right| \geqslant \dot{q}_{1}^{*}. $ |
当肘关节角q3处于0°附近时,肘关节运动对欠驱动关节影响更大.仿真发现,若肘关节在欠驱动关节之前到达0°位置,则能使欠驱动关节最终摆荡到更大的角度.根据上述励振摆荡原理,肘关节角加速度按式(9)计算时,可增大欠驱动关节的摆幅,积分得肘关节角速度为式(10),期望参考轨迹为式(11).
| $ {\ddot q_3} = \left\{ {\begin{array}{*{20}{l}} {{a_{3\max }}\sin \left( {\pi t/{T_1}} \right), }&{t \le {t_1};}\\ {0, }&{{t_1} < t \le {t_2};}\\ { - {a_{3\max }}\sin \left[ {\pi \left( {t - {t_2}} \right)/{T_3}} \right], }&{{t_2} < t \le {t_3};}\\ {0, }&{t > {t_3}.} \end{array}} \right. $ | (9) |
| $ {\dot q_3} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{v_{3\max }}}}{2}\left[ {1 - \cos \left( {\pi t/{T_1}} \right)} \right], }&{t \le {t_1};}\\ {{v_{3\max }}, }&{{t_1} < t \le {t_2};}\\ {\frac{{{v_{3\max }}}}{2}\left[ {\cos \left[ {\pi \left( {t - {t_2}} \right)/{T_3}} \right] + 1} \right], }&{{t_2} < t \le {t_3};}\\ {0, }&{t > {t_3}.} \end{array}} \right. $ | (10) |
| $ q_3^{\rm{d}} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {q_3^0 + \frac{{{v_{3\max }}t}}{2} - \frac{{{v_{3\max }}}}{2}\sin \left( {\frac{{\pi t}}{{{T_1}}}} \right)\frac{{{T_1}}}{\pi }, }&{t \le {t_1};}\\ {q_3^0 + {v_{3\max }}{T_1}/2 + {v_{3\max }}\left( {t - {t_1}} \right), }&{{t_1} < t \le {t_2};}\\ \begin{array}{l} q_3^0 + {v_{3\max }}\left( {{T_1}/2 + {T_2}} \right) + \left( {{v_{3\max }}/2} \right)\\ \left( {t - {t_2}} \right) + \frac{{{v_{3\max }}}}{2}\sin \left[ {\frac{{\pi \left( {t - {t_2}} \right)}}{{{T_3}}}} \right]\frac{{{T_3}}}{\pi }, \end{array}&{{t_2} < t \le {t_3};}\\ {q_3^{\rm{f}}, }&{t > {t_3}.} \end{array} \end{array} \right. $ | (11) |
肘关节轨迹各段时间间隔为T1=t1,Ti=ti-ti-1,i = 2, 3.通过给定肘关节目标位置q3f、初始位置q30、最大加速度a3max、最大减速a3min、最大速度v3max,则
| $ \begin{aligned} T_{1} &=0.5 \pi v_{3 \mathrm{max}} / a_{3 \mathrm{max}}, \\ T_{3} &=0.5 \pi v_{3 \mathrm{max}} / a_{3 \mathrm{min}}, \\ T_{2} &=\left(q_{3}^{\mathrm{f}}-q_{3}^{0}\right)+0.5\left(T_{3}-T_{1}\right). \end{aligned} $ |
根据上述肘关节轨迹,将摆荡阶段肘关节的最大加速度a3max、最大减速度a3min、最大速度v3max作为优化设计变量,使肘关节运动轨迹尽可能满足以下要求:肘关节角速度需在机器人的角速度限制范围内;在手爪最接近目标位置时,手爪与目标杆间的距离尽可能近;在达到距离目标位置最近的时刻,手爪移动速度尽可能小.考虑以上3个方面,可分别定义3个评价指标:肘关节角速度极限评价函数J1、距离评价函数[13]J2;速度评价函数[13]J3为
| $ \begin{array}{c} {J_1} = \max \left[ {\left( {{q_3} - {q_{3\min }}} \right)/\left( {{q_{3\max }} - {q_{3\min }}} \right)} \right], \\ {J_2} = \min \left( {\sqrt {{{\left( {{x_{\rm{h}}} - {x_{{\rm{ target }}}}} \right)}^2} + {{\left( {{y_{\rm{h}}} - {y_{{\rm{ target }}}}} \right)}^2}} } \right), \\ {J_3} = \left\| {\mathit{\boldsymbol{v}}_{\rm{h}}^*} \right\|. \end{array} $ |
式中:xh、yh为游手中心的横纵坐标,xtarget、ytarget为目标杆的横纵坐标,vh*为游手距离目标杆最近时的速度矢量.综合上述3个评价指标,摆荡阶段肘关节运动轨迹的优化模型为
| $ \begin{array}{c} \mathop {\min }\limits_{{a_{3\max }}, {a_{3\min }}, {v_{3\max }}} \cdot J = {J_1} + {J_2} + {J_3}, \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{{\ddot q}_{3\min }} \le {a_{3\max }} \le {{\ddot q}_{3\max }}, {{\ddot q}_{3\min }} \le {a_{3\min }} \le {{\ddot q}_{3\max }}, \\ {{\dot q}_{3\min }} \le {v_{3\max }} \le {{\dot q}_{3\max }}. \end{array} $ |
式中:
| $ \begin{array}{c}{q_{2}^{\mathrm{d}}=0}, \\ {q_{4}^{\mathrm{d}}=q_{4}^{0}+a_{4 {\rm s}}\left(q_{4}^{\mathrm{f}}-q_{4}^{0}\right)}.\end{array} $ |
其中a4s为腕关节的过渡系数,且
| $ {a_{{\rm{4s}}}} = \left\{ {\begin{array}{*{20}{l}} {0.5\left[ {1 - \cos \left( {\pi {t_{\rm{s}}}/{T_{4{\rm{s}}}}} \right)} \right], }&{{t_{\rm{s}}} \le {T_{4{\rm{s}}}};}\\ {1, }&{{t_{\rm{s}}} > {T_{4{\rm{s}}}}.} \end{array}} \right. $ |
式中:ts为从摆荡阶段开始进行计时得到的系统时间,T4s为腕关节位置调整时间.
在欠驱动关节摆向目标杆方向的角速度为0且能量达到目标角度能量时(即满足式(12)时),
| $ \left\{ {\begin{array}{*{20}{l}} {{q_1} > 0, }\\ {{{\dot q}_1} = 0, }\\ {{E_{\rm{t}}} > {E^{\rm{d}}}.} \end{array}} \right. $ | (12) |
支撑手爪与支撑杆之间形成大阻尼,降低欠驱动关节向后退转的速度,方便实现抓杆动作.切换条件:在满足式(12)的基础上,当满足式(13)时, 进入到大阻尼抓杆阶段.此切换条件表示进入抓杆阶段的时机为关节角达到目标位置且运动停止的时刻,这样能够减少切换带来的冲击.
| $ q_{i}=q_{i}^{\mathrm{f}} \& \dot{q}_{i}=0, \quad i=2, 3, 4. $ | (13) |
为避免手爪与目标杆发生碰撞,抓杆阶段分两步完成.根据手爪张开的大小,将逆运动学计算中使用的目标杆位置修正为
| $ \left\{\begin{array}{l}{x_{\mathrm{d}}=x_{\mathrm{t} j}+0.5 Nh_{\mathrm{m}}} \\ {y_{\mathrm{d}}=y_{\mathrm{t}j}}.\end{array}\right. $ |
式中:(xtj, ytj)为第j+1根桁架杆相对于第j根桁架杆的位置坐标;hm为手爪张开最大距离;为使手爪勾住目标杆,N在抓杆的两步中分别取
| $ N=\left\{\begin{aligned}-1, & t_{\mathrm{cb}} \leqslant t_{\mathrm{ch} 1}; \\ 0, & t_{\mathrm{cbl}}<t_{\mathrm{cb}} \leqslant t_{\mathrm{cb} 2}. \end{aligned}\right. $ |
逆运动学计算式为
| $ \left[ {\begin{array}{*{20}{l}} {q_2^{\rm{f}}}\\ {q_3^{\rm{f}}}\\ {q_4^{\rm{f}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\frac{\pi }{2} - {{\cos }^{ - 1}}\left( {\frac{{l_1^2 + l_{24}^2 - l_{14}^2}}{{2{l_1}{l_{24}}}}} \right) + {{\cos }^{ - 1}}\left( {\frac{{l_2^2 + l_3^2 - l_{24}^2}}{{2{l_2}{l_3}}}} \right)}\\ {\frac{\pi }{2} - {{\cos }^{ - 1}}\left( {\frac{{l_2^2 + l_3^2 - l_{24}^2}}{{2{l_2}{l_3}}}} \right)}\\ {\frac{\pi }{2} - {{\cos }^{ - 1}}\left( {\frac{{l_4^2 + l_{24}^2 - l_{25}^2}}{{2{l_4}{l_{24}}}}} \right) + {{\cos }^{ - 1}}\left( {\frac{{l_2^2 + l_3^2 - l_{24}^2}}{{2{l_2}{l_3}}}} \right)} \end{array}} \right]. $ | (14) |
其中:
| $ \begin{array}{l}{l_{24}=\sqrt{\left(l_{1} \sin q_{1}-x_{\mathrm{d}}\right)^{2}+\left(l_{1} \cos q_{1}-y_{\mathrm{d}}+l_{4}\right)^{2}}}. \\ {l_{25}=\sqrt{\left(l_{1} \sin q_{1}-x_{\mathrm{d}}\right)^{2}+\left(l_{1} \cos q_{1}-y_{\mathrm{d}}\right)^{2}}}.\end{array} $ |
根据式(14)及欠驱动关节反馈实时计算各关节目标角度,则各关节的目标轨迹为
| $ \left\{\begin{array}{l}{q_{2}^{\mathrm{d}}=a_{\mathrm{cl}} q_{2}^{\mathrm{f}}}, \\ {q_{i}^{\mathrm{d}}=q_{i}^{0}+a_{\mathrm{cl}}\left(q_{i}^{\mathrm{f}}-q_{i}^{0}\right), i=3, 4}.\end{array}\right. $ |
其中ac1为过渡系数,且
| $ a_{\mathrm{cl}}=\left\{\begin{array}{ll}{0.5\left[1-\cos \left(\pi t_{\mathrm{c}} / T_{\mathrm{cl}}\right)\right], } & {t_{\mathrm{c}} \leqslant T_{\mathrm{cl}}}; \\ {0.5\left[1-\cos \left(\pi\left(t_{\mathrm{c}}-T_{\mathrm{cl}}\right) / T_{\mathrm{c} 2}\right)\right]}, & T_{\mathrm{cl}}{ \leqslant t_{\mathrm{c}} \leqslant T_{\mathrm{c} 2}};\\ {1, } & {t_{\mathrm{c}}>T_{\mathrm{c} 2}}.\end{array}\right. $ |
式中:tc为从抓杆阶段开始进行计时得到的系统时间,Tc1抓杆阶段1总时间,Tc2为抓杆阶段2总时间.
切换下一阶段条件:游手闭合
| $ h_{y}=0 \& \dot{h}_{y}=0. $ |
式中hy为游动手爪的开合距离.
在欠驱动关节切换大阻尼后,进入到抓杆阶段,采用大阻尼退转反馈实现稳定的抓杆,为此,欠驱动关节退转速度及欠驱动关节摩擦力矩需满足抓杆稳定性条件,当不满足抓杆稳定性条件时,即当判断条件式
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot q}_1} > \sum\limits_{k = 2}^4 {\frac{{{K_k}{{\dot q}_k}}}{{{x_4}{y_{\rm{d}}} - {x_{\rm{d}}}{y_4}}}, } }\\ {{\tau _i} > {\tau _{i\max }}.} \end{array}} \right. $ |
成立时[14],需要采用文献[14]中的励振方法,重新励振即退回到摆荡阶段,再次摆荡到可抓握区并切换至大阻尼欠驱动抓杆状态实施二次抓握目标杆.
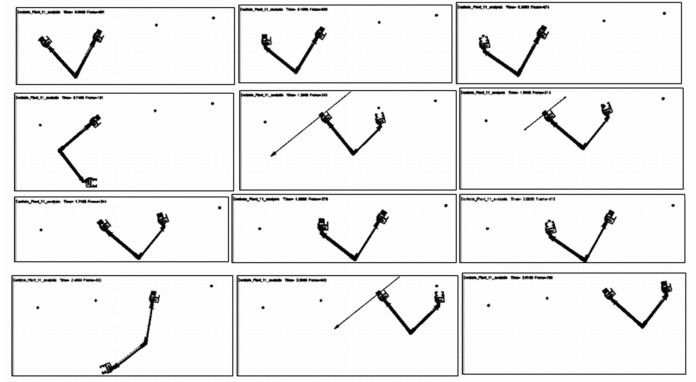
3 连续交替抓杆移动仿真与运动控制实验 3.1 连续交替抓杆移动运动样本生成实例与仿真4根桁架杆的坐标分别为(-0.8, -0.1)、(0, 0)、(0.8, 0.1)、(1.6, 0.2) m.利用前述方法分别对相邻桁架杆间的摆荡抓杆运动进行轨迹优化与样本生成,而后以ADAMS-Matlab/Simulink进行BARDAH机器人的连续移动联合仿真,手爪与支撑杆的接触参数见表 2,视频截图如图 5所示.
| 表 2 手爪与支撑杆间接触参数设置 Tab. 2 Contact parameters between gripper and bar |
|
图 5 仿猿双臂手机器人连续移动仿真视频截图 Fig. 5 Continuous mobile simulation video screenshot of bionic-ape dual-arm hands robot |
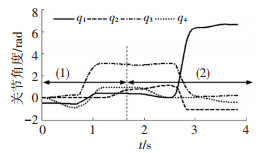
仿猿双臂手机器人连续移动仿真各关节轨迹如图 6所示.
|
图 6 连续移动仿真各关节轨迹 Fig. 6 Continuously moving simulation of joint trajectories |
其中(1)为连续移动的前半个周期,(2)为后半个周期.第一次移动用时1.7 s,第二次移动用时为2.3 s.仿真结果表明,所提出的关节运动轨迹优化以及运动控制方法能够使仿猿双臂手机器人完成多根桁架杆之间的连续移动,同时也通过仿真验证了该机器人的驱动能力,为连续交替抓握目标杆的运动控制实验提供了可行性验证和仿真数据依据.
3.2 双手交替连续抓杆移动控制实验与结果分析对本文提出的方法进行了实验验证,实验中机器人抓握的起始杆和目标杆位于同一水平高度,起始杆与中间杆的间距为1.0 m,中间杆与目标杆间距分别选为0.5、0.6、0.7、0.8 m.针对每个目标杆间距,首先,按第2节中提出的优化方法生成不同运动调整阶段、松杆阶段和摆荡阶段的最优运动样本,并对机器人关节的PID轨迹追踪控制器进行参数整定;而后,通过与3.1小节中相同的步骤进行仿真,验证机器人的驱动能力.上述准备完成后,对每个目标杆间距进行了3组实验,共进行了12组实验.
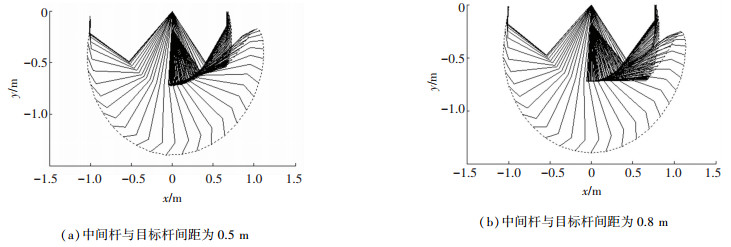
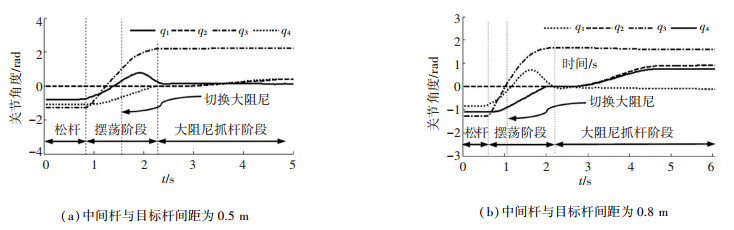
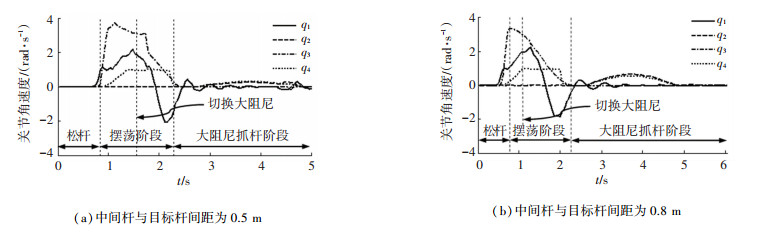
图 7给出了中间杆与目标杆间距分别为0.5 m和0.8 m情况下的机器人运动轨迹,图 8、9分别给出了对应的机器人关节角和角速度曲线.由图 9可知,摆荡阶段欠驱动关节速度先迅速增加,后缓慢降低,利用了主驱动关节与欠驱动关节的耦合关系.对应中间杆与目标杆间距分别为0.5 m和0.8 m两种情况,实验的视频截图分别如图 10、11所示.
|
图 7 中间杆与目标杆间距分别为0.5 m和0.8 m时的机器人运动轨迹 Fig. 7 Robot trajectory when the distance between the middle rod and the target rod is 0.5 m and 0.8 m respectively |
|
图 8 中间杆与目标杆间距分别为0.5 m和0.8 m时各关节角度曲线 Fig. 8 Joint angle curve when the distance between the middle rod and the target rod is 0.5 m and 0.8 m respectively |
|
图 9 中间杆与目标杆间距分别为0.5 m和0.8 m时的关节角速度曲线 Fig. 9 Joint angular velocity curve when the distance between the middle rod and the target rod is 0.5 m and 0.8 m respectively |

|
图 10 中间杆与目标杆间距为0.5 m时机器人摆荡抓杆控制实验视频截图 Fig. 10 Video of the robot swinging grab control experiment when the distance between the middle rod and the target rod is 0.5 m |

|
图 11 中间杆与目标杆间距为0.8 m时机器人摆荡抓杆控制实验视频截图 Fig. 11 Video of the robot swinging grab control experiment when the distance between the middle rod and the target rod is 0.8 m |
图 10中,摆荡阶段内欠驱动关节能够达到的最大角度为44°左右,由于摩擦力矩不足以完全抵消重力矩及惯性力矩,机器人向后退转了35°左右.由于手爪与支撑杆之间有一定的距离,机器人从开始切换大阻尼到完全切换到大阻尼需要一定的时间,为使欠驱动关节在退转后能够稳定到一个比较高的角度,需要提前切换大阻尼.由图 11可知机器人在抓杆后腕关节角度较大,当超过关节极限时,会导致抓杆失败.当抓杆失败时,采用文献[14]的从垂吊状态摇起抓杆控制策略进行再次摆荡抓杆.对中间杆与目标杆间距为0.5~0.8 m的全部12次实验的统计结果如表 3所示.
| 表 3 中间杆与目标杆间距分别为0.5~0.8 m实验统计结果 Tab. 3 Results of the experiment when the distance between the middle rod and the target rod is 0.5~0.8 m respectively |
从表 3中可以看出,机器人在摆荡阶段能够摆荡较高的角度,当抓较远距离的目标杆时,由于重力矩较大,机器人的退转角度较大.在实验中发现,以靠近支撑手爪的腕关节进行退转补偿,当腕关节到达关节极限时会导致抓杆失败,但通过调整阶段的构形重力势能优化,机器人在切换大阻尼时其欠驱动关节能达到较高的摆角,此问题得以解决.实验证明,大阻尼方法在可抓握范围内能够100%的成功抓杆.
本文提出的抓杆移动轨迹优化方法、分阶段控制方法及连续抓杆移动控制实验的部分内容已申请发明专利[16]并被受理.
4 结论1) 提出了为获得重力势能最大化构形的调整阶段机构自运动优化、摆荡阶段肘关节轨迹优化、抓杆阶段采用大阻尼退反馈方法等的关节运动轨迹生成方法,并进行了各阶段控制器设计.
2) 利用提出的方法、设计的分阶段控制器和ADAMS-Simulink软件进行联合仿真,仿真实现了在不同高度的多根目标杆环境下,仿猿双臂手机器人连续抓杆移动,表明控制方法能够实现交替抓握不同高度目标杆的连续移动.
3) 使用臂展长度为1.44 m的仿猿双臂手机器人,在起始杆与中间杆间距为1 m,中间杆与目标杆间距分别为0.5、0.6、0.7、0.8 m的3根杆环境下,进行了12组连续交替抓杆移动运动控制实验,实验表明,提出的运动优化与大阻尼欠驱动控制方法能够实现成功率为100%的可靠连续抓杆移动.
| [1] |
FUKUDA T, SAITO F. Motion control of a brachiation robot[J]. Robotics & Autonomous Systems, 1996, 18(1): 83. DOI:10.1016/0921-8890(96)00002-4 |
| [2] |
WU Weiguo, HASEGAWA Y, FUKUDA T. Gorilla robot mechanism design and basic research of standing up action[C]// 18th Annual Conference of the Robotics Society of Japan (RSJ). Tokyo: The Robotics Society of Japan, 2000: 1455.
|
| [3] |
KAJIMA H, HASEGAWA Y, FUKUDA T, et al. Study on brachiation controller-adjustment method of strength and timing parameters[C]// Intelligent Robots and Systems. Lausanne: IEEE, 2002: 2497. DOI: 10.1109/IRDS.2002.1041644 https://ieeexplore.ieee.org/document/1041644
|
| [4] |
KAJIMA H, DOI M, HASEGAWA Y, et al. A study on a brachiation controller for a multi-locomotion robot: Realization of smooth, continuous brachiation[J]. Advanced Robotics, 2004, 18(10): 1025. DOI:10.1163/1568553042674671 |
| [5] |
SAITO F, FUKUDA T, ARAI F. Swing and locomotion control for a two-link brachiation robot[J]. Control Systems IEEE, 1994, 14(1): 5. DOI:10.1109/37.257888 |
| [6] |
SAITO F, FUKUDA T, ARAI F, et al. Heuristic generation of driving input and control of brachiation robot[J]. JSME International Journal, 1994, 37(1): 147. DOI:10.1299/jsmec1993.37.147 |
| [7] |
NAKANISHI J, FUKUDA T, KODITSCHEK D E. A brachiating robot controller[J]. IEEE Tranctions on Robotics & Automation, 2000, 16(2): 109. DOI:10.1109/70.843166 |
| [8] |
LU Z G. Motion transfer control from walking to brachiation through vertical ladder climbing for a multi-locomotion robot[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(5): 1681. DOI:10.1109/TMECH.2013.2292327 |
| [9] |
MEGHDARI A, MOHAMMAD H S, NOROUZI L M, et al. Minimum control effort trajectory planning and tracking of the CEDRA brachiation robot[J]. Robotica, 2013, 31(7): 1119. DOI:10.1017/S0263574713000362 |
| [10] |
NAKANISHI J, RADULESCU A. Spatio-temporal stiffness optimization with switching dynamics[J]. Autonomous Robots, 2017, 41(2): 273. DOI:10.1007/s10514-015-9537-x |
| [11] |
赵旖旎, 程红太, 张晓华. 基于动态伺服的欠驱动双摆机器人仿生悬摆控制[J]. 机器人, 2009, 31(4): 1. ZHAO Yini, CHENG Hongtai, ZHANG Xiaohua. Life-like brachitaion control of underactuated two-link robot based on dynamical servo[J]. ROBOT, 2009, 31(4): 1. DOI:10.13973/j.cnki.robot.2009.04.007 |
| [12] |
WAN D K, CHENG H I, JI G F, et al. Non-horizontal ricochetal brachiation motion planning and control for two-link Bio-primate robot[C]//IEEE International Conference on Robotics and Biomimetics. Zhuhai: IEEE, 2015: 19. DOI: 10.1109/ROBIO.2015.7407033 http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-DBDX201702004.htm
|
| [13] |
吴伟国, 席宝时. 三自由度欠驱动机器人抓握目标杆运动控制[J]. 哈尔滨工业大学学报, 2013, 45(11): 26. WU Weiguo, XI Baoshi. Motion control for 3-DOF underactuated robot to grasp objective rod[J]. Journal of Harbin Institute of Technology, 2013, 45(11): 26. DOI:10.11918/j.issn.0367-6234.2013.11.005 |
| [14] |
WU W G, HUANG M C, GU X D. Underactuated control of bionic-ape robot based on the energy pumping method and big damping condition turn-back angle feedback[J]. Robotics & Autonomous Systems, 2018, 100(2): 119. DOI:10.1016/j.robot.2017.11.006 |
| [15] |
李海伟.仿猿双臂手机器人连续移动控制及实验研究[D].哈尔滨: 哈尔滨工业大学, 2018. LI Haiwei. Research on continuous brachiation control and experiment of a bionic-ape dual-arm hands robot[D]. Harbin: Harin Institute of Technology, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10213-1018892495.htm |
| [16] |
吴伟国, 高力扬.能摆荡抓握远距离桁架杆的攀爬桁架机器人及其控制方法: 201811098860.8 [P]. (已受理) WU Weiguo, GAO Liyang.Climbing truss robot capable of grasping long-distance truss rod and its control method: 201811098860.8 [P]. (Application accepted) |
 2019, Vol. 51
2019, Vol. 51



