2. 沈阳航空航天大学 机电工程学院, 沈阳 110136;
3. 沈阳发动机研究所, 航空发动机动力传输航空科技重点实验室(中国航发)沈阳 110015
2. School of Mechatronics Engineering, Shenyang Aerospace University, Shenyang 110136, China;
3. Shenyang Engine Research Institute, Key Laboratory of Power Transmission Technology on Aero-engine (Aero Engine Corporation of China), Shenyang 110015, China
齿轮传动广泛应用于船舶、航空航天及风力发电等领域,齿轮系统的动力学特性将直接影响机械结构的安全性和可靠性.最近几年来,国内外学者对齿轮系统动力学等内容开展了深入的研究[1-2]. Kahraman等[3-4]建立了单自由度直齿轮非线性动力学模型,考虑周期时变刚度的影响,用数值法得到了系统的动力学特性. Chen等[5]推导了齿轮中心距误差与齿隙之间的关系,定义了动态齿隙,并对计及动态间隙、摩擦和时变刚度的多自由度非线性动态齿轮传动系统进行了研究. Wu等[6]建立了复合行星齿轮非线性动力学模型,讨论了因磨损导致的齿侧间隙变化对系统的影响.
在以往研究中,因研究条件限制而忽略由制造误差和磨损润滑等造成的不确定性因素,但由于上述因素对系统响应有重要的影响,学者们开始重视对不确定性因素的研究[7].王靖岳等[8]通过正态分布规律来描述啮合刚度的不确定性,并运用4阶Runge-Kutta数值积分法对三自由度直齿轮副系统的稳定性问题进行了分析和研究.廖映华等[9]则在啮合刚度的确定性表达式中增加随机分量,通过服从截尾正态分布规律的随机变量描述其随机不确定性.冯松等[10]根据Timoshinko梁理论,分析和计算了点蚀和磨损情况下的齿轮啮合刚度以及其发展规律,但只是分析了刚度,并没有研究刚度对于整个齿轮-轴承系统的动力学特性的影响.陈奇等[11]引入可用于接触强度分析的M-B分形接触新理论模型,建立两粗糙曲面的分形接触模型,为利用分形接触模型研究齿轮接触动力学提供了参考.
基于考虑齿侧间隙的齿轮-轴承系统模型[12],本文应用分形理论描述齿轮轮廓,计算和分析不同分形维数D下的时变啮合刚度,研究考虑齿面分形特性的齿轮啮合刚度对齿轮-轴承系统动力学特性的影响.旨在通过研究,探明齿侧间隙和时变刚度等因素对齿轮啮合的动力学特性的影响,为精确建模、齿轮设计和制造提供参考依据.
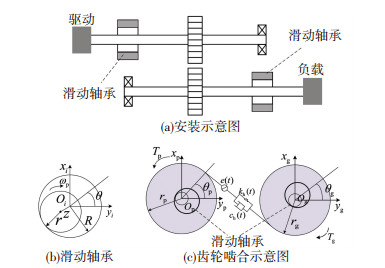
1 系统模型 1.1 齿轮-轴承系统采用考虑齿侧间隙的齿轮-轴承系统模型[12]如图 1所示,模型中齿轮为渐开线直齿轮,轴承为滑动轴承.考虑时变啮合刚度、综合传递误差、齿侧间隙以及滑动轴承非线性油膜力等因素,并考虑轴的径向振动以及两齿轮的扭转振动,但不考虑齿面摩擦力的影响,建立坐标系xiOiyi (i=1或2,表示主、从动轮),其中O1、O2为两轴承几何中心;Op、Og为主从动齿轮几何中心.
|
图 1 齿轮轴承系统 Fig. 1 Gear bearing system |
系统的无量纲动力学方程采用文献[12]中的式(6);kh(t)为时变啮合刚度,综合传递误差e(t)=ecos(ωht);齿轮副间隙非线性函数
| $ {\bar f_{\rm{b}}} = \left\{ {\begin{array}{*{20}{c}} {{{\bar x}_{\rm{h}}} - {{\bar b}_{\rm{h}}}, }&{{{\bar x}_{\rm{h}}} > {{\bar b}_{\rm{h}}};}\\ {0, }&{\left| {{{\bar x}_{\rm{h}}}} \right| \le {{\bar b}_{\rm{h}}};}\\ {{{\bar x}_{\rm{h}}} + {{\bar b}_{\rm{h}}}, }&{{{\bar x}_{\rm{h}}} < - {{\bar b}_{\rm{h}}}.} \end{array}} \right. $ |
模型中,应用Capone[13]修正模型计算滑动轴承的非线性油膜力,滑动轴承的油膜力分布一般由雷诺方程确定,无量纲的油膜力分量如文献[12]中的式(3)所示.
1.2 考虑齿面分形特性的齿轮啮合刚度微观上,齿轮的表面因呈现出随机性、多尺度性和自仿射性,具有分形的基本特征,因此可采用分形理论来描述齿轮表面[12, 14-15].
以渐开线直齿圆柱齿轮为具体对象,建立齿轮齿廓方程[10]:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_i} = {r_i}\cos {\gamma _i}, }\\ {{y_i} = {r_i}\sin {\gamma _i}.} \end{array}} \right. $ | (1) |
式中:γi=s/(2r)-(inv αi-inv α0);s为分度圆齿厚;r为分度圆半径;ri为渐开线齿廓上任一点的回转半径;α0为分度圆压力角,按常用习惯取α0=20°;αi为渐开线齿廓上任一点对应的压力角.使用W-M模型[16]描述齿轮表面的形貌:
| $z(x) = L{\left( {\frac{G}{L}} \right)^{D - 1}}\sum\limits_{n = 0}^\infty {\frac{{\cos \left[ {\left( {2\pi {\gamma ^n}x} \right)/L} \right]}}{{{\gamma ^{(2 - D)n}}}}} . $ | (2) |
式中:z(x)为齿轮形貌高度, x为轮廓的位置坐标, D为分形维数, G为特征尺度系数, γn齿轮轮廓的空间频率, L为取样长度.
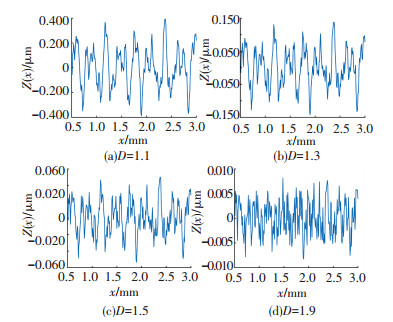
综上,根据式(1)和式(2)可得具有分形特性的齿轮齿廓形貌高度(图 2)和考虑齿面分形特性的齿轮齿廓的渐开线方程,如式(3)所示.从图 2中可以看出,随着分形维数的增加,齿轮形貌高度的幅值变小,并且表现出齿轮粗糙齿面中更多的细节.同时由于齿面形貌的变化,在齿轮啮合的过程中使得轮齿变形量发生变化,进而导致接触刚度发生变化.
| $ \left\{ {\begin{array}{*{20}{l}} {{x_i} = {r_i}\cos {\gamma _i}, }\\ {{y_i} = {r_i}\sin {\gamma _i} + z\left( {{x_i}} \right).} \end{array}} \right. $ | (3) |
|
图 2 具有分形特性的齿轮齿廓形貌高度 Fig. 2 Profile height of gear profile with fractal characteristics |
根据式(3),可得考虑齿面分形特性的粗糙齿面轮廓线,为了更加明显地表现考虑齿面分形特性的齿廓,对其形貌高度进行放大处理,得到如图 3所示的与光滑齿面轮廓线对比示意图.

|
图 3 具有分形特性的齿面轮廓和光滑轮廓示意图 Fig. 3 Sketch of tooth profile and smooth contour with fractal characteristics |
采用Weber-Banaschek方法[17],考虑轮齿的弯曲、剪切变形δZ,轮齿基础部分的变形δR和齿轮的接触变形δpW,计算齿轮的啮合刚度.
| $ \begin{array}{*{20}{c}} {{\delta _{\rm{Z}}} = \frac{{{F_{\rm{N}}}}}{{Eb}}{{\cos }^2}{\alpha _x}\left\{ {10.92\int_0^{{h_x}} {\frac{{{{\left( {{h_x} - y} \right)}^2}}}{{{{(2x)}^3}}}} {\rm{d}}y + } \right.}\\ {3.1\left( {1 + 0.294{{\tan }^2}{\alpha _x}} \right)\int_0^{{h_x}} {\frac{{{\rm{d}}y}}{{2x}}} \} , }\\ {{\delta _{\rm{R}}} = \frac{{{F_{\rm{N}}}}}{{Eb}}{{\cos }^2}{\alpha _x}\left\{ {5.2\frac{{h_x^2}}{{S_{\rm{F}}^2}} + \frac{{{h_x}}}{{{S_{\rm{F}}}}} + 1.4\left( {1 + 0.294{{\tan }^2}{\alpha _x}} \right)} \right\}.} \end{array} $ |
式中:x、y分别为轮齿啮合法向力作用点处的坐标,αx为作用点的啮合角,FN为接触点压力,E为综合弹性模量,b为齿宽.
接触产生的变形量如式(4)所示,a为赫兹接触半径,其表达式如式(5)所示,进而得到齿轮的啮合刚度k,如式(6)所示.
| $ {\delta _{{\rm{pW}}}} = 0.58\frac{{{F_{\rm{N}}}}}{{Eb}}\left( {{\mathop{\rm In}\nolimits} \frac{{2{h_1}}}{a} + {\mathop{\rm In}\nolimits} \frac{{2{h_2}}}{a} - 0.429} \right), $ | (4) |
| $ a = 1.52\sqrt {\frac{{{F_{\rm{N}}}}}{{Eb}}} \sqrt {\frac{{{\rho _1}{\rho _2}}}{{{\rho _1} + {\rho _2}}}} , $ | (5) |
| $ \begin{array}{*{20}{c}} {{\delta _\Sigma } = {\delta _{{\rm{Z}}1}} + {\delta _{{\rm{Z}}2}} + {\delta _{{\rm{R}}1}} + {\delta _{{\rm{R}}2}} + {\delta _{{\rm{pW}}}}, }\\ {k = {F_{\rm{N}}}/{\delta _\Sigma }.} \end{array} $ | (6) |
式中,ρ1和ρ2分别为两个齿轮轮齿的齿面在接触点处的曲率半径,其他具体参数如图 4所示.

|
图 4 Weber-Banaschek公式中的轮齿几何参数 Fig. 4 Geometric parameters of the tooth in the formula of Weber-Banaschek |
由式(6)可知,刚度是轮廓位置坐标的函数,将随其变化而发生变化,又由于齿轮转速将轮廓位置坐标和时间相关联,故,刚度将随时间变化而变化,具有时变特性.
综上,得到不考虑齿面分形特性和不同分形维数D下的齿轮啮合刚度,如图 5所示.从图 5中可以看出,随着分形维数的增加,齿轮的时变啮合刚度的整体趋势相同,但是在考虑分形理论之后,齿轮轮廓的形貌高度随轮廓的位置发生变化,啮合刚度随之产生波动,并且随着分形维数D的增加,齿轮表面越来越精细,形貌高度变小,刚度波动减小,趋向图 5(a)中所示正常刚度.另外,不同分形维数D下的刚度的平均值如表 1所示,随着D的减小,齿轮齿面粗糙度增大,啮合刚度降低,与文献[18]中结论相似.

|
图 5 时变啮合刚度 Fig. 5 Time-varying meshing stiffness |
| 表 1 齿轮啮合刚度平均值 Tab. 1 Mean value of gear meshing stiffness |
将时变啮合刚度模型代入考虑齿面分形特性的齿轮系统,采用4-5阶Runge-Kutta方法进行仿真分析,可得到系统的分岔图、三维频谱图、时域图以及均方根图等.为了验证其仿真结果的准确性,由于目前国内外公开发表的文献中未能找到与其相关的可参考信息,后续将采用利用齿轮的振动位移等效啮合点位移的方法进行实验分析验证.
2.1 分形维数D对系统响应的影响为了研究分形维数D对系统响应的影响,取系统参数ki=1.2,bh=0.2 mm,ep=eg=0.01,e=0.1,ζh=0.01,ζ1=ζ2=ζp=ζg=0.01,Fm=0.105,Fa=0,D=1.5,关于齿轮-轴承系统的其他结构参数如表 2所示,仿真结果如图 6所示.
| 表 2 系统结构参数值 Tab. 2 Parameter values of the system |
|
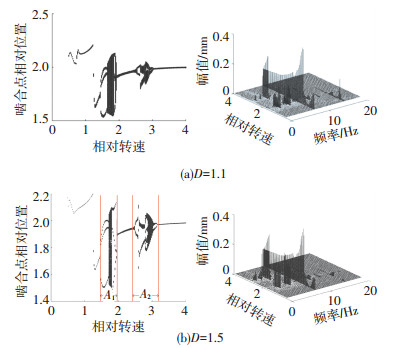
图 6 系统分岔图和三维频谱图 Fig. 6 System bifurcation diagram and three-dimensional spectrum diagram |
由图 6(b)中可以看出,当ω < 1.5时,系统处于单周期或双周期运动,系统的运动状态比较稳定;当1.5 < ω < 2.1时,系统进入运动区域A1,单周期分岔为三周期,之后进入混沌,持续一段时间后又变为三周期运动,最后回归稳定的单周期运动,随之进入运动区域A2;当ω > 2.4时,先后经历两周期、拟周期、四周期、两周期、拟周期和混沌等运动,最终回归单周期运动.从图 6(b)的三维频谱中,可以看出,在相对低速区域A1,系统的频率成分主要集中在1/3fm,2/3fm,fm和2fm次谐响应;在相对高速区域A2,系统的频率成分主要集中在1/2fm和fm次谐响应.
从图 6可以看出,当D=1.1时,由于刚度的波动加剧,系统振动的相对位移稍变大,运动区域A1和A2中的周期运动变为拟周期运动,并且进入混沌区域的时间点提前,混沌和拟周期运动区域增大,系统的不稳定性增大.
为了研究单一转速下,刚度对系统响应的影响情况,令ω=1.7,ki=1.6,其余参数保持不变.为了凸显分形维数D的变化对系统的影响,更明显地进行对比分析,只列举D分别取1.1、1.5和1.9时,系统的相图和Poincaré截面图,如图 7所示;D分别取1.1、1.3、1.5和1.9时,系统的时域图及幅值均方根图如图 8和图 9所示.

|
图 7 系统相图和Poincaré截面图 Fig. 7 System phase diagram and Poincaré section |

|
图 8 系统时域图 Fig. 8 Time domain diagram of the system |
|
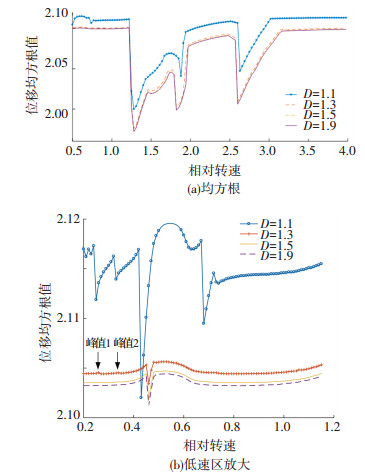
图 9 不同分形维数下的系统均方根 Fig. 9 Root mean square of the system under different fractal dimensions |
从图 7中可以看出,随着D的减小,齿轮系统从标准的三周期运动向拟周期运动过渡,Poincaré截面图中由最开始的3点到后来的3簇,逐渐扩散,系统趋向于不稳定的拟周期运动.
从图 8中可以看出,随着分形维数D的增大,系统振幅变化的整体趋势基本相同,其中D=1.1和D=1.3的幅值波动情况更为明显,结合表 3所示的振动位移均方根值可以发现,虽然D=1.5和D=1.9时的时域图变化不大,但D=1.5时的均方根值稍大,也就是说,随着D的减小,齿面更加精细,系统振动位移减小,系统运动相对更加稳定.
| 表 3 ω =1.7时不同分形维数下的均方根值 Tab. 3 Root mean square values under different fractal dimensions when ω=1.7 |
从图 9(a)中可以看出,当D=1.1和D=1.3时的均方根值变化幅度较大,D=1.5和D=1.9时变化幅度变小,这和图 5刚度的变化情况相对应;图 9(b)为低速时均方根值的放大图,从图中可以看出,当D=1.1时,在低速区出现多个峰值,系统相对不稳定,随着D的增大,系统均方根曲线变得平稳,在ω=0.3附近出现了峰值1、2,在ω=0.5附近也出现了峰值,与文献[19]中情况类似,符合齿轮的运动规律.
2.2 含随机扰动的时变刚度对系统响应的影响为了验证本文提出的考虑齿面分形特性的时变刚度模型对系统响应分析的敏感性和优点,与含服从正态分布的随机扰动分量的时变啮合刚度模型进行对比.含随机扰动分量的刚度模型表达式为[8]
| $ {k_{\rm{h}}} = 1 - \left( {{\varepsilon _{\rm{r}}} + {\omega _\Delta }} \right)\cos \left( {{\mathit{\Omega} _{\rm{h}}}\tau } \right). $ | (7) |
式中:εr为量纲一齿轮啮合刚度、ω△为服从高斯分布的量纲一啮合刚度的随机扰动量,Ωh=ωh/ωn.
将由式(6)得到的不同分形维数下的刚度值与正常刚度值的差值作为刚度波动数组,该数组的均值和方差如表 4所示,代入式(7),得到含随机扰动的时变啮合刚度,进而进行系统响应的分析,相关结果如图 10和图 11所示.
| 表 4 不同扰动的时变刚度下均方根值 Tab. 4 Root mean square values under time varying stiffness under different disturbances |
|
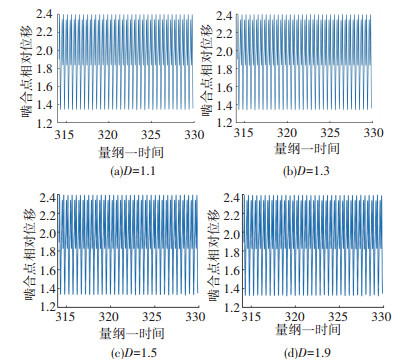
图 10 系统时域图 Fig. 10 Time domain diagram of the system |
|
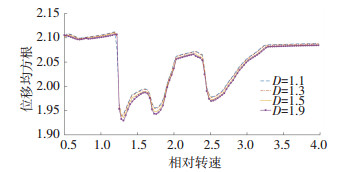
图 11 不同随机扰动下的系统均方根图 Fig. 11 Root mean square of the system under different random disturbances |
从图 10中的时域图可以看出,系统在不同随机扰动下的位移变化差别不大,但从表 4和图 11中看出,随着均值和方差的变化,系统振动的位移减小;与上节进行对比可知,随着分形维数D的减小,刚度波动降低,计算得到的方差变小,在服从正态分布的随机扰动下的系统振动位移减小,系统趋于稳定,但系统对于考虑齿面分形特性的时变啮合刚度的变化更加敏感,体现出由于齿面变化导致系统响应变化中的更多细节.
2.3 阻尼比对系统响应的影响为了研究阻尼比对齿轮-轴承系统动力学特性的影响,取参数D=1.5,ki=1.2,阻尼比ζ分别为0.01、0.05和0.10,结果如图 12所示.
|
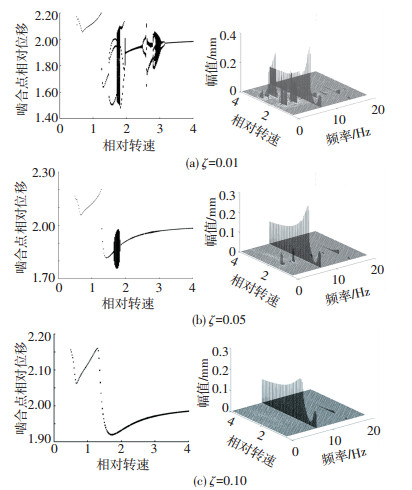
图 12 不同阻尼比下的系统分岔图和三维频谱图 Fig. 12 System bifurcation diagram and three-dimensional spectrum map under different damping ratios |
从图 12可以看出,在ζ=0.01时,对于ω < 1.2区域,系统一直保持着单周期运动,之后存在两个不稳定区域;随着ζ的增大,当ζ=0.05时,两个不稳定区域均趋于稳定,低速区域由周期运动与混沌运动的混合区域转换为较小区域的拟周期及混沌运动,高速区域整体收缩;当ζ=0.1时,系统混沌区域消失,变为单周期运动.
3 结论1) 在考虑齿面分形特性的齿轮-轴承系统中,随着分形维数D的增大,齿轮轮齿表面更加精细,时变啮合刚度的波动降低,系统趋于相对稳定的周期运动.
2) 齿轮-轴承系统对于考虑齿面分形特性的时变啮合刚度的变化更加敏感,由分形维数D的变化导致的齿轮齿廓的变化对系统响应有较大的影响.
3) 随着阻尼比的增大,系统趋向稳定,当阻尼比增大到一定程度时,系统会变为单周期稳定运动.
| [1] |
LING Xiang, YI Jia, HU Aijun. Bifurcation and chaos analysis for multi-freedom gear-bearing system with time-varying stiffness[J]. Applied Mathematical Modelling, 2016, 40(23/24): 10506. DOI:10.1016/j.apm.2016.07.016 |
| [2] |
赵韩, 吴其林, 黄康, 等. 国内齿轮研究现状及问题研究[J]. 机械工程学报, 2013, 49(19): 11. ZHAO Han, WU Qilin, HUANG Kang, et al. Status and problem research on gear study[J]. Journal of Mechanical Engineering, 2013, 49(19): 11. |
| [3] |
KAHRAMAN A, SINGH R. Non-linear dynamics of a spur gear pair[J]. Journal of Sound & Vibration, 1990, 142(1): 49. DOI:10.1016/0022-460X(90)90582-K |
| [4] |
KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system[J]. Journal of Sound & Vibration, 1991, 146(1): 135. |
| [5] |
CHEN Siyu, TANG Jinyuan, LUO Caiwang, et al. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction[J]. Mechanism & Machine Theory, 2011, 46(4): 466. DOI:10.1016/j.mechmachtheory.2010.11.016 |
| [6] |
WU Shijing, ZHANG Haibo, WANG Xiaosun, et al. Influence of the backlash generated by tooth accumulated wear on dynamic behavior of compound planetary gear set[J]. Journal of Mechanical Engineering Science, 2016, 231(11). DOI:10.1177/0954406215627831 |
| [7] |
魏莎, 韩勤锴, 褚福磊. 考虑不确定性因素的齿轮系统动力学研究综述[J]. 机械工程学报, 2016, 52(1): 1. WEI Sha, HAN Qinkai, CHU Fulei. Review on research of uncertain dynamics for gear system[J]. Journal of Mechanical Engineering, 2016, 52(1): 1. |
| [8] |
王靖岳, 郭立新, 张亮, 等. 齿轮传动系统随机振动模型与仿真[J]. 东北大学学报(自然科学版), 2013, 34(4): 578. WANG Jingyue, GUO Lixin, ZHANG Liang, et al. Stochastic vibration model and simulation of gear transmission system[J]. Journal of Northeastern University (Natural Science), 2013, 34(4): 578. DOI:10.12068/j.issn.1005-3026.2013.04.029 |
| [9] |
廖映华, 秦大同, 刘长钊. 考虑内部激励随机性的两级分流式人字齿轮传动动力学特性[J]. 振动与冲击, 2015(1): 206. LIAO Yinghua, QIN Datong, LIU Changzhao. Dynamic characteristics of two-stage split herringbone gear trains considering the randomness of internal excitations[J]. Journal of Vibration and Shock, 2015(1): 206. |
| [10] |
冯松, 毛军红, 谢友柏. 齿面磨损对齿轮啮合刚度影响的计算与分析[J]. 机械工程学报, 2015, 51(15): 27. FENG Song, MAO Junhong, XIE Youbai. Analysis and calculation of gear mesh stiffness with tooth wear[J]. Journal of Mechanical Engineering, 2015, 51(15): 27. |
| [11] |
陈奇, 黄守武, 张振, 等. 考虑摩擦因素的两圆柱体表面接触承载能力的分形模型研究[J]. 机械工程学报, 2016, 52(7): 114. CHEN Qi, HUANG Shouwu, ZHANG Zhen, et al. Research on fractal contact model for contact carrying capacity of two cylinders' surfaces considering friction factors[J]. Journal of Mechanical Engineering, 2016, 52(7): 114. |
| [12] |
李小彭, 牟佳信, 潘五九, 等. 具有分形特性的齿侧间隙对齿轮-轴承系统动态特性的影响[J]. 机械工程学报, 2018, 54(9): 153. LI Xiaopeng, MU Jiaxin, PAN Wujiu, et al. Influence of fractal backlash on dynamic behavior of gear-bearing system[J]. Journal of Mechanical Engineering, 2018, 54(9): 153. |
| [13] |
CAPONE G, RUSSO M, RUSSO R. Dynamic characteristics and stability of a journal bearing in a non-laminar lubrication regime[J]. Tribology International, 1987, 20(5): 255. DOI:10.1016/0301-679X(87)90025-9 |
| [14] |
PAN Wujiu, LI Xiaopeng, WANG Linlin, et al. Influence of contact stiffness of joint surfaces on oscillation system based on the fractal theory[J]. Archive of Applied Mechanics, 2017, 1. |
| [15] |
李小彭, 潘五九, 高建卓, 等. 结合面形貌特性对模态耦合不稳定系统的影响[J]. 机械工程学报, 2017, 53(5): 116. LI Xiaopeng, PAN Wujiu, GAO Jianzhuo, et al. Influence of surface topography characteristics on mode coupling instability system[J]. Journal of Mechanical Engineering, 2017, 53(5): 116. |
| [16] |
冯兰兰, 汪久根. 齿轮齿面的分形模拟[J]. 机械传动, 2014(2): 50. FENG Lanlan, WANG Jiugen. Fractal simulation of gear tooth surface[J]. Journal of Mechanical Transmission, 2014(2): 50. |
| [17] |
王晓笋, 巫世晶, 周旭辉, 等. 含磨损故障的齿轮传动系统非线性动力学特性[J]. 振动与冲击, 2013, 32(16): 39. WANG Xiaosun, WU Shijing, ZHOU Xuhui, et al. Nonlinear dynamics analysis of gear transmission system with wear fault[J]. Journal of Vibration & Shock, 2013, 32(16): 39. DOI:10.3969/j.issn.1000-3835.2013.16.007 |
| [18] |
赵韩, 陈奇, 黄康. 两圆柱体结合面的法向接触刚度分形模型[J]. 机械工程学报, 2011, 47(7): 54. ZHAO Han, CHEN Qi, HUANG Kang. Fractal model of normal contact stiffness between two cylinders'joint interfaces[J]. Journal of Mechanical Engineering, 2011, 47(7): 54. |
| [19] |
陈思雨, 唐进元. 间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响[J]. 机械工程学报, 2009, 45(8): 119. CHEN Siyu, TANG Jinyuan. Effect of backlash on dynamics of spur gear pair system with friction and time-varying stiffness[J]. Journal of Mechanical Engineering, 2009, 45(8): 119. |
 2019, Vol. 51
2019, Vol. 51


