故障诊断作为设备基于状态维护(Condition-based Maintenance, CBM)的关键之一[1],受到学者和工业界的广泛关注.而深度学习方法由于深度结构具备高度的非线性抽象和拟合功能,不仅在机器视觉和自然语言处理等领域取得重大的突破[2],其中很多模型如卷积神经网络、深度信念网(deep brief network, DBN)和堆叠自编码器(stacked autoencoder, SAE)等也在机械设备故障诊断中得到广泛地应用.文献[3]提出一种基于堆叠自编码器的旋转机械故障诊断模型,模型由3个自编码器堆叠而成并利用频谱特征进行训练和诊断.文献[4]提出一种基于DBN的多传感器故障诊断模型,并利用benchmark分类数据集进行验证.上述成果虽然在故障诊断上取得较好的准确度,但其输入特征仍需人工提取,由于依赖专家知识和不同问题的差异性,采用人工特征提取不仅耗时而且推广性差.而卷积神经网络由于(convolution neural network, CNN)独特的卷积结构所带来强大的特征提取能力,是解决这一问题的理想模型.
卷积神经网络在手写字体识别上取得成功[5],即LeNet-5.其后,AlexNet[6]、GoogleNet[7]和ResNet[8]等结构更深、处理能力更强的模型在图像识别领域取得重大突破.除了在图像识别领域取得成功,CNN在故障诊断领域也有广泛的应用.文献[9]提出一种基于LeNet-5的故障诊断模型,并将原始时域信号转换成二维灰度图像作为模型输入,实现轴承和离心泵的故障诊断.文献[10]提出基于浅层卷积神经网络的模型,结合原始信号离散傅里叶变换得到的特征进行诊断.除了将CNN诊断模型作用于人工提取的信号特征,一些学者提出直接作用于原始时域信号的诊断模型.文献[11]提出一种改进一维卷积核的卷积神经网络模型,利用原始的电流信号实现电机实时故障诊断,但其诊断精度仅为97.4%.文献[12]采用包含单卷积层和两层全连接层的CNN模型,并利用原始振动信号实现齿轮箱的故障诊断.文献[13]提出一种基于深度一维卷积神经网络的故障诊断模型,并利用较大尺寸的卷积核,小批量训练和卷积核dropout和,实现基于原始振动信号准确和稳定的诊断,同时模型具备较好的抗噪性能.
虽然上述深度学习故障诊断模型已达到较好的诊断效果,甚至有些模型的诊断精度已经接近100%[9][13],但是仍然存在以下问题:1)当前深度学习模型由于深度结构和全连接层的存在,训练和诊断的计算量均比较大,导致模型很难应用于实时性要求很高的场景;2)当前提出的模型绝大多数未考虑到信号混有噪声情况下的诊断,而实际生产的复杂性难免会导致信号噪声,这将大大降低模型诊断的准确性和稳定性.
针对上述问题,本文提出一种基于一维卷积神经网络的抗噪故障诊断模型(1-D convolutional neural network diagnosis model with anti-noise, ACNNDM-1D),模型采用一维卷积核和池化核以直接作用于原始时域信号,实现特征提取和状态分类.和已有模型相比,本文针对模型计算量大和抗噪能力差的问题作两点改进:1)利用全局平均池化层代替传统卷积神经网络中的全连接层,在降低计算量的同时,也降低模型的参数量和过拟合的风险;2)模型利用随机破坏的原始信号进行训练,以提高训练后模型的抗噪诊断能力.并利用轴承和齿轮箱的数据集对改进后模型实时及抗噪诊断的有效性进行验证.
1 卷积神经网络和LeNet-5 1.1 卷积神经网络CNN是一种特殊结构的前馈神经网络,一般包含卷积层、池化层和全连接层.其中卷积层和池化层实现特征提取,全连接层利用提取的特征实现分类或者回归.
1.1.1 卷积层运算卷积层利用多卷积核(convolutional kernel)对输入数据进行卷积处理并输出卷积后的特征,即特征图(feature map).每一个卷积核输出一个特征图,对应提取到的一类特征.由于同一卷积核卷积操作中的局部连接、参数共享和多卷积核特性,相比于全连接层,卷积层在参数较少的情况下能提取更丰富的特征.由于不受输入维度的影响且很容易训练深度结构,卷积结构是复杂高维输入特征提取的有效工具.卷积操作的公式为
| $ g(i) = \sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {\sum\limits_{z = 1}^p {{a_{x, y, z}}} } } \times w_{x, y, z}^i + {b^i}, i = 1, 2, \ldots , q. $ |
式中:i为第i个卷积核;g(i)为第i个卷积核学习得到的特征图;a为输入数据;b为卷积核的偏置;x、y、z为输入数据的维度,对于一维时域信号,只需对后两个维度进行简化即可.
在完成卷积操作后,通常利用激活函数实现非线性变换,其中ReLU激活函数在CNN中应用最为广泛,其运算式为
| $ y(i) = f(g(i)) = \max \{ 0, g(i)\} , i = 1, 2, \ldots , q. $ |
池化层通过池化核对输入特征向量进行降采样(down sampling),在实现数据降维的同时进一步突出提取的特征.池化包括最大池化和平均池化:
| $ \begin{array}{l} p_{{\max}}^{l(i, j)} = \mathop {\max }\limits_{(j - 1)w < t < jw} \left\{ {{a^{l(i, t)}}} \right\}, j = 1, 2, \ldots , q, \\ p_{{\rm{avg}}}^{l(i, j)} = \mathop {{\mathop{\rm avg}\nolimits} }\limits_{(j - 1)w < t < jw} \left\{ {{a^{l(i, t)}}} \right\}, j = 1, 2, \ldots , q. \end{array} $ |
式中:al(i, t)为第l层中,第i个特征图的第t个神经元. w为卷积核的宽度,j为第j个池化核.
1.2 LeNet-5及其应用现状LeNet-5是由LeCun在1998年提出的经典卷积神经网络[5],包括两层卷积层、两层池化层和三层全连接层.虽然LeNet-5最早应用于二维图像,通过将一维时域信号转换成二维图像或者模型采用一维卷积结构,LeNet-5已经成功应用于机械设备故障诊断.但是受经典结构的影响,当前提出的模型均采用2~3层全连接层[11~15],虽然全连接层能实现有效的分类,但是也带来两个问题:首先是全连接层大量的连接将导致巨大的计算开销,使模型难以满足实时性要求较高的场景;其次全连接层大量的参数(占LeNet-5和AlexNet等卷积神经网络90%以上)将带来过拟合的风险.在近几年提出的GoogleNet、MobileNet和ShuffleNet等模型中,全连接层均采用全局平均池化代替以降低模型的连接数和参数量,取得了较好的效果,但这种改进在机械故障诊断领域尚未得到研究和验证.此外,当前提出的绝大多数模型未考虑噪声环境下的诊断问题,而在复杂的工业生产中噪声在所难免,混入噪声的信号将使模型诊断的准确率和稳定性大大降低.
2 ACNNDM-1D故障诊断模型提出基于一维卷积神经网络的抗噪故障诊断模型ACNNDM-1D,针对计算量和抗噪问题作如下改进:
1) 为了降低计算量和过拟合的风险,模型采用全局平均池化层代替全连接层以实现故障分类.相比全连接层,全局平局池化连接数和参数数量远小于前者,因此理论上其应用将对模型计算量大和过拟合问题起到改善作用.
2) 为了提高模型的抗噪能力,模型采用随机破坏的原始信号进行训练,这里所谓的随机破坏,是指对输入样本的数据点按一定的比例随机选取并置零,即神经网络模型中常用的dropout,破坏的比例即为破坏率.文献[14]指出,训练样本随机置零可以给输入信号制造噪声,使训练后的模型即使在训练集和测试集有不同分布的情况下也有较好的效果.
除此之外,模型采用一维卷积和池化结构,直接作用于原始时域信号并实现自适应特征提取和故障分类.
2.1 ACNNDM-1D结构ACNNDM-1D结构和参数如图 1所示.

|
图 1 ACNNDM-1D结构 Fig. 1 Architecture of ACNNDM-1D |
模型包含两层卷积层、一层最大池化层和一层全局平均池化层.模型的输入维度等于样本信号维度,输出维度模型的分类类别,即诊断对象的健康状态数. 图 1中各层参数解释如下:50-S20-16表示卷积核的宽度为50,步长为20,共有16个卷积核;3-S2表示池化核宽度为3,步长为2;最后一层卷积层中的H代表其卷积核数等于模型输出类别数H,其随后的全局平均池化层将输出的H个特征图池化为维度为H的输出.
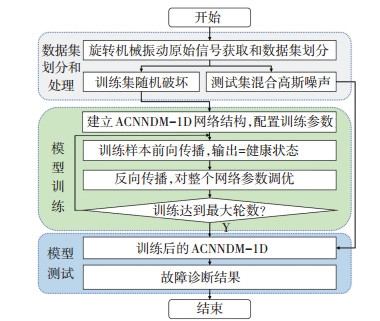
2.2 ACNNDM-1D模型构建ACNNDM-1D模型的构建可以划分为如图 2所示的3个阶段:1)数据集划分和预处理;2)模型训练;3)模型测试.训练集和测试集按比例划分,并将训练集中的样本按一定比例随机破坏(置零),同时为了测试训练后模型的抗噪能力,在测试集中混入高斯白噪声以模拟噪声环境下采集的数据.
|
图 2 ACNNDM-1D构建流程图 Fig. 2 Flowchart of ACNNDM-1D construction |
模型训练的超参数设置如下:网络权重矩阵和偏置初始值通过Xavier函数[15]初始化,学习率利用指数衰减设置,初始学习率和衰减率分别为0.035和0.990,截止训练轮数设置为5 000,每轮训练输入的样本数为100.模型训练在达到截止训练轮数后停止,并利用含噪声的测试集进行多次测试,以平均诊断精度和标准差作为测试结果.模型训练和测试的硬件环境为Intel i7-5820k + NVidia 1080ti,软件环境为Windows10 + Python3.5 + TensorFlow.
3 旋转机械故障诊断实验旋转机械故障诊断实验对象为轴承和齿轮箱,实验台如图 3所示,从左至右分别为电机、齿轮箱、3个轴承和磁粉制动器,其中齿轮箱为二级齿轮箱,轴承均为同型号单列滚子轴承(N205E),轴承2处可以通过螺旋机构给3个轴承施加径向载荷,磁粉制动器可施加轴向载荷.轴承的节圆直径为38.5 mm,滚子直径为6.5 mm,滚子数为13;齿轮箱齿轮模数为2 mm,齿宽为20 mm,压力角为20°,齿轮间隙为0.5 mm,主动和从动齿轮齿数分别为55和75.

|
图 3 旋转机械故障诊断实验台 Fig. 3 Fault diagnosis test rig of rotating machinery |
故障诊断实验对象为轴承3,实验过程中,径向负载和轴向负载均设为0,电机的转速设为1500 r/min.振动数据通过数据采集器(UT3408FRS-ICP)和安装在轴承座竖直径向上的传感器(YD-186)获取,采集频率设为20.480 kHz.轴承共包含4种状态:正常、内圈故障、外圈故障和滚子故障.其中每一种故障状态各包含宽度为0.18、0.36、0.54 mm的3种故障程度,因此共包含10种故障状态.故障通过切割方式加工,深度均为0.1 mm,呈沟槽状.对应10种故障状态,共进行10组实验,每次实验进行20 min,结束后更换相应的故障轴承.
对应10种轴承状态,每种状态取2 000个样本,故样本集共含200 000个样本.每个样本包含2 000个数据点,相应的ACNNDM-1D输入维度为2 000,输出维度为10.样本集利用分层采用的方法进行划分,9/10的样本用于训练,其余的用于测试.
对于每一个训练样本,采用不同程度的破坏处理,破坏率在0~0.8范围内随机取值.对于测试样本,通过在原始样本中加入高斯白噪声来模拟噪声环境下的故障诊断.考虑到模型在训练时无法获知关于噪声的信息,这样的训练和测试方法也比较符合实际工业应用场景.样本中的噪声含量通过信噪比来衡量:
| $ {R_{{\rm{SN}}}} = 10\lg \left( {\frac{{{p_{{\rm{ signal }}}}}}{{{p_{{\rm{ noise }}}}}}} \right). $ |
式中:psignal为信号的有效功率,pnoise为噪声的有效功率.
为了测试不同噪声含量下训练后模型的诊断效果,通过在测试集中添加不同含量的噪声形成多个测试集并分别测试,测试集信噪比取值为-2~12 dB的整数,因此共包含15个测试集.
3.1.1 输入破坏训练验证模型训练结束后,利用含噪测试集对模型的诊断精度进行测试.首先为了验证随机破坏输入策略对训练后模型抗噪能力的影响,对比采用该策略和使用干净信号训练的模型在不同SNR的测试集下的诊断精度,为了保证实验结果的可靠性,两者各进行5次实验,并计算5次实验结果的均值和标准差,实验结果见表 1.
| 表 1 有、无破坏输入训练模型的诊断精度 Tab. 1 Diagnosis accuracy of dropout and non-dropout input training models |
从诊断结果可以看出,采用随机破坏输入策略训练的模型即使是在信噪比为-2 dB的情况下仍能达到91.79%±0.11%的诊断精度,而后者仅为45.20%±3.92%,在信噪比<6 dB的情况下,前者的诊断精度和稳定性均远优于后者.可见,采用常规干净信号训练模型的抗噪能力较差,而采用随机破坏输入训练策略对模型在噪声环境下的诊断准确性和稳定性均有较大的改善作用,大大提高了模型的抗噪能力.
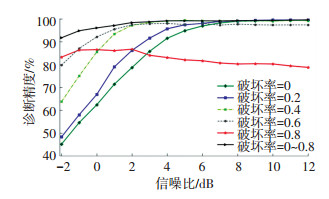
3.1.2 输入样本破坏率选择输入样本的随机破坏率的选取是影响训练后模型的诊断精度关键因素之一. 图 4为不同破坏率输入训练的模型诊断精度,从实验结果可知,在训练样本破坏率保持不变的条件下,破坏率越大,训练后模型在信噪比<4 dB的测试集中诊断精度越高.但是,当破坏率高于0.6时,训练后的模型在信噪比>5 dB的测试集中诊断精度明显下降,在破坏率为0.8时尤为明显.由此可见,提高输入样本的破坏率虽然有助于提高模型的抗噪能力,但是会降低高信噪比测试集的诊断精度.为了解决这一矛盾,本文对每一个训练样本应用0~0.8随机变化取值的破坏率,样本集中高破坏率样本保证训练后模型在低信噪比下测试集的诊断精度,低破坏率样本保证模型在高信噪比测试集上的诊断精度,从图 4可以看出,采用变化破坏率训练的模型在所有测试集上均取得较高的诊断精度,并优于采用固定破坏率训练的模型.
|
图 4 不同输入破坏率训练的模型诊断精度 Fig. 4 Diagnosis accuracy of models trained by input with different dropout rates |
为了验证模型采用全局平均池化作为分类层对诊断精度和计算量的影响,作为对比模型,将ACNNDM-1D的全局池化层替换成一般的全连接层,由于当前模型一般采用3层全连接层的结构[11, 13, 16], 对比模型的全连接层的结构也采用3层的结构,其维度分别为200、100和10.除全连接层外,模型的其他结构和参数保持相同,并且采用相同的破坏输入训练集和相同的测试集.
1) 诊断结果对比.对比实验同样进行5次,取均值作为实验结果,如图 5所示.由于采用全局平均池化和全连接层的模型在训练集上的诊断精度均为100%,而测试集诊断精度均不足100%,故两者均出现一定程度的过拟合,但是诊断精度上全局平均池化模型要高于全连接层模型,并且在信噪比<7 dB条件下差距尤为明显.可见,由于采用平均池化的模型参数量少,所以其过拟合程度轻;而对于信噪比越低的测试集,出现过拟合的可能性越高,这也解释了为什么采用全局平均池化的模型相比采用全连接层的模型,在信噪比较低的测试集诊断中优势较为明显.

|
图 5 采用全局平均池化和全连接模型诊断精度对比 Fig. 5 Diagnosis accuracy comparison of models with global average pooling and fully connected layers |
2) 计算量对比.为了比较两者在计算量上的差别,分别对两者在相同训练集下进行10组训练(5 000×100样本)和1 000组测试(2 000样本).考虑到嵌入式设备低算力情况,实验采用i5-4210u(主频1.7 GHz)硬件平台进行实验.实验结果如表 2所示,可以看出,采用平均池化后模型相比采用全连接层的模型在训练耗时和测试耗时上有12.93%和12.5%的减少,其中采用全局平均池化的ACNNDM-1D模型诊断2 000个样本仅耗时(0.147±0.016)s,可以满足实时性要求较高的工业场景.
| 表 2 采用全连接层和全局平均池化模型训练和测试耗时对比 Tab. 2 Training and testing time comparison of models with fully connected and global average pooling layers |
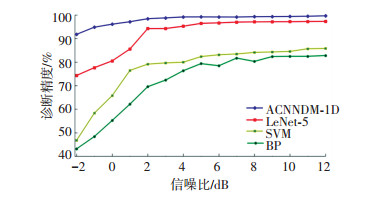
将经典二维LeNet-5、支持向量机(SVM)和BP神经网络和本文提出模型作对比.其中LeNet-5的输入维度为45×45,卷积核、池化核和全连接层均不作改动. SVM模型采用高斯核函数,BP神经网络输入层、隐层和输出层维度分别为2 000、500、10,激活函数为sigmoid函数.模型诊断的对比结果如图 6所示,从图 6可看出,本文提出模型相比经典二维LeNet-5模型,在所有的含噪测试集上诊断精度均有较大的提升,该结果证明改进的一维卷积模型更适合时域信号的处理.同时相比典型的浅层模型SVM和BP神经网络,诊断精度和稳定性上在所有的含噪测试集上均有较大优势,浅层模型即使在含噪较少的测试集上的诊断精度也比较低,其原因在于浅层模型特征学习能力有限,学习到的特征不具备较好的分类特性.
|
图 6 ACNNDM-1D和其他经典模型对比 Fig. 6 Comparison of ACNNDM-1D and other classic models |
齿轮箱故障诊断实验的对象为从动齿轮,实验条件和轴承故障诊断实验保持一致,并在实验过程中保证所有轴承为正常状态.振动信号通过垂直安装在齿轮箱端盖上的传感器采集并且采集频率同样设为20 480 Hz.从动齿轮共包含5种状态:正常、断齿故障、齿轮点蚀、齿轮裂纹和齿轮磨损.除了将模型的输出维度对应于齿轮的5种健康状态设为5之外,其余的参数设置和数据集划分与轴承故障诊断实验相同.
3.2.1 破坏输入训练验证和轴承故障诊断实验一样,利用不同含噪测试集对采用随机破坏输入的模型和采用干净输入训练的模型进行测试和对比,实验结果如表 3所示.采用随机破坏输入策略训练的模型在信噪比<8 dB的测试集中,相比于采用干净输入训练的模型均有较大的优势,并且在信噪比为-2 dB的条件下仍能达到92.71%±1.68%的精度,而后者仅为59.55%±10.44%,可见在齿轮箱故障诊断实验中,采用随机破坏输入训练策略可以显著提升模型在噪声环境下诊断的准确性和稳定性.
| 表 3 有无破坏输入训练模型的诊断精度 Tab. 3 Diagnosis accuracy of dropout and non-dropout input training models |
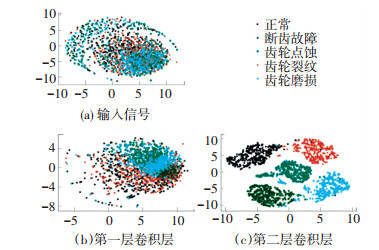
为了验证模型对于原始输入信号的自适应特征学习能力,利用t-SNE(t-distributed stochastic neighbor embedding)方法在信噪比等于0 dB的测试集下对ACNNDM-1D各卷积层学习到的特征进行可视化分析,如图 7所示.
|
图 7 学习特征t-SNE分析 Fig. 7 t-SNE analysis of learned features |
模型的原始输入的可分类性非常差,而随着深度的增加,卷积层提取的特征分离度越来越高,可分类性越来越好,在第二层卷积层提取的特征中,其聚集程度已足以区分齿轮的各种故障状态以获得足够的诊断精度,由此可见,ACNNDM-1D可以从含噪信号中学习有效的特征以实现精确的故障诊断.
3.3 开源轴承数据集验证上述轴承和齿轮箱故障诊断实验是在负载保持不变的情况下进行的,为了验证模型在变负载条件下的有效性,利用凯斯西储大学的开源轴承数据集[17]进行故障诊断实验.用于实验的数据为实验台的电机驱动端轴承振动数据,同样包含正常、内圈故障、外圈故障和滚子故障4种健康状态,每种故障包含宽度为0.07、0.14和0.21 mm的3种故障程度,因此数据集共有10种故障状态.其中每一种故障状态包含4种负载(0、1、2、3 hp)下采集的数据,4种负载对应的转速分别为1 797、1 772、1 750和1 730 r/min,基本可以视为定速,振动数据的采样频率为12 kHz.
对于每一种故障状态,4种负载条件下各取200个样本,同样采用分层采样的方法,9/10的样本用于训练,其余的用于测试,因此训练集包含7 200个样本,测试集包含800个样本.
利用不同信噪比的测试集对采用随机破坏输入训练的模型和采用干净输入训练的模型进行测试和对比,实验结果如表 4所示.
| 表 4 有无破坏输入训练模型的诊断精度 Tab. 4 Diagnosis accuracy of dropout and non-dropout input training models |
由表 4可知,采用随机破坏输入训练的模型在所有测试集上的诊断精度均高于采用干净输入训练的模型,并且在信噪比为-2 dB的条件下达到91.33%的精度,而后者仅为44.97%;同时在信噪比>2 dB时,模型的诊断精度均高于98%;在信噪比>7 dB的条件下,模型的诊断精度高于99%.由此可以说明,在变负载的条件下,本文提出模型同样可以实现噪声环境下准确而稳定的故障诊断,同时随机破坏输入策略能大大提高模型的抗噪能力.
4 结论1) 本文提出模型可以从原始信号中提取有效故障特征,并实现旋转机械在噪声环境和变负载条件下准确而稳定的故障诊断;
2) 利用全局平均池化代替传统模型中的全连接层可以显著降低模型的计算量和过拟合风险,有利于模型应用于噪声较大和实时性要求较高的工业场景;
3) 采用随机破坏输入训练可以大大提升其训练后的抗噪能力,同时采用变化的破坏率效果好于固定的破坏率.
本研究主要针对智能诊断中的抗噪和计算复杂度高的问题,当前仅考虑转速不变情况下的故障诊断,但实际工程中转速是随时间不断变化,接下来的研究可以考虑将本文研究成果推广到变转速等复杂工况下的故障诊断.
| [1] |
JARDINE A K S, LIN D, BANJEVIC D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J]. Mechanical Systems & Signal Processing, 2006, 20(7): 1483. DOI:10.1016/j.ymssp.2005.09.012 |
| [2] |
GRAVES A, MOHAMED A R, HINTON G. Speech recognition with deep recurrent neural networks[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013: 6645
|
| [3] |
JIA F, LEI Y, LIN J, et al. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data[J]. Mechanical Systems & Signal Processing, 2016, 73(7): 303. DOI:10.1016/j.ymssp.2015.10.025 |
| [4] |
TAMILSELVAN P, WANG P. Failure diagnosis using deep belief learning based health state classification[J]. Reliability Engineering & System Safety, 2013, 115(7): 124. DOI:10.1016/j.ress.2013.02.022 |
| [5] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278. DOI:10.1109/5.726791 |
| [6] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]// International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc, 2012: 1097. DOI: 10.1145/3065386
|
| [7] |
SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]// IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 1
|
| [8] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770
|
| [9] |
WEN L, LI X, GAO L, et al. A new convolutional neural network based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5990. DOI:10.1109/Tie.2017.2774777 |
| [10] |
JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound & Vibration, 2016, 377(7): 331. DOI:10.1016/j.jsv.2016.05.027 |
| [11] |
INCE T, KIRANYAZ S, EREN L, et al. Real-time motor fault detection by 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7067. DOI:10.1109/Tie.2016.2582729 |
| [12] |
CHEN Z Q, LI C, SANCHEZ R V. Gearbox fault identification and classification with convolutional neural networks[J]. Shock & Vibration, 2015, 2015(2): 1. |
| [13] |
ZHANG W, PENG G, LI C, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors, 2017, 17(2): 425. DOI: ARTN 425 10.3390/s17020425 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5336047/
|
| [14] |
VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]// International Conference on Machine Learning. Helsinki: ACM, 2008: 1096
|
| [15] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010, 9(7): 249. |
| [16] |
TRA V, KIM J, KHAN S A, et al. Bearing fault diagnosis under variable speed using convolutional neural networks and the stochastic diagonal levenberg-marquardt algorithm.[J]. Sensors, 2017, 17(12): 2834. DOI: ARTN 2834 10.3390/s17122834 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5751511/
|
| [17] |
LOU X, LOPARO K A. Bearing fault diagnosis based on wavelet transform and fuzzy inference[J]. Mechanical Systems & Signal Processing, 2004, 18(5): 1077. DOI:10.1016/S0888-3270(03)00077-3 |
 2019, Vol. 51
2019, Vol. 51


