2. 重庆大学 机械工程学院 重庆 400044;
3. 重庆文理学院 机电工程学院 重庆 402160
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China;
3. College of Mechanical Engineering, Chongqing University of Arts and Sciences, Chongqing 402160, China
在产品设计过程中,元动作单元作为数控机床整机结构化分解的最小单元,其关键质量特性偏离目标值所带来的损失将反映到产品关键质量特性波动所带来的损失[1],所以控制产品设计过程中动作层关键质量特性的影响因素值, 使得关键质量特性波动值变小, 是整机设计质量控制研究的重点和基础.
目前,对产品设计过程中多质量波动的研究主要是针对多关键质量特性的稳健优化设计[2]. Yang等[3]采用一种极值分布(Extreme Value Distribution,EVD)的多关键质量特性稳健优化设计方法,利用多个关键质量特性之间的最大质量损失来解决质量损失相同的问题. Wan等[4]采用了一种灰色多项式混沌拓展(Grey Polynomial Chaos Extension,GPCE)方法处理不确定工程条件下产品多质量特性的变化与冲突问题.林晓华等[5]采用一种量词约束(Quantifier Constraint,QC)满足的方法解决了存在不确定因素的约束求解问题.韩云霞等[6]采用Kriging模型和稳健优化思想解决了稳健优化设计中噪声因子和可控因子波动对质量特性影响的问题.以上研究大都是针对影响因素或可控因子与关键质量特性之间的冲突影响关系,对于特定的优化问题不具有优势.
本文提出了一种三维质量屋优化的方法,增加了元动作单元维;采用ACCA对动作层影响因素进行了筛选;利用ERRT来协调影响因素、关键质量特性以及元动作单元三者之间的矛盾冲突;建立了以关键质量特性波动度为目标函数的优化数学模型,优化影响因素值,从而优化关键质量特性值.
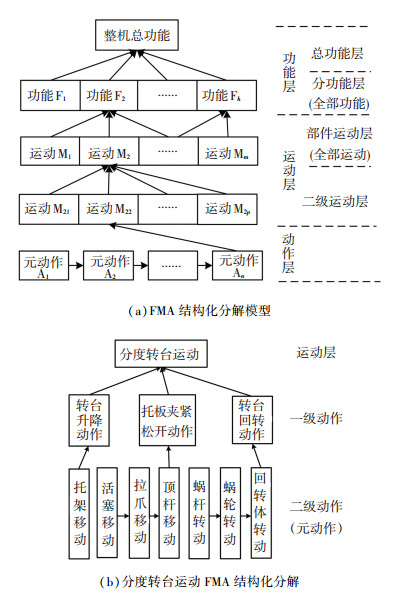
1 元动作理论基础 1.1 FMA结构化分解模型根据元动作理论,功能-运动-动作(Function-Movement-Action,FMA)结构化分解就是对机床的功能谱系进行研究,然后通过功能-运动-动作这样一个分解过程,将整机功能分解到运动的最小粒度——元动作[7], 分解过程如图 1所示.
|
图 1 FMA结构化分解模型 Fig. 1 FMA structured decomposition models |
FMA的核心思想是将数控机床的功能分成一系列最基本的与功能相对应的动作单元,通过对动作的性能特性的控制来保证整个数控机床各项功能和技术特性的实现,分解过程如图 1(a)所示.由于只是面向动作层的关键质量特性的优化,所以由图 1(a)可以得到端齿盘分度转台运动动作层的FMA结构化分解模型,如图 1(b)所示.
1.2 元动作单元元动作单元(Meta-Action Unit,MAU)是指由一个实现其规定功能的核心零件以及与该零件有支撑关系的一组零组件装配而成的独立单元,当给其一个动力源时便能够正常实现元动作的转动或移动,也可以对其进行独立的试验、测试和其他分析工作.
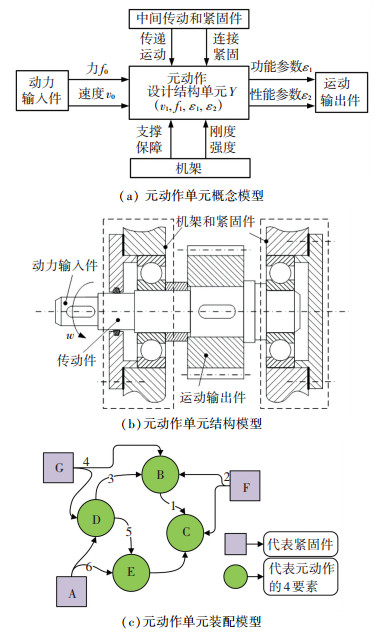
从运动学角度看,数控机床功能是将电机等动力输入转化为部件的加工运动,而元动作是实现数控机床功能的最基本的动作单元,其功能必然也是传递运动和力.因此,对于一个典型的元动作设计单元[8],它应该包含机架、动力输入件、运动输出件、中间传动件和紧固件5个组成要素,元动作单元的概念模型、结构模型和装配模型分别如图 2(a)、2(b)和2(c)所示.
|
图 2 元动作单元模型 Fig. 2 Meta-action unit models |
三维质量屋优化模型的3个维度分别为影响因素维x、元动作单元维y和关键质量特性维z.各维参数集合的确定过程如下所示:
1) x的确定.由于元动作单元是由一组零组件组成,所以产品设计过程中动作层关键质量特性影响因素很多,比如零件精度、装配精度等.此时采用ACCA[9]对所有的影响因素进行筛选,得到因素数N个,则动作层影响因素集合为X={x1,x2,…,xN}.
2) y的确定.假设某个运动包括L个元动作单元,则元动作单元集合记为Y={y1,y2,…,yL}.
3) z的确定.数控机床关键质量特性是从产品的客户需求中提取出来的,假设有M个关键质量特性,则关键质量特性集合为Z={z1,z2,…,zM}.由大量的提取经验可知,可靠性R、稳定性S、精度P、精度寿命A以及可用性U是影响数控机床的五大关键质量特性[10].其中R采用平均故障间隔时间r来度量;S采用机器能力指数s(机器能力指数[11]是指在工序稳定情况下制造设备所具有的保证产品质量的能力)来度量,取值必须≥1.33;P和A则分别采用精度值p和精度寿命值a来度量;可用性采用可用度u[12]来度量,可用度的取值范围为0~1,数值越大,表明机器的可用性越好.则关键质量特性维的参数集合为Z={r,s,p,a,u}.
三维质量屋优化模型的各个坐标轴都确定之后,建立优化模型如图 3所示.
|
图 3 三维质量屋优化模型 Fig. 3 3D house of quality optimization model |
动作层三维质量屋优化数学模型是利用ERRT得到各影响因素自相关矩阵、各个元动作单元关键质量特性与影响因素之间的关联矩阵和各个元动作单元性能之间的耦合矩阵,然后以关键质量特性波动度为目标函数,并在质量控制成本约束和开发时间约束下进行优化.
2.2.1 证据推理递归理论证据推理递归理论[13]是一种可对不确定信息进行表达和合成的推理理论.是利用信度函数表示证据,由于信度函数满足半可加性,因此与概率函数相比,信度函数更能表达信息的“不确定性”和“不知性”.
证据推理递归理论是在建立成员证据信念结构和团队证据信念结构的情况下,对所有属性的可信度进行递归融合,从而得到决策团队对目标对象的评价期望效用值.所以可以采用这种方式评价各影响因素之间的自相关性、各个元动作单元关键质量特性与影响因素之间的关联性以及各个元动作单元性能之间的耦合特性.
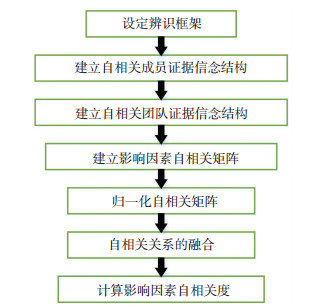
2.2.2 影响因素自相关关系函数动作层影响因素之间存在复杂的耦合依赖关系,建立影响因素自相关关系函数之前,首先需要采用ERRT建立影响因素自相关矩阵Φ,建立的具体的步骤如图 4所示.
|
图 4 影响因素自相关矩阵Φ的建立流程 Fig. 4 Process of establishing autocorrelation matrix Φ of influencing factors |
步骤1 设定辨识框架.设定影响因素自相关关系的评价等级G={G1,G2,G3,G4,G5}={强相关,相关,一般相关,弱相关,不相关}, 将其看作是辨识框架,并以数值标度简记为G={8,6,4,2,0}.
步骤2 建立自相关成员证据信念结构.按照评价信息转化规则[14],获得第l位QFD专家对在关键质量特性zi影响下,影响因素xj与影响因素xk之间的关联强度Tjkl, i的评价信息集ΘCj(Tjkl, i),并由此建立自相关强度评价的证据信念结构
| $ {S_{l,i,jk}}\left( {T_{jk}^{l,i}} \right) \mapsto \left\{ {\left( {{G_d},\chi _{jk,d}^{l,i}} \right),d = 1,2,3,4,5} \right\}. $ |
式中χjk, dl, i表示关键质量特性zi影响下,第l位专家将xj和xk之间的自相关强度Tjkl, i评价为Gd的信念度.
步骤3 建立自相关团队证据信念结构.将整个QFD团队对影响因素xj与影响因素xk之间的关联强度Tjkl, i的评价证据信念结构记为
| $ S_{j k}\left(T_{j k}^{i}\right) \mapsto\left\{\left(G_{d}, \chi_{j k, d}^{i}\right), d=1,2,3,4,5\right\}. $ |
其中:
步骤4 构建影响因素自相关矩阵.构建在关键质量特性zi影响下的自相关矩阵Ti=|Tjki|n×n,其中每个元素Tjki都是一个由团队决策的信念结构.相应的,对于关键质量特性QFD团队共构建n个影响因素自相关矩阵T1,… Ti,…, Tn.
步骤5 归一化自相关矩阵.按照加权的方式,可以得到一个统一的自相关矩阵,其计算公式为:
步骤6 自相关关系的融合.对于统一矩阵TO的每个元素TjkO而言,可以采用集合{Tjk1,Tjk2,…,Tjkn}作为其属性集合,然后利用证据推理算法获得TjkO的评价值.
步骤7 计算质量特性自相关度.计算QFD团队对TjkO的评价期望
按以上方式可得动作层的影响因素之间的自相关矩阵Φ,其中xi和xk的相关强度记为Φik,且ΦT=Φ.影响因素对关键质量特性波动的影响分为越大越好型和越小越好型,为建立统一的度量值,也为了表示影响因素对关键质量特性波动的影响程度,引入影响因素改进率的概念.在不考虑影响因素相互作用的情况下,第i个影响因素的越大越好型计划改进率Δxi1和越小越好型计划改进率Δxi2分别为式(1)和式(2):
| $ \Delta x_{i 1}=\frac{x_{i \max }-x_{i}}{x_{i \max }-x_{i \min }}, $ | (1) |
| $ \begin{array}{*{20}{c}} {\Delta {x_{i2}} = \frac{{{x_i} - {x_{i\min }}}}{{{x_{i\max }} - {x_{i\min }}}},}\\ {0 \le \Delta {x_i} \le 1,\quad i = 1,2, \cdots ,n.} \end{array} $ | (2) |
然而在实际设计过程中,影响因素之间存在相互作用关系,一个因素的改变会引起另一个因素的改变,引入实际改进率Δx′i来度量影响因素的波动.所以需要建立实际改进率和计划改进率之间的函数关系,故根据非线性关系的线性近似原理[15],可建立xi的实际改进率Δx′i与计划改进率Δxi的关系表达式:
| $ \Delta x_i^\prime = \sum\limits_{k = 1}^n \Delta {x_i}{\mathit{\Phi }_{ik}},i = 1,2, \cdots ,n, $ |
写成矩阵形式为
| $ \Delta \mathit{\boldsymbol{X'}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\Delta \mathit{\boldsymbol{X}}. $ | (3) |
建立元动作单元关键质量特性与影响因素之间的函数关系,必须先得到关键质量特性与影响因素的关联矩阵Q,令第l个元动作单元的关键质量特性与影响因素的关联矩阵为Ql, qlij为关键质量特性zli与影响因素xj的关联强度,采用证据推理递归理论得到的关联矩阵Ql的步骤如图 5所示:
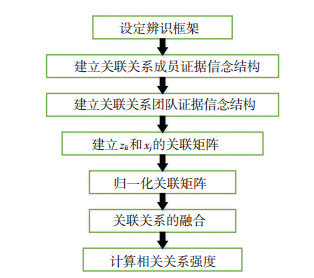
|
图 5 zli和xj的关联矩阵Ql的建立流程 Fig. 5 Process of establishing the correlation matrix Ql of zli and xj |
关联矩阵Ql的建立过程和影响因素自相关矩阵Φ的建立过程类似,不再赘述,最后得到关联矩阵Ql.为表示设计过程中产品质量特性的波动,引入质量特性波动率zlj的概念,质量波动率公式为
| $ z_{l j}=\frac{c_{l j}-c_{l j}^{*}}{c_{l j}^{*}}, j=1,2, \cdots, m_{l}, $ | (4) |
其中clj*为产品关键质量特性的目标值.
质量特性波动率的减小是通过改进影响因素实现的,故可建立二者之间的函数关系.与影响因素改进率相同,可以根据非线性关系的线性近似原理,建立关键质量特性波动率与影响因素的实际改进率关系表达式
| $ z_{l j}=\sum\limits_{i=1}^{n} q_{l i j} \Delta x_{i}^{\prime}, \quad j=1,2, \cdots, m_{l}, $ |
表示成矩阵形式为
| $ {\mathit{\boldsymbol{Z}}_l} = {\mathit{\boldsymbol{Q}}_l}\Delta \mathit{\boldsymbol{X'}} = {\mathit{\boldsymbol{Q}}_l}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\Delta \mathit{\boldsymbol{X}}. $ | (5) |
元动作是一种链式结构,各个元动作单元按照运动传递的方式进行连接,所以各个元动作性能之间存在一定的耦合依赖关系,在建立优化数学模型时,需要考虑这种耦合关系.
元动作单元性能耦合矩阵的建立方式和影响因素自相关矩阵的建立过程相同,通过分析计算可以得到元动作单元性能耦合矩阵为C.
2.2.5 优化数学模型的建立建立优化数学模型首先需要得到关键质量特性波动度目标函数,然后在质量控制成本约束和开发时间约束下进行优化.关键质量特性优化数学模型的建立过程如下所示.
1) 目标函数的建立.以关键质量特性波动度为目标函数就是考虑各维的冲突关系对动作层多关键质量特性的影响和最小,通过模糊层次分析法[16]求得第l个元动作单元关键质量特性的权重向量Wl,则目标函数为
| $ H = \mathit{\boldsymbol{C}}\sum\limits_{l = 1}^L {\sum\limits_{i = 1}^{{m_l}} {{w_{li}}} } \times {z_{li}} = \mathit{\boldsymbol{C}}\sum\limits_{l = 1}^L {{\mathit{\boldsymbol{W}}_l}} {\mathit{\boldsymbol{Q}}_l}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\Delta \mathit{\boldsymbol{X}}. $ |
2) 质量控制成本约束.考虑影响因素自相关关系影响的情况下,影响因素改进率与质量控制成本约束的关系为
| $ \begin{array}{l} E(x) = \sum\limits_{i = 1}^n {{e_i}} \left( {\Delta {e_i} - \sum\limits_{j \ne i}^n {{\mathit{\Phi }_{ij}}} \Delta {x_i}\Delta {x_j}} \right) \le B,\\ \;\;\;\;\;\;\;i = 1,2, \cdots ,n;\;\;\;\;\;l = 1,2, \cdots ,L. \end{array} $ |
式中ei为改善第l个影响因素xi的成本.
3) 开发时间约束.考虑影响因素自相关关系影响的情况下,影响因素改进率与开发时间约束的关系为
| $ \begin{array}{l} V(x) = \sum\limits_{i = 1}^n {{v_i}} \left( {\Delta {x_i} - \sum\limits_{j \ne i}^n {{\mathit{\Phi }_{ij}}} \Delta {x_i}\Delta {x_j}} \right) \le T,\\ \;\;\;\;\;\;\;\;i = 1,2, \cdots ,n;l = 1,2, \cdots ,L. \end{array} $ |
式中vi为改善第i个影响因素xi的开发时间.
4) 优化数学模型.综上所述,运动层多元关键质量特性优化数学模型为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\min H = \mathit{\boldsymbol{C}}\sum\limits_{l = 1}^L {{\mathit{\boldsymbol{W}}_l}{\mathit{\boldsymbol{Q}}_l}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\Delta \mathit{\boldsymbol{X}}} ,\\ {\rm{s}}.{\rm{t}}.\\ \;\;\;\;\;\;\;\;\;E\left( x \right) = \sum\limits_{i = 1}^n {{e_i}} \left( {\Delta {e_i} - \sum\limits_{j \ne i}^n {{\mathit{\Phi }_{ij}}} \Delta {x_i}\Delta {x_j}} \right) \le B,\\ \;\;\;\;\;\;\;\;\;V(x) = \sum\limits_{i = 1}^n {{v_i}} \left( {\Delta {x_i} - \sum\limits_{j \ne i}^n {{\mathit{\Phi }_{ij}}} \Delta {x_i}\Delta {x_j}} \right) \le T,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,n;l = 1,2, \cdots ,L. \end{array} $ |
通过上述优化数学模型的优化,可得动作层影响因素计划改进率向量
| $ \Delta \mathit{\boldsymbol{x}} = \left( {\Delta {x_1},\Delta {x_2}, \cdots ,\Delta {x_N}} \right). $ |
最后可以得到运动层最优影响因素向量以及最优关键质量特性向量为
| $ \mathit{\boldsymbol{X'}} = \left( {{{x'}_1},{{x'}_2}, \cdots ,{{x'}_N}} \right), $ |
| $ \mathit{\boldsymbol{Z'}} = \left( {{{z'}_1},{{z'}_2}, \cdots ,{{z'}_M}} \right). $ |
以某数控机床FMA分解模型中的端齿盘分度转台运动为例,建立面向动作层的三维质量屋优化模型,建立过程如下所示:
1) x的确定.通过ACCA提取到的动作层影响因素集为X={托架与活塞的同轴度x1,蜗轮的齿形误差x2,蜗杆的齿距积误差x3,托架套筒的内表面的表面粗糙度x4,活塞与顶杆的同轴度x5,蜗轮与蜗杆的垂直度x6}.活塞和与托架固联的套筒同轴装配,x1会影响托架的位置精度;x2、x3和x6会影响蜗轮蜗杆的传动精度、精度寿命以及性能的稳定性;x5会影响顶杆的位置精度;托架与O型圈进行密封装配,x4会影响密封稳定性.
2) y的确定.由图 1(b)可以得到Y ={蜗杆转动元动作单元y1,蜗轮转动元动作单元y2,回转体转动元动作单元y3,托架移动元动作单元y4,活塞移动元动作单元y5,拉爪移动元动作单元y6,顶杆移动元动作单元y7}.
3) z的确定.由2.1节可以得到分度转台运动的关键质量特性集合Z ={r,s,p,a,u}.经过对产品客户需求的提取以及量化,得到分度转台运动的平均故障间隔时间r为1 500 h,机器能力指数s为2.2,加工精度p为0.02 mm,精度寿命a为1 800 h,可用度u为0.6,则Z={1 500 h,2.2,0.02 mm,1 800 h,0.6}.
确定好三维质量屋的各维参数后,根据实验检测数据建立面向动作层的三维质量屋多关键质量特性优化框架模型如图 6所示.这里给出了y1的质量屋,采用模糊层次分析法得到:五大关键质量特性的权重向量W1=(0.35,0.12,0.22,0.20,0.11).
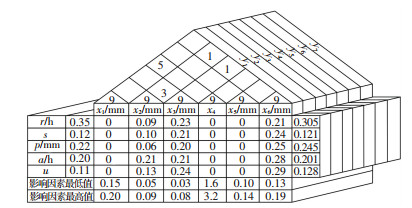
|
图 6 面向分度转台运动的多关键质量特性优化框架模型 Fig. 6 Optimization framework model of multiple key quality characteristics for indexing table motion |
4) 优化模型的建立.由图 6所示,可以通过归一化处理建立动作层6个影响因素之间的自相关矩阵
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{0.20}&0&0\\ 0&1&{0.33}&0&0&{0.20}\\ 0&{0.33}&1&0&0&{0.07}\\ {0.20}&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&{0.20}&{0.07}&0&0&1 \end{array}} \right]. $ |
根据历史数据与技术人员经验,采用ERRT建立y1关键质量特性与影响因素之间的关联矩阵
| $ {\mathit{\boldsymbol{Q}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{0.09}&{0.23}&0&0&{0.21}\\ 0&{0.10}&{0.21}&0&0&{0.24}\\ 0&{0.06}&{0.20}&0&0&{0.25}\\ 0&{0.21}&{0.21}&0&0&{0.28}\\ 0&{0.13}&{0.24}&0&0&{0.29} \end{array}} \right]. $ |
其他元动作单元关键质量特性与影响因素之间的关联矩阵Ql可以采用相同的方法得到.采用ERRT可得到元动作单元性能耦合矩阵
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&{0.21}&0&0&0&0&0\\ {0.21}&1&{0.31}&0&0&0&0\\ 0&{0.31}&1&{0.28}&0&0&0\\ 0&0&{0.28}&1&0&0&0\\ 0&0&0&0&1&{0.25}&0\\ 0&0&0&0&{0.25}&1&{0.34}\\ 0&0&0&0&0&{0.34}&1 \end{array}} \right]. $ |
在总的质量控制成本约束28万元和开发时间5 040 h的约束下,可以得到端齿盘分度转台运动的三维质量屋优化数学模型:
| $ \begin{aligned} \mathrm{OF} : \min H=& 0.1035 \Delta x_{1}+0.1526 \Delta x_{2}+0.2612 \Delta x_{3}+\\ & 0.2672 \Delta x_{4}+0.3698 \Delta x_{5}+0.2513 \Delta x_{6}, \end{aligned} $ |
| $ \begin{array}{l}{\text { s.t. }} \\ {\qquad \begin{aligned} E(x)=& 5 \Delta x_{1}+8 \Delta x_{2}+10 \Delta x_{3}+12 \Delta x_{4}+11 \Delta x_{5}+\\ & 8 \Delta x_{6}-2.3 \Delta x_{1} \Delta x_{4}-3.6 \Delta x_{2} \Delta x_{3}-\\ & 5.9 \Delta x_{2} \Delta x_{6}-1.2 \Delta x_{3} \Delta x_{6} \leqslant 28, \end{aligned}}\end{array} $ |
| $ \begin{array}{l} V(x) = 11\Delta {x_1} + 13\Delta {x_2} + 19\Delta {x_3} + 22\Delta {x_4} + 18\Delta {x_5} + \\ \;\;\;\;\;\;\;\;\;\;16\Delta {x_6} - 5.7\Delta {x_1}\Delta {x_4} - 7.9\Delta {x_2}\Delta {x_3} - \\ \;\;\;\;\;\;\;\;\;\;11.2\Delta {x_2}\Delta {x_6} - 9.8\Delta {x_3}\Delta {x_6} \le 5040{\rm{h}}{\rm{.}} \end{array} $ |
式中: 0≤Δxi≤1, i=1,2,…,6.
最后利用Mathprogram软件进行优化求解,优化后的结果如表 1所示.
| 表 1 优化结果 Tab. 1 Optimization results |
根据式(3)得到动作层影响因素实际改进率为ΔX′=(-0.05,0.25,-0.56,-0.37,-0.1,0.79);再根据式(1)和式(2)得到影响因素取值的最优解为X′=(0.161 mm,0.060 mm,0.046 mm,2.256(取1.6),0.109 mm,0.146 mm),再根据式(4)和式(5)可得端齿盘分度转台运动的关键质量特性优化值为Z′=(1 526 h,2.5,0.023 mm,1 856 h,0.78),即优化得到的r为1 526 h、s为2.5、p为0.023 mm、a为1 856 h以及u为0.78时,此时的关键质量特性波动最小.
分别选取6组不同的分度转台运动的影响因素值,在相同条件下运转4 000 h,然后通过记录的故障数据以及检测结果计算得到五大关键质量特性值,与初始数据进行对比,计算关键质量特性波动度值,实验结果如表 2所示
| 表 2 实验结果 Tab. 2 Experimental results |
根据表 2的实验结果,考虑端齿盘分度转台运动的质量控制成本以及质量开发时间,可以看出,当影响因素取优化值时,此时的关键质量特性波动度最小,可见优化的结果是合理的,即该优化模型是合理有效的.
4 结论1) 本文对传统二维质量屋进行了拓展,提出了三维质量屋优化模型,增加元动作单元维,用于解决动作层多关键质量特性的优化问题.
2) 采用ACCA对动作层影响因素进行了筛选,提取出了对端齿盘分度转台运动关键质量特性影响较大的影响因素.
3) 利用ERRT建立了影响因素自相关矩阵、各元动作单元关键质量特性与影响因素的关联矩阵、各元动作单元之间的性能耦合矩阵.
4) 最后通过实例分析和实验验证了三维质量屋优化模型的合理性和有效性.
| [1] |
张根保, 任显林, 刘立堃, 等. 面向制造过程的产品多关键质量特性优化模型[J]. 计算机集成制造系统, 2010, 16(6): 1286. ZHANG Genbao, REN Xianlin, LIU Likun, et al. Multiple key quality characteristics optimization model for manufacturing process[J]. CIMS, 2010, 16(6): 1286. DOI:10.13196/j.cims.2010.06.168.zhanggb.026 |
| [2] |
何桢, 吕海利. 多元质量特性稳健性设计方法的优化研究[J]. 管理科学, 2007, 20(1): 2. HE Zhen, LV Haili. Optimization of robust design method for multivariate quality characteristics[J]. Management Science, 2007, 20(1): 2. DOI:10.3969/j.issn.1672-0334.2007.01.001 |
| [3] |
YANG C, DU X. Robust design for multivariate quality characteristics using extreme value distribution[J]. Journal of Mechanical Design, 2014, 136(10): 101405. DOI:10.1115/1.4028016 |
| [4] |
WAN L, CHEN H, OUYANG L, et al. Multi-quality characteristics robust optimization design based on grey-PCE for complex equipment products[J]. Systems Engineering & Electronics, 2018, 32(12): 269. |
| [5] |
林晓华, 冯毅雄, 谭建荣, 等. 基于量词约束满足的机械产品质量特性稳健优化设计方法[J]. 机械工程学报, 2013, 49(15): 169. LIN Xiaohua, FENG Yixiong, TAN Jianrong, et al. Robust optimal design method for mechanical product quality characteristics based on quantifier constraint satisfaction[J]. Journal of Mechanical Engineering, 2013, 49(15): 169. DOI:10.3901/JME.2013.15.169 |
| [6] |
韩云霞, 马义中, 欧阳林寒, 等. 基于两类因子波动下的稳健优化设计[J]. 工业工程与管理, 2017, 22(6): 25. HAN Yunxia, MA Yizhong, OUYANG Linhan, et al. Robust optimal design based on two kinds of factor fluctuations[J]. Industrial Engineering and Management, 2017, 22(6): 25. DOI:10.19495/j.cnki.1007-5429.2017.06.004 |
| [7] |
朱国云, 刘英, 张根保, 等. FMA结构化分解驱动的加工中心设计过程规划[J]. 机械科学与技术, 2017, 36(8): 1167. ZHU Guoyun, LIU Ying, ZHANG Genbao, et al. Design process planning of machining center driven by FMA structured decomposition[J]. Mechanical Science and Technology, 2017, 36(8): 1167. DOI:10.13433/j.cnki.1003-8728.2017.0804 |
| [8] |
朱国云.基于元动作单元的加工中心设计过程耦合与解耦技术研究[D].重庆: 重庆大学, 2017 ZHU Guoyun. Study on coupling and decoupling technology of machining center design process based on meta-actuation unit[D]. Chongqing: Chongqing University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10611-1017838535.htm |
| [9] |
ZHU F, WANG H. An ant colony optimisation algorithm for aggregated multicast based on minimum grouping model[J]. International Journal of Communication Systems, 2013, 26(3): 277. DOI:10.1002/dac.v26.3 |
| [10] |
冉琰.机电产品元动作单元建模及关键质量特性预测控制技术研究[D].重庆: 重庆大学, 2016 RAN Yan. Research on modeling of meta-actuation unit and predictive control technology for key quality characteristics of mechanical and electrical products[D]. Chongqing: Chongqing University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10611-1017801788.htm |
| [11] |
罗孟然, 丛明, 顾齐芳, 等. 基于Cmk分析的加工中心精度稳定性评估[J]. 组合机床与自动化加工技术, 2015(3): 149. LUO Mengran, CONG Ming, GU Qifang, et al. Accuracy stability evaluation of machining center based on cmk analysis[J]. Combined Machine Tool and Automatic Machining Technology, 2015(3): 149. |
| [12] |
李小兵, 杨兆军, 李国发, 等. 基于函数性数据分析的数控机床瞬时可用度建模[J]. 吉林大学学报(工), 2012, 42(5): 1151. LI Xiaobing, YANG Zhaojun, LI Guofa, et al. Modeling of instantaneous availability of CNC machine tools based on functional data analysis[J]. Journal of Jilin University(Technology), 2012, 42(5): 1151. DOI:10.13229/j.cnki.jxbgb2012.05.005 |
| [13] |
丁力平.面向质量特性的定制产品稳健设计技术及其应用研究[D].浙江: 浙江大学, 2010 DING Liping. Research on robust design technology and its application for custom-made products based on quality characteristics[D]. Zhejiang: Zhejiang University, 2010 http://cdmd.cnki.com.cn/article/cdmd-10335-1011068987.htm |
| [14] |
南刚, 王亚民, 陈希. 基于多维度模糊语言信息的移动服务质量测评方法[J]. 工业工程与管理, 2014, 19(2): 81. NAN Gang, WANG Yamin, CHEN Xi. Mobile quality of service evaluation method based on multi-dimensional fuzzy language information[J]. Industrial Engineering and Management, 2014, 19(2): 81. DOI:10.19495/j.cnki.1007-5429.2014.02.014 |
| [15] |
高潮, 任光. DC-DC开关变流器的小信号线性近似分析方法[J]. 深圳信息职业技术学院学报, 2003(1): 11. GAO Chao, REN Guang. A small signal linear approximate analysis method for DC-DC switching converter[J]. Journal of Shenzhen Institute of Information Technology, 2003(1): 11. DOI:10.3969/j.issn.1672-6332.2003.01.004 |
| [16] |
夏毅敏, 卞章括, 胡承欢, 等. 复合式土压平衡盾构机刀盘性能综合评价方法[J]. 机械工程学报, 2014, 50(21): 1. XIA Yimin, BIAN Zhangkuo, HU Chenghuan, et al. A comprehensive evaluation method for the cutter performance of composite earth pressure balance shield machine[J]. Journal of Mechanical Engineering, 2014, 50(21): 1. DOI:10.3901/JME.2014.21.001 |
 2019, Vol. 51
2019, Vol. 51


