2. 武汉大学 动力与机械学院,武汉 430072
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
硅材料作为重要的工业材料,是半导体行业微机电系统的主要原材料,构成现代电子信息和计算机产业的基石[1].硅分布广泛、含量丰富、成本低廉、加工技术成熟,随着近来可再生能源需求的日益扩大,硅基材料也尝试于热电材料领域的应用[2].由于硅材料在工业上的广泛应用,对其热性能的研究备受关注[3].材料的导热和散热对于设备的性能有着重要影响[4],对于计算机处理器要求高导热系数,以尽快移走多余的热量,而对于热电材料则需要导热系数尽量小[5].材料中不可避免出现的天然缺陷结构会破坏材料的对称性,引起声子在缺陷处的散射,影响材料的导热性能[6].因此研究材料微观结构对材料热输运性质的影响成为广受关注并极具兴趣的研究领域[7].
分子动力学作为从分子/原子的微观层面进行研究的一种重要方法,通过对体系微观细节的计算获取工程关心的宏观参数[8].采用分子动力学模拟可以有效地将影响材料导热性能的各种因素独立出来,为从微观角度更深入地理解材料的热输运性质提供帮助[9].文献[6, 10-11]分别应用平衡和非平衡分子动力学方法对Si材料热导率进行对比模拟研究.文献[12]应用平衡分子动力学方法探讨1 000 K温度下不同空位缺陷浓度对Si材料热导率的影响,并给出小缺陷浓度(< 1%)时相对热阻增量与空位浓度呈线性关系.文献[13]应用平衡分子动力学方法模拟研究了0.1%单空位浓度对热导率的影响,发现随温度升高,空位对热导率的影响程度减小.文献[6]中采用加入依赖时间扰动项的非平衡分子动力学方法,研究了700 K、1 000 K温度下不同空位浓度对Si材料热导率的影响,发现热导率随空位浓度增加而降低.文献[2, 7]采用逆非平衡分子动力学方法分别模拟300 K、500 K温度下空位缺陷结构对Si材料热导率的影响,发现缺陷结构的存在极大地减小了声子散射的平均自由程,从而降低了材料的导热性能,高频声子与缺陷间的散射是热导率降低的主要原因.以上文献多为考虑单一温度或单一浓度的空位缺陷结构对热导率的影响,对于综合考虑温度、缺陷浓度对热导率的影响以及点缺陷结构中另一种重要的间隙原子类型[14-15]影响热导率的情况则少有报道,对宏观量热导率及热阻增量与微观量声子散射平均自由程间的关系也缺少相关深入的分析讨论.
由于非平衡法比平衡法更节约计算时间[2, 10]且更利于模拟缺陷结构的热导率[6],逆非平衡分子动力学在计算材料热导率方面具有更高的效率[16],本文采用逆非平衡分子动力学方法,综合考虑不同温度、不同点缺陷浓度的空位结构以及Si间隙原子中被广为研究[17]且形成能最低、最易于出现的四面体间隙位[18]对Si材料热导率的影响,更充分地研究材料热导率受各因素影响的改变.进而本文对两种类型点缺陷对材料热导率的影响进行比较分析,针对点缺陷影响Si材料热导率的情况进行更全面的探讨.鉴于分子动力学在微观层面研究方法上的优势,本文通过对模拟结果的分析,将声子散射分为声子间散射与声子、缺陷散射,更为深入地讨论温度与点缺陷浓度对声子间散射和声子、缺陷散射的影响情况,揭示出宏观上点缺陷产生的相对热阻增量实质为微观层面声子间散射与声子、缺陷散射平均自由程的比值,为进一步的研究提供参考.
1 模型构建与模拟细节 1.1 热导率与热导率模拟的有限尺度效应物质的热导率κ表征材料的导热性能.一维导热的傅里叶定律可由式(1)表示为
| $ \kappa=-\frac{J_{z}}{\frac{\mathrm{d} T}{\mathrm{d} z}}. $ | (1) |
式中:假定z方向为热流生成方向;Jz为通过z方向的热流密度,即体系稳态时单位时间垂直通过单位截面积的热量;
| $ \kappa=\frac{1}{3} c_{v} \cdot v \cdot l. $ | (2) |
式中:cv为单位体积的比热,v为声子的方均根速率,l为声子间散射的平均自由程.
热导率的分子动力学模拟研究表明当材料模拟体系尺度小于或接近材料中声子间散射的平均自由程时,由于声子在热源、冷源界面的散射作用,特定尺度模拟体系的热导率有随体系中热流生成方向的尺度改变而改变的尺度效应现象[10, 20].对于非平衡分子动力学的热导率模拟,文献[10]通过式(3)作为存在尺度效应时声子的有效平均自由程:
| $ \frac{1}{l_{\mathrm{eff}}}=\frac{1}{l_{\infty}}+\frac{4}{L_{z}}. $ | (3) |
式中: leff为声子的有效平均自由程,l∞为体系无限大时声子间散射的平均自由程(体材料的声子平均自由程),Lz为体系在热流生成z方向的尺度.
将热导率的微观表达式(2)中取l为leff并将式(3)代入得热导率κ与热流生成方向模拟体系尺度Lz间的关系式(4)[10]:
| $ \frac{1}{\kappa}=\frac{a^{3}}{4 k_{B} v}\left(\frac{1}{l_{\infty}}+\frac{4}{L_{z}}\right). $ | (4) |
式中:a为材料的晶格常数,kB为玻尔兹曼常数(kB= 1.38 × 10-23 J/K),v为材料内声子的群速度.等号右侧的括号内即为有效平均自由程倒数1/leff.体相材料的热导率采用外推法由式(4)中1/κ与1/Lz间的线性关系外推体系尺度,取Lz→ ∞(1/Lz→ 0)的极限得到.
1.2 模型构建与逆非平衡分子动力学方法模拟过程应用分子动力学经典的大规模分子并行计算模拟器[21](LAMMPS,Large-scale Atomic/Molecular Parallel Simulator)实现.先构建沿热流方向不同尺度的模拟体系,采用逆非平衡分子动力学方法(rNEMD)由式(1)计算各体系的热导率,再根据式(4)对不同尺度各体系热导率的模拟结果应用外推法得到体相Si晶体材料的热导率.
取z方向为热流生成方向构建5个沿该方向不同尺度的模拟体系,尺度分别为100a0、150a0、200a0、250a0、300a0(54.31、81.46、106.81、135.77、162.91 nm),a0为Si晶体材料的晶格常数5.430 7 Å.所有体系垂直热流方向的截面(x × y)尺度均固定为4a0 × 4a0(2.17 × 2.17 nm2).相应模拟体系的原子数分别为12 800、19 200、25 600、32 000、38 400.体系各方向x、y、z采用周期性边界条件(PBC,periodic boundary condition). Si原子间的相互作用应用Stillinger-Weber (SW)[22]势能描述.
rNEMD方法通过交换原子速度生成热流产生相应温度梯度,该方法热导率模拟的体系结构如图 1所示.所有模拟体系沿z方向平均分为200等份,形成200个子区域.每100步交换中间子区域(第101号子区域,图 1中h处)速度最小原子与材料一端处(1号子区域,图 1中c处)速度最大原子的速度.中间子区域由于原子的速度逐渐增大温度升高成为热源,1号子区域由于原子速度减小成为冷源.该人为交换原子产生由冷源至热源的热流与体系由此自发导热产生的热源至冷源的热流逐渐平衡,体系相应地达到稳态并具有稳定的热流及温度分布.

|
图 1 rNEMD方法模拟体系热导率图示 Fig. 1 The schematic of a simulation sample used for thermal conductivity calculation by rNEMD method |
体系达稳态后的稳态热流密度Jz通过式(5)计算单位时间、单位截面积体系中交换原子速度产生的净动能得到:
| $ J=\frac{\sum\limits_{n}\left(\frac{1}{2} m v_{\text { high }}^{2}-\frac{1}{2} m v_{\text { low }}^{2}\right)}{2 A t}. $ | (5) |
式中:vhigh、vlow分别为冷源中速度最快原子、热源中速度最慢原子的速度,分子中的求和表示稳态体系n次原子速度交换产生的总净动能;t为n次原子速度交换对应的时间;A为垂直原子速度交换方向的截面积.式(5)分母中的因子2表示由于z方向的周期性边界条件,体系中的热流相背向两个方向流动(见图 1).
稳态体系的温度分布基于经典统计物理的配分函数理论由式(6)计算各子区域j内的温度Tj得到:
| $ \frac{3}{2} n_{j} k_{B} T_{j}=<\sum\limits_{i=1}^{n_{j}} \frac{1}{2} m_{i} v_{i}^{2}>. $ | (6) |
式中:nj为第j个子区域中的原子数;kB为玻尔兹曼常数;mi为子区域j中第i个原子的质量;vi为原子i的速度;<>表示取子区域j中对应式(5)模拟时间t内的原子总动能的平均值;Tj为模拟时间t内子区域j的平均温度.
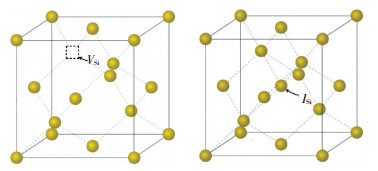
对于体系含点缺陷结构的热导率模拟,通过在完整晶体结构中删除和增加一定比例的原子分别实现对空位缺陷(VSi)和间隙原子(ISi)的模型构建.间隙原子考虑各间隙位置中形成能最低的四面体间隙位[18],如图 2所示.
|
图 2 Si晶体的空位缺陷(VSi)与四面体间隙位的间隙原子(ISi)结构图示 Fig. 2 The schematic structure of Si crystal with vacancy (VSi) and tetrahedral interstitial(ISi) |
由于原子速度的交换会引起热源、冷源内非物理的声子散射[3, 23],缺陷构建在图 1所示与热源、冷源有一定距离的m区域内(图 1中b区域表示热源、冷源与缺陷构建区域间的缓冲区域,各b区域占10个子区域).以n表示点缺陷的浓度,空位浓度(nv)和间隙原子浓度(ni)为删除或增加的原子数占m区域总原子数的比例.含点缺陷结构Si晶体的热导率模拟过程与完整晶体的情况相似,构建4个沿热流生成z方向不同尺度的模拟体系,由式(4)外推得到含点缺陷结构材料的体相热导率. 4个模拟体系沿z方向的尺度为100a0、150a0、200a0、250a0,截面x、y方向的尺度与完整晶体相同.
1.3 模拟过程所有模拟体系的各模拟过程均采用0.25 fs的时间步长.通过改变体系内原子的不同初始速度分布,对每个尺度的模拟体系进行2~3次独立模拟计算.各模拟体系先采用Nose-Hoover温度控制算法进行0.1 ns的正则系综(NVT)弛豫过程,以达到稳定的预期模拟温度.之后应用rNEMD方法在微正则系综(NVE)内每100步交换一次热源、冷源中的原子速度形成稳定热流,共持续0.725 ns.由于初始交换原子速度产生热流时体系未达稳态,各子区域内温度波动较大,因此忽略此时间内的数据,取模拟过程后0.575 ns内(即式(5)中的模拟时间t)体系已处于稳态阶段中的热流和温度数据进行热导率计算.
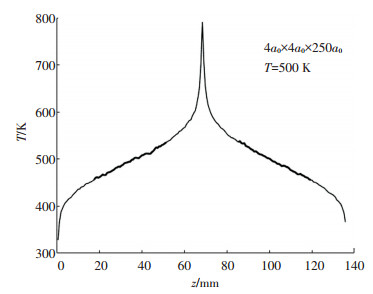
2 模拟结果 2.1 完整Si晶体的热导率模拟结果图 3所示为完整Si晶体由式(6)计算各子区域平均温度的温度分布图示,其中模拟温度T=500 K,模拟体系尺度为4a0 × 4a0 × 250a0.图中沿z方向距离模拟体系热源及冷源较远处的大部分区域温度分布呈线性,热源、冷源附近的区域则由于交换原子速度形成强烈的非物理声子散射使得温度分布呈非线性状[2, 7].取图 3距热源、冷源较远处深色部分近似线性的温度分布区间(模拟体系z方向总长12%~38%、62%~88%的部分)得两段区间的温度梯度分别为2.25 K/nm、2.38 K/nm.根据体系热流密度的计算式(5)及傅里叶定律式(1)得此体系500 K温度下热导率的模拟结果为56.09±1.59 W· m-1·K-1.
|
图 3 应用rNEMD方法模拟完整Si晶体材料热导率,沿热流生成z方向的温度分布图示.图中深色部分为计算温度梯度所截取的线性温度分布区间 Fig. 3 The temperature profile of the sample along z direction by rNEMD method for the thermal conductivity calculation. The bold linear regions of the temperature profile are adopted to calculate the temperature gradient |
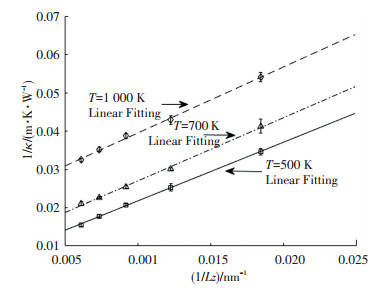
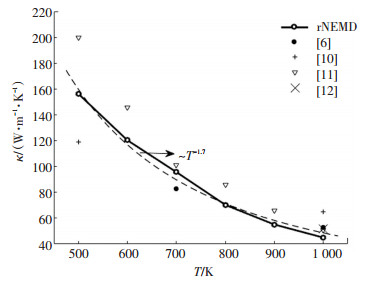
根据尺度效应,对完整晶体的模拟体系,不同温度各体系热导率模拟结果的倒数1/κ与热流生成z方向尺度倒数1/Lz间的关系示于图 4.图中不同温度下1/κ与1/Lz间均呈近似线性的关系,与式(4)一致.各近似线性关系经线性拟合后所得斜率分别为1.54×10-9 m2K/W(500 K)、1.65×10-9 m2K/W(700 K)、1.73×10-9 m2K/W(1 000 K).文献[10]中根据Si有关物理量计算得出式(4)线性关系斜率的理论值为1.8×10-9 m2K/W,模拟结果与理论结果相近. Si晶体材料的热导率根据1/κ与1/Lz间的线性关系,由各尺度外推至1/Lz→0时的极限得到. 图 5所示为各模拟温度T下,体相完整Si晶体热导率κ以及相关文献采用相同势函数的模拟结果.图中rNEMD的结果为本文逆非平衡方法的模拟结果;文献[10-11]为传统非平衡方法的模拟结果;文献[6]为引入依赖时间扰动项的非平衡方法的模拟结果,文献[12]为平衡分子动力学方法的模拟结果.本文的模拟结果与文献结果基本吻合.由于当外推后的热导率结果较大时,1/κ与1/Lz间线性拟合中很小的误差即可产生较大的外推误差[10],在温度相对较低时,模拟结果间存在一定偏差.由(4)式当1/Lz→0时,有
|
图 4 不同温度rNEMD方法模拟宏观体相Si晶体热导率1/κ与1/Lz的线性关系 Fig. 4 The linear relationships between 1/κ and 1/Lz for calculating the thermal conductivity of bulk Si crystal by rNEMD method under various temperature conditions |
|
图 5 各模拟温度下体相Si晶体材料热导率的模拟结果 Fig. 5 The calculated thermal conductivities of bulk Si crystal under various simulation temperatures |
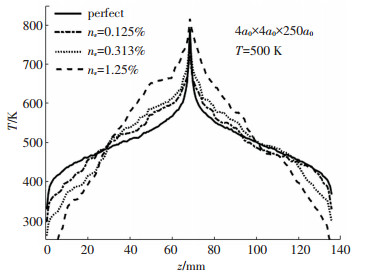
体系中引入空位缺陷、间隙原子的方法如1.2所述.模拟过程和热导率的计算方法与完整晶体的情况相同. 图 6所示为含不同空位缺陷浓度500 K温度下,体系尺度为4a0 × 4a0 × 250a0的温度分布.空位缺陷的存在极大地增加了体系温度分布中线性区间的斜率,并且随空位浓度的增加,体系中的温度梯度逐渐增大.对于引入间隙原子的情况,体系中的温度分布同样具有随间隙原子浓度增加而温度梯度增大的结果.
|
图 6 模拟温度为500 K, 模拟体系尺度为4a0 × 4a0 × 250a0含不同空位浓度nv的Si晶体沿热流生成z方向的温度分布图示 Fig. 6 The temperature profiles of the samples in z direction with various nv and fixed box size of 4a0 × 4a0 × 250a0 at the simulation temperature of 500 K |
考虑到声子平均自由程主要受到声子之间散射、声子与样品边界散射及声子与缺陷或杂质散射的影响,声子的总平均自由程可表示为式(7)[27]:
| $ \frac{1}{l}=\frac{1}{l_{p}}+\frac{1}{l_{b}}+\frac{1}{l_{d}}. $ | (7) |
式中:l为总平均自由程,lp为声子与声子间散射的平均自由程,lb为声子与界面散射的平均自由程,ld为声子与缺陷或杂质散射的平均自由程.对于含点缺陷的情况,式(3)中的有效平均自由程应增加缺陷散射的因素满足式(8).代入式(4)得含点缺陷情况1/κ与1/Lz的关系式(9).当1/Lz→0时,含缺陷的体相硅晶体热导率κ满足关系式:
|
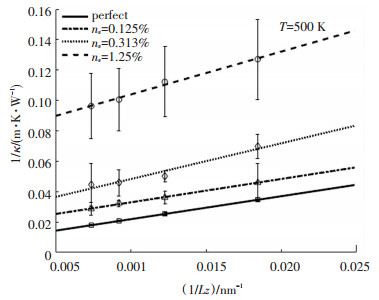
图 7 500 K温度,含不同空位浓度nv外推体相Si晶体热导率时1/κ与1/Lz的线性关系 Fig. 7 The linear relationships between 1/κ and 1/Lz for extrapolating the thermal conductivity of bulk Si crystal with various concentrations of vacancy |
| $ \frac{1}{l_{e f f}}=\frac{1}{l_{\infty}}+\frac{4}{L_{z}}+\frac{1}{l_{d}}, $ | (8) |
| $ \frac{1}{\kappa}=\frac{a^{3}}{4 k_{B} v}\left(\frac{1}{l_{\infty}}+\frac{4}{L_{z}}+\frac{1}{l_{d}}\right). $ | (9) |
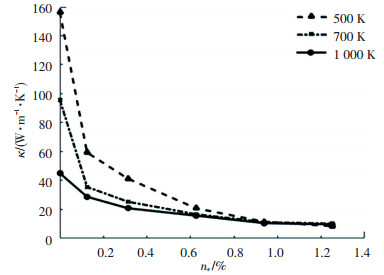
不同温度含不同空位缺陷浓度nv及间隙原子浓度ni的Si晶体体相热导率κ分别示于图 8(a)、(b)中.各温度下κ均随nv和ni的增加而减小.低点缺陷浓度时,材料的热导率大幅降低,随缺陷浓度的增加,热导率下降幅度减少.各温度下,0.25%的点缺陷浓度已使材料的热导率降低一半以上,相对较高缺陷浓度时(n>0.8%)热导率基本不再降低,稳定在低导热性能的状态. 图 8(a)中作为对照也给出文献[12]应用平衡法模拟含不同空位缺陷浓度1 000 K温度下Si热导率的相关结果.随着空位缺陷和间隙原子浓度的增加,温度对热导率的影响逐渐减小.较高点缺陷浓度时,各温度的热导率趋于同一较低数值,温度对热导率不再具有影响.考虑到温度主要影响声子之间的散射自由程l∞,而声子、缺陷散射自由程ld主要受缺陷浓度影响,随缺陷浓度增加,ld相对更大程度地减小,温度影响l∞对热导率的作用则逐渐减弱.对l∞和ld更为具体的量化分析在3.2中有相应讨论.

|
图 8a 不同温度Si的体相热导率与空位缺陷浓度nv的关系 Fig. 8a The calculated bulk thermal conductivity as functions of the concentration of nv at various temperatures |
|
图 8b 不同温度Si的体相热导率与间隙原子浓度ni的关系 Fig. 8b The calculated bulk thermal conductivity as functions of the concentration of ni at various temperatures |
应用rNEMD方法进行热导率模拟时,由尺度效应,各体系的热导率与热流方向的体系尺度间有关系式(4).为更充分了解并验证rNEMD方法对材料热导率的模拟过程和结果,本节针对体系中热流大小、垂直热流方向的体系尺度、子区间划分程度和时间步长等各重要参数对模拟结果的影响进行有关讨论.
3.1.1 体系中生成热流的影响改变rNEMD方法中原子速度交换的时间间隔可调整体系内生成热流的大小.这里在相同尺度的体系内生成不同大小的热流,通过比较各体系的热导率模拟结果对热流的影响情况进行探讨.
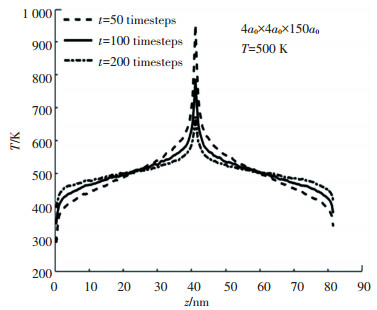
表 1所示为各模拟体系中生成不同热流密度稳态时的热导率结果.模拟体系为完整晶体,温度为500 K,x、y、z方向的晶胞数均为4、4、150,z方向为热流生成方向.交换原子速度的时间间隔t越大,稳态体系中的热流密度J越小. 图 9为不同t对应的温度分布.如图所示,温度分布随t的增加逐渐平缓,温度梯度随体系内热流减小逐渐减小. 表 1的结果表明在所取t的改变范围内,体系中生成热流的大小对热导率的模拟结果不具有显著影响.本文热导率的模拟过程中,采用rNEMD方法每100步交换原子速度的参数进行.与表 1中数据比较,模拟结果的波动较小(< 10%),模拟结果认为具有相当的准确性.
| 表 1 体系中生成热流密度大小对模拟结果的影响(500 K) Tab. 1 The effect of thermal flux in sample on simulation results (500 K) |
|
图 9 不同原子速度交换时间间隔t的温度分布(500 K) Fig. 9 Temperature distributions with various time intervals of atomic velocity exchange(t) (500 K) |
这里通过固定模拟体系沿热流生成方向的尺度,调整体系的横截面积大小探讨垂直热流方向的体系尺度对热导率模拟结果的影响.
模拟结果如表 2所示.各模拟体系均为完整晶体,温度为500 K,z方向的晶胞数固定为150.为控制单一变量,调整各体系内生成相近的热流密度J.如表 2所示,垂直热流方向横截面积的变化对模拟结果不造成很大影响.这是由于周期性边界条件的设置,使得声子在体系垂直热流方向的横截面上可以自由运动而不发生边界散射的结果.
| 表 2 垂直热流方向横截面积对模拟结果的影响(500 K) Tab. 2 The effect of cross section areas on simulation results (500 K) |
表 3所示为完整晶体500 K温度下沿热流生成z方向不同子区间划分数目的热导率模拟结果.模拟体系x、y、z方向的晶胞数均为4、4、150.沿热流方向子区间分割的精度会影响获取体系温度分布后温度梯度计算的精度,但由于计算温度梯度的数据均取自体系达稳态后所形成的稳定的温度分布,如表 3所示子区间的分割精度不明显影响相应的热导率模拟结果.
| 表 3 热流方向子区间分割精度的影响(500 K) Tab. 3 The effect of dividing degree of the sample along the direction of heat flux on simulation results (500 K) |
时间步长作为分子动力学模拟中的一个重要参数,为准确描述各原子在一周期内的确定位置,通常时间步长选取为小于原子最小振动周期的1/10. 表 4所示为500 K温度下,体系x、y、z尺度为4、4、150个晶胞的完整晶体在不同时间步长设置下的模拟结果.为控制单一变量,各体系内调整生成相近的热流密度J. 表 4中的结果表明,在所考虑的时间步长范围内,热导率模拟结果的波动很小,不同的时间步长对模拟结果不具有较大影响.
| 表 4 时间步长对模拟结果的影响(500 K) Tab. 4 The effect of time step on simulation results (500 K) |
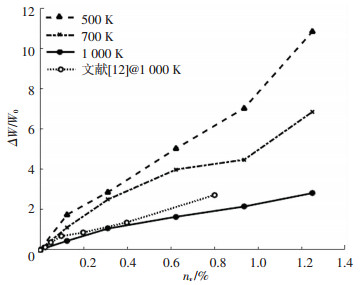
文献[12]应用平衡分子动力学方法研究1 000 K温度下Si晶体的相对热阻增量ΔW/W0与空位缺陷浓度nv的关系,发现低浓度(nv < 1%)时ΔW/W0与nv成线性关系.热阻W为热导率κ的倒数(W=1/κ),ΔW为有点缺陷存在的热阻(Wd)相对完整晶体热阻(W0)的热阻增量,ΔW/W0为相对热阻增量. 图 10为几种温度下点缺陷产生的相对热阻增量与点缺陷浓度的关系图示,图 10(a)为空位缺陷浓度nv的结果(文献[12]平衡法的结果作为对照),图 10(b)为间隙原子浓度ni的结果.如图 10可见,与点缺陷降低材料热导率相对应,各温度下随点缺陷浓度的增加,热阻逐渐增加,ΔW/W0与两种点缺陷结构在所考虑浓度范围内均呈近似线性增加的关系.随温度升高,ΔW/W0与nv和ni间线性关系的斜率降低,相同点缺陷浓度对材料热阻增加的影响逐渐减弱.
|
图 10(a) 不同温度的相对热阻增量ΔW/W0与空位缺陷浓度nv的关系 Fig. 10(a) The relative additional thermal resistivity ΔW/W0 as functions of nv at various temperatures |
|
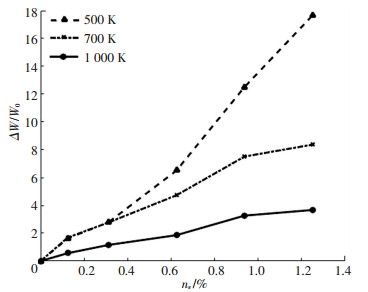
图 10(b) 不同温度的相对热阻增量ΔW/W0与间隙原子浓度ni的关系 Fig. 10(b) The relative additional thermal resistivity ΔW/W0 as functions of ni at various temperatures |
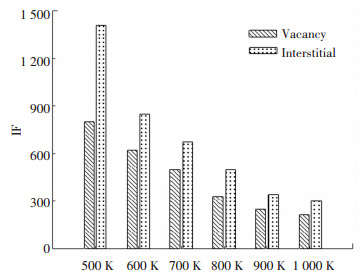
在所有考虑的缺陷浓度范围内,取ΔW/W0与nv和ni间近似线性关系的斜率作为衡量两种点缺陷对材料热阻影响程度的影响因子(IF),如图 11所示. 图 11中随温度升高两种点缺陷的影响因子均逐渐减小,点缺陷对热阻增加(热导率降低)的影响程度随温度的升高逐渐减小. 图 11也表明相同温度下间隙原子均比空位缺陷具有更高的影响因子,间隙原子对热阻的增加(热导率降低)有相对更大的影响. 500 K时两种点缺陷结构对热阻增加程度间的差异比较大,间隙原子的影响因子较为显著地高于空位缺陷,这种影响间的差异也随温度的升高逐渐减小.
|
图 11 各温度下空位缺陷、间隙原子的影响因子(IF) Fig. 11 The impact factors (IF) of vacancy and interstitial at various temperatures |
对于1/κ与1/Lz的关系式(4)、(9),取模拟体系1/Lz→0的极限得体相热导率时,对应的1/κ即为体相材料的热阻(图 4、图 7中1/κ与1/Lz线性关系的对应拟合直线在1/κ轴的截距).因此有完整晶体热阻
| $ l_{d}=k \cdot \frac{1}{n}. $ | (10) |
式中k为反比关系系数. 图 11中的影响因子也可作为比较温度和两种点缺陷类型对平均自由程比值l∞/ld影响程度的参量.同温度下,间隙原子的影响因子高于空位缺陷也表明间隙原子浓度ni与声子、缺陷间散射平均自由程ld反比关系的比例系数k高于空位缺陷,间隙原子比空位缺陷更大程度引起ld减小,声子与间隙原子间有相对更大的散射几率.
4 结论1) 应用逆非平衡分子动力学(rNEMD)方法对不同温度Si晶体材料的热导率进行模拟研究,探讨该方法中主要模拟参数对结果的影响,验证方法的可靠性.根据有限尺度效应采用外推法得到体相Si晶体热导率的模拟结果与温度呈T-n的负指数关系,指数n的拟合结果与平衡法模拟及实验结果一致.
2) 点缺陷的存在引起声子与缺陷的散射,随空位缺陷和间隙原子两种点缺陷浓度的增加,各温度下Si晶体的热导率均因声子与缺陷间散射的平均自由程减小而减小.较低的点缺陷浓度使得热导率有更大程度降低,随点缺陷浓度增加,热导率下降幅度逐渐减小趋于平缓.较高缺陷浓度时温度对热导率不再具有显著影响.
3) Si晶体内存在空位缺陷和间隙原子两种点缺陷结构的相对热阻增量均在考虑的浓度范围内与缺陷浓度呈线性关系.宏观的相对热阻增量在微观上表示为材料内声子间散射与声子、缺陷间散射的平均自由程比值.相同温度下,自由程比值与点缺陷浓度间的线性关系表明点缺陷浓度与声子、缺陷间散射的平均自由程呈反比例关系.
4) 采用相对热阻增量与点缺陷浓度间线性关系的比例系数作为影响因子衡量两种点缺陷对热阻(热导率)的影响.随温度升高影响因子逐渐降低,点缺陷结构对热导率的影响减小.各温度下,声子与间隙原子比空位缺陷有更大的散射几率.间隙原子更大程度引起声子与缺陷散射平均自由程减小,使得Si晶体热导率有相对更大程度降低.
致谢
本文的数值模拟计算得到了武汉大学超级计算中心的计算支持和帮助,在此向他(她)们表示衷心的感谢.
| [1] |
HOU Chaofei, XU Ji, GE Wei, et al. Molecular dynamics simulation overcoming the finite size effects of thermal conductivity of bulk silicon and silicon nanowires[J]. Modelling and Simulation in Materialsence and Engineering, 2016, 24(4): 045005. DOI:10.1088/0965-0393/24/4/045005 |
| [2] |
LEE Yongjin, LEE Sangheon, HWANG G S. Effects of vacancy defects on thermal conductivity in crystalline silicon: A nonequilibrium molecular dynamics study[J]. Physical Review B, 2011, 83(12): 125202. DOI:10.1103/physrevb.83.125202 |
| [3] |
LEE Y H, BISWAS R, SOUKOULIS C M, et al. Molecular-dynamics simulation of thermal conductivity in amorphous silicon[J]. Physical Review B Condensed Matter, 1991, 43(8): 6573. DOI:10.1103/PhysRevB.43.6573 |
| [4] |
CAROLINA A D C, TERMENTZIDIS K, CHANTRENNE P, et al. Molecular dynamics simulations for the prediction of thermal conductivity of bulk silicon and silicon nanowires: Influence of interatomic potentials and boundary conditions[J]. Journal of Applied Physics, 2011, 110(3): 034309. DOI:10.1063/1.3615826 |
| [5] |
CAHILL D G, FORD W K, GOODSON K E, et al. Nanoscale thermal transport[J]. Journal of Applied Physics, 2003, 93(2): 793. DOI:10.1063/1.1524305 |
| [6] |
DONGRE B, WANG T, MADSEN G K H. Comparison of the Green-Kubo and homogeneous non-equilibrium molecular dynamics methods for calculating thermal conductivity[J]. Modelling Simul.Mater.Sci.Eng, 2017, 25(5): 054001. DOI:10.1088/1361-651X/aa6f57 |
| [7] |
WANG T, MADSEN G K H, HARTMAIER A. Atomistic study of the influence of lattice defects on the thermal conductivity of silicon[J]. Modelling and Simulation in Materials Science and Engineering, 2014, 22(3): 035011. DOI:10.1088/0965-0393/22/3/035011 |
| [8] |
冯晓利, 李志信, 过增元. 导热系数的分子动力学模拟研究及相关问题的探讨[J]. 工程热物理学报, 2001, 22(2): 195. FENG Xiaoli, LI Zhingxin, GUO Zengyuan. Molecular dynamics study on thermal conductivity and discussion on some related topics[J]. Journal of Engineering Thermophysics, 2001, 22(2): 195. DOI:10.3321/j.issn:0253-231X.2001.02.019 |
| [9] |
杨决宽, 陈云飞, 庄苹, 等.硅晶体热传导性能的分子动力学模拟[C]//中国工程热物理学会传热传质学学术会议. 2003: 454. YAN Juekuan, CHEN Yunfei, ZHUANG Ping, et al. Molecular dynamics study on thermal conductivity of silicon crystal[C]//Academic Conference on Heat and Mass Transfer of Chinese Society of Engineering Thermophysics. 2003: 454. http://www.cnki.com.cn/Article/CJFDTotal-GCRB200403027.htm |
| [10] |
SCHELLING P K, PHILLPOT S R, KEBLINSKI P. Comparison of atomic-level simulation methods for computing thermal conductivity[J]. Physical Review B, 2002, 65: 144306. DOI:10.1103/PhysRevB.65.144306 |
| [11] |
HOWELL P C. Comparison of molecular dynamics methods and interatomic potentials for calculating the thermal conductivity of silicon[J]. The Journal of Chemical Physics, 2012, 137: 224111. DOI:10.1063/1.4767516 |
| [12] |
SAMOLYUK G D, GOLUBOV S I, OSETSKY Y N, et al. Molecular dynamics study of influence of vacancy types defects on thermal conductivity of β -SiC[J]. Journal of Nuclear Materials, 2011, 418(1-3): 174. DOI:10.1016/j.jnucmat.2011.06.036 |
| [13] |
汪国栋.硅晶体及硅纳米线导热系数的分子动力学模拟[D].南京: 东南大学, 2006. WANG Guodong. Molecular dynamics simulation of thermal conductivity of silicon crystal and silicon namowires[D]. Nanjing: Southeast University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10286-2007030581.htm |
| [14] |
TANG Meijie, COLOMBO L, ZHU J, et al. Intrinsic point defects in crystalline silicon: Tight-binding molecular dynamics studiesof self-diffusion, interstitial-vacancy recombination, and formation volumes[J]. Physical Review B, 1997, 55(21): 14279. DOI:10.1103/physrevb.55.14279 |
| [15] |
LEUNG W K, NEEDS R J, RAJAGOPAL G, et al. Calculations of silicon self-interstitial defects[J]. Physical Review Letters, 1999, 83(12): 2351. DOI:10.1103/physrevlett.83.2351 |
| [16] |
MÜLLER-PLATHE F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity[J]. The Journal of Chemical Physics, 1997, 106(14): 6082. DOI:10.1063/1.473271 |
| [17] |
MARQUÉS L A, PELAZ L, CASTRILLO P, et al. Molecular dynamics study of the configurational and energetic properties of the silicon self-interstitial[J]. Physical Review B, 2005, 71: 085204. DOI:10.1103/PhysRevB.71.085204 |
| [18] |
BATRA I P, ABRAHAM F F, CIRACI S. Molecular dynamics study of self-interstitials in silicon[J]. Physical Review B, 1987, 35(18): 9552. DOI:10.1103/PhysRevB.35.9552 |
| [19] |
陆栋, 蒋平, 徐志中. 固体物理学[M]. 上海: 上海科学技术出版社, 2010. LU Dong, JIANG Ping, XU Zhizhong. Solid state physics[M]. Shanghai: Shanghai Scientific and TechnicalPublishers, 2010. |
| [20] |
TANG Qiheng. A molecular dynamics simulation: the effect of finite size on the thermal conductivity in a single crystal silicon[J]. Molecular Physics, 2004, 102(18): 1959. DOI:10.1080/00268970412331292777 |
| [21] |
PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1. DOI:10.1006/jcph.1995.1039 |
| [22] |
STILLINGER F H, WEBER T A. Computer simulation of local order in condensed phases of silicon[J]. Physical Review B, 1985, 31(8): 5262. DOI:10.1103/physrevb.31.5262 |
| [23] |
MAITI A, MAHAN G D, PANTELIDES S T. Dynamical simulations of nonequilibrium processes — Heat flow and the Kapitza resistance across grain boundaries[J]. Solid State Communications, 1997, 102(7): 517. DOI:10.1016/s0038-1098(97)00049-5 |
| [24] |
VOLZ S G, CHEN G. Molecular-dynamics simulation of thermal conductivity of silicon crystals[J]. Physical Review B, 2000, 61(4): 2651. DOI:10.1103/PhysRevB.61.2651 |
| [25] |
CAPINSKI W S, MARIS H J, BAUSER E, et al. Thermal conductivity of isotopically enriched Si[J]. Applied Physics Letters, 1997, 71(15): 2109. DOI:10.1063/1.119384 |
| [26] |
HOLLAND M G. Analysis of lattice thermal conductivity[J]. Physical Review, 1963, 132(6): 2461. DOI:10.1103/PhysRev.132.2461 |
| [27] |
黄坤, 谢希德. 半导体物理学[M]. 北京: 科学出版社, 2012. HUANG Kun, XIE Xide. Semiconductor physics[M]. Beijing: Science Press, 2012. |
 2019, Vol. 51
2019, Vol. 51


