2. 中南大学 机电工程学院,长沙 410083
2. 2 School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
弧齿锥齿轮由于具有承载能力大、传动比大、重合度高、传动平稳、噪声低等特点,成为航空航天、汽车、工程机械等领域中动力传递过程中的关键部件.其制造精度、安装质量、啮合性能的好坏对设备的效率、工作噪声、运转精度、使用寿命甚至安全性能都有着至关重要的影响.随着计算机技术的飞速发展,使用计算机仿真螺旋锥齿轮齿面接触分析(Tooth Contact Analysis, 简称TCA)和加载齿面接触分析(Loaded Tooth Contact Analysis, 简称LTCA)[1]已经成为一种十分重要的方法,即在齿轮产品试制之前,基于计算机软件对齿轮在载荷作用下的啮合过程进行模拟仿真分析,以获得齿轮在真实工况条件下的工作情况,对于缩短试制周期,降低试制成本,提高试制质量具有不可替代的重要意义.国内外许多学者对弧齿锥齿轮的接触分析进行了大量研究,取得了一定的研究成果.汪中厚[2]等提出一种含有齿形误差和安装误差的高精度数字化真实齿面的接触分析方法,该方法可以求解出加载条件下的齿轮传动误差, 主要考虑的是齿形误差和安装误差因素对传动误差的影响.方宗德[3-4]结合有限元法和柔度矩阵法提出了弧齿锥齿轮加载齿面接触分析理论,该方法结合了齿面几何分析与力学分析,主要研究边缘接触和有摩擦承载接触等问题对传动误差的影响.唐进元[5-7]等基于加载接触有限元分析原理, 给出弧齿锥齿轮有限元加载接触分析模型的构建方法, 研究在轻载和重载情况下轮齿的接触力、啮合刚度、传动误差变化情况, 得到载荷对传动误差的影响规律. Ding Han[8-10]等基于空间共轭曲面啮合理论, 确定出弧齿锥齿轮齿面的点矢函数, 建立了考虑误差的弧齿锥齿轮轮齿加载接触分析方法, 确定了具有误差的弧齿锥齿轮齿面接触分析的初始接触点;提出了考虑刀盘几何误差测量与补偿的齿面优化修正方法,通过不断调整齿面接触分析的初始接触点,得到了弧齿锥齿轮的良好的传动误差曲线.苏进展[11]等提出了弧齿锥齿轮四阶传动误差设计方法,通过改变接触迹线方向和参考点位置来获得四阶传动误差的表达式,但该方法只是基于齿面接触分析予以实现,没有考虑轴系结构等因素的影响.彭方进[12-13]等根据动力学原理和Lagrange乘子约束,考虑惯性载荷对螺旋锥齿轮动态啮合分析的影响,提出一种新的有限元分析模型,分析惯性载荷对螺旋锥齿轮传动误差等动态啮合特性的影响规律.刘光磊[14]等研究了安装误差对弧齿锥齿轮传动误差曲线的影响,分析了传动误差曲线对各类型安装误差变动的敏感性.樊大伟[15]等分析了齿轮设计中影响传动误差的因素,主要研究了齿距、齿轮形貌、粗糙度、印迹位置形状以及材料等因素对传动误差的影响.贺敬良[16]等研究了影响传动误差的因素,依据齿面接触分析中轮齿应力集中和边缘接触等啮合缺陷,进行了齿面修形,得到良好的传动误差曲线. Litvin F L[17-18]等通过局部综合法对弧齿锥齿轮进行加载接触分析,主要分析了齿轮啮合时传动误差的变化规律,没有考虑轴系结构以及轴变形对传动误差的影响. P.J.Gamez-Montero[19]等在齿轮轴上施加旋转副,轮齿之间施加碰撞力,并且给输入轴上添加转速,输出轴上添加扭矩的方法进行弧齿锥齿轮的动态啮合分析,最终得到了转速、啮合力以及传动误差的变化规律,但该动态啮合分析没有加入轴系结构以及轴变形的影响. Simon[20]对弧齿锥齿轮的安装位置偏差、齿形误差等方面进行研究,把理论齿面、载荷分布和传动误差与机床设定参数联系起来进行分析,得出较理想的机床设定参数,但此方法只考虑齿面误差、载荷分布、安装误差等因素对传动误差的影响. O. Vogel[21]等提出了一种基于生成过程的一般数学模型的齿面接触分析新方法,直接计算接触路径,精确确定接触路径的边界、接触点的传动误差等参数,但没有考虑复杂的轴系结构以及轴变形对接触性能的影响.上述文献主要基于调整卡参数计算出齿面结构,分析载荷大小、安装误差、制造误差等因素对弧齿锥齿轮传动误差的影响以及加载接触分析结果中的传动误差与TCA结果中的传动误差的异同与联系, 而关于齿轮轴的变形,轴的支撑刚度等轴系结构特征参数对啮合传动误差的研究较少.轴的变形、轴系结构等对弧齿锥齿轮的传动误差有着重要影响,故研究分析轴的变形、轴系结构等因素对啮合传动误差的影响是很有必要的.
本文提出并验证了一种基于通用软件工具平台,考虑轴变形、轴系结构的弧齿锥齿轮传动误差数值计算方法;应用该计算方法,分析了一对高速重载航空用弧齿锥齿轮在两种轴系支撑方案下的轮齿接触情况,得到齿面接触力、接触轨迹、轮齿变形和传动误差等实际啮合性能参数,为高性能、高精度弧齿锥齿轮的设计与制造提供了重要参考.
1 考虑轴变形的传动误差数值计算方法 1.1 考虑轴变形的传动误差数值计算原理齿轮副在某一时刻的啮合可以视为两个弹性体的接触过程,当施加载荷后,齿轮1和齿轮2相互靠近并产生接触.在接触点i处的变形协调条件为[22]
| $ u_{i}^{(1)}+u_{i}^{(2)}+\varepsilon_{i}-x_{s}-d_{i}=0. $ | (1) |
式中:ui(1)为齿轮1在i点的弹性变形;ui(2)为齿轮2在i点的弹性变形;εi 为i点初始间隙,即齿面原始误差, 其值可以取为一个较小的定值;xs为两个齿轮的刚体接近量,即齿轮副沿啮合线方向的静态传递误差;di为i点接触后的剩余间隙,其值可用有限元方法获得.具体步骤为:划分六面体网格,得到初始位置时两齿面之间的间隙;然后通过加载接触分析得到加载点对应的变形,两者求差值就是接触后的剩余间隙.
将式(1)中弹性变形ui分为宏观变形和局部变形两部分,同时考虑齿轮载荷平衡条件可以有
| $ -\lambda_{g} F_{i}-u_{c i}+x_{s}+d_{i}=\varepsilon_{i}, $ |
| $ \sum\limits_{j=1}^{n} p_{j}=P, p_{j} \geqslant 0, $ |
| $ \sum\limits_{j=1}^{n} \lambda_{i, j} p_{j}=C. $ |
式中:Fi为接触点i的载荷,其值可以由公式计算;λi, j为宏观柔度系数,表示单位载荷作用在j点处时,两轮齿在i点处产生的法向位移之和;λg为宏观变形柔度系数矩阵,将宏观变形柔度系数λi, j按行排列进行组装可以得到宏观变形柔度系数矩阵[23];uci为接触点接触变形,其值可以由公式计算;pj是作用在接触线上第j点的法向载荷;n是同一啮合位置接触线上的接触点的个数;P是齿轮传递的总载荷;C是该啮合位置轮齿的变形,其值可通过有限元方法求解.
将接触线进行分段处理,计算每一个分段的接触变形,作为相应接触点的接触变形.有限长线接触弹性接触变形的计算公式为[24]
| $ u_{c i}=\frac{F_{i}}{{\rm {\mathsf π}} E^{*} l} \ln \frac{6.59 l^{3} E^{*}\left(R_{1}+R_{2}\right)}{F_{i} R_{1} R_{2}}, $ |
| $ E^{*}=\left\{\frac{1-v_{1}^{2}}{E_{1}}+\frac{1-v_{2}^{2}}{E_{2}}\right\}^{-1}, $ |
| $ l=\sqrt[3]{\frac{6 F_{i} J_{1} R_{1}}{2 E^{*} {\rm {\mathsf π}}}}=\sqrt[3]{\frac{3 F_{i} J_{1} R_{1}}{E^{*} {\rm {\mathsf π}}}}, $ |
| $ J_{1}=\int_{0}^{{\rm {\mathsf π}} / 2} \frac{\cos ^{2} \xi}{\left(\sin ^{2} \xi+\lambda^{2} \cos ^{2} \xi\right)^{1 / 2}} \mathrm{d} \xi, $ |
| $ F_{i}=\frac{M}{r_{i} \cos \alpha_{i} \cos \beta_{i}}. $ |
式中:l为接触线的长度;R1, R2分别为两齿轮接触点的主曲率半径;E1, E2为两齿轮的材料的弹性模量;v1, v2为两齿轮材料的泊松比;M为驱动力矩;ri为点i到旋转轴的距离;αi为点i处的齿形角;βi为点i处的螺旋角.
根据上式求得静态传动误差xi后,将线长方向上的静态传递误差转化为角度方向上的传动误差为[25]
| $ x_{\theta}=\frac{x_{s}}{T(x)}, $ |
| $ T(x)=T_{0} t_{r}(x), $ |
| $ t_{r}(x)=1-t x. $ |
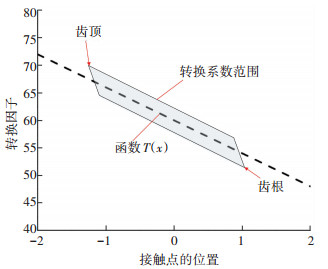
式中:如图 1所示,T(x)为角—距离转换因子;T0为转换因子幅值的大小,其值为60;t为转换因子随着x变化的程度,其值取为0.1.
|
图 1 角度-距离换算因子在齿面上的分布 Fig. 1 Distribution of angle-distance conversion factor on the tooth flank |
有限元分析方法涉及众多领域,得到广泛的应用,关于弧齿锥齿轮的有限元LTCA接触Newton-Raphson法求解逻辑流程可参考文献[26].有限元分析软件ABAQUS把分析计算过程划分为很多个载荷增量步,通过观察接触面间的相互作用状态来判断从属节点在接触对上是否开放.只有在进行多次迭代得到每个增量步的合理解后,再求解下一个增量步.所有增量步响应的总和组成了非线性分析的近似解.
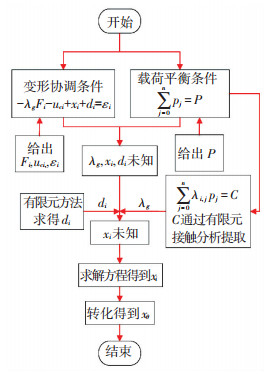
1.2 传动误差的求解流程为了求得齿轮的传动误差,基于变形协调方程与受力平衡方程,对齿轮传动误差与轴变形的关系进行了分析研究,其整体的计算流程如图 2所示.先根据给定的载荷P利用公式计算出接触点的载荷Fi和接触变形uci,然后利用有限元方法计算得到与轴变形相关的啮合位置轮齿的变形C和啮合接触后接触点之间的剩余间隙di,由轮齿变形可计算出轮齿的宏观变形柔度系数矩阵λg.最后将上述计算的参数代入变形协调方程,通过求解方程可得到齿轮线方向的静态传动误差xi,利用公式转换之后得到角度方向上的传动误差xθ.上述计算原理可借助于通用的商用软件ABAQUS、MATLAB予以实现.
|
图 2 传动误差的求解流程 Fig. 2 The process of solving the transmission error |
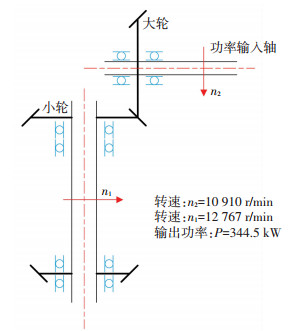
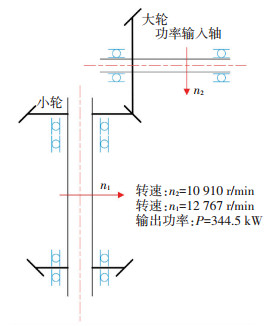
为了考虑轴变形对传动误差的影响,对两种轴系结构方案进行了分析计算.为了保证分析变量的唯一性,两种方案中工况是一样的,不同的是功率输入轴的支撑形式;图 3所示方案中的支撑形式相当于悬臂梁支撑,图 4所示方案中的支撑形式相当于简支梁支撑.其中,工况的确定主要来源于高速重载航空用弧齿锥齿轮的实际工作条件以及环境,且工况的选择需要保证弧齿锥齿轮在实际工作中不发生边缘接触、偏载等啮合缺陷,要能够得到良好的齿面接触区域、传动误差等齿面接触性能参数.
|
图 3 靠近齿轮端的支撑形式示意图(含工况) Fig. 3 Support form diagram close to the gear end (including operating conditions) |
|
图 4 远离齿轮端的支撑形式示意图(含工况) Fig. 4 Diagram of the supporting form far from the gear end (including operating conditions) |
本文以一对航空用零度弧齿锥齿轮加工为例,构建其三维几何模型和有限元分析模型,对两种轴系结构方案下的齿轮进行加载接触分析.所用的弧齿锥齿轮几何参数如表 1所示.
| 表 1 几何参数 Tab. 1 Geometric parameters |
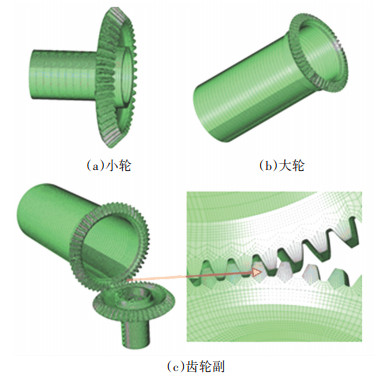
为了节省分析计算时间,提高计算效率,并且兼顾计算精度,对参与接触的齿面和相应重要部位采用较多的控制节点,网格也划分得较为密集;而在不参与接触的齿面以及对分析结果影响不大的部位则采用了较少的控制节点,相应的网格划分得也比较稀疏.最终得到的有限元模型如图 5所示.
|
图 5 弧齿锥齿轮有限元模型 Fig. 5 Spiral bevel gear finite element model |
为了更加真实地模拟齿轮副的啮合运转,设定以下的载荷以及边界条件:
1) 为提高分析计算的精度并且兼顾计算时间,分析所采用的网格类型为六面体网格(C3D8R).
2) 设定四个静态分析步,为更加接近实际啮合条件,必须保证最后两个分析步的载荷大小相同.
3) 根据齿轮的实际工况,约束两个齿轮除了绕自身轴线旋转自由度以外的其他所有自由度,并且给主动轮施加一定的转角,给从动轮施加相应的转矩载荷.
4) 将大轮的凸面(凹面)和小轮的凹面(凸面)定义为接触对,并设置切向无摩擦和法向硬接触等接触属性.
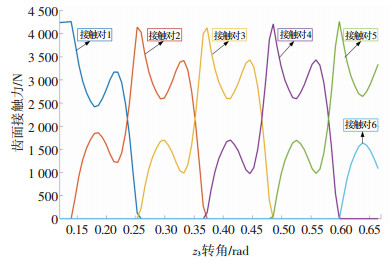
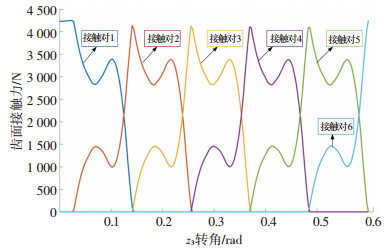
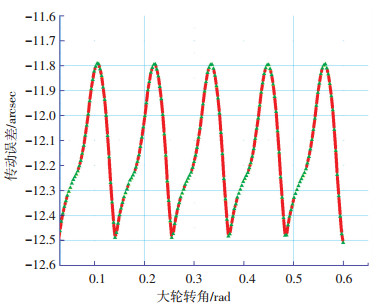
2.4 计算结果及分析基于上述有限元模型,本文就两种不同的支撑形式对弧齿锥齿轮进行了加载接触分析,得到了两种不同支撑形式下弧齿锥齿轮啮合的接触力,如图 6与图 7所示.根据分析提取出来的主从动轮转角结果,利用数值计算得到两种支撑形式下齿轮传动的传动误差曲线, 如图 8和图 9所示.
|
图 6 远离齿轮端支撑形式下的齿面接触力 Fig. 6 The tooth contact force in the form of a support away from the gear end |
|
图 7 靠近齿轮端支撑形式下的齿面接触力 Fig. 7 The tooth contact force in the form of a support near the gear end |
|
图 8 靠近齿轮端支撑形式下的齿轮传动误差 Fig. 8 Gear transmission error in the form of support near the gear end |
|
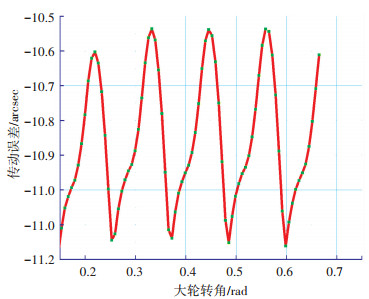
图 9 远离齿轮端支撑形式下的齿轮传动误差 Fig. 9 Gear transmission error in the form of support away from the gear end |
对比分析图 6与图 7可知:两种不同的支撑形式下接触力的总体变化趋势是一样的,在靠近齿轮一端的支撑形式下的接触力变化趋势比另外一种支撑形式下接触力的变化趋势要缓慢稳定;在最大接触力位置,远离齿轮一端的支撑形式下的接触力变化比较平缓;而在靠近齿轮一端的支撑形式下,接触力在最大峰值处变化趋势剧烈,产生了“尖顶”.原因可能是在靠近齿轮一端的支撑形式下,受齿轮轴的长度以及质量的影响,使得最大接触力变化过渡较大,而由于齿轮轴的抵抗作用,载荷对于整个齿轮系统的影响不是很明显,所以靠近齿轮一端的支撑形式下接触力整体变化趋势较缓慢稳定.在具体数值方面,在靠近齿轮端支撑形式下(图 3所示)的齿面接触力最大值为4 132.71 N,平均值为815.306 4 N;远离齿轮端支撑形式下(图 4所示)的齿面接触力最大值为4 125.29 N,平均值为735.234 8 N.
对比分析图 8与图 9可知:两种不同支撑形式下,齿轮传动误差的整体变化趋势一样,都是呈现周期性变化.在靠近齿轮端支撑形式下的最大传动误差为12.521 8 arcsec,最小传动误差为11.791 2 arcsec;在远离齿轮端支撑形式下的最大传动误差为11.161 2 arcsec,最小传动误差为10.5363 arcsec.在靠近齿轮端支撑形式下的传动误差曲线的波动幅值和整体幅值均大于远离齿轮端的支撑形式下的传动误差.原因在于:在靠近齿轮端的支撑形式下,整个齿轮轴相当于是简化的悬臂梁,由于齿轮轴受载荷作用发生变形,引起传动误差幅值波动较大,导致齿轮传动误差的增大.这也证实了在齿轮传递动力过程中,齿轮及其支撑系统产生变形都会使齿轮偏离理论位置,产生附加的传动误差这一说法.这就为降低齿轮传动误差,减少齿轮传动噪声、啮合冲击,提高齿轮传动平稳性等研究提供了参考.
2.5 本文方法计算结果与KIMoS软件计算结果对比KIMoS软件是德国KLINGELNBERG公司研制开发的螺旋锥齿轮计算应用软件,是一个模块化结构的用于所有齿制螺旋锥齿轮计算机集成设计和制造程序系统.主要用于无负载优化的齿面接触分析,干扰分析,考虑实际齿面形态,真实载荷下的齿面接触分析等,是一个快捷、使用简便、功能齐全的螺旋锥齿轮计算软件.
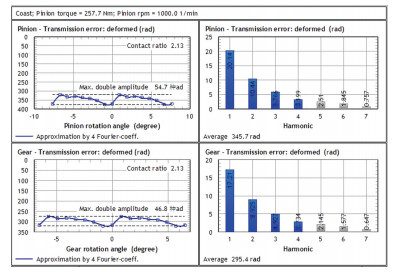
为了验证本文提出的考虑轴变形影响的传动误差的数值计算方法,利用KIMoS软件对同一对弧齿锥齿轮在远离齿轮端的支撑形式下进行了加载接触分析,得到了同等载荷,相同转速等条件下的弧齿锥齿轮的传动误差曲线和接触印痕.其中传动误差曲线如图 10所示.从图中可以看出小轮在转动角度为-7.5°~7.5°时,最大的传动误差为54.7 rad.而通过上述数值计算方法得到的相同工况条件下的弧齿锥齿轮的传动误差曲线如图 9所示,其中传动误差最大值为11.161 2 arcsec,换算为54.13 rad.比较数值计算的结果和KIMoS软件计算的结果可知,两种方法得到的传动误差曲线变化趋势一致,且最大传动误差的数值相差只有1.1%,由此可知,论文提出的数值计算方法与KIMoS软件分析计算方法有殊途同归的结果.
|
图 10 基于KIMoS计算的弧齿锥齿轮加载接触传动误差曲线 Fig. 10 The loaded transmission error curve based on the calculation of the KIMoS of spiral bevel gears |
1) 提出了一种考虑轴变形影响的弧齿锥齿轮传动误差数值计算方法,并以一对高速重载航空用弧齿锥齿轮为例,与KIMoS软件进行对比验证,结果表明论文提出的计算方法得到的结果与KIMoS软件计算结果基本一致.
2) 不同的支撑形式对齿面接触力的大小影响不大,但是由于受齿轮轴变形的影响,接触力变化的程度不一样,这就导致啮合过程中传动平稳性发生变化.
3) 根据数值计算分析结果得到轴变形对传动误差的影响较明显.在靠近齿轮一端的支撑形式下,由于齿轮轴受载荷作用发生变形,引起了附加的传动误差,导致齿轮的传动误差整体幅值变大.
| [1] |
曾韬. 螺旋锥齿轮设计与加工[M]. 哈尔滨: 哈尔滨工业大学, 1989. ZENG Tao. Spiral bevel gear design and processing[M]. Harbin: Harbin Institute of Technology, 1989. |
| [2] |
汪中厚, 李刚, 久保爱三. 基于数字化真实齿面的螺旋锥齿轮齿面接触分析[J]. 机械工程学报, 2014, 50(15): 1. WANG Zhonghou, LI Gang, KUBO Aizoh. Tooth contact analysis of spiral bevel gears based on digital real tooth surfaces[J]. Chinese Journal of Mechanical Engineering, 2014, 50(15): 1. |
| [3] |
方宗德, 邓效忠, 任东锋. 考虑边缘接触的弧齿锥齿轮承载接触分析[J]. 机械工程学报, 2002, 38(9): 69. FANG Zongde, DENG Xiaozhong, REN Dongfeng. Loaded tooth contact analysis of spiral bevel gears considering edge contact[J]. Chinese Journal of Mechanical Engineering, 2002, 38(9): 69. DOI:10.3321/j.issn:0577-6686.2002.09.015 |
| [4] |
方宗德. 齿轮轮齿承载接触分析(LTCA)的模型和方法[J]. 机械传动, 1998(2): 2. FANG Zongde. Model and method of gear tooth contact analysis (LTCA)[J]. Mechanical Transmission, 1998(2): 2. |
| [5] |
唐进元, 蒲太平. 加载螺旋锥齿轮接触轨迹变化规律的研究[J]. 机械科学与技术, 2010, 29(4): 461. TANG Jinyuan, PU Taiping. A study of contact path variation of a loaded spiral bevel gear[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(4): 461. |
| [6] |
唐进元, 蒲太平. 基于有限元法的螺旋锥齿轮啮合刚度计算[J]. 机械工程学报, 2011, 47(11): 23. TANG Jinyuan, PU Taiping. Spiral bevel gear meshing stiffness calculations based on the finite element method[J]. Chinese Journal of Mechanical Engineering, 2011, 47(11): 23. |
| [7] |
唐进元, 卢延峰, 周超. 螺旋锥齿轮齿面接触分析改进算法研究[J]. 航空动力学报, 2009, 24(1): 189. TANG Jinyuan, LU Yanfeng, ZHOU Chao. Research on improved tooth contact analysis algorithm of spiral bevel gears[J]. Journal of Aerospace Power, 2009, 24(1): 189. |
| [8] |
DING Han, TANG Jinyuan, SHAO Wen, et al. Optimal modification of tooth flank form error considering measurement and compensation of cutter geometric errors for spiral bevel and hypoid gears[J]. Mechanism & Machine Theory, 2017, 118: 14. |
| [9] |
DING Han, TANG Jinyuan, ZHONG Jue, et al. A hybrid modification approach of machine-tool setting considering high tooth contact performance in spiral bevel and hypoid gears[J]. Journal of Manufacturing Systems, 2016, 41: 228. DOI:10.1016/j.jmsy.2016.09.003 |
| [10] |
DING Han, ZHOU Yuansheng, TANG Jinyuan, et al. A novel operation approach to determine initial contact point for tooth contact analysis with errors of spiral bevel and hypoid gears[J]. Mechanism & Machine Theory, 2017, 109: 155. |
| [11] |
苏进展, 方宗德, 蔡香伟. 弧齿锥齿轮四阶传动误差的设计[J]. 华南理工大学学报(自然科学版), 2014, 42(1): 29. SU Jinzhan, FANG Zongde, CAI Xiangwei. Design of fourth-order transmission error of spiral bevel gear[J]. Journal of South China University of Technology(Natural Science Edition), 2014, 42(1): 29. DOI:10.3969/j.issn.1000-565X.2014.01.006 |
| [12] |
彭方进.基于接触动力学的螺旋锥齿轮动态啮合性能有限元分析研究[D].长沙: 中南大学, 2010 PENG Fangjin. Finite element analysis of dynamic meshing performance of spiral bevel gears based on contact dynamics[D]. Changsha: Central South University, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10533-2010188150.htm |
| [13] |
唐进元, 彭方进. 惯性载荷对螺旋锥齿轮动态啮合特性的影响研究[J]. 振动与冲击, 2011, 30(3): 161. TANG Jinyuan, PENG Fangjin. Influence of inertial load in dynamic meshing analysis of spiral bevel gears[J]. Journal of Vibration and Shock, 2011, 30(3): 161. DOI:10.3969/j.issn.1000-3835.2011.03.032 |
| [14] |
刘光磊, 张瑞庭, 赵宁, 等. 安装误差对航空弧齿锥齿轮传动误差曲线的影响分析[J]. 航空发动机, 2012, 38(2): 32. LIU Guanglei, ZHANG Ruiting, ZHAO Ning, et al. Analysis of influence of installation error on error curve of aeronautical spiral bevel gear transmission[J]. Aero Engine, 2012, 38(2): 32. DOI:10.3969/j.issn.1672-3147.2012.02.009 |
| [15] |
樊大伟, 王殿秋, 姚庆芬. 弧齿锥齿轮设计中TE值影响因素及控制方法[J]. 汽车工艺师, 2017(5): 56. FAN Dawei, WANG Dianqiu, YAO Qingfen. Influencing factors and control methods of te value in spiral bevel gear design[J]. Automobile Technologist, 2017(5): 56. DOI:10.3969/j.issn.1672-657X.2017.05.025 |
| [16] |
何渠, 贺敬良, 何畅然, 等. 弧齿锥齿轮传动仿真分析及修形优化[J]. 北京信息科技大学学报(自然科学版), 2014(6): 37. HE Qu, HE Jingliang, HE Changran, et al. Simulation analysis and modification optimization of spiral bevel gear transmission[J]. Journal of Beijing University of Information Science and Technology(Natural Science), 2014(6): 37. |
| [17] |
LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J]. Mechanism & Machine Theory, 2006, 41(1): 83. |
| [18] |
LITVIN F L, ZHANG Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears[J]. Forum, 1991, 1(2): 1. |
| [19] |
GAMEZ-MONTERO P J, CASTILL A R, KHARMASHTA M. Contact problem of a trochoidal-gear pump[J]. Interational Journal of Mechanical Sciences, 2006, 48(12): 1471. DOI:10.1016/j.ijmecsci.2006.06.013 |
| [20] |
SIMON V. Influence of tooth errors and misalignments on tooth contact in spiral bevel gears[J]. Mechanism & Machine Theory, 2008, 43(10): 1253. |
| [21] |
VOGEL O, GRIEWANK A, BÄR G. Direct gear tooth contact analysis for hypoid bevel gears[J]. Computer Methods in Applied Mechanics & Engineering, 2002, 191(36): 3965. |
| [22] |
常乐浩, 刘更, 吴立言. 齿轮综合啮合误差计算方法及对系统振动的影响[J]. 机械工程学报, 2015, 51(1): 123. CHANG Lehao, LIU Geng, WU Liyan. Determination of composite meshing errors and its influence on the vibration of gear system[J]. Chinese Journal of Mechanical Engineering, 2015, 51(1): 123. |
| [23] |
RINCON A F D, VIADERO F, IGLESIAS M, et al. A model for the study of meshing stiffness in spur gear transmissions[J]. Mechanism & Machine Theory, 2013, 61(61): 30. |
| [24] |
丁长安, 张雷, 周福章, 等. 线接触弹性接触变形的解析算法[J]. 摩擦学学报, 2001, 21(2): 135. DING Changan, ZHANG Lei, ZHOU Fuzhang, et al. Theoretical formula for calculation of line-contact elastic contact deformation[J]. Tribology, 2001, 21(2): 135. DOI:10.3321/j.issn:1004-0595.2001.02.014 |
| [25] |
MOHAMAD E N, KOMORI M, MURAKAMI H, et al. Analysis of general characteristics of transmission error of gears with convex modification of tooth flank form considering elastic deformation under load[J]. Journal of Mechanical Design, 2009, 131(6): 2751. |
| [26] |
曾攀. 有限元分析及应用(附光盘)[M]. 北京: 清华大学出版社, 2004. ZENG Pan. Finite element analysis and application (with CD)[M]. Beijing: Tsinghua University Press, 2004. |
 2019, Vol. 51
2019, Vol. 51


