轴承是空间活动部件的核心零件,在真空、温度、预紧力、转速、微重力等空间综合环境作用下,工作精度和性能逐渐退化,影响卫星姿轨控系统的稳定运行[1],因此,需要开展加速寿命试验评估,充分保证可靠性和寿命水平.
黄敦新等对上千个飞轮进行统计分析发现,轴承摩擦与磨损失效已逐渐取代电子元件成为空间活动部件失效的主要因素[2];2002年,洛阳轴承厂在开展某机械装置热平衡和热真空试验时,发现低温和高温工况下存在电机启动无效或停转现象,原因为轴承润滑失效[3];2006年,“鑫诺二号”卫星发射后太阳帆板与通讯天线未能正常展开,导致运行轨道出现偏差,损失高达20多亿元,与轴承工作异常相关[4],等等.针对轴承在轨失效问题,国内外学者开展了相关试验验证与评估工作,北京控制工程研究所开展了某卫星驱动电机轴承的载荷和温度加速试验,对相关特性进行了验证;宁峰平等研究了温度交变、载荷、转速对空间轴承稳态温度场的耦合影响特性[5];重庆大学通过设计空间轴承真空热试验装置,开展了大量温度、转速应力的加速寿命试验研究,分析了微观界面失效规律[6-7];陈仁详等开展了基于振动敏感时频特征的航天轴承寿命状态识别研究[8];阙子俊等开展了基于无迹卡尔曼滤波算法的轴承剩余寿命预测方法研究,充分利用微观失效信息,开展可靠性和寿命特征评估[9].
目前,国内外在空间轴承加速寿命试验方面,仍存在加速应力单一、加速试验机理认识不到位等问题.本论文充分考虑真空、温度、预紧力、转速、微重力综合环境下的液体润滑轴承失效模式及机理,通过建立考虑多应力综合作用机理的微观接触统一润滑模型来开展仿真分析,获得多应力加速失效规律,基于响应面方法辨识真空、温度、预紧力、转速、微重力与失效响应值之间的多应力加速模型,为加速寿命试验方案设计与评估奠定理论基础.
1 空间轴承多应力失效机理分析 1.1 真空失效模式及机理一般来说,在轨空间气压在10-11~10-3Pa之间,润滑剂粘度和摩擦系数会随气压发生变化,其失效模式及机理总结如表 1中所示[10-12].
| 表 1 真空失效模式及机理 Tab. 1 Vacuum failure mode and mechanism |
在空间环境下,受到太阳光照等影响,轴承运转的极端高低温环境和接触区表面摩擦使得界面温度不同,从而出现润滑剂粘度和摩擦系数变化,其失效模式及机理总结如表 2中所示.
| 表 2 温度失效模式及机理 Tab. 2 Temperature failure mode and mechanism |
轴承预载的大小对轴承的长寿命润滑有较大的影响,需要对预紧力进行精确测量与控制,其失效模式及机理总结如表 3中所示.
| 表 3 预紧力失效模式及机理 Tab. 3 Preload failure mode and mechanism |
轴承在不同的转速下,滚珠与内外圈之间相对接触点的运动速度不一样,导致接触界面的润滑特性发生改变,其失效模式及机理总结如表 4中所示[13].
| 表 4 转速失效模式及机理 Tab. 4 Speed failure mode and mechanism |
在微重力情况下,只有表面张力作用于润滑剂流动及热传导,从而影响供油和弹流润滑特性,其失效模式及机理总结如表 5中所示[14-15].
| 表 5 微重力失效模式及机理 Tab. 5 Microgravity failure mode and mechanism |
根据真空、温度、预紧力、转速、微重力作用下空间轴承的失效模式,推导和建立失效机理模型.
真空和温度失效机理模型主要体现在对润滑剂粘度和密度的影响,机理模型如下:
| $ \eta=\eta_{0} \mathrm{e}^{\alpha P-\beta\left(T-T_{0}\right)}, $ |
| $ \rho / \rho_{0}=\left(1+\frac{0.6 \times 10^{-9} P}{1+1.7 \times 10^{-9} P}\right) \times\left(1-\alpha_{T}\left(T-T_{0}\right)\right). $ |
式中:η为压力P和温度T下的润滑剂粘度,η0为标准大气压力和常温下的润滑剂粘度,ρ为压力P和温度T下的润滑剂密度,ρ0为标准大气压力和常温下的润滑剂密度,α为粘压系数,β为粘温系数,αT为温度膨胀系数,P为压力(即真空度),T为实际温度值,T0为常温.
转速失效机理模型主要体现在界面流体速度和滚道表面转速的边界平衡,即流体动压效应方程,如下:
| $ u=\frac{1}{2 \eta} \times \frac{\partial P}{\partial x}\left(z^{2}-z h\right)+\left(V-V_{0}\right) \frac{z}{h}+\left.V_{0}\right|_{z=h, u=V}. $ |
式中,u为流速沿膜厚方向的分布,z为膜厚方向坐标值,h为膜厚,V为轴承转速,V0为滚珠转速.
预紧力失效机理模型主要体现在油膜压力积分与预紧力的边界平衡,如下:
| $ W=\iint p \mathrm{d} x \mathrm{d} y. $ |
微重力失效机理模型主要体现在入口乏油,本文通过设置入口膜厚来等效.
2.2 微观接触统一润滑模型将上述失效机理模型与表面粗糙度一起考虑到雷诺方程中,得到考虑多应力综合作用的微观接触统一润滑模型,如下:
| $ \frac{\partial}{\partial x}\left(\frac{\rho h^{3}}{12 \eta} \frac{\partial p}{\partial x}\right)+\frac{\partial}{\partial y}\left(\frac{\rho h^{3}}{12 \eta} \frac{\partial p}{\partial y}\right)=u \frac{\partial(\rho h)}{\partial x}+\frac{\partial(\rho h)}{\partial t}. $ | (1) |
油膜厚度计算公式如下:
| $ \begin{array}{c}{h=h_{0}(t)+\frac{x^{2}}{2 R_{x}}+\frac{y^{2}}{2 R_{y}}+\nu_{e}(x, y, t)+} \\ {\quad \delta_{1}(x, y, t)+\delta_{2}(x, y, t)}.\end{array} $ | (2) |
式中,h0(t)表示两物体的刚体中心膜厚,
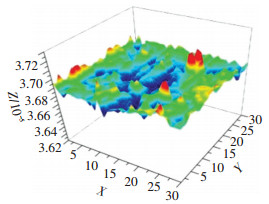
|
图 1 接触界面表面粗糙度 Fig. 1 Surface roughness of contact area |
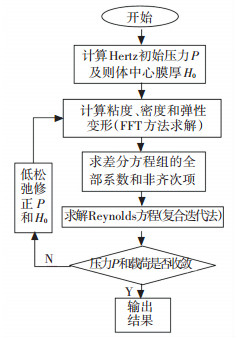
本文采用改进的牛顿-拉夫逊法对式(1)和式(2)进行数值解算,流程如图 2中所示,解算结果为微观接触界面膜厚、压力峰值、摩擦系数、最大下表面应力随应力水平及接触区尺寸变化的响应规律,从而表征液体润滑轴承的磨损和疲劳失效行为.
|
图 2 数值解算流程 Fig. 2 Numerical calculation algorithm |
在图 2中,收敛精度满足
| $ \operatorname{err}=\frac{\sum\limits_{i=0}^{400}\left|\overline{P}_{i}^{m+1}-\overline{P}_{i}^{m}\right|}{\sum\limits_{i=0}^{400}\left|\overline{P}_{i}^{m+1}\right|}<0.000 \;1. $ |
以航天用7004角接触球轴承为分析对象,其中仿真边界条件及参数如表 6中所示.
| 表 6 仿真对象及参数 Tab. 6 Simulation object and parameter |
在上述微观接触统一润滑模型的数值求解中,设计5因素5水平正交表仿真方案,其中各应力水平取值原则如下:
1) 真空(Pa):10-3、102、103、104、105.
2) 温度(℃):-20、20、40、60、80.
3) 预紧力(轴向N):35、60、80、100、120.
4) 转速(r/min):1、10、102、103、6×103.
5) 微重力(入口膜厚μm):1、2、3、4、5.
从而得到L25(55)正交试验矩阵表及仿真结果如表 7中所示.
| 表 7 正交矩阵方案及仿真结果 Tab. 7 Orthogonal matrixprogram and simulation result |
在表 7中仿真结果的基础上,深入分析真空、温度、预紧力、转速、微重力对膜厚、压力峰值、摩擦系数、最大下表面应力的影响程度,可以通过极差分析来判断.极差越大,则相应的应力类型对相应失效响应值的影响越显著,极差定义如下:
| $ R_{x}=\max \left\{K_{x}^{y}\right\}-\min \left\{K_{x}^{y}\right\}, x=1,2, \ldots, 5 ; y=1,2, \ldots, 5. $ |
式中: Rx为因素x的极差,Kxy为因素x水平y对应的失效响应值,计算得到各应力类型的极差如表 8和图 3中所示.
| 表 8 各应力类型的极差值 Tab. 8 Range value ofeach stress type |
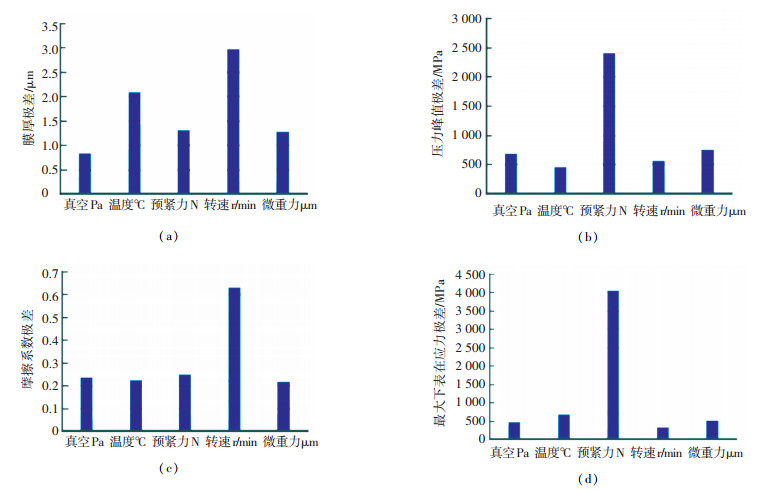
|
图 3 各应力类型对失效响应值的敏感程度 Fig. 3 Sensitive degree of failure response value with each stress type |
从表 8和图 3中可以看出,对于膜厚失效响应来说,温度和转速应力最为敏感,对于压力峰失效响应来说,预紧力最为敏感,对于摩擦系数失效响应来说,转速为最为敏感,对于最大下表面应力失效响应来说,预紧力最为敏感.可根据上述各应力类型对失效响应值的敏感程度,合理设计可靠性和寿命试验验证方案.
4 多应力加速模型建模与试验验证 4.1 二阶响应面建模基于正交矩阵方案的仿真结果,可获得膜厚、压力峰值、摩擦系数、最大下表面应力随真空、温度、预紧力、转速、微重力的响应曲面,采用二阶模型来逼近上述响应曲面方程,建模结果如下:
| $ \left\{ \begin{array}{l} {y_1} = - 0.1025 + 3.55 \times {10^{ - 6}}{x_1} - 1.7 \times {10^{ - 3}}{x_2} + 5.7 \times {10^{ - 4}}{x_3} + 2.1 \times {10^{ - 4}}{x_4}\\ \qquad + 0.09{x_5} - 2.0 \times {10^{ - 7}}{x_1}{x_5} + 1.241 \times {10^{ - 5}}{x_2}{x_3} - 2.72 \times {10^{ - 6}}{x_2}{x_4}\\ \qquad - 2.8424 \times {10^{ - 4}}{x_2}{x_5} - 2.3 \times {10^{ - 7}}{x_3}{x_4} - 3.9248 \times {10^{ - 4}}{x_3}{x_5} + 2.632 \times \\ \qquad {10^{ - 5}}{x_4}{x_5} + 2.344 \times {10^{ - 5}}x_2^2 - 8.4 \times {10^{ - 7}}x_3^2 - 9.647 \times {10^{ - 3}}x_5^2,\\ {y_2} = 716.16 - 1.65 \times {10^{ - 2}}{x_1} + 1.466{x_2} + 9.5465{x_3} + 3.97 \times {10^{ - 2}}{x_4} + \\ \qquad 68.0258{x_5} + 8.49 \times {10^{ - 5}}{x_1}{x_2} + 4.086 \times {10^{ - 5}}{x_1}{x_3} + 8.8 \times {10^{ - 4}}{x_1}{x_5} - \\ \qquad 5.036 \times {10^{ - 2}}{x_2}{x_3} - 1.085 \times {10^{ - 3}}{x_2}{x_4} + 0.262274{x_2}{x_5} + 1.625 \times {10^{ - 4}}\\ \qquad {x_3}{x_4} - 7.147 \times {10^{ - 2}}{x_3}{x_5} + 1.4178 \times {10^{ - 2}}{x_4}{x_5} + 2.55374 \times {10^{ - 2}}x_2^2 - \\ \qquad 8.9 \times {10^{ - 3}}x_3^2 - 4.58 \times {10^{ - 6}}x_4^2 - 16.5324x_5^2,\\ {y_3} = - 0.05942 - 8.25 \times {10^{ - 6}}{x_1} - 4.9692 \times {10^{ - 4}}{x_2} + 2.187 \times {10^{ - 4}}{x_3} - \\ \qquad 1.79 \times {10^{ - 5}}{x_4} + 0.0715{x_5} - 1.1 \times {10^{ - 7}}{x_1}{x_3} - 3.2 \times {10^{ - 7}}{x_1}{x_5} + 1.622\\ \qquad \times {10^{ - 5}}{x_2}{x_3} - 2.12 \times {10^{ - 4}}{x_2}{x_5} - 5.8 \times {10^{ - 7}}{x_3}{x_4} - 3.69 \times {10^{ - 4}}{x_3}{x_5} + \\ \qquad 3.53 \times {10^{ - 6}}{x_4}{x_5} + 3.94 \times {10^{ - 6}}x_2^2 + 9.6 \times {10^{ - 6}}x_3^2 - 7.62 \times {10^{ - 3}}x_5^2,\\ {y_4} = 51.203 - 1.39 \times {10^{ - 2}}{x_1} + 0.46127{x_2} + 14.588{x_3} - 5.34 \times {10^{ - 3}}{x_4} + \\ \qquad 166.765{x_5} + 6.7 \times {10^{ - 5}}{x_1}{x_2} + 1.542 \times {10^{ - 5}}{x_1}{x_3} + 2.7 \times {10^{ - 7}}{x_1}{x_4} + 7.39\\ \qquad \times {10^{ - 4}}{x_1}{x_5} - 0.04277{x_3}{x_4} + 8.76 \times {10^{ - 6}}{x_2}{x_4} + 0.4902{x_2}{x_5} + 2.67\\ \qquad \times {10^{ - 4}}{x_3}{x_4} - 0.45249{x_3}{x_5} - 4.56 \times {10^{ - 3}}{x_4}{x_5} + 0.0261x_2^2 - 0.01089x_3^2\\ \qquad - 6.03 \times {10^{ - 6}}x_4^2 - 28.837x_5^2. \end{array} \right. $ | (3) |
式中: y1为膜厚,y2为压力峰值,y3为摩擦系数,y4为最大下表面应力,x1为真空,x2为温度,x3为预紧力,x4为转速,x5为微重力.
4.2 响应面方程的显著性检验基于正交设计的响应面理论,对上述二阶响应面仿真进行显著性检验,检验统计量如下:
| $ F_{R}=\frac{S_{R}^{2} / f_{R}}{S_{E}^{2} / f_{E}}. $ |
当FR≥Fa(fR, fE)时认为响应面方程显著,各参数计算公式如下:
| $ S_{R}^{2}=S_{T}^{2}-S_{E}^{2}, $ |
| $ S_{T}^{2}=\sum\limits_{i=1}^{N}\left(y_{i}-\overline{y}\right)^{2}, $ |
| $ S_{E}^{2}=\sum\limits_{i=1}^{N}\left(\hat{y}_{i}-y_{i}\right)^{2}, $ |
| $ f_{R}=2 p+\frac{p(p-1)}{2}, $ |
| $ f_{E}=f_{T}-f_{R}, $ |
| $ f_{T}=N-1. $ |
式中: N=25为正交试验次数,p=5为影响因素数,
根据上述方法,得到Fa(fR, fE)=F0.9(20, 4)=3.84,从而得到本文二阶响应面方程检验结果如表 9中所示,表明二阶响应面方程显著.
| 表 9 二阶响应面建模检验结果 Tab. 9 Check result of second order response surface model |
为对回归系数进行显著性检验,需求出各项的偏回归平方和及σ2的估计,计算方法如下:
| $ S^{2}=S_{E}^{2} / f_{E}, $ |
| $ Q_{j}=\frac{\beta_{j}^{2}}{e^{-1}}, j=1, 2, \cdots, p, $ |
| $ e=m_{c}+2 r^{2}. $ |
式中: β表示方程系数,mc=55为全面试点数,r=7.48为正交性参数.
检验统计量如下:
| $ F_{j}=Q_{j} / S^{2}, j=1, 2, \cdots, p. $ |
如果有不显著的项,则删除该项,获得显著的参数估计结果(如式(3)所示).
4.4 试验验证案例针对上述多应力加速模型的正交矩阵仿真及响应面建模结果,选取最敏感的转速和预紧力作为加速应力,合理设计轴承加速寿命试验,试验方案及试验装置如表 10和图 4中所示.
| 表 10 步进应力加速试验方案 Tab. 10 Step stress acceleration test scheme |
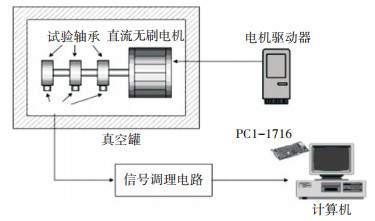
|
图 4 轴承加速试验装置 Fig. 4 Bearing acceleration test device |
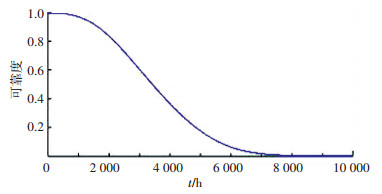
在试验过程中,通过测量摩擦力矩、温度及振动响应值来反映转速、轴向加载作用下的磨损和疲劳失效特性,试验结果表明采用本文仿真和建模结果设计的加速试验方案及数据,能很好地反映产品真实可靠性和寿命水平,如图 5和表 11所示.
|
图 5 正常条件下可靠度函数 Fig. 5 Reliability function under normal condition |
| 表 11 试验评估结果与制造商实际水平的比较 Tab. 11 Compare test result with manufacturer's actual value |
针对空间轴承多应力失效机理认识不充分、加速模型缺陷等问题,通过故障模式机理及影响分析、考虑失效机理的统一润滑模型修正、正交方案仿真分析、二阶响应面建模及试验验证,充分建立和验证了考虑真空、温度、预紧力、转速及微重力的多应力加速模型及失效规律,有效地支撑了轴承多应力加速寿命试验,主要创新点如下:
1) 深入分析了真空、温度、预紧力、转速、微重力作用下的失效机理,并将其集成到统一润滑模型中,获得了多机理竞争失效的加速模型数值解,奠定了理论基础.
2) 设计了正交仿真方案,得到了各应力作用下的疲劳和磨损失效规律,预紧力和转速是最为敏感应力,为加速试验方案设计的敏感应力类型及水平选取,提供了机理支撑.
3) 分别建立了膜厚、压力峰值、摩擦系数、最大下表面应力的多应力加速模型,通过试验验证了模型的有效性和准确性,弥补了多应力加速模型的空白.
| [1] |
张森, 石军, 王九龙. 卫星在轨失效统计分析[J]. 航天器工程, 2010, 19(4): 41. ZHANG Sen, SHI Jun, WANG Jiulong. Satelliteon-board failure statistics and analysis[J]. Spacecraft Engineering, 2010, 19(4): 41. DOI:10.3969/j.issn.1673-8748.2010.04.007 |
| [2] |
黄敦新, 白越, 黎海文, 等. 飞轮轴系润滑剂损失及寿命分析[J]. 润滑与密封, 2009, 34(9): 20. HUANG Dunxin, BAI Yue, LI Haiwen, et al. Analysis of molecular diffusion of lubricants and lubrication life of flywheel shafting[J]. Lubrication Engineering, 2009, 34(9): 20. DOI:10.3969/j.issn.0254-0150.2009.09.005 |
| [3] |
陈磊, 梁波, 田林涛. 真空环境中轴承油润滑失效原因分析[J]. 轴承, 2002(8): 31. CHEN Lei, LIANG Bo, TIAN Lintao. Failure analysis on bearing lubricated by oil in vacuum[J]. Bearing, 2002(8): 31. DOI:10.3969/j.issn.1000-3762.2002.08.011 |
| [4] |
王福亚.卫星天线双轴驱动机构健康评估与寿命预测方法研究[D].哈尔滨: 哈尔滨工业大学, 2013 WANG Fuya. Health evaluation and life rediction method study of the dual-axis drive mechanism for satellite antenna[D]. Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014002951.htm |
| [5] |
宁峰平, 姚建涛, 孙锟, 等. 多因素耦合对空间轴承热学特性的影响[J]. 浙江大学学报, 2016, 50(1): 129. NING Fengping, YAO Jiantao, SUN Kun, et al. Effect of multi-factor coupling on thermal properties of space bearing[J]. Journal of Zhejiang University, 2016, 50(1): 129. DOI:10.3785/j.issn.1008-973X.2016.01.019 |
| [6] |
赵慧.固体润滑滚动轴承加速寿命试验方法研究[D].重庆: 重庆大学机械工程学院, 2013 ZHAO Hui. Accelerated life testing method research for solid lubrication rolling bearing[D].Chongqing: College of mechanical engineering of Chongqing University, 2013 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D356095 |
| [7] |
李俊阳.空间润滑谐波减速器失效机理及其加速寿命试验方法研究[D].重庆: 重庆大学机械工程学院, 2012 LI Junyang. Failure mechanism theory and accelerated life testing method research for space lubrication harmonic drive[D].Chongqing: College of Mechanical Engineering of Chongqing University, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10611-1013007911.htm |
| [8] |
陈仁详, 陈思杨, 杨黎霞, 等. 基于振动敏感时频特征的航天轴承寿命状态识别方法[J]. 振动与冲击, 2016, 35(17): 135. CHEN Renxiang, CHEN Siyang, YANG Lixia, et al. Life state recognition method for space bearings based on sensitive time-frequency features of vibration[J]. Journal of Vibration and Shock, 2016, 35(17): 135. |
| [9] |
阙子俊, 金晓航, 孙毅. 基于UKF的轴承剩余寿命预测方法研究[J]. 仪器仪表学报, 2016, 37(9): 2037. QUE Zijun, JIN Xiaohang, SUN Yi. Remaining useful life prediction for bearings with the unscented Kalman filter-based approach[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 2037. |
| [10] |
黄志洋, 杨鹤, 彭茜, 等. 空间液体润滑剂的研究进展[J]. 石油商技, 2014(1): 20. HUANG Zhiyang, YANF He, PENG Qian, et al. Research progress of space lubricant[J]. Petroleum Business Technology, 2014(1): 20. DOI:10.3969/j.issn.1006-1479.2014.01.004 |
| [11] |
JONES W R. Lubrication for Space Applications[J]. Acad.r.p.romne Stud.cerc.mat, 2005, 91. |
| [12] |
BROWN J R, FORSTER N H. Operating temperatures in the mist lubricated rolling element bearing for gas turbines[R]. AIAA-2000-3027: 1268 https://ieeexplore.ieee.org/document/870940
|
| [13] |
SATHYAN K, HSU H Y, LEE S H, et al. Long-term lubrication of momentum wheels used in spacecrafts-An overview[J]. Tribology International, 2010, 43: 259. DOI:10.1016/j.triboint.2009.05.033 |
| [14] |
DAMIENS B, VENNER C H, CANN P M E, et al. Starved lubrication of elliptical EHD contacts[J]. Journal of Tribology, 2004, 126(1): 105. DOI:10.1115/1.1631020 |
| [15] |
CANN P M E, DAMIENS B, LUBRECHT A A. The transition between fully flooded and starved regimes in EHL[J]. Tribology International, 2004, 37(10): 859. DOI:10.1016/j.triboint.2004.05.005 |
 2019, Vol. 51
2019, Vol. 51


