2. 南京工程学院 汽车与轨道交通学院,南京 211167
2. School of Automobile & Rail Transit, Nanjing Institute of Technology, Nanjing 211167, China
运动控制作为汽车实现自主驾驶的关键环节,主要包括纵向和横向控制.纵向控制主要研究车辆的速度跟踪能力,横向控制主要研究车辆的路径跟踪能力并保证行驶稳定性[1].而环境参数的不确定性和汽车的强非线性特性,构建可处理非线性特性的运动控制方法仍然是实现汽车自主驾驶的难点[2].国内外学者针对汽车运动控制问题提出了许多方法.采用PID方法构建横向前馈及反馈控制器[3-4],解决智能车横向运动控制问题;利用最优跟踪控制理论[5-6],解决高速紧急工况的路径跟踪;利用Gauss伪谱法[7],解决汽车紧急避让的最速操纵问题;通过模糊逻辑[8]方法构建车辆横向控制分层构架,协调路径跟踪性能;采用参数空间法[9]研究横向轨迹跟踪控制策略;基于模糊逻辑的滑模控制[10]方法研究纵向速度控制策略.但上述方法仅考虑了某单一变量的跟踪控制,而针对车辆纵横向动力学间的耦合问题,李以农等[11]设计了纵横向控制“前馈+反馈”的控制策略,文献[12]构建了“上位+下位”纵横向综合控制系统,上位控制器产生期望的速度和前轮转角,下位控制器实现对期望速度和转角的跟踪控制.汽车的纵横向综合控制还应考虑汽车的侧翻稳定性,高速紧急避障主要采用紧急制动或者紧急转向两种方式避让障碍物,而在紧急避障时容易产生很大的侧向加速度,引起侧翻[13].目前针对主动防侧翻技术领域,主要采用主动制动技术[14-15]、主动转向技术[16]、主动悬架技术[17]等提高汽车抗侧翻能力.针对复杂驾驶环境中紧急避障局部路径规划问题,利用搜索多边形构造算法和势场函数可获取基于障碍的最优行进路径[18].本文通过在驾驶员方向和速度控制上引入主动制动防侧翻控制策略,实现对任意避障路径和车速的跟踪和防侧翻集成控制.
1 驾驶员—车辆模型建立匹配MEW的八自由度非线性汽车—驾驶员动力学闭环模型.
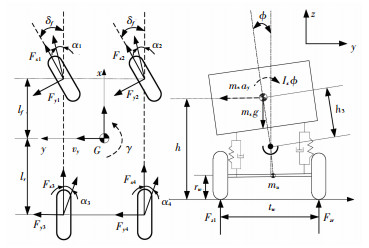
1.1 八自由度整车模型八自由度eight-degree of freedom(8-DOF)整车模型如图 1所示,该模型描述了车辆纵向运动、侧向运动、横摆运动、侧倾运动和4个车轮的旋转运动共8个自由度.忽略空气阻力,滚动阻力和车身的俯仰运动.
|
图 1 八自由度整车模型示意图 Fig. 1 8-DOF nonlinear model |
纵向运动平衡方程为
| $ m\left( {{{\dot v}_x} - {v_y}\gamma } \right) - {m_s}{h_s}\dot \gamma \varphi = \sum\limits_{i = 1}^4 {{F_{xi}}} , $ |
侧向运动平衡方程为
| $ m\left( {{{\dot v}_y} + {v_x}\gamma } \right) - {m_s}{h_s}\ddot \varphi + \left( {{l_f}{m_{uf}} - {l_r}{m_{ur}}} \right)\dot \gamma = \sum\limits_{i = 1}^4 {{F_{yi}}} , $ |
横摆运动平衡方程为
| $ \begin{array}{l} {I_z}\dot \gamma = \frac{{{t_w}}}{2}\left( {{F_{x1}} + {F_{x3}} - {F_{x2}} - {F_{x4}}} \right) + {l_f}\left( {{F_{y1}} + } \right.\\ \;\;\;\;\;\;\;\;{F_{y2}}) - {l_r}\left( {{F_{y3}} + {F_{y4}}} \right), \end{array} $ |
侧倾运动平衡方程为
| $ \begin{array}{l} {I_x}\ddot \varphi + {m_s}\left( {{{\dot v}_y} + {v_x}\gamma } \right){h_s}\cos \varphi = {m_s}g{h_s}\sin \varphi - \left( {{K_{\varphi f}} + } \right.\\ \left. {{K_{\varphi r}}} \right)\varphi - \left( {{C_{\varphi f}} + {C_{\varphi r}}} \right)\dot \varphi , \end{array} $ |
4个车轮的旋转自由度定义为
| $ {J_w}{\dot \omega _{wi}} = - {T_{{\rm{bd}}i}} - {r_w}{F_{x{\rm{w}}i}}, $ |
式中:m, ms分别为汽车的总质量和簧载质量;vx, vy分别为汽车的纵向和侧向速度;γ为汽车的横摆角速度;ϕ为汽车的侧倾角;hs是质心位置距侧倾中心的距离;δf为前轮转角;Fyi是各车轮的侧向力(i=1, 2, 3, 4);Ix, Iz是簧载质量的侧倾转动惯量和横摆转动惯量;lf, lr分别为质心位置到前后轴的距离;Kϕf, Kϕr分别为前后轴悬架的等效侧倾刚度;Cϕf, Cϕr分别为前后轴悬架的等效阻尼;Jw为车轮的转动惯量,ωwi第i个车轮的旋转角速度;Tbdi第i个车轮的制动力矩或驱动力矩;rw为车轮滚动半径.
1.2 非线性轮胎模型魔术公式magic formula(MF)是一组可以较精确描述轮胎力学特性的经验公式,其力学表达式为
| $ \begin{array}{*{20}{c}} {Y = D\sin \left( {C\arctan \left( {B\mathit{\Phi }} \right)} \right) + {S_{\rm{v}}},}\\ {\mathit{\Phi } = \left( {1 - E} \right)\left( {X + {S_{\rm{h}}}} \right) + \left( {E/B} \right)\arctan \left( {B\left( {X + {S_{\rm{h}}}} \right)} \right).} \end{array} $ |
式中:Y代表纵向轮胎力与侧向轮胎力;D是峰值因子,表示曲线的最大值;C是曲线形状因子;B为刚度因子,B=BCD/(CD);E是曲线曲率因子,表示曲线最大值附近的形状;X为车轮滑移率λ或侧偏角α;Sv为曲线的垂直方向漂移,Sh为曲线的水平方向漂移.
计算纵向轮胎力时:
| $ C = {a_{x0}},D = {a_{x1}}{F_z}^2 + {a_{x2}}{F_z},B = \frac{{{a_{x3}}{F_z}^2 + {a_{x4}}{F_z}}}{{CD{e^{{a_{x5}}{F_z}}}}}, $ |
| $ E = {a_{x6}}{F_z} + {a_{x7}}{F_z} + {a_{x8}}, $ |
| $ {\lambda _i} = \frac{{{r_w}{\omega _{wi}} - {v_x}}}{{{v_x}}}. $ |
计算侧向轮胎力时:
| $ \begin{array}{l} C = {a_{y0}},D = {a_{y1}}F_z^2 + {a_{y2}}{F_z},BCD = {a_{y3}}\sin \left( {{a_{y4}} \times } \right.\\ \arctan \left( {{a_{y5}}{F_z}} \right)),E = {a_{y6}}F_z^2 + {a_{y7}}{F_z} + {a_{y8}}, \end{array} $ |
| $ {\alpha _{1,2}} = {\delta _f} - \arctan \left( {\frac{{{v_y} + {l_f}\gamma }}{{{v_x} \pm \frac{{{t_w}}}{2}\gamma }}} \right),{\alpha _{3,4}} = \arctan \left( {\frac{{ - {v_y} + {l_r}\gamma }}{{{v_x} \pm \frac{{{t_w}}}{2}\gamma }}} \right). $ |
前后轴各车轮的垂向载荷为
| $ {F_{z1}} = \frac{{mg{l_r}}}{{2l}} - \frac{{m{a_x}h}}{{2l}} - \frac{{{a_y}}}{{{t_w}}}\left( {\frac{{{m_s}{l_r}{h_s}}}{l}} \right) - \frac{1}{{{t_w}}}\left( {{K_{\varphi f}}\varphi + {C_{\varphi f}}\dot \varphi } \right), $ |
| $ F_{z 2}=\frac{m g l_{r}}{2 l}-\frac{m a_{x} h}{2 l}+\frac{a_{y}}{t_{w}}\left(\frac{m_{s} l_{r} h_{s}}{l}\right)+\frac{1}{t_{w}}\left(K_{\varphi f} \varphi+C_{\varphi f} \dot{\varphi}\right), $ |
| $ {F_{z3}} = \frac{{mg{l_f}}}{{2l}} + \frac{{m{a_x}h}}{{2l}} - \frac{{{a_y}}}{{{t_w}}}\left( {\frac{{{m_s}{l_f}{h_s}}}{l}} \right) - \frac{1}{{{t_w}}}\left( {{K_{\varphi r}}\varphi + {C_{\varphi r}}\dot \varphi } \right) $ |
| $ F_{z 4}=\frac{m g l_{f}}{2 l}+\frac{m a_{x} h}{2 l}+\frac{a_{y}}{t_{w}}\left(\frac{m_{s} l_{f} h_{s}}{l}\right)+\frac{1}{t_{w}}\left(K_{\varphi r} \varphi+C_{\varphi_{r}} \dot{\varphi}\right). $ |
式中:l为轴距;h为质心到地面的距离;tw为轮距.
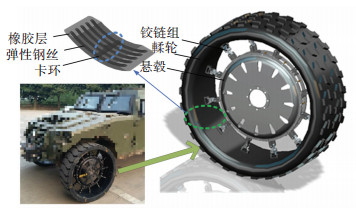
机械弹性车轮mechanical elastic wheel (MEW)是一种新型的非充气安全车轮,其结构如图 2所示,它主要由輮轮、铰链组和悬毂三大部分构成.
|
图 2 MEW结构示意图 Fig. 2 Structure of the MEW |
利用平板式轮胎力学特性试验台,对MEW样机进行力学特性试验,其基本结构如图 3所示.

|
图 3 轮胎力学特性试验台 Fig. 3 Experimental set-up for tire mechanical characteristics |
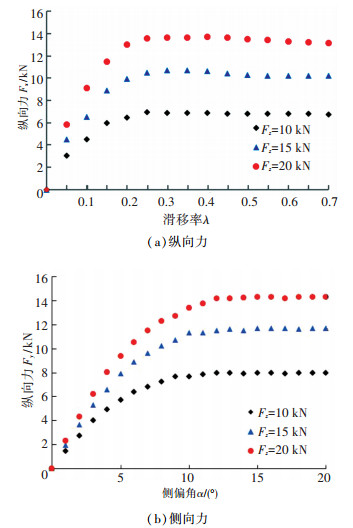
模拟路面以设定平移速度从试验台架一侧移至另一侧,MEW样机纵向与侧偏力学曲线的试验结果如图 4所示.
|
图 4 MEW力学关系曲线 Fig. 4 Tire force response of MEW |
利用遗传算法Genetic Algorithms(GAs)寻找最优解的过程首先是定义目标函数,其表达式为
| $ f\left( x \right) = \min \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left[ {{Y^{{\rm{MF}}}}\left( {P,X,{F_{zj}}} \right) - {Y^ * }\left( {X,{F_{zj}}} \right)} \right]}^2}} } . $ |
式中:P为待识别的参数,f(x)为适应的函数,m为每组样本的个数,n为试验样本组数,YMF是由MF计算得到的轮胎力,而Y*是实验测量数据.
假设为理想情况,水平方向的漂移Sh和垂直方向的漂移Sv均为0,为了提高辨识精度,缩短辨识计算时间,将MF轮胎模型分为一级辨识参数,具体为P(1)=D,P(2)=C,P(3)=B,P(4)=E,算法其他相关参数的设置为:初始种群大小为20,二级辨识参数集合为{ ax0, ax1, ax2, ax3 ax4, ax5, ax6, ax7, ax8},{ ay0, ay1, ay2, ay3 ay4, ay5, ay6, ay7, ay8},最大遗传代数为50,交叉概率为0.7,变异概率为0.1.
分别选用垂向载荷为Fz =10 kN, 15 kN和20 kN时的MEW轮胎力数据用于参数辨识.引入相对残差作为识别结果精度的评价指标为
| $ e = \sqrt {\sum {{{\left( {{Y^{{\rm{MF}}}} - {Y^ * }} \right)}^2}} /\sum {{{\left( {{Y^ * }} \right)}^2}} } \times 100\% . $ |
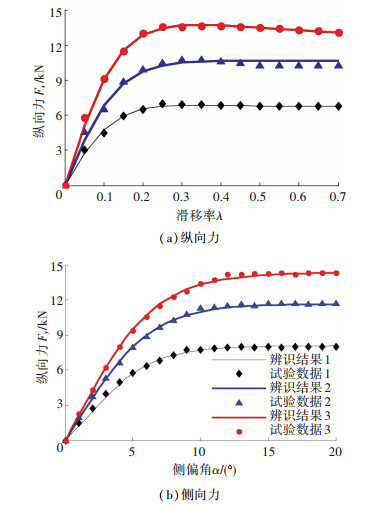
MEW轮胎模型的一级参数识别结果如表 1所示.由一级参数辨识结果拟合出的不同垂向载荷下MEW轮胎模型纵向和侧向力关系曲线如图 5所示. MEW轮胎模型的二级参数识别结果如表 2所示.
| 表 1 MEW轮胎模型一级参数识别结果 Tab. 1 Identification results of MEW first order parameters |
|
图 5 MEW力学关系拟合曲线 Fig. 5 Tire force fitting curve of MEW |
| 表 2 MEW轮胎模型二级参数识别结果 Tab. 2 Identification results of MEW second order parameters |
由图 5可知,试验数据与遗传算法计算结果基本吻合,由表 2可知,对峰值因子参数D、刚度因子参数B、曲率因子参数E辨识的精度分别为1.56%,2.33%,4.78%,辨识精度较高.纵向力的全局识别精度在5%左右,侧向力的全局识别精度在4%左右,从而验证了基于遗传算法对魔术公式轮胎模型参数辨识的有效性.
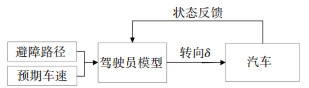
1.3 方向控制驾驶员模型本文的驾驶员模型是在已知避障路径和预期车速的前提下建立的.根据避障路径和预期车速的信息,引入车辆状态信息和位置等反馈,决策驾驶员的方向盘转角和统一加速度(制动踏板,加速踏板),方向控制驾驶员模型结构示意图如图 6、图 7所示.
|
图 6 方向控制驾驶员模型结构示意图 Fig. 6 Block diagram of the whole driver model |
|
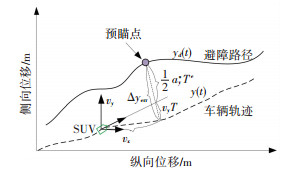
图 7 避障路径方向控制驾驶员模型 Fig. 7 Road direction control of driver model |
设车辆在t时刻的侧向位移为y(t),侧向速度为vy,预瞄时间为T的预瞄点和车辆的侧向偏差为
| $ \varDelta y_{\mathrm{err}}=y_{d}(t)-y(t). $ |
式中:yd(t)为目标轨迹侧向位置, y(t)为实际车辆轨迹侧向位置.假设车辆在当前时刻以ay*做侧向匀加速运动,可以在T时刻后到达目标轨迹,则
| $ \varDelta y_{\mathrm{err}}=y(t+T)-y(t)=v_{y} T+\frac{1}{2} a_{y}^{*} T^{2}. $ |
则
| $ a_{y}^{*}=\frac{2}{T^{2}}\left(y(t+T)-y(t)-v_{y} T\right). $ |
设车辆的侧向加速度ay对转向盘转角δ的稳态增益为Gay,达到理想侧向加速度ay*所需的方向盘转角为
| $ \delta^{*}=\frac{a_{y}^{*}}{G_{a y}}. $ |
根据2自由度线性车辆模型,汽车的侧向加速度与方向盘转角的增益和车速的关系如下:
| $ G_{a y}=\frac{v_{x}^{2}}{l I\left(1+K v_{x}^{2}\right)}. $ |
式中:
考虑驾驶员的生理限制,在Matlab中建立基于侧向加速度反馈的方向控制驾驶员模型如图 8所示.

|
图 8 加速度反馈方向控制驾驶员模型 Fig. 8 Block diagram of driver model based acceleration feedback |
图中,td为神经反应滞后时间,th为动作反应滞后时间常数,Tc为控制校正时间常数.
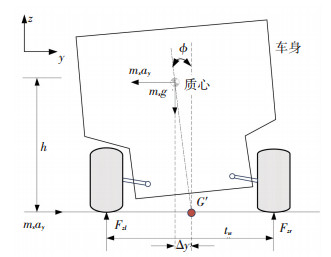
2 汽车紧急避障侧翻动态特性 2.1 汽车侧翻稳定性评价指标汽车侧倾时的简化示意图如图 9所示.
|
图 9 汽车侧翻简化模型力学分析 Fig. 9 Force analysis of vehicle rollover model |
对G′点列力矩平衡方程
| $ m_{s} a_{y} h+m_{s} g \varDelta y=\left(f_{z l}-F_{z r}\right) \frac{t_{2}}{2}, $ | (1) |
其中,Δy=h·sin φ.
汽车横向载荷转移率(LTR)为
| $ \mathrm{LTR}=\frac{F_{z r}-F_{z l}}{F_{z r}+F_{z l}}, $ | (2) |
LTR的绝对值越大则表明汽车的侧翻风险越大.将式(1)代入式(2),且ms≈m,则
| $ \mathrm{LTR}=\frac{2 h}{t_{w}}\left[\frac{a_{y}}{g}+\sin \varphi\right]. $ | (3) |
定义预测横向载荷转移率Predictive lateral-load transfer rate(PLTR)为
| $ {\rm{PLT}}{{\rm{R}}_{{t_0}}}(\varDelta t) = {\rm{LTR}}\left( {{t_0}} \right) + {\rm{L{\dot T}R}}\left( {{t_0}} \right) \cdot \varDelta t, $ | (4) |
其中Δt是预测时间,t0是当前时间.当侧倾角较小时, 假设sin ϕ≈ϕ, 将式(3)代入式(4)得
| $ \operatorname{PLTR}_{t_{0}}(\varDelta t)=\frac{2 h}{t_{w}}\left[\frac{a_{y}}{g}+\varphi\right]+\frac{2 h}{t_{w} \cdot g}\left[\dot{a}_{y}+g \cdot \dot{\varphi}\right] \cdot \varDelta t. $ | (5) |
侧向加速度的变化率
| $ \dot{a}_{y}=\frac{-C_{0}\left(a_{y}-\gamma v_{x}\right)-C_{1} \dot{\gamma}}{m v_{x}}+\frac{2 k_{f} \dot{\delta}_{f}}{m}, $ | (6) |
其中,C0=kf+kr,C1=lfkf-lrkr.
将式(6)代入式(5), PLTR的最终表达式为
| $ \operatorname{PLTR}_{t_{0}}(\varDelta t)=\frac{2 h}{t_{w}}\left[\frac{a_{y}}{g}+\varphi\right]+\\ \frac{2 h}{t_{w} g}\left[\frac{-C_{0}\left(a_{y}-\gamma v_{x}\right)-C_{1} \dot{\gamma}}{m v_{x}}+\frac{2 k_{f} \dot{\delta}_{f}}{m}+g \dot{\varphi}\right] \cdot \varDelta t. $ |
式中,Δt是预测时间且Δt=0.1 s,t0是当前时间.
2.2 汽车—驾驶员模型验证将8-DOF模型和CarSim非线性整车模型进行对比,验证8-DOF模型的准确性,以某越野车为研究对象,所取车辆的主要参数见表 3所示.
| 表 3 某越野车的主要结构参数 Tab. 3 Parameters and values for SUV vehicle model |
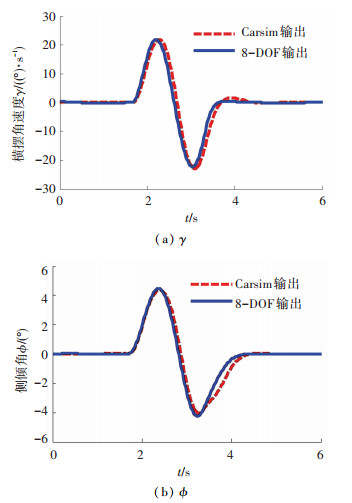
采用方向盘正弦输入,如图 10所示,仿真初始车速为60 km/h,路面附着系数为0.85,车辆的横摆和侧倾的响应对比如图 11所示.

|
图 10 方向盘正弦输入(转向传动比为20) Fig. 10 Steering wheel angle sin input test |
|
图 11 横摆与侧倾响应对比 Fig. 11 Yaw and rollover response comparison |
从图 10中可以看出,利用8-DOF仿真模型计算的横摆角速度和侧倾角与Carsim仿真结果差异较小,说明建立的8-DOF汽车仿真模型能够比较准确地描述车辆的运动.
为了验证建立的方向控制驾驶员模型的有效性,利用双移线道路(ISO3888-1999-1)作为避障路径,具体如图 12所示.

|
图 12 双移线避障试验道路模型 Fig. 12 Test path of double-lane change (DLC) maneuver |
图 12中避障道路的各段尺寸参数为
| $ s_{0}=s_{1}=s_{2}=s_{4}=2 v, s_{3}=v, s_{5}=5 v, s_{6}=3 v, $ |
| $ B=3.5 \mathrm{m}, B_{1}=1.1 L+0.25, \quad B_{2}=1.2 L+0.25, $ |
| $ B_{3}=1.3 L+0.25, $ |
其中,v为行驶速度.
驾驶员模型中,预瞄时间为一般取0.5~2.0 s, 为了获得最优的预瞄时间,综合考虑轨迹偏差E,方向盘转速
| $ J_{T}=J_{E}+J_{\delta}+J_{y}, $ |
其中
| $ J_{E}=\frac{1}{t} \int_{0}^{t}\left(\frac{E}{E^{*}}\right)^{2} \mathrm{d} t, \quad J_{\delta}=\frac{1}{t} \int_{0}^{t}\left(\frac{\dot{\delta}}{\dot{\delta}^{*}}\right)^{2} \mathrm{d} t, $ |
| $ {J_y} = \frac{1}{t}\int_0^t {{{\left( {\frac{{\ddot y}}{{{{\ddot y}^ * }}}} \right)}^2}} {\rm{d}}t, $ |
式中:

|
图 13 最优预瞄时间的综合评价指标 Fig. 13 Comprehensive evaluation of optimal preview time |
可以看出,综合评价指标JT在0.7 s处达到最小值.因此最优预瞄时间T=0.7 s.
取避障路径的中心线为要跟踪的理想道路轨迹,对道路在转角点处的突变进行三阶曲线拟合[14]后的理想道路轨迹与驾驶员模型跟踪理想避障路径的实际道路轨迹如图 14所示,其中选取的驾驶员的特性参数为:td =0.2 s,th =0.1 s. 图 15为驾驶员模型输出的方向盘转角δ.
|
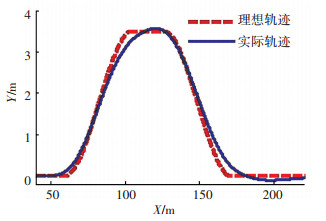
图 14 理想避障路径与实际轨迹对比(v =80 km/h) Fig. 14 Path-tracking comparison (v=80 km/h) |
|
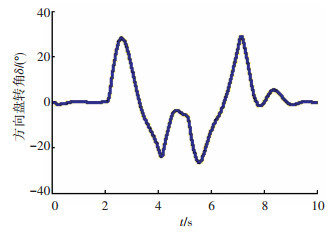
图 15 驾驶员模型输出方向盘转角 Fig. 15 Steering angle from driver model |
从图 14中可以看出,轨迹平均跟随误差约为0.1 m,瞬态最大路径跟随误差为0.35 m,跟踪效果较好,说明建立的驾驶员模型能有效的跟踪目标路径.
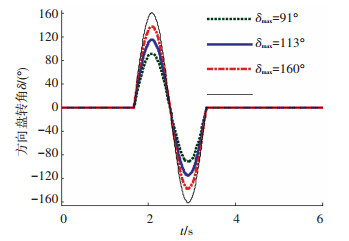
2.3 不同车速避障时的侧翻动态特性分析通过改变方向盘转角,车速,进一步分析匹配机械弹性车轮的汽车仿真模型在避障时的侧翻稳定性.首先分析不同方向盘最大转角对汽车侧翻稳定性的影响.采用方向盘正弦输入,模拟汽车进行紧急单移线避障试验,设定仿真车速为60 km/h,输入的最大方向盘转角值由91°增加到160°(图 16),其他参数不变,得到侧翻仿真结果如图 17所示.
|
图 16 方向盘正弦输入变化曲线 Fig. 16 Steering wheel angle sin input test at different δmax |
|
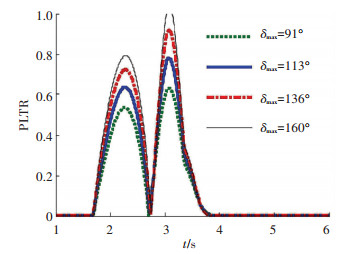
图 17 侧翻稳定性评价指标变化曲线 Fig. 17 PLTR comparison at different δmax |
可知,随着方向盘幅值的增大,各工况下PLTR的瞬态响应值变大,当方向盘转角幅值为160°, t=3.02 s时,PLTR=1,汽车此时已经发生侧翻.固定方向盘最大输入转角为113°,设定避障车速在60~120 km/h变化,PLTR的瞬态响应如图 18所示.

|
图 18 不同车速时侧翻稳定性评价指标变化曲线 Fig. 18 PLTR comparison at different vx |
从图 18中可以看出,当避障车速大于80 km/h,PLTR的瞬态值超过0.8,即汽车此时即将发生侧翻.
因此,当驾驶员在紧急避障时,要注意操纵方向盘,其转角不宜大幅度突变,车速也不宜太大.
3 高速避障方向与速度综合控制将最优车速控制与避障路径跟踪控制进行综合,形成图 19所示的避障路径与车速跟随控制的驾驶员模型.

|
图 19 方向控制和速度控制驾驶员模型 Fig. 19 Block diagram of path and speed following driver model |
车速控制和方向盘转角控制的主要耦合作用来自车速对侧向动力学特性的影响,即车辆侧向加速度增益是车速的函数,所以只需要根据车速的变化不断更新增益Gay,就可实现驾驶员速度控制和方向控制的解耦[19].
3.1 加速控制策略通过智能网联技术可以获得道路任意位置在预瞄点处的期望车速vxd,汽车纵向速度控制过程中,假设汽车以一个理想的加速度ax*行驶,同时可以在T时刻后达到期望的纵向速度,则
| $ a_{x}^{*}=\left(v_{x d}-v_{x}\right) / T. $ |
为了获取期望的纵向加速度ax*,通过PID控制决策,引入纵向加速度反馈,求出所需驱动力矩Td:
| $ T_{d}^{*}=\left(K_{p}+K_{D} s+\frac{K_{1}}{s}\right)\left(a_{x}^{*}-a_{x}\right). $ |
式中KP, KI和KD分别为PID控制的3个参数.同样速度控制要考虑驾驶员的反应滞后等生理限制.
3.2 侧翻控制策略在高速紧急避障过程中,若方向盘转角过大,或车速过大,可能造成侧翻,利用PID控制策略,建立主动制动驾驶员模型,当PLTR超过安全阀值时,主动制动车轮,控制器所需的制动力矩为
| $ T_{b}^{*}=K_{P} e_{r}+K_{I} \int_{0}^{t} e_{r} \mathrm{d} t+K_{D} \frac{\mathrm{d} e_{r}}{\mathrm{d} t}. $ |
其中, er=PLTR-PLTRs.当车速低于预期车速时,且PLTR超过安全阀值,则优先保证侧翻安全性,即优先采用制动控制策略.
3.3 仿真验证为了验证高速避障路径跟踪控制器的控制效果,在Simulink中建立方向与速度综合控制模型,设高速避让过程车辆初始纵向速度vx=80 km/h,整个避障过程车辆的侧向位移限值在10 m,最优预瞄时间取0.7 s,车辆避障距离SL取40 m.
侧翻评价指标阀值设置过小,在正常转向行驶时也会触发PLTR的预警,让侧翻控制器切换过于频繁,影响行驶效率;阀值设置过大,触发PLTR的预警时,控制器可能没有足够的时间来控制侧翻.一般侧翻的阀值设置都小于0.85,为了让侧翻控制器有足够的时间来控制侧翻,最终将侧翻的阀值设置为0.75,避障过程具体如图 20所示.

|
图 20 任意避障路径和速度跟踪示意图 Fig. 20 Visual diagram of obstacle avoidance path and speed tracking |
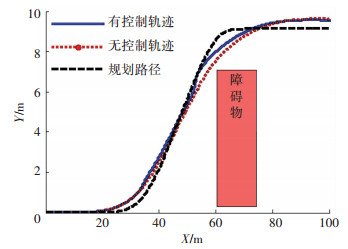
避让路径采用基于样条函数的紧急避让路径规划方法设计[20-21]. 图 21中黑色虚线为经曲线拟合后的规划避障路径,有无侧翻控制策略的避障路径跟踪效果对比,驾驶员模型方向盘转角和纵向行驶车速对比和侧翻动态特性响应对比分别如图 21~图 23所示.
|
图 21 避障路径与跟踪轨迹对比曲线 Fig. 21 Avoidance path tracking comparison |

|
图 22 驾驶员模型方向与速度控制对比 Fig. 22 Driver model comparisons |

|
图 23 有无侧翻控制的PLTR对比 Fig. 23 PLTR comparison with rollover control or not |
从图 21和图 22可知,驾驶员模型集成了侧翻控制时,方向盘转角峰值减小,且车速主动降低,避障路径跟踪效果也有一定提高.由图 23可知,有侧翻控制汽车侧翻风险明显降低,汽车的侧翻稳定性明显增强.
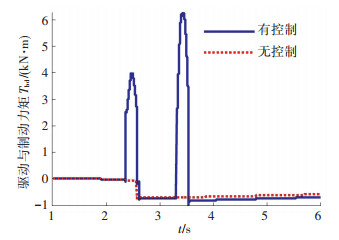
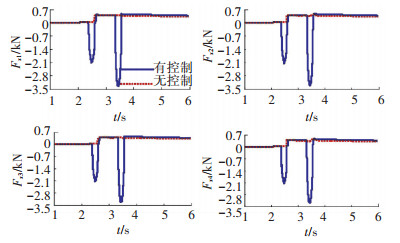
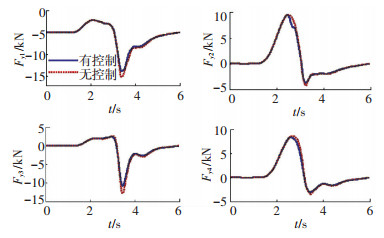
不考虑制动器与传动系统的效率和参数,驾驶员模型避障路径跟踪控制过程中所需的理想驱动与制动力矩如图 24所示. 图 25与图 26分别为有无侧翻稳定性控制时各车轮输出的纵向力与侧向力.
|
图 24 驱动与制动力矩对比 Fig. 24 Drive moment and braking moment comparison |
|
图 25 各车轮输出的纵向力对比 Fig. 25 Longitudinal force comparisons from each wheel |
|
图 26 各车轮输出的侧向力对比 Fig. 26 Lateral force comparisons from each wheel |
从图 24中可以看出,当汽车侧翻评价指标在t=2.4 s处超过0.75时,侧翻控制系统产生了最大4 000 N·m的制动力矩,主动降低车速,避免了侧翻的发生.当汽车侧翻评价指标在t=3.3 s处再次超过0.75时,侧翻控制系统产生了最大6 100 N·m的制动力矩,最终将PLTR的值控制在0.8以内,而无侧翻控制的汽车发生了侧翻失稳,侧翻评价指标PLTR的最大值超过了0.98.
4 结论1) 用遗传算法先对机械弹性车轮模型的一级参数进行辨识,然后对二级参数峰值因子参数、形状因子参数、刚度因子参数、曲率因子参数进行辨识,拟合出轮胎模型力学变化曲线,拟合曲线上的数据点与车轮台架试验的数据点基本吻合,全局识别精度均小于4%.
2) 当驾驶员在高速紧急避障时,要特别注意操纵方向盘,其转角不宜大幅度突变,车速也不宜太大.当车速超过80 km/h,且方向盘转角峰值大于120°时,汽车极易发生侧翻失稳.
3) 在转向控制驾驶员模型基础上建立速度控制驾驶员模型,并集成防侧翻控制策略,可以有效降低匹配机械弹性车轮的汽车在高速紧急避障时的侧翻风险,同时能高效完成避障路径跟踪.
| [1] |
汪瑞杰.考虑非线性与不确定性的自主无人车辆视觉系统与横向控制系统研究[D].南京: 东南大学, 2017. WANG Ruijie. Vision system and lateral control system for autonomous vehicle considering nonlinearity and uncertainty[D]. Nanjing: Southeast University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10286-1018003726.htm |
| [2] |
GUO J H, HU P, WANG R B. Nonlinear coordinated steering and braking control of vision-based autonomous vehicles in emergency obstacle avoidance[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3230. DOI:10.1109/TITS.2016.2544791 |
| [3] |
HAN G, FU W, WANG W, et al. The lateral tracking control for the intelligent vehicle based on adaptive PID neural network[J]. Sensors, 2017, 17(6): 1244. DOI:10.3390/s17061244 |
| [4] |
赵熙俊, 陈慧岩. 智能车辆路径跟踪横向控制方法的研究[J]. 汽车工程, 2011, 33(5): 382. ZHAO Xijun, CHEN Huiyan. A study on lateral control method for the path tracking of intelligent vehicles[J]. Automotive Engineering, 2011, 33(5): 382. |
| [5] |
FEKIH A, SEELEM S. Effective fault-tolerant control paradigm for path tracking in autonomous vehicles[J]. Systems Science & Control Engineering, 2015, 3(1): 177. |
| [6] |
邱笑寅.高速紧急避让汽车操纵逆动力学的建模与仿真[D].南京: 南京航空航天大学, 2012. QIU Xiaoyin. Vehicle handling inverse dynamics modeling and simulation while encountering an emergency collision avoidance[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041252.htm |
| [7] |
LIU Yingjie, JIANG Junsheng. Optimum path-tracking control for inverse problem of vehicle handling dynamics[J]. Journal of Mechanical Science and Technology, 2016, 30(8): 3433. DOI:10.1007/s12206-016-0701-9 |
| [8] |
PEREZ J, MILANES V, ONIEVA E. Cascadearchitecture for lateral control in autonomous vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(1): 73. DOI:10.1109/TITS.2010.2060722 |
| [9] |
RATHGEBER C, WINKLER F, ODENTHAL D, et al. Lateral trajectory tracking control for autonomous vehicles[C]// Control Conference. Portland, OR: IEEE, 2014: 1024 https://ieeexplore.ieee.org/document/6862324
|
| [10] |
HU P, GUO J, LI L, et al. A robust longitudinal sliding-mode controller design for autonomous ground vehicle based on fuzzy logic[J]. International Journal of Vehicle Autonomous Systems, 2013, 11(4): 368. DOI:10.1504/IJVAS.2013.056619 |
| [11] |
冀杰, 李以农, 郑玲, 等. 车辆自动驾驶系统纵向和横向运动综合控制[J]. 中国公路学报, 2010, 23(5): 120. JI Jie, LI Yinong, ZHENG Lin, et al. Integrated control of longitudinal and lateral motion for autonomous vehicle driving system[J]. Chin J Highway and Transp, 2010, 23(5): 120. |
| [12] |
BAE I, MOON J, CHA J, et al. Integrated lateral and longitudinal control system forautonomous vehicles[C]// IEEE International Conference on Intelligent Transportation Systems. Qingdao: IEEE, 2014: 406 https://ieeexplore.ieee.org/document/6957724
|
| [13] |
ROSOLIA U, BRUYNE S D, ALLEYNE A G. Autonomous vehicle control: a nonconvex approach for obstacle avoidance[J]. IEEE Transactions on Control Systems Technology, 2017, 25(2): 469. DOI:10.1109/TCST.2016.2569468 |
| [14] |
YANG X J. Improvements in vehicle handling and stability by a novel wheel slip coordination control scheme[J]. International Journal of Vehicle Design, 2013, 62(2/3/4): 206. DOI:10.1504/IJVD.2013.052702 |
| [15] |
LI L, LU Y S, WANG R R, et al. A 3-Dimentional dynamics control framework of vehicle lateral stability and rollover prevention via active braking with MPC[J]. IEEE Transactions on Industrial Electronics, 2016, 99(6): 1. |
| [16] |
WU J, CHENG S, LIU B, et al. A human-machine-cooperative-driving controller based on AFS and DYC for vehicle dynamic stability[J]. Energies, 2017, 10(11): 1737. DOI:10.3390/en10111737 |
| [17] |
LI Haiqing, ZHAO Youqun, LIN Fen, et al. Nonlinear dynamics modeling and rollover control of an off-road vehicle with mechanical elastic wheel[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2018, 40(2): 1. |
| [18] |
周自维, 李长乐, 赵杰, 等. 复杂局部地形中的实时路径规划算法设计[J]. 哈尔滨工业大学学报, 2014, 46(8): 65. ZHOU Ziwei, LI Changle, ZHAO Jie, et al. A real time path planning algorithm based on local complicated environment[J]. Journal of Harbin Institute of Technology, 2014, 46(8): 65. |
| [19] |
丁海涛, 郭孔辉, 李飞, 等. 基于加速度反馈的任意道路和车速跟随控制驾驶员模型[J]. 机械工程学报, 2010, 46(10): 116. DING Haitao, GUO Konghui, LI Fei, et al. Arbitrary path and speed following driver model based on vehicle acceleration feedback[J]. Journal of Mechanical Engineering, 2010, 46(10): 116. |
| [20] |
王健.汽车在两种转向工况下的路径规划与路径跟踪研究[D].南京: 南京航空航天大学, 2015. WANG Jian. Research on path planning and path tracking for automobile in two steering conditions[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10287-1016751995.htm |
| [21] |
ZHAO J, GUO Y, DUAN X. Dynamic path planning of emergency vehicles based on travel time prediction[J]. Journal of Advanced Transportation, 2017(11-12): 1. |
 2019, Vol. 51
2019, Vol. 51


