液压阀作为液压系统中的控制元件,通过控制液压系统中流体的流向、压力及流量,从而使液压执行元件及其驱动的工作机构获得所需的运动方向、运动速度(转速)及推力(转矩)等,达到传动及控制等需求,因此液压阀在液压系统中的作用尤为重要[1].由于液压锥阀具有线性密封、无死区、灵敏性好、通流能力强、加工成本低等优点,故较好地满足了液压阀未来的发展需求.由于锥阀内流体介质的流动情况十分复杂,会产生漩涡、回流、高急流等流动状态.当油液流经锥阀阀口位置时,流速增高,压力降低,析出气泡,从而形成气泡与流体的“气-液两相”运动.大量的混沌气穴不仅会影响阀芯稳定性,也会诱发噪声,并且长时间的气穴堆积会在阀芯表面形成气蚀,对部件造成永久性的破坏,影响精密程度,引起锥阀失效,致使无法正常工作.综上所述,对液压锥阀存在的气穴及噪声问题的研究对液压阀甚至液压系统的性能提升及延长使用寿命具有重要的意义[2-4].
国内外研究者针对液压阀内的气穴现象等问题进行了大量开拓性的研究工作. Oshima[5]对锥阀气穴噪声问题进行了较为深入的研究,分析了气穴发生时的临界条件,及气穴与压力场和速度场三者之间的关系. Inoue F[6]等人使用二维模型和湍流场来研究阀口处的空化、漩祸及边界层分离情况,结合边界层厚度和流量系数分析了气穴发生的判决依据. Ueno H[7]等人运用有限元分析法进行气穴现象的仿真研究,指出内流场的气穴是噪声的主要来源之一,并通过优化阀的结构降低了噪声. Bernad S[8]等人对锥阀模型进行了数值模拟研究,分别采用了单相流和液-气双相流两种流场形式,并通过分析和比较仿真结果,给出了流场内发生气穴的区域及明显产生漩涡的位置. Chen Q[9]等基于流体计算动力学理论,分别选取RNG k-ε湍流模型和标准k-ε湍流摸型进行了锥阀的空化仿真研究. Dayun YI[10]指出液压锥阀产生啸叫噪声的条件是流体不稳定产生的周期性压力扰动信号的频率与阀腔声学共振频率接近.高殿荣等人[11]针对外流式液压锥阀,从二维模型到三维模型依次深入探究,巧妙地结合Galekin有限元计算法和DPIV手段进行现象图像验证,给出了速度变化规律和流线云图,以及阀口与阀芯角度之间的关系.王京涛[12]等人提出采用二级节流同时以过度圆弧的结构代替液压锥阀阀芯及阀座等关键部位的直角结构,可以有效地减小锥阀过流间隙的前后压差,从而可以有效降低锥阀阀口发生气穴的可能性,并可以减小振动、噪声及能量损失.谭剑波[13]针对液压锥阀喷流的特点对阀流场进行了数值计算和模拟,分析了关键几何尺寸对锥阀的气穴现象的影响规律.张健[14]研究锥形节流阀气穴问题,通过仿真和试验研究分析5种不同节流槽阀芯的压力特性及气穴气泡发生的主要部位, 研究分析了气穴发生时所伴随的噪声及气泡发光现象,对工业用锥形节流阀的设计具有一定的参考意义.易达云[15]利用试验与仿真等手段揭示了振荡流场中空泡溃灭导致噪声增强的机制,指出锥阀振动破坏了回流低压区中固定型空化结构,使气核通过回流低压区时发展成空泡的事件增加,加剧了空化程度,基于锥阀中空化现象产生机理给出了低空化噪声锥阀的优化方案.
目前,在国内外学者关于锥阀相关问题的研究中很少有考虑阀芯发生径向偏移的情况,但实际上,液压系统在运行时,存在液压油脉动、系统振动、气穴等问题,流体介质作用在阀芯上的径向力无法达到完全相互抵消的理想状态[16-17],因此阀芯在径向上存在偏移现象.针对此现象,本文通过数值模拟计算出径向偏移量的大小、方向,结合阀芯半锥角、开口度、背压等影响因素,在考虑阀芯径向偏移的情况下,基于FLUENT软件对锥阀的气穴现象进行了液-气两相流的仿真,获得锥阀内流场的气穴分布及变化规律,并通过相对应的实验研究同仿真结果进行对比,验证其正确性,对液压锥阀的性能研究具有一定的指导意义.
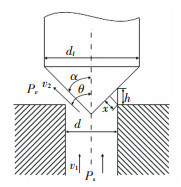
1 液压锥阀阀芯受力分析 1.1 锥阀阀口流量与液动力计算本文选取的锥阀类型为全锥阀芯和直角阀座,流向选择外流式.当阀口打开至行程内的任意开口度x时,绘制阀口剖切面的几何模型如图 1所示.
|
图 1 锥阀阀口过流断面图 Fig. 1 Cross section diagram of cone valve port |
如图 1所示,在锥阀阀芯移动的行程内,过流断面是一个圆台的侧面,其面积随着开口度大小而改变.它的基圆是阀座的进油口,母线是阀座的直角顶点到阀芯锥面的垂线,即开口度.因此得到阀口通流面积公式为
| $ A_{0}=\pi d h\left[1-\frac{\sin (2 \alpha)}{2 d} h\right] \sin \alpha. $ | (1) |
式中:d为入口直径(mm),α为阀芯半锥角(°),h为阀芯移动距离(mm).
因为锥阀结构尺寸精小,阀芯开口度也较小,故采用小孔流量方程作为计算阀口通流量的方程.其流量方程表达式为
| $ Q=C_{d} A_{0} \sqrt{\frac{2\left(p_{s}-p_{v}\right)}{\rho}}. $ | (2) |
式中:ps为入口压力(MPa),pv为出口压力(MPa),ρ为流体密度(kg/m3),Cd为流量系数,经验取值为0.8.
锥阀稳态液动力表达式为
| $ F_{w}=-2 C_{d} C_{v} A_{0} \varDelta p \cos \alpha. $ | (3) |
由于在理论计算公式的推导建立的过程中,存在适当的简化和忽略项,如液体流经阀口时的射流角度使用阀芯半锥角代替,流体入口速度忽略不计, 因此理论计算公式也存在一定的偏差.为了探究锥阀液动力对阀芯的影响,本文采用CFD方法对锥阀内流场液动力进行模拟计算.
1.2 锥阀阀芯径向力计算在研究流体对阀芯产生的作用力时,往往重点考虑的是针对轴向的作用力,大多数的研究认为阀芯受到的径向力可以达到一种相互抵消[18-19]的理想状态.然而流体的湍流状态十分复杂,没有固定的形式和路径.而锥阀中开口面积很小,液压油流过阀口时存在高急流、漩涡流等流动状态, 因此在锥阀力学特性的研究中对阀芯受到的径向力的探究必不可少.
目前在国内外的研究中,有关径向偏移的理论研究较少,在关于径向偏移的阀芯径向受力研究中,日本学者Maeda[20]提出了一个重要的无量纲参数:R*(阀座比),即阀座水平边缘处的直径与阀芯锥尖位置阀座的直径的比值.如图 2所示的阀芯径向偏移结构图为本文研究对象,其中R*为1.通过一维雷诺方程推导,并代入流量方程,得到此结构的稳态流动下偏心阀锥所受到的径向力公式为

|
图 2 阀芯径向偏移结构图 Fig. 2 Radial offset diagram of spool |
| $ F=-\pi r p_{s}\left(R^{*} C_{d}\right)^{2} x_{d} \cot \alpha. $ | (4) |
式中:r为锥阀入口半径(mm),ps为锥阀入口压力(MPa),R*为阀座比,Cd为流量系数,xd为阀芯径向偏心位移(mm),α为阀芯半锥角(°).
实际中,锥阀阀芯的受力情况比较复杂,一般存在液动力、剪切力、时变力等影响,很难得到精确的理论计算值.本文通过采用CFD技术对阀芯受到的流体作用力情况进行解析,在基于CFD计算得到轴向稳态液动力的情况下,根据式(4)近似求得阀芯径向偏移量的大小,为后续两相流仿真提供了理论基础.
1.3 锥阀内流场数值模拟在液压阀流场的研究中,CFD技术在流体工程中有着越来越广泛的应用[21-22].本文使用流场仿真软件FLUENT对锥阀内流场进行了数值模拟.选取半锥角为45°的阀芯结构锥阀,建立了7个不同开口度下的内部流场模型.其中0.2 mm、0.6 mm、1.0 mm、1.4 mm下的模型如图 3所示.

|
图 3 不同开度下锥阀内流场模型 Fig. 3 Internal flow field model of cone valve under different opening |
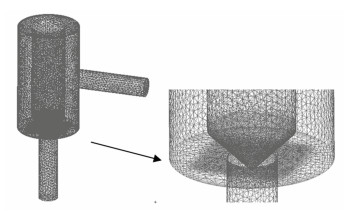
将建立好的三维模型导入到ICEM-CFD中进行网格模型的划分.对尖角处、流速高和压力梯度大的区域进行网格加密处理从而使计算结果更加精确,同时为了模拟近壁面流场,又加入了边界层网格来模拟近壁面流场,边界层网格的初始层厚度为0.1mm,增长率为0.2,层数为5层.划分完成的锥阀内流场网格模型如图 4所示,网格质量检查良好,符合计算要求.将划分好的网格模型导入到FLUENT中进行仿真模拟, 选择稳态的湍流模型,在高精度的Coupled耦合求解器下进行模拟计算.
|
图 4 锥阀内流场网格模型 Fig. 4 Mesh model of internal flow field of cone valve |
设置入口压力为5 MPa,出口压力为0 MPa,通过初始化,进行迭代计算.通过残差曲线图观察计算收敛情况. 图 5所示的残差曲线,横坐标表示数值计算的迭代数,纵坐标为残差值.
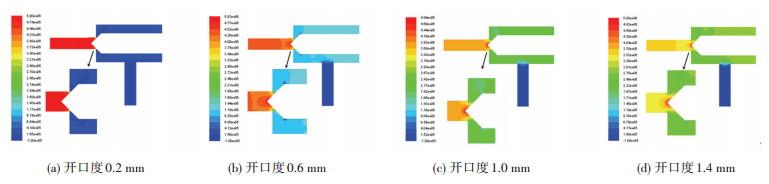
由图 5可知,仿真计算结果收敛性良好.由于液压锥阀的内流场模型是沿轴面对称的结构,为了更清晰地展示阀口区域的压力分布情况,通过FLUENT的后处理选取0.2 mm、0.6 mm、1.0 mm、1.4 mm开口度下的对称截面的压力云图及阀口位置放大图作展示,如图 6所示.

|
图 5 残差收敛曲线 Fig. 5 Residual convergence curve |
|
图 6 不同开度下锥阀内流场压力分布 Fig. 6 Pressure distribution in the inner flow field of the cone valve under different opening |
由图 6可以看出,随着开口度的增大,内流场的压力分布变得越来丰富.具体的明显变化为:1)液压油入口的近阀芯域逐渐形成低压;2)开口度位置,压力梯度层次分布较多;3)阀芯锥面与圆柱面的转折处的整个圆周呈现出极小压,阀腔内压力云图成云状分布在阀芯两侧,其形式不对称.
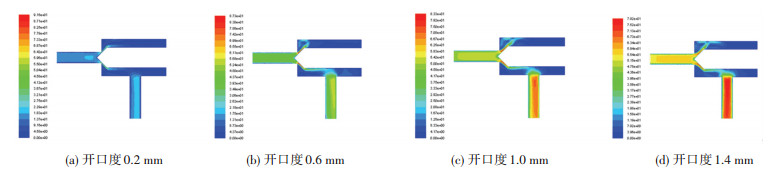
为了进一步观察内流场的分布情况,结合对应开口度下流场速度变化云图 7进行分析.
|
图 7 不同开口度下锥阀内流场速度分布 Fig. 7 Velocity distribution of inner flow field in cone valve with different opening |
根据图 7所示流场分布.可看出随着开口度的增大,形成的漩涡流现象更明显,并且阀芯两侧的云状流速形态不同,因此随阀芯的作用力分布也不同.将阀芯两侧有效面积上的流体压强进行积分得到阀芯两侧的径向作用力如表 1所示.其中表 1所述的上锥面为远离出口一侧的阀芯表面,下锥面为靠近出口一侧的阀芯表面.
由表 1可知,在开口度较小时,阀芯两侧受到的径向受力基本相同,随着开口度的增大,压力差值逐渐变大,约在0.4 mm的开口度以后,阀芯下锥面受到的径向力比上锥面大的压力值基本维持在9~11 N左右.选取稳态下开口度大于等于0.6 mm时的阀芯两侧径向力差值代入到径向力的公式(4)中,计算得到径向偏移量为0.4 mm左右,偏移方向为向下锥面一侧偏移.将其引用在后续的锥阀气穴的仿真研究中,作为参考值.
| 表 1 随开口度变化的阀芯表面受力 Tab. 1 Radial force data with the change of the opening |
根据上文提出阀芯存在径向偏移的现象,结合阀芯半锥角、背压、开口度等因素,基于FLUENT软件对锥阀内流场进行气-液两相流仿真.在仿真研究中,特别选取了Mixture多相流模型、Zwart-Gerber-Belamri气穴模型及声学模型.液相选用了32#抗磨液压油,密度为870 kg/m3,粘度2.784×10-2 Pa·s;气相的密度为1.225 kg/m3,粘度1.26×10-6 Pa·s;饱和蒸气压1 000 Pa.声速2 730 m/s,远场密度1.18 kg/m3.入口边界选择压力入口,出口边界设置压力出口.
2.1 径向偏移对锥阀气穴的影响由于振动、脉动等不稳定因素影响,液压锥阀在工作时径向偏移量会与理论计算值存在一定偏差,故结合计算结果选取0 mm、0.2 mm、0.4 mm、0.6 mm作为径向偏移的变量值,开口度0.6 mm,阀芯半锥角45°,背压0.6 MPa.依次在入口压力1 MPa、2 MPa、3 MPa、4 MPa、5 MPa下进行仿真.
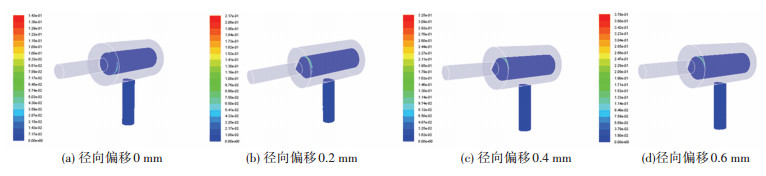
为了直观展示阀口以及阀芯表面气穴分布情况,在后处理中将其他部分流域设置成透明色.其中入口压力4 MPa工况下(下同)的气穴现象如图 8所示.在阀芯未发生径向偏移时,气穴的主要析出位置是在阀芯圆锥与圆柱过渡处的整个圆周位置,且气穴分布比较均匀.随着径向偏移量的增大,气穴的分布位置发生变化,逐步向上锥面的一侧区域转移.当径向偏移量达到0.4 mm时,下锥面的一侧已经基本不见气穴发生,但上锥面的一侧气穴强度越来越强.
|
图 8 不同径向偏移下气穴分布 Fig. 8 Distribution of cavitation under different radial migration |
将仿真结果中的最大气相体积分数绘制曲线,如图 9所示,气穴的强度随着入口压力的增大而增大.在偏移量为0 mm时,入口压力2 MPa以后开始析出气穴;当径向偏移大于0.4 mm时,在入口压力为2 MPa时,气穴早已析出.相同工况下,气穴强度随着径向偏移量的增大而增大.

|
图 9 最大气相体积分数变化曲线 Fig. 9 Maximum vapor volume fraction curve |
综上径向偏移对气穴影响分析, 在阀芯径向偏移量0 mm时,气穴分布在阀芯的圆锥与圆柱的转折位置均匀分布.随着径向偏移量的增加,气穴主要聚集在上锥面一侧,下锥面一侧几乎不见气穴,且气穴强度随偏移量的增大而增强.故阀芯发生径向偏移,会引起气穴聚集,导致局部高度气蚀.
2.2 阀芯半锥角对锥阀气穴现象的影响选取半锥角度为35°、40°、45°、50°的4种阀芯.设置径向偏移量为0.4 mm,开口度0.6 mm,背压0.6 MPa.依次在入口压力1 MPa、2 MPa、3 MPa、4 MPa、5 MPa下进行仿真.
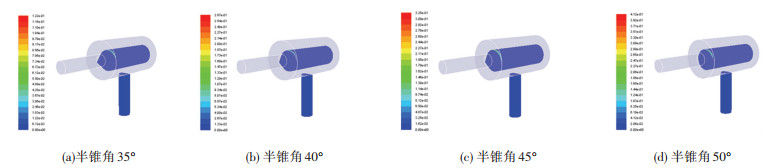
经过后处理得到气穴分布云图如图 10所示,随着半锥角度的增大,气穴现象越明显,然而半锥角度为40°和45°的阀芯下气团的强度相近,半锥角50°时气穴分布更集中,更明显.气穴分布在阀芯的上锥面一侧,半锥角度对气穴的分布影响不大.
|
图 10 不同半锥角下气穴分布云图 Fig. 10 Distribution of cavitation and pressure under different half cone angle |
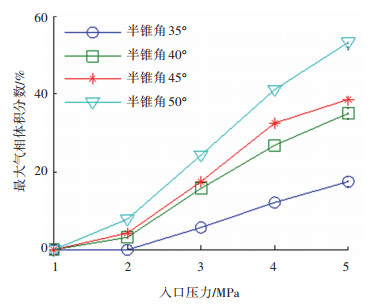
由仿真结果得出的不同半锥角度下的气相变化的曲线如图 11所示.在相同工况下,半锥角度变大,则气穴析出的体积占比变大;但在40°和45°角时气穴的最大气相体积分数比较相近;在半锥角50°时气穴现象明显比其他3种角度都强烈,局部最大气相体积分数占比最高达到53.5%.随着半锥角度增大,气穴现象越强烈,40°和45°时气穴强度相近,变化稳定.
|
图 11 最大气相体积分数变化曲线 Fig. 11 Maximum vapor volume fraction curve |
综上所述,通过分析半锥角对气穴的影响,可以发现,随着半锥角增大,气穴强度增加,在40°和45°角时气穴强度相近,在50°角时气穴强度强烈, 但在相同开口度下,半锥角小的锥阀通流量小.故综合通流能力、气穴强度衡量,半锥角为45°时是一个较优的阀芯半锥角度.
2.3 开口度对锥阀气穴现象的影响选取开口度为0.4 mm、0.6 mm、0.8 mm、1.0 mm, 设置径向偏移量0.4 mm,背压0.6 MPa,半锥角45°.依次在入口压力1 MPa、2 MPa、3 MPa、4 MPa、5 MPa下进行仿真.
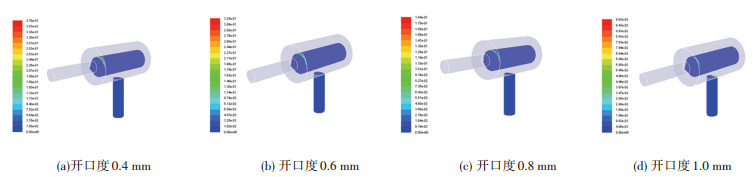
不同开口度下气穴分布如图 12所示.各个开口度下,气穴分布均聚集在上锥面一侧,但气穴强度明显减小;当开口度为1.0 mm时,如图 12(d)所示,阀芯表面气穴云团明显减弱,但出口位置出现了明显气穴云团.
|
图 12 不同开口度下气穴分布 Fig. 12 Distribution of cavitation under different opening |
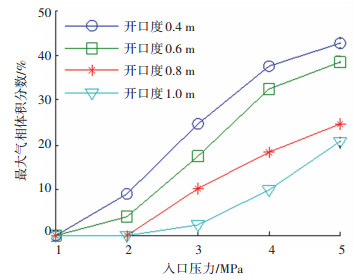
将仿真结果绘制相关最大气相占比曲线,如图 13所示.在相同入口压力下,随着开度的增加,气穴的产生逐渐被抑制;在开口度为0.4 mm和0.6 mm时,最大气穴体积分数变化趋势相同,然后随开口度增大,最大气相体积分数增加速度越来越快.
|
图 13 最大气相体积分数变化曲线 Fig. 13 Maximum vapor volume fraction curve |
综上所述,通过分析开口度对气穴的影响,可以发现,增加开口度可以抑制阀口流场的气穴强度,但是当开口度过大时,也会引起出油口位置流场气穴的析出.
2.4 背压对锥阀气穴现象的影响选取背压值为0 MPa、0.2 MPa、0.4 MPa、0.6 MPa, 设置径向偏移量0.4 mm,开口度0.6 mm,半锥角45°.依次在入口压力1 MPa、2 MPa、3 MPa、4 MPa、5 MPa下进行仿真.
不同背压下的气穴分布如图 14所示.在无背压时,气穴现象非常明显,在阀芯表面形成了强烈的气团,甚至延续至出口位置出现深色的气团,如图 14(a)所示.当背压逐渐增加时,气穴强度逐渐减弱;阀芯上锥面及出口位置的气穴现象皆逐渐减弱;在背压0.6 MPa时出口位置的气穴已完全被抑制.

|
图 14 不同背压下气穴分布云图 Fig. 14 Distribution of cavitation under different backpressure |
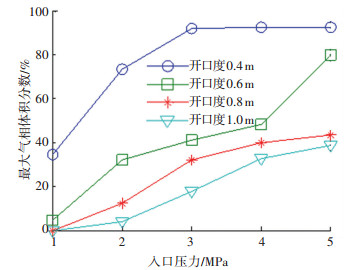
根据仿真结果,绘制了不同背压下的气相变化曲线如图 15所示.可以发现,在无背压时,气穴强度特别强烈,在入口压力3 MPa时最大气相占比高达92.1%,在4 MPa时,占比为92.4%,在5 MPa时,占比为92.6%;随着背压的增大,气穴强度明显减弱.当背压增加到0.6 MPa时,随着入口压力的增大,气穴强度增加速度非常缓慢.
|
图 15 最大气相体积分数变化曲线 Fig. 15 Maximum vapor volume fraction curve |
综上所述,通过分析背压对气穴的影响,可以发现在相同工况下,无背压时,气穴现象特别强烈;增大背压,阀口及出油口位置的气穴强度均随之减小.说明背压具有抑制气穴发生的作用,故液压系统中合理设置背压值对减小气穴具有重要的作用.
3 液压锥阀实验研究 3.1 液压系统原理图针对观测阀内流场气穴现象的目的,结合仿真研究的相关因素,设计了图 16所示的液压锥阀的液压回路原理图.采取控制变量法完成了不同工况下液压锥阀内流场气穴现象的实验研究.

|
1—过滤器; 2—温度计; 3—电机; 4—液压泵; 5、11—压力计; 6、10—压力传感器; 7—实验阀; 8—溢流阀; 9—流量传感器; 12—节流阀 图 16 液压系统回路图 Fig. 16 Circuit diagram of hydraulic system |
根据液压回路图,搭建了锥阀实验台如图 17所示,为了更加直观地观测锥阀内部气穴现象的变化规律,使用高透性有机玻璃(PMMA)材质加工了实验阀块,并加工了35°、40°、45°、50°半锥角的4个阀芯,借助高像素的相机拍摄各工况下阀口位置的气穴图像.由于阀块为有机玻璃材质,限于材质的强度,只能完成低压下各工况的实验测试,系统压力范围0~3 MPa.由于阀芯在正常工作时受到径向力的作用会产生径向偏移,在实验过程中很难通过定量地改变阀芯的径向偏移量来观察径向偏移对锥阀气蚀特性的影响,所以,本文仅做了半锥角,开口度以及背压对锥阀气穴的影响实验.

|
图 17 液压锥阀测试实验台 Fig. 17 Test rig of hydraulic cone valve |
如图 17所示的液压系统实物图,锥阀入口压力通过溢流阀来调定,在左侧压力表上实时观测;背压通过回油路上的背压节流阀来调定,在右侧压力表上实时观测;流量传感器通过采集数据在显示器上显示通流量.实验设备的具体型号如表 2所示.
| 表 2 实验设备 Tab. 2 Experimental equipment |
针对不同半锥角度对气穴现象的影响进行了实验研究,实验条件选择半锥角度分别为35°、40°、45°、50°的阀芯,背压0 MPa,开口度0.6 mm,依次在入口压力为0.5 MPa、1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa下进行实验.其中入口压力2 MPa工况下(下同)各半锥角的气穴现象如图 18所示,并将存在气穴现象的位置圈出.实验表明:随着半锥角增大,气穴强度明显增强,与本文2.2的仿真研究的变化趋势相同.并且通过圈出的气穴现象发生的明显位置,皆为阀芯上锥面的一侧,这与本文2.1仿真结果吻合.

|
图 18 不同半锥角下的气穴现象图 Fig. 18 Cavitation phenomena of different half cone angles |
针对开口度对气穴现象的影响进行了实验研究,实验条件选择开口度为0.4 mm、0.6 mm、0.8 mm、1.0 mm,半锥角45°的阀芯,背压为0 MPa,依次在入口压力为0.5 MPa、1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa下进行实验.不同开口度下拍摄的气穴现象如图 19所示.在开口度为0.4 mm时气穴的强度最明显.随着开口度增大,气穴现象的气团强度逐渐减弱.这与本文2.3仿真得到的随开口度变化的气穴现象强弱程度次序相同.

|
图 19 不同开口度下的气穴现象图 Fig. 19 Cavitation phenomena of different opening |
针对背压对气穴现象的影响进行了实验研究,实验条件选择背压为0 MPa、0.1 MPa、0.2 MPa、0.3 MPa,半锥角为45°的阀芯,开口度为0.6 mm,依次在入口压力为0.5 MPa、1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa下进行实验.实验得到不背压下气穴现象如图 20所示.可以看出4种背压下气穴强度由大到小的排列顺序依次为0 MPa、0.1 MPa、0.2 MPa、0.3 MPa.说明背压对气穴的发生有抑制作用,与本文2.4的仿真结果具有同样的规律性结论.

|
图 20 不同背压下的气穴现象图 Fig. 20 Cavitation phenomenon under different backpressure |
1) 通过分析锥阀内流场的压力和流场分布,发现阀芯两侧的流场分布不对称,得到径向力无法相互抵消的结论,然后计算出了阀芯在工作时存在的径向偏移,为后面的两相流仿真提供了理论依据.
2) 通过分析锥阀内流场的气穴分布及变化规律,得到结论:随着径向偏移量的增加,气穴主要聚集在上锥面一侧,下锥面一侧几乎不见气穴,且气穴强度随偏移量的增大而增强.故阀芯发生径向偏移,会引起气穴聚集,导致局部高度气蚀.
3) 通过实验与仿真结果进行对比,最终验证了仿真研究的正确性,并得到结论:综合通流能力、气穴强度衡量,半锥角为45°时是一个较优的阀芯半锥角度.
4) 增加开口度可以抑制阀口流场的气穴强度,但是当开口度过大时,也会引起出油口位置流场气穴的析出.同时,背压具有抑制气穴发生的作用,故液压系统中合理设置背压值对减小气穴具有重要的作用.
| [1] |
杨华勇, 王双, 张斌, 等. 数字液压阀及其阀控系统发展和展望[J]. 吉林大学学报(工), 2016, 46(5): 1494. YANG Huayong, WANG Shuang, ZHANG Bin, et al. Development and prospect of digital hydraulic valve and valve control system[J]. Journal of Jilin University (Engineering), 2016, 46(5): 1494. DOI:10.13229/j.cnki.jdxbgxb201605017 |
| [2] |
刘晓红, 柯坚. 基于计算流体动力学解析的液压锥阀噪声评价[J]. 中国机械工程, 2007, 18(22): 2687. LIU Xiaohong, KE Jian. Noise appraisement of hydraulic poppet valves based on CFD[J]. China Mechanical Engineering, 2007, 18(22): 2687. DOI:10.3321/j.issn:1004-132x.2007.22.010 |
| [3] |
冀宏, 傅新, 杨华勇. 内流道形状对溢流阀气穴噪声影响的研究[J]. 机械工程学报, 2002, 38(8): 19. JI Hong, FU Xin, YANG Huayong. A study on the effect of internal flow passage shape on cavitation noise of relief valve[J]. Journal of Mechanical Engineering, 2002, 38(8): 19. DOI:10.3321/j.issn:0577-6686.2002.08.004 |
| [4] |
傅新, 杜学文, 邹俊, 等. 孔隙高速流动中的气穴观测与噪声特性[J]. 机械工程学报, 2007, 43(4): 98. FU Xin, DU Xuewen, ZOU Jun, et al. Cavity observation and noise characteristics in high-speed pore flow[J]. Journal of Mechanical Engineering, 2007, 43(4): 98. DOI:10.3321/j.issn:0577-6686.2007.04.017 |
| [5] |
SHIGERU O, LEINO T, LINJAMA M. Experimental study on cavitation in water hydraulic poppet valve[J]. Transactions of the Japan Fluid Power System Society, 2002, 33(2): 29. DOI:10.5739/jfps.33.29 |
| [6] |
INOUE F, OUTA E, TAJIMI K, et al. An experimental study on control valve cavitation. (3rd Report. Vortex Shedding and Cavitation Inception on a Contoured Plug)[J]. Transactions of the Japan Society of Mechanical Engineers, 1993, 59(562): 1905. DOI:10.1299/kikaib.59.1905 |
| [7] |
UENO H, OKAJIMA A, TANAKA H, et al. Noisemeasurement and numerical simulation of oil flow in pressure control valves[J]. Jsme International Journal, 1994, 37(2): 336. DOI:10.1299/jsmeb.37.336 |
| [8] |
BERNAD S I, SUSANRESIGA R. Numerical model for cavitational flow in hydraulic poppet valves[J]. Modelling and Simulation in Engineering, 2012, 2012(1687-5591): 10. DOI:10.1155/2012/742162 |
| [9] |
CHEN Q, STOFFEL B. CFD simulation of a hydraulicconical valve with cavitation and poppet movement[C]//4th International Fluid Power Conference. Dresden: [s.n.], 2004: 331
|
| [10] |
YI Dayun, LU Liang, ZOU Jun, et al. Squeal noise in hydraulic poppet valves[J]. Journal of Zhejiang University-Science A(Applied Physics & Engineering), 2016, 17(4): 317. DOI:10.1631/jzus.A1400351 |
| [11] |
高殿荣, 王益群, 申功. 液压控制锥阀内流场的数值模拟与试验可视化研究[J]. 机械工程学报, 2002, 38(4): 66. GAO Dianrong, WANG Yiqun, SHEN Gong. Numerical simulation and experimental visualization of flow field in hydraulic control cone valve[J]. Journal of Mechanical Engineering, 2002, 38(4): 66. DOI:10.3321/j.issn:0577-6686.2002.04.014 |
| [12] |
王京涛, 吴张永, 岑顺锋, 等. 基于ANSYS的液压锥阀流场分析及结构优化[J]. 机床与液压, 2011, 39(13): 128. WANG Jingtao, WU Zhangyong, CEN Shunfeng, et al. Flow field analysis and structure optimization of hydraulic poppet valve based on ANSYS[J]. Machine Tool & Hydraulics, 2011, 39(13): 128. DOI:10.3969/j.issn.1001-3881.2011.13.038 |
| [13] |
谭剑波.液压锥阀气穴分析与流场参数化仿真[D].成都: 西南交通大学, 2014 TAN Jianbo. Hydraulic poppet valve cavitation analysis simulation of flow field parameters[D]. Chengdu: Southwest Jiaotong University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10613-1014257534.htm |
| [14] |
张健.液压锥型节流阀的气穴热效应及噪声的研究[D].哈尔滨: 哈尔滨工业大学, 2014 ZHANG Jian. Cavitation thermal effect and noise of hydraulic cone type throttle valve[D]. Haerbin: Harbin University of Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957199.htm |
| [15] |
易达云.锥阀振荡流场流动噪声增强机制研究[D].杭州: 浙江大学, 2015 YI Dayun.Study on the intensification mechanisms of flow-induced noise in the oscillating field of poppet valve[D]. Hangzhou: Zhejiang University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10335-1015630211.htm |
| [16] |
李光飞.基于液动力修正的锥阀振动特性研究[D].成都: 西南交通大学, 2013 LI Guangfei. The research on poppet valve vibration based on corrected hydrodynamic force[D]. Chengdu: Southwest Jiaotong University, 2013: 10 http://cdmd.cnki.com.cn/Article/CDMD-10613-1013250259.htm |
| [17] |
李光飞, 刘桓龙, 邓斌, 等. 液动力对锥阀振动特性的影响[J]. 机床与液压, 2014, 42(5): 28. LI Guangfei, LIU Huanlong, DENG Bin, et al. Effect of flow force to the poppet valve vibration[J]. Machine Tool & Hydraulics, 2014, 42(5): 28. DOI:10.3969/j.issn.1001-3881.2014.05.008 |
| [18] |
陆倩倩, 阮健, 李胜. 伯努利效应引起滑阀阀芯径向力的研究[J]. 中国机械工程, 2017(19): 2332. LU Qianqian, RUAN Jian, LI Sheng. Research on radial forces for hydraulic slide valves caused by bernoulli effect[J]. China Mechanical Engineering, 2017(19): 2332. DOI:10.3969/j.issn.1004-132X.2017.19.010 |
| [19] |
王建森, 王鹏飞, 冀宏, 等. 空化流动下液压锥阀所受推力的数值计算[J]. 兰州理工大学学报, 2017, 43(2): 54. WANG Jiansen, WANG Pengfei, JI Hong, et al. Numerical calculation of thrust on poppet valve under condition of cavitating flow[J]. Journal of Lanzhou University of Technology, 2017, 43(2): 54. DOI:10.3969/j.issn.1673-5196.2017.02.011 |
| [20] |
MAEDA T. Studies on the dynamic characteristics of a poppet valve: 2nd report, experimental analysis[J]. Bulletin of JSME, 1970, 13(56): 290. DOI:10.1299/jsme1958.13.290 |
| [21] |
钟英杰, 都晋燕, 张雪梅. CFD技术及在现代工业中的应用[J]. 浙江工业大学学报, 2003, 31(3): 284. ZHONG Yingjie, DU Jinyan, ZHANG Xuemei. CFD technology and application in modern industry[J]. Journal of Zhejiang University of Technology, 2003, 31(3): 284. DOI:10.3969/j.issn.1006-4303.2003.03.012 |
| [22] |
张迪嘉, 姜继海. 插装型液压锥阀流场与气穴仿真研究[J]. 液压与气动, 2016(4): 34. ZHANG Dijia, JIANG Jihai. Simulation of flow field and cavitation for hydraulic cartridge cone valve[J]. Chinese Hydraulics & Pneumatics, 2016(4): 34. DOI:10.11832/j.issn.1000-4858.2016.04.007 |
 2019, Vol. 51
2019, Vol. 51


