2. 山东大学 深圳研究院,广东 深圳 518057
2. Shenzhen Research Institute, Shandong University, Shenzhen 518057, Guangdong, China
拆卸序列规划(Disassembly Sequence Planning,DSP)旨在生成零件或子装配体的拆卸顺序[1],以满足拆卸成本、收益、拆卸方式等各种拆卸要求,其优劣程度直接影响着废旧产品进行再利用和再制造活动的有效性和经济性.产品拆卸根据拆卸深度可分为完全拆卸与选择拆卸两类[2],一般选择性拆卸应用较为广泛[3].本文主要对目标选择性拆卸序列规划问题进行研究.
目前,针对DSP问题,国内外学者已经开发了许多模型和方法,例如,AND/OR图法[4]、Petri网法[5]、拆卸波方法[2]以及各种启发式算法,例如,基于遗传算法[6-7]、粒子群算法[8]、人工蜂群算法[9]、蚁群算法[10-11]、花朵授粉算法[12]等的拆卸序列规划方法.上述研究主要集中在基于理想产品信息的拆卸模型构建[13]和算法开发上,而忽略了实际拆卸过程中许多零部件存在的故障缺陷问题对拆卸模型的影响.宋小文等[14]研究了零部件不可拆问题;JEREMY L等[15]通过产品服役时间与产品质量的关系进行拆卸序列评估;ZHAO Shuen等[16-17]基于模糊成本构建了产品拆卸序列决策模型.上述研究主要集中在产品不确定性质量对拆卸成本或收益的随机影响模型上,未考虑零部件故障问题对产品零部件拆卸关系的影响;同时,在实际拆卸中产品的质量既有随机性又有模糊性,需要通过专家意见进行评估.
为此,本文考虑到产品质量的不确定性,提取产品零部件的故障特征,采用专家意见和模糊函数确定零部件故障对拆卸模型元素的影响,并结合拆卸序列规划算法选择最佳拆卸序列方案,以提高拆卸序列的可行性和拆卸效率,降低拆卸的盲目性.
1 目标选择性拆卸信息模型 1.1 拆卸混合图模型拆卸混合图是一种产品拓扑结构模型,描述了产品零部件间的层次信息和约束关系,且易于计算机语言表达和实现,本文以拆卸混合图模型为基础进行研究.基本的产品拆卸混合图由三元组表示:
| $ \boldsymbol{G}=\langle\boldsymbol{V}, \boldsymbol{Z}, \boldsymbol{O}\rangle. $ | (1) |
式中:顶点集V={v1, v2, …, vn}表示产品的基本拆卸单元,如产品的零部件、子装配体等,n为基本拆卸单元的个数,产品拆卸混合图的顶点是基本拆卸单元各种信息的封装体,包括零部件或子装配体的标识、类型、几何特征及参数、数量、配合关系、剩余价值、质量状态、拆卸该零部件或子装配体所需的拆卸工具、拆卸方向、拆卸时间、拆卸收益等;Z={z1, z2, …, zl}为产品拆卸混合图的无向边集合,表示两零部件之间存在直接接触关系;O={o1, o2, …, om}为产品拆卸混合图的有向边集合,表示两零部件之间存在拆卸优先级关系.在实际拆卸过程中,零部件之间通常存在两种拆卸优先级关系:或优先约束和与优先约束,其定义如下:
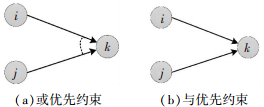
定义1 若零部件i和j都对零部件k同时存在优先约束,只需拆除零部件i和j中的任意一个,就能拆除零部件k,称零部件i和j为或关系,零部件i和j对零部件k的优先约束称为或优先约束(关联优先约束),在拆卸混合图模型中如图 1(a)所示.
|
图 1 两种优先约束关系 Fig. 1 Two constraints of priority |
定义2 若零部件i和j同时对零部件k存在优先约束,只有全部拆除零部件i和j,才能拆除零部件k,称零部件i和j为与关系,零部件i和j对零部件k的优先约束称为与优先约束(独立优先约束),在拆卸混合图模型中如图 1(b)所示.
根据产品拆卸混合图模型的顶点集、无向边集和有向边集,可构建接触约束矩阵M1和优先约束矩阵M2:
| $ \boldsymbol{M}_{1}=\left[\begin{array}{cccc}{A_{11}} & {A_{12}} & {\cdots} & {A_{1 n}} \\ {A_{21}} & {A_{22}} & {\cdots} & {A_{2 n}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {A_{n 1}} & {A_{n 2}} & {\cdots} & {A_{n n}}\end{array}\right]. $ |
式中
| $ {A_{ij}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{零件\;i\;和零件\;j\;存在接触约束;}\\ {0,}&{零件\;i\;和零件\;j\;不存在接触约束\;i = j.} \end{array}} \right. $ |
| $ \boldsymbol{M}_{2}=\left[\begin{array}{cccc}{B_{11}} & {B_{12}} & {\cdots} & {B_{1 n}} \\ {B_{21}} & {B_{22}} & {\cdots} & {B_{2 n}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {B_{n 1}} & {B_{n 2}} & {\cdots} & {B_{n n}}\end{array}\right]. $ |
式中:
| $ {B_{ij}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{零件\;i\;和零件\;j\;存在接触约束;}\\ {0,}&{零件\;i\;和零件\;j\;不存在接触约束\;i = j.} \end{array}} \right. $ |
式中n为基本拆卸单元的个数.则顶点i可拆卸必须满足式(2):
| $ \left(\sum\limits_{j=1}^{n} A_{i j}>0\right) \text { and }\left(\sum\limits_{j=1}^{n} B_{i j}=0\right). $ | (2) |
目标选择性拆卸旨在以最小的成本代价提取出产品中用户指定的目标零部件或子装配体.因此,拆卸成本是选择性拆卸序列规划的重要衡量标准.国内外学者通常选择拆卸工具变换次数、拆卸方向变换次数和拆卸时间作为产品拆卸成本的衡量指标,拆卸成本一般认为与拆卸时间相关,按文献[18]设定拆卸工具和方向变换的标准时间,可将目标函数统一量纲,如式(3)所示:
| $ F(\cos t)=\sum\limits_{j=1}^{n} w_{e} e_{i j} t_{e}+\sum\limits_{j=1}^{n} w_{d} d_{i j} t_{d}+\sum\limits_{j=1}^{n} w_{t} t_{j}. $ | (3) |
式中:
| $ {d_{ij}} = \left\{ \begin{array}{l} 1,零件\;i\;和\;j\;的拆卸方向不同;\\ 0,零件\;i\;和\;j\;的拆卸方向相同. \end{array} \right. $ |
F(cost)表示产品拆卸成本目标函数,tj表示拆卸零件j所需的拆卸时间,权重为wt,eij表示零件拆卸工具变化指标,权重为we,te表示拆卸工具变换一次的标准时间,dij表示零件拆卸方向变化指标,权重为wd,td表示拆卸方向变换一次的标准时间.
传统的拆卸信息模型一般基于理想产品信息构建,而产品在使用后一般存在多个故障缺陷.本文将考虑产品模糊故障信息对拆卸信息模型元素{Aj, Bj, ej, dj, tj}的影响,选择产品拆卸序列方案.
2 产品故障特征影响模型 2.1 典型故障特征与表达在实际拆卸过程中待拆卸对象的质量状态通常较差,存在多种故障特征,例如,磨损、变形、断裂、腐蚀、老化、孔洞、龟裂、松动、脱落等.根据产品故障特征对零部件几何特征和功能造成的影响,可将零部件故障特征分为5种类型,如表 1所示.按零部件是否存在相应的故障类型可建立产品零部件故障矩阵U,如式(4)所示:
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{u_{11}}}&{{u_{12}}}&{{u_{13}}}&{{u_{14}}}&{{u_{15}}}\\ {{u_{21}}}&{{u_{22}}}&{{u_{23}}}&{{u_{24}}}&{{u_{25}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{u_{n1}}}&{{u_{n2}}}&{{u_{n3}}}&{{u_{n4}}}&{{u_{n5}}} \end{array}} \right], $ | (4) |
| 表 1 故障特征类型 Tab. 1 Type of fault features |
式中
由于产品零部件的故障信息具有模糊性,采用模糊语言描述和量化,确定零部件故障的严重程度.本文将零部件i的故障fj(即:uij=1)的故障程度划分为五个等级,分别为S=[基本无故障,轻微故障,一般故障,中度故障,严重故障],对应评价值如式(5)所示.使用专家评判法确定故障程度,假设有N个专家分别对零部件i的故障fj进行评判,评判结果如式(6)所示:
| $ \boldsymbol{S}=\left[s_{1}, s_{2}, s_{3}, s_{4}, s_{5}\right]=[1,2,3,4,5], $ | (5) |
| $ \boldsymbol{H}=\left[h_{1}, h_{2}, h_{3}, h_{4}, h_{5}\right]. $ | (6) |
式中:
| $ r_{i j}=\boldsymbol{S} \cdot \boldsymbol{H}^{\mathrm{T}}, $ | (7) |
式中rij为零部件i的故障fj的模糊特征值,rij越大,表明零部件i的fj故障越严重.利用式(7)可将式(4)转化成产品零部件的故障特征值矩阵R:
| $ \boldsymbol{R}=\left[\begin{array}{ccccc}{u_{11} r_{11}} & {u_{12} r_{12}} & {u_{13} r_{13}} & {u_{14} r_{14}} & {u_{15} r_{15}} \\ {u_{21} r_{21}} & {u_{22} r_{22}} & {u_{23} r_{23}} & {u_{24} r_{24}} & {u_{25} r_{25}} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {u_{n 1} r_{n 1}} & {u_{n 2} r_{n 2}} & {u_{n 3} r_{n 3}} & {u_{n 4} r_{n 4}} & {u_{n 5} r_{n 5}}\end{array}\right]. $ |
式中
uijrij为零部件i的fj故障的模糊特征值,则零部件i的故障特征值矩阵为
| $ \boldsymbol{R}_{i}=\left[\begin{array}{lllllll}{u_{i 1} r_{i 1}} & {u_{i 2} r_{i 2}} & {u_{i 3} r_{i 3}} & {u_{i 4} r_{i 4}} & {u_{i 5} r_{i 5}}\end{array}\right]. $ | (8) |
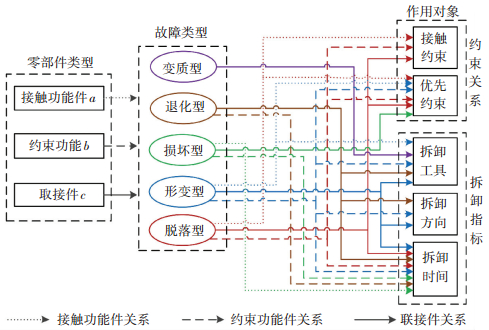
在实际的拆卸操作中,拆卸信息模型中的元素是否受到影响与零部件类型和故障类型相关.根据零部件的约束关系和功能,零部件可以分为3种类型,如表 2所示.不同类型零部件的故障与拆卸模型元素的关系一般如图 2所示,图中连接线表示连接线双方存在影响关系.根据图 2零部件类型与故障类型是否对拆卸模型元素产生影响,若产生影响,值为1,否则值为0,可分别建立接触功能件、约束功能件和联接件的故障类型与拆卸模型元素的关联矩阵la、lb、lc,如公式(9)所示:
| $ \begin{array}{l} {\mathit{\boldsymbol{l}}_a} = \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} A&B&e&d&t \end{array}}&{}\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&1\\ 0&1&1&0&0\\ 1&1&0&0&0 \end{array}} \right]}&{\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ {{f_3}}\\ {{f_4}}\\ {{f_5}} \end{array}} \end{array},\\ {\mathit{\boldsymbol{l}}_b} = \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} A&B&e&d&t \end{array}}&{}\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&1\\ 0&0&0&0&1\\ 0&1&1&1&1\\ 1&1&0&0&1 \end{array}} \right]}&{\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ {{f_3}}\\ {{f_4}}\\ {{f_5}} \end{array}} \end{array},\\ {\mathit{\boldsymbol{l}}_c} = \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} A&B&e&d&t \end{array}}&{}\\ {\left[ {\begin{array}{*{20}{c}} 0&0&1&0&0\\ 0&0&1&1&1\\ 0&1&0&0&0\\ 0&0&1&1&0\\ 1&1&0&0&1 \end{array}} \right]}&{\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ {{f_3}}\\ {{f_4}}\\ {{f_5}} \end{array}} \end{array}. \end{array} $ | (9) |
| 表 2 产品零部件类型 Tab. 2 Type of product parts |
|
图 2 不同零部件的各类故障与拆卸模型元素的关系 Fig. 2 Relationship between various faults of different parts and disassembly model elements |
由零部件i的故障特征值矩阵(8)和关联矩阵(9),可推导得出零部件i的故障类型与拆卸模型元素的关联度矩阵αi:
1) 若零部件i为接触功能件,其关联度矩阵αi为
| $ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_i} = {\mathit{\boldsymbol{R}}_i}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_a} = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&{{u_{i3}}{r_{i3}}}\\ 0&{{u_{it}}{r_{i4}}}&{{u_{ij}}{r_{i4}}}&0&0\\ {{u_{i5}}{r_{i5}}}&{{u_{i5}}{r_{i5}}}&0&0&0 \end{array}} \right], \end{array} $ |
2) 若零部件i为约束功能件,其关联度矩阵αi为
| $ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_i} = {\mathit{\boldsymbol{R}}_i}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{{u_{i2}}{r_{i2}}}\\ 0&0&0&0&{{u_{i3}}{r_{i3}}}\\ 0&{{u_{i4}}{r_{i4}}}&{{u_{i4}}{r_{i4}}}&{{u_{i4}}{r_{i4}}}&{{u_{i4}}{r_{i4}}}\\ {{u_{i5}}{r_{i5}}}&{{u_{i5}}{r_{i5}}}&0&0&{{u_{i5}}{r_{i5}}} \end{array}} \right], \end{array} $ |
3) 若零部件i为联接件,其关联度矩阵αi为
| $ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_i} = {\mathit{\boldsymbol{R}}_i}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_c} = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&0&{{u_{i1}}{r_{i1}}}&0&0\\ 0&0&{{u_{i2}}{r_{i2}}}&{{u_{i2}}{r_{i2}}}&{{u_{i2}}{r_{i2}}}\\ 0&{{u_{i3}}{r_{i3}}}&0&0&0\\ 0&0&{{u_{i4}}{r_{i4}}}&{{u_{i4}}{r_{i4}}}&0\\ {{u_{i5}}{r_{i5}}}&{{u_{i5}}{r_{i5}}}&0&0&{{u_{i5}}{r_{i5}}} \end{array}} \right]. \end{array} $ |
为确定零部件各类故障的故障程度对拆卸模型元素的模糊影响度和影响结果,使用模糊三角函数作为评判结果的隶属度函数.将零部件故障特征对拆卸模型元素的影响结果分别划分评判等级和等级值,分别如下:
1) 对接触约束的影响等级划分为MA= [a0, a1]=[0, 1],式中:a0表示不需要更改接触约束,a1表示需要更改接触约束.
2) 对优先约束的影响等级划分为MB= [b0, b1]=[0, 1],式中:b0表示不需要更改优先约束,b1表示需要更改优先约束.
3) 对拆卸工具的影响等级划分为E=[e0, e1]=[0, 1],式中:e0表示不需要更换拆卸工具或使用额外的辅助拆卸工具,e1表示需要更换拆卸工具或使用额外的辅助拆卸工具.
4) 对拆卸方向的影响等级划分为D=[d0, d1]=[0, 1],式中:d0表示不需要改变拆卸方向,d1表示需要改变拆卸方向.
5) 对拆卸时间的影响等级划分为T=[t0, k1t, k2t, …, kit],式中:t0表示不需要改变拆卸时间,按原拆卸时间计算,其值为0,kit表示需要增加ki倍的原拆卸时间.
根据零部件故障特征对拆卸模型元素影响结果的等级划分,采用模糊三角函数分别表达各影响结果等级的隶属度函数.若论域N上的模糊数为m,则m的隶属度函数μ
| $ {\mu _{\tilde m}}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{x - {m_1}}}{{{m_2} - {m_1}}},}&{{m_1} \le x < {m_2}};\\ {\frac{{{m_3} - x}}{{{m_3} - {m_2}}},}&{{m_2} \le x < {m_3}};\\ {\;\;\;\;\;0,}&{x \le {m_1}\;{\rm{ or }}\;x \ge {m_3}.} \end{array}} \right. $ | (10) |
| $ {\mu _{\tilde m}}(x) = \left\{ {\begin{array}{*{20}{c}} {1,}&{x < {m_1};}\\ {\frac{{{m_2} - x}}{{{m_2} - {m_1}}},}&{{m_1} \le x < {m_2};}\\ {0,}&{x \ge {m_2}.} \end{array}} \right. $ | (11) |
| $ {\mu _{\tilde m}}(x) = \left\{ {\begin{array}{*{20}{c}} {0,}&{x < {m_1};}\\ {\frac{{x - {m_1}}}{{{m_2} - {m_1}}},}&{{m_1} \le x < {m_2};}\\ {1,}&{x \ge {m_2}.} \end{array}} \right. $ | (12) |
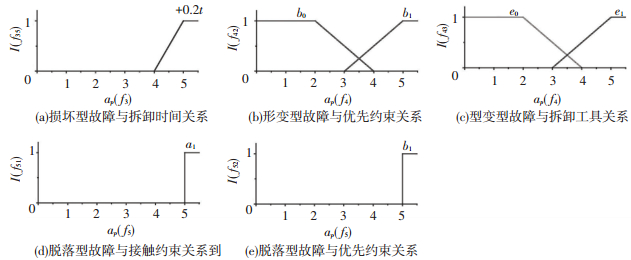
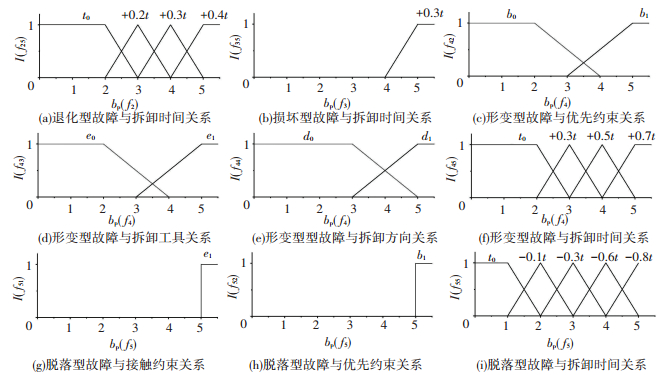
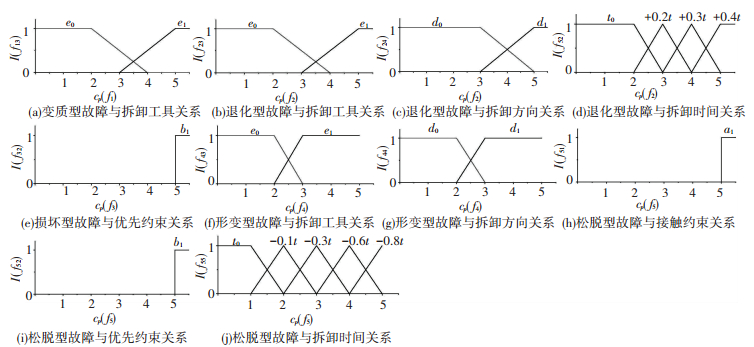
由于不同类型零部件的故障特征对拆卸模型元素的影响存在差异,因此,根据关联矩阵(9)和式(10)~(12)分别对接触功能件、约束功能件和联接件设置隶属度函数,则接触功能件、约束功能件和联接件的各类故障与其影响结果等级的隶属度函数分别如图 3~5所示(隶属度函数可根据产品情况调整),图中横坐标表示零件某类故障与某一拆卸模型元素的关联度值,纵坐标表示相应拆卸模型元素影响结果等级的隶属度.由此可确定零部件故障对拆卸模型元素的影响值,若零部件i的fj故障与拆卸模型元素g的关联度值为uijrij,根据隶属度函数,可以确定fj故障对拆卸模型元素g在rij值时的影响结果等级值Φijg=[
| $ q_{ij}^g = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ij}^g \cdot \mathit{\boldsymbol{I}}_{ij}^{g{\rm{T}}} = \sum\limits_{k = 1} {{\varphi _k}} \cdot \Delta {i_k}. $ | (13) |
|
图 3 接触功能件的各类故障对相应拆卸模型元素影响结果等级的隶属度函数 Fig. 3 Membership functions of the effect-level of various faults of a on corresponding disassembly model elements |
|
图 4 约束功能件的各类故障对相应拆卸模型元素影响结果等级的隶属度函数 Fig. 4 Membership functions of the effect-level of various faults of b on corresponding disassembly model elements |
|
图 5 联接件的各类故障对相应拆卸模型元素影响结果等级的隶属度函数 Fig. 5 Membership functions of the effect-level of various faults of c on corresponding disassembly model elements |
式中qijg表示零部件i的fj故障对拆卸模型元素g的影响值.
根据式(13)零部件故障类型的影响度和专家给定的阈值,可决定是否修正对应的拆卸模型元素,如式(14)~(18)所示:
| $ \left\{ {\begin{array}{*{20}{c}} {q_{ij}^A \le Q_{ij}^A,}&{无需修正零件\;i\;的接触约束;}\\ {Q_{ij}^A < q_{ij}^A < 1,}&{需要修正零件\;i\;的接触约束;}\\ {q_{ij}^A = 1,}&{去除零件\;i\;的接触约束.} \end{array}} \right. $ | (14) |
| $ \left\{ {\begin{array}{*{20}{c}} {q_{ij}^B \le Q_{ij}^B,}&{无需修正零件\;i\;的接触约束;}\\ {Q_{ij}^B < q_{ij}^B < 1,}&{需要修正零件\;i\;的接触约束;}\\ {q_{ij}^B = 1,}&{去除零件\;i\;的接触约束.} \end{array}} \right. $ | (15) |
| $ e_i^ * = \left\{ {\begin{array}{*{20}{c}} {{e_i} + 1,}&{q_{ij}^e > Q_{ij}^e\;则需要更换和使用辅助工具;}\\ {{e_i},}&{q_{ij}^e \le Q_{ij}^e\;则无需更换和使用辅助工具.} \end{array}} \right. $ | (16) |
| $ d_i^ * = \left\{ {\begin{array}{*{20}{c}} {{d_i} + 1,}&{q_{ij}^d > Q_{ij}^d\;则需要更改零件\;i\;拆卸方向;}\\ {{d_i},}&{q_{ij}^d \le Q_{ij}^d\;则无需更改零件\;i\;拆卸方向.} \end{array}} \right. $ | (17) |
| $ t_{i}^{*}=t_{i}+\sum\limits_{j=1}^{5} q_{i j}^{t}. $ | (18) |
式中:ti*表示零部件i修正后的拆卸时间,ti表示零部件i的原拆卸时间,ei*表示拆卸零部件i的修正拆卸工具变换次数,ei表示拆卸零部件i的原拆卸工具变换次数,di*表示拆卸零部件i的修订拆卸方向变换次数,di表示拆卸零部件i的原拆卸方向变换次数,QijA, QijB, Qije, Qijd, Qijt分别为修正阈值,由专家给出.
3 基于产品故障特征的拆卸序列规划 3.1 修正拆卸信息模型按产品的故障特征和影响结果,对传统产品拆卸混合图模型进行修正和补充得到故障拆卸混合图模型,用六元组表示:
| $ \boldsymbol{G}=\left\langle\boldsymbol{V}_{a}, \boldsymbol{V}_{b}, \boldsymbol{V}_{c}, \boldsymbol{V}_{u}, \boldsymbol{Z}^{*}, \boldsymbol{O}^{*}\right\rangle. $ |
式中:Va表示接触功能件顶点集合,Vb表示约束功能件顶点集合,Vc表示联接件顶点集合,Vu表示故障零部件顶点集合,Z*表示修正无向边集合,O*表示修正有向边集合.根据故障拆卸混合图,可重新构建修正接触约束矩阵M1*和修正优先约束矩阵M2*.
同时,根据修正拆卸工具变换次数、修正拆卸方向变换次数和修正拆卸时间,重新构建拆卸序列优化的目标函数,如式(19)所示:
| $ F(\cos t)^{*}=\sum\limits_{j=1}^{n} w_{e} e_{i j}^{*} t_{e}+\sum\limits_{j=1}^{n} w_{d} d_{i j}^{*} t_{d}+\sum\limits_{j=1}^{n} w_{t} t_{j}^{*}. $ | (19) |
式中:F(cos t)*表示产品修正拆卸成本目标函数,tj*表示拆卸零部件j所需的修正拆卸时间,eij*表示零部件修正拆卸工具变换指标,dij*表示零部件修正拆卸方向变换指标.
3.2 拆卸序列规划遗传算法遗传算法借鉴自然进化规律以得到最优个体,具有全局寻优性、鲁棒性等特点,因此本文结合遗传算法进行拆卸序列优化.
对于DSP问题,遗传算法可直接使用零部件编号进行编码,例如个体编码(4, 3, 7, 5, 1, 2, 6)表示需要拆卸的零部件编号依次为:4→3→7→5→1→2→6.
交叉操作采用双点交叉,假设有2个体A和B,随机产生2个交叉位置,将2个交叉位置之间的部分进行互换,剔除重复零件编号并依次补充缺失的零部件编号,生成2个新个体A*和B*,例如:
| $ \begin{array}{l} \Rightarrow \begin{array}{*{20}{c}} {个体\;A:6\;3}\\ {个体\;A:3\;4} \end{array}\left| {\begin{array}{*{20}{c}} 4&7&1\\ 5&7&2 \end{array}} \right.\left| {\begin{array}{*{20}{c}} 5&2\\ 1&6 \end{array}} \right. \Rightarrow 交叉:\begin{array}{*{20}{c}} 6&3\\ 3&4 \end{array}\left| {\begin{array}{*{20}{c}} 5&7&2\\ 4&7&1\\ - &{}&{} \end{array}} \right.\left| {\begin{array}{*{20}{c}} 1&2\\ {}& - \\ 1&6\\ - &{} \end{array}} \right.\\ \Rightarrow \left( {去除重复编号并补充缺少编号} \right)\\ \begin{array}{*{20}{c}} {新个体\;{A^ * }:6\;3\;5\;7\;2\;1\;4}\\ {新个体\;{B^ * }:3\;4\;2\;{\rm{7}}\;{\rm{1}}\;{\rm{5}}\;{\rm{6}}} \end{array} \end{array} $ |
变异操作采用单点变异,假设拆卸序列个体A:(1, 3, 2, 4, 5, 6, 7),若随机产生的变异位置分别为第3位和第7位,将第3位置上的零部件编号移到第7位置上,产生新个体A*:(1, 3, 4, 5, 6, 7, 2).
若经过交叉和变异的子个体的适应度优于父个体,则用子个体替换父个体形成新的群体,并遗传到下一代.拆卸序列遗传算法的主要步骤如下:
Step 1 设置种群大小popsize,交叉概率pcro,变异概率pmut,最大迭代次数pgen,随机产生一组个体,构成初始种群.
Step 2 计算种群中个体的适应度值Fi(cost)*,并保存当前种群中的最优个体,并判断是否满足收敛条件,若满足执行step 7,否则执行step 3至step 6.
Step 3 执行选择操作,复制新群体遗传到下一代.
Step 4 将种群个体两两随机配对,若随机数rand[0, 1] < pcro,则执行双点交叉操作;否则不执行交叉操作.
Step 5 若随机数rand[0, 1] < pmut,则执行单点变异操作;否则不执行变异操作.
Step 6 若子个体的适应度优于父个体,则用子个体替换父个体,返回Step 2.
Step 7 输出适应度最优的个体和适应度值.
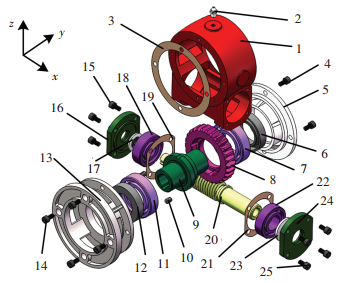
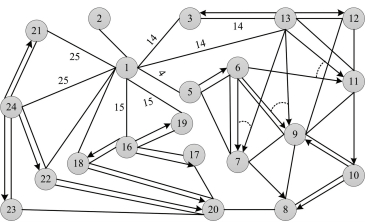
4 实例以涡轮减速器为例,分析其故障因素对拆卸信息模型的影响,选择拆卸序列方案.涡轮减速器由25个零部件组成,如图 6所示.零部件的原始拆卸信息如表 3所示.根据产品装配关系和空间位置约束,可得出涡轮减速器的原始拆卸混合图,如图 7所示,图中无向边上的数字为联接件的编号,表示无向边两边的顶点由联接件连接,无向边上的联接件在拆卸时优先于两端顶点.据统计,涡轮减速器主要存在油封、密封垫破损,蜗杆、蜗轮磨损或损坏,轴承生锈、腐蚀或损坏,螺栓生锈、腐蚀、松动,传动装置固定不良等故障.
|
图 6 涡轮减速器产品图 Fig. 6 Drawing of turbine reducer |
| 表 3 涡轮减速器零部件信息表 Tab. 3 Information table of turbine reducer parts |
|
图 7 涡轮减速器原始混合图模型 Fig. 7 Original hybrid graph model of turbine reducer |
为了便于进行拆卸序列规划,可根据涡轮减速器存在的故障特征,对涡轮减速器进行简单分类.某一类涡轮减速器主要存在零件17磨损、断裂,零件6、12和23磨损,零件8磨损、断裂,零件25松动、腐蚀,零件15腐蚀,零件18变形损坏故障.利用式(4)建立涡轮减速器零部件故障矩阵U,如式(20)所示,为便于表达,式中已将部分无故障的零部件省略.根据10位专家对零部件各类故障程度的评估,利用式(7)计算各零部件故障的模糊特征值,如表 4所示.根据式(20)和表 4可得到涡轮减速器零部件的故障特征值矩阵R,如式(21)所示.
| 表 4 零部件故障的模糊特征值 Tab. 4 Fuzzy values of parts failures |
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&1&0&0&0\\ 0&0&0&0&0\\ 0&1&1&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&1&0&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&1&0&0&0\\ 0&0&0&0&0\\ 0&1&1&0&0\\ 0&0&0&1&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&1&0&0&0\\ 0&0&0&0&0\\ 0&1&0&0&1 \end{array}} \right]\begin{array}{*{20}{c}} \vdots \\ 6\\ 7\\ 8\\ \vdots \\ {12}\\ \vdots \\ {15}\\ {16}\\ {17}\\ {18}\\ \vdots \\ {23}\\ {24}\\ {25} \end{array} $ | (20) |
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&{3.1}&0&0&0\\ 0&0&0&0&0\\ 0&{3.5}&{4.8}&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&{3.1}&0&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&{2.4}&0&0&0\\ 0&0&0&0&0\\ 0&{3.1}&{4.6}&0&0\\ 0&0&0&{4.6}&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&{3.1}&0&0&0\\ 0&0&0&0&0\\ 0&{2.4}&0&0&{2.2} \end{array}} \right]\begin{array}{*{20}{c}} \vdots \\ 6\\ 7\\ 8\\ \vdots \\ {12}\\ \vdots \\ {15}\\ {16}\\ {17}\\ {18}\\ \vdots \\ {23}\\ {24}\\ {25} \end{array} $ | (21) |
根据出现故障的零部件类型,利用式(9)和式(21)可分别得出各故障零部件的故障特征与拆卸模型元素的关联度矩阵,如下所示:
| $ \begin{array}{*{20}{c}} {{\alpha _6} = {\mathit{\boldsymbol{R}}_6}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{3.1}\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array}\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{\alpha _8} = {\mathit{\boldsymbol{R}}_8}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{3.5}\\ 0&0&0&0&{4.8}\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\alpha _{12}} = {R_{12}}^{\rm{T}} \otimes {l_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{3.1}\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array}\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{\alpha _{15}} = {\mathit{\boldsymbol{R}}_{15}}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_c} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&{2.4}&{2.4}&{2.4}\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\alpha _{17}} = {\mathit{\boldsymbol{R}}_{17}}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{3.1}\\ 0&0&0&0&{4.6}\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array}\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{\alpha _{18}} = {\mathit{\boldsymbol{R}}_{18}}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&{4.6}&{4.6}&{4.6}&{4.6}\\ 0&0&0&0&0 \end{array}} \right],} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\alpha _{23}} = {\mathit{\boldsymbol{R}}_{23}}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_b} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&{3.1}\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right],} \end{array}\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{\alpha _{25}} = {\mathit{\boldsymbol{R}}_{25}}^{\rm{T}} \otimes {\mathit{\boldsymbol{l}}_c} = }\\ {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&{2.4}&{2.4}&{2.4}\\ 0&0&0&0&0\\ 0&0&0&0&0\\ {2.2}&{2.2}&0&0&{2.2} \end{array}} \right].} \end{array} $ |
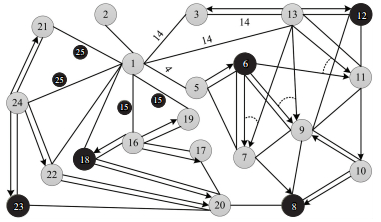
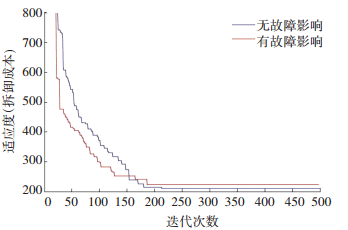
根据关联度矩阵,使用式(13)和图 3~图 5中的隶属度函数分别计算故障零部件的影响度,并修正拆卸模型元素,如表 5所示.拆卸元素修正后重新构建涡轮减速器的故障混合图模型,如图 8所示,图中黑色节点表示出现故障的零部件,其修正的拆卸信息如表 5所示.基于图 8及其修正后的拆卸元素,以式(19)作为目标适应度函数,式中te=8 s,td=4 s,权重比为:we:wd:wt=1:1:1,以零件20作为目标零件,运用遗传算法进行拆卸序列规划,并与不考虑故障因素的拆卸序列规划结果作对比,分别设置种群大小popsize=30,交叉概率pcro=0.7,变异概率pmut=0.1,最大迭代次数pgen=500,则两种情况的迭代收敛曲线和结果分别如图 10和表 6所示.受产品故障的模糊影响,导致拆卸零件20的拆卸成本增加,但未改变最优拆卸序列路径,更切合实际的拆卸过程,降低了拆卸的盲目性.
|
图 8 涡轮减速器故障混合图模型 Fig. 8 Fault-hybrid graph model for turbine reducer |
| 表 5 蜗轮减速器故障零部件的影响度与拆卸模型元素修正 Tab. 5 Influence degree of failure parts to turbine reducer and modification of dismantling model elements |
|
图 10 拆卸目标零部件20的收敛曲线 Fig. 10 Convergent curve to dismantle part 20 |
| 表 6 蜗杆拆卸序列优化结果 Tab. 6 Optimization results of disassembly sequence to worm |
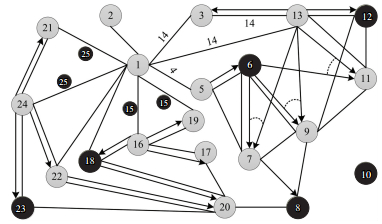
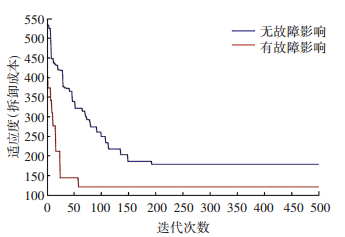
假设有一涡轮减速器除了出现以上故障外,零件10存在脱落故障,即q10 5A=1; q10 5B=1.根据故障特征建立故障混合图模型,如图 9所示.基于图 9,以零件8作为目标零件,运用上述遗传算法设置进行拆卸序列规划,并与不考虑故障因素的拆卸序列规划结果作对比,两种情况的迭代收敛曲线和结果分别如图 11和表 7所示.受产品故障的模糊影响,拆卸零件8时不需要再拆卸零件11和10,拆卸序列由“4-5-7-11-10-8”优化为“4-5-7-8”,优化了拆卸序列路径,极大地提高了拆卸序列在实际拆卸过程中的可行性,拆卸成本也由178 s降低为120.92 s,拆卸成本降低了32.07%,明显提高了拆卸效率,降低了拆卸盲目性.
|
图 9 涡轮减速器故障混合图模型 Fig. 9 Fault-hybrid graph model for turbine reducer |
|
图 11 拆卸目标零部件8的收敛曲线 Fig. 11 Convergent curve to dismantle part 8 |
| 表 7 涡轮拆卸序列优化结果 Tab. 7 Optimization results of disassembly sequence to worm wheel |
本文针对待拆卸对象普遍存在模糊性故障问题,分析了产品故障特征对拆卸模型的模糊影响,提出了考虑产品故障特征的目标选择性拆卸序列规划方法.本文选择拆卸混合图模型来表达产品拆卸信息;通过提取产品可能存在的故障,运用专家评价法推导了零部件故障与拆卸模型元素的关联度矩阵,并利用模糊函数计算零部件故障对拆卸模型元素的影响度,以此修正拆卸模型元素和拆卸信息;在拆卸混合图模型的基础上考虑零部件故障问题,构造了故障拆卸混合图模型,并结合遗传算法生成了切合实际的拆卸序列方案.所提方法较好地解决了产品故障对拆卸造成的模糊影响,极大地提高了拆卸序列在实际拆卸过程中的可行性和拆卸效率,有效降低了拆卸的盲目性.
未来的研究中,需要进一步研究如何精确提取和量化零部件故障;同时,还应进一步量化考虑对拆卸收益、环境成本等指标的模糊影响.
| [1] |
TANG Ying, ZHOU Mengchu, EYAL Z. Disassembly modeling, planning, and application[J]. Journal of Manufacturing Systems, 2002, 21(3): 200. DOI:10.1016/S0278-6125(02)80162-5 |
| [2] |
SRINIVASAN H, GADH R. A geometric algorithm for single selective disassembly using the wave propagation abstraction[J]. Computer Aided Design, 1998, 30(8): 603. DOI:10.1016/S0010-4485(98)00009-8 |
| [3] |
邢宇飞, 王成恩, 柳强. 基于Pareto解集蚁群算法的拆卸序列规划[J]. 机械工程学报, 2012, 48(09): 186. XING Yufei, WANG Chengen, LIU Qiang. Disassembly sequence planning based on pareto ant colony algorithm[J]. Journal of Mechanical Engineering, 2012, 48(09): 186. |
| [4] |
MOORE K E, GUNGOR A, GUPTA S M. Petri netapproach to disassembly process planning for products with complex AND/OR precedence relationships[J]. European Journal of Operational Research, 2001, 135(2): 428. DOI:10.1016/S0377-2217(00)00321-0 |
| [5] |
TANG Ying, ZHOU Mengchu, GAO Meimei. Fuzzy-etri-net-based disassembly planning considering human factors[J]. IEEE Transactions on Systems, Man., and Cybernetics, Part A, 2006, 36(4): 718. DOI:10.1109/TSMCA.2005.853508 |
| [6] |
WANG Hui, XIANG Dong, DUAN Guanghong. A genetic algorithm for product disassembly sequence planning[J]. Neuro-computing, 2008, 71(13/14/15): 2720. |
| [7] |
REN Yaping, ZHANG Chaoyong, FU Zhao, et al. An asynchronous parallel disassembly planning based on genetic algorithm[J]. European Journal of Operational Research, 2018, 269(2): 647. DOI:10.1016/j.ejor.2018.01.055 |
| [8] |
徐进, 张树有, 费少梅. 基于自适应粒子群的产品再制造拆卸规划[J]. 浙江大学学报(工学版), 2011, 45(10): 1746. XU Jin, ZHANG Shuyou, FEI Shaomei. Product remanufacture disassembly planning based on adaptive particle swarm optimization algorithm[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(10): 1746. DOI:10.3785/j.issn.1008-973X.2011.10.008 |
| [9] |
宋守许, 张文胜, 张雷. 基于改进人工蜂群算法的产品拆卸序列规划[J]. 中国机械工程, 2016, 27(17): 2384. SONG Shouxu, ZHANG Wensheng, ZHANG Lei. Product disassembly sequence planning based on improved artificial bee colony algorithm[J]. China Mechanical Engineering, 2016, 27(17): 2384. DOI:10.3969/j.issn.1004-132X.2016.17.019 |
| [10] |
章小红, 李世其, 王峻峰. 基于蚁群算法的产品拆卸序列规划方法[J]. 计算机辅助设计与图形学学报, 2007, 19(03): 387. ZHANG Xiaohong, LI Shiqi, WANG Junfeng. Product disassembly sequence planning based on ant colony optimization[J]. Journal of Computer-aided Design & Computer Graphics, 2007, 19(03): 387. DOI:10.3321/j.issn:1003-9775.2007.03.021 |
| [11] |
WANG W, SHI X. Disassembly sequence planning based on poisoning antcolony algorithm[J]. Adv. Des. Manuf, 2014, 572(1): 340. |
| [12] |
焦庆龙, 徐达, 李闯. 基于花朵授粉算法的产品拆卸序列规划[J]. 计算机集成制造系统, 2016, 22(12): 2791. JIAO Qinglong, XU Da, LI Chuang. Product disassembly sequence planning based on flower pollination algorithm[J]. Computer Integrated Manufacturing Systems, 2016, 22(12): 2791. |
| [13] |
YOUSSIF M M, ALKADEEM R A, DARDIRY M A. Incorporating ergonomic factors in disassembly sequence planning[J]. Alexandria Engineering Journal, 2011, 50(3): 213. DOI:10.1016/j.aej.2011.01.016 |
| [14] |
宋小文, 潘兴兴, 冯坤, 等. 面向零件不可拆的复杂产品拆卸序列规划[J]. 计算机集成制造系统, 2013, 19(6): 1249. SONG Xiaowen, PAN Xingxing, FENG Kun, et al. Complex product disassembly sequence planning oriented to defective parts[J]. Computer Integrated Manufacturing Systems, 2013, 19(6): 1249. |
| [15] |
JEREMY L R, JAIME A C. Partial disassembly sequencing considering acquired end-of-life product age distributions[J]. International Journal of Production Research, 2014, 52(24): 7496. DOI:10.1080/00207543.2014.939237 |
| [16] |
ZHAO Shuen, LI Yuling, FU Rui, et al. Fuzzy reasoning Petri nets and its application to disassembly sequence decision-making for the end-of-life product recycling and remanufacturing[J]. International Journal of Computer Integrated Manufacturing, 2014, 27(5): 415. DOI:10.1080/0951192X.2012.717714 |
| [17] |
TIAN G, ZHOU M, LI P. Disassembly sequence planning considering fuzzy component quality and varying operational cost[J]. Transactions on Automation Science and Engineering, 2018, 15(2): 748. DOI:10.1109/TASE.2017.2690802 |
| [18] |
陈弋文, 陈伟达. 基于收益概率的不确定环境下的产品拆卸序列优化[J]. 计算机集成制造系统, 2014, 20(4): 793. CHEN Yiwen, CHEN Weida. Product disassembly sequence optimization based on profit-probability under uncertain environment[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 793. |
 2019, Vol. 51
2019, Vol. 51


