仿生学的进展促使流动控制技术发展,由此也衍生出流动控制相关技术领域另一个重要的分支——仿生流动控制[1-2].仿生流动控制是通过模拟自然界中生物某些场合下的特定机能[3-4],从而减小流体介质中的流动阻力,提高升力,降低由流动产生的噪声[5-6].
针对仿生流动控制方面国内外学者进行一定的科学研究. Gograve[7]等在低速风洞试验中,研究弦长雷诺数为1×106的情况下翼型安装气动弹片引起的增升效果,与原始翼型相比,加装气动弹片的翼型最大升力可增加约20%,进一步表明气动弹片的有效加装能够使翼型气动性能一定程度上得到较为明显的改善. Graham[8]对于鸮类静音飞行的机理进行大量的研究,指出其覆羽、翅膀前缘的锯齿状结构是其能够保持静音飞行的根本所在. Geyer[9-10]等对鸮类羽毛结构进行降噪效果的研究得到了同样的结论.基于仿鲨鱼皮所制得的泳衣,减阻效果明显,且已经在生活中大量应用. 2000[11]年悉尼奥运会的游泳项目中此仿生泳衣助选手获得28枚金牌.张学迅[12]通过实验与数值模拟相结合的方法,发现锯齿尾缘结构对于尾涡结构的改善效果明显,且使得叶片尾迹区域的展向相关性有所减弱,同时远场辐射的噪声有所降低.姜琓[13]等从仿生学出发,对跨介质飞行器进行改进,发现了其可行性与科学性. Schlüter[14]研究自适应襟翼在两种翼型SD8020与NACA4412翼型上的作用效果,发现翼型布置自适应襟翼后,最大升力较原始翼型均出现一定程度的提升.廖庚华[15]对长耳鸮翅膀建立三维实体模型并进行气动及声学特性研究,发现其在动力机械方面的运用价值.仿生流动控制的研究及应用已经取得较好的成果,本文模仿鸟类飞行时翅膀对流动分离的控制,建立翅片翼模型,改变结构参数并进行气动特性分析.
1 翼型模型及数值计算 1.1 仿生翅片翼型模型建立在自然界中鸟类飞行时,在遇到俯冲或是阵风等不同况导致翅膀表面的流体发生分离时,表面小的覆羽张开以应对流动分离的发展及恶劣影响.基于此,本文设计出应用于风力机的一种仿生翅片翼,如图 1所示.
|
图 1 实物模型 Fig. 1 Physical model |
以NACA0018翼型为基础翼型,弦长C=0.25 m,在距翼型前缘点d/c倍弦长处的吸力面布置长为l/c倍弦长的固定仿生翅片翼,如图 2所示.其中仿生翅片翼抬起角度θ.
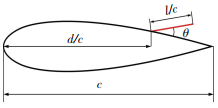
|
图 2 仿生翅片翼计算模型 Fig. 2 A model of bionic fin-wing calculation |
采用计算流体力学软件ANASYS Fluent 17.0计算翼型所受气动力及周围流场,采用压力与速度耦合的方法求解N-S流动控制方程.基于涡粘性假设,采用SST k-ω湍流模型求解湍流附加应力.
图 3为计算域结构与边界条件.计算域包含两部分:内部近场区与外部远场区.内部区域为半径c的圆,远场边界同样为圆形,距翼型30倍弦长.选择雷诺数为3×105,对应来流速度为17.5m/s,介质为不可压缩空气,边界条件分别为速度入口、压力出口,出口相对压力为0Pa、翼型表面为无滑移壁面、内部流场和外流场通过Interface进行数据传递.采用基于压力的隐式耦合求解器、Coupled算法,各物理量选择二阶离散.

|
图 3 计算域及边界条件 Fig. 3 Computational domain and boundary conditions |
图 4为计算域网格.远场区为结构网格,近场区为非结构网格.所有流体域全部采用ICEM划分的结构化网格.整体流域的网格数约120 000,为便于湍流模型捕捉边界层流动,翼型表面第一层网格高度设为0.000 01 m,对应y+值约为1.

|
图 4 计算域网格 Fig. 4 The mesh in computational domain |
选取攻角为14°与18°进行验证.由图 5可知,网格由8万增大到10万时,两个攻角下的升力系数值均有增大,可知此时网格并未达到要求.网格由12万增大到14万时,升力系数变化不大,此时,12万网格可满足计算要求,因此,本文采用网格量为12万的网格进行计算.

|
图 5 升力系数随网格数量的变化 Fig. 5 The change of lift coefficient with grid number |
为验证本文计算的可靠性,选取SST k-ω模型、分离涡模型(DES)求解方法和性能并与实验值[16]比较.
DES数值计算时,近壁区的RANS方法选用的湍流模型为SST k-ω模型;LES计算时,对湍流大尺度涡直接求解,小尺度涡采用Smagorinsky-Lily亚格子模型.计算均采用二阶精度进行计算,时间步长5×10-5s,时间与空间的离散精度均采用二阶迎风格式.为方便与实验值对比,选择NACA0018原始翼型进行对比验证计算.
图 6为升阻力系数图,从图 6中可以看出3种湍流模型/求解方法所计算出的升阻力曲线趋势与实验值曲线一致,且误差较小,但3种升力系数曲线总体上会略大于实验值曲线,这是因为数值模拟过程中忽略了一些实际问题,如风况的变化等.

|
图 6 升阻力系数 Fig. 6 Lifting drag coefficient |
对NACA0018翼型在0°~20°范围内的升阻力系数进行计算,并与文献[17]中的实验值进行比较,如图 7所示.

|
图 7 计算值与实验值对比 Fig. 7 Comparison between calculated values and experimental values |
由于实验过程中翼型攻角缓慢增大与减小,其升阻力系数在12°~18°之间因流体上表面流体进入湍流且湍流度越来越强大,故存在些许误差,但误差较小且可以反映大体趋势.由对比结果可知,计算值与实验值吻合度较好,升阻力系数变化趋势较为一致.
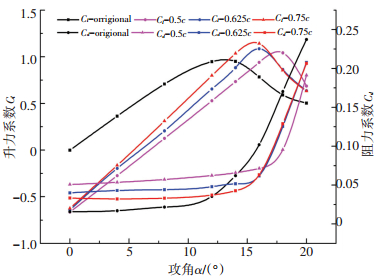
3 结果与分析 3.1 相对位置为研究相对位置对仿生翅片翼气动性能的影响,给定翅片翼的相对长度为0.2c、抬起角度为20°,选取0.5c、0.625c、0.75c三个不同的相对位置研究,图 8为原始翼型和不同位置处翅片翼型升阻力系数.
|
图 8 升阻力系数曲线 Fig. 8 Lift resistance coefficient curve |
从图 8中可发现,升力系数随攻角增大均表现出先增大后减小,但在数值上翅片翼型较原始翼型均有不同程度的增加,且失速角增大.对阻力而言,在低阻区加装翅片翼后阻力增加,攻角增大至原始翼型表面开始出现分离涡时,翅片翼开始发挥作用,随攻角增大,高阻力区效果有体现, 但阻力的数量级较小,变化不大.
小攻角时,原始翼型吸力面流体附着流动,此时加装翅片翼后,翅片翼对流体产生阻挡作用,迫使流体改变运动方向向上绕流翅片翼,上游流体提前转入湍流,襟翼前表面出现漩涡.升力产生的最主要因素为上下表面压力差,压差减小,故低阻区升力降低,翅片翼的阻挡作用导致阻力增大.在高阻力区翅片翼效果明显,因大攻角下原始翼型失速,且随失速程度加深,分离点逐渐向前缘移动.翅片翼可将分离涡分割,并阻挡分离涡继续向前发展.位置不同所导致升力提升效果存在差异,其原因在于,在轻度失速时,分离涡主要位于翼型的尾缘,随着分离点迁移,接近尾缘部位的翅片翼最先对分离层发挥作用,靠近前缘部位的翅片翼依旧是反作用.大攻角时,随着失速程度的增加,分离层逐渐加厚,靠近前缘的翅片襟翼效果较好.当分离点到达靠近前缘的翅片翼的铰点位置时,靠近尾缘的翅片翼所能影响的分离层所占比例很小,分离涡中的流体会越过襟翼向前迁移,靠近前缘的襟翼则可更好地控制分离涡向前发展,因此靠近前缘的翅片翼在更大的攻角下取得最大升力系数.由此可以得出结论,靠近尾缘的翅片翼对轻、中度失速时的流场效果较好;靠近前缘的翅片翼更适合深度失速状态.
翼型绕流的阻力可分为由于流体黏性所引起的摩擦阻力和压差阻力以及尾缘涡所产生的诱导阻力.小攻角时原始翼型为附着流,阻力主要为摩擦阻力.加装固定角度翅片翼,上游流体提前转入湍流,并附有分离涡产生,此时压差阻力及诱导阻力增大,此为小攻角时阻力增大原因.大攻角时翅片翼将原有大分离涡打散成小的涡团,使涡体积变小且阻止其向前迁移,使得压差阻力和诱导阻力减小,因此大攻角下阻力有所减小.
图 9为相对长度为0.2c、抬起角度为20°,不同位置处翅片翼型的力矩系数随攻角的变化曲线.

|
图 9 襟翼力矩系数变化曲线 Fig. 9 Flap torque coefficient curve |
由图 9可看出,固定角度使得襟翼的力矩系数为在小攻角时为负值,襟翼受负的力矩说明此时的抬起角度过大,可通过减小抬起角度或者增大攻角使襟翼的力矩由负转正.由图 8和9可发现随攻角的增加,力矩系数先增加后减小且与升力系数的趋势相似.靠近尾缘的翅片翼,低阻区域襟翼的力矩系数较大,且先达到最大值,越靠近前缘,力矩系数极值对应的攻角越大.因为随分离涡的产生及发展,靠近尾缘的襟翼最先发生作用,此时靠近前缘的襟翼作用效果比靠近尾缘襟翼差.分离程度加深使靠近前缘的襟翼逐渐发挥作用,靠近后缘的襟翼作用效果变弱.
图 10为相对长度l=0.2c,相对位置d=0.5c、d=0.625c及d=0.75c处加装不同抬起角度的翅片翼在不同攻角下的流场比较.升力系数可知因小攻角时翅片翼的效果不好,其主要作用效果在高攻角时,故此处选取攻角α=16°及α=20°时的翅片翼流场进行对比分析.随攻角从零开始增大,原始翼型吸力面呈现出从附着流动到失速再到深度失速.对比图 10(a)、(b)、(c)可发现,16°攻角时,原始翼型表面已出现较大的分离涡,加装翅片翼之后,均有所改善. 0.5c处的翅片翼虽阻止分离涡的向前发展,但下游区域仍出现较大的分离涡,原因是分离点未到达铰点处,此时的翅片翼主要影响是增加阻力.反而,0.75c处的翅片翼完全将流通从中间分割,并完全阻止分离涡的发展且副涡消失,下游流体具有一定的下洗现象,类似于康达效应,此现象有利于提高升力.当攻角为20°时原始翼型的流场,明显发现分离层变厚变大,分离涡覆盖整个上表面.加装翅片翼之后,分离剪切层内流体流动受到不用程度的干扰. 0.75c处的翅片翼虽对流场进行分割,但其所影响的区域仅占分离层很小的比例,翅片翼末端上方的分离层绕过翅片翼向前发展;0.5c处的翅片翼将分离层完全分割成前后两部分,大涡变小涡,且涡团变小,影响区域变小.印证图 8的结论,大攻角时深度失速时,靠近前缘的翅片翼效果较好,中度失速时靠近尾缘的翅片翼收益更高.效果较好的翅片翼压强分布存在共同点:翅片翼上表面的压强从尾部到根部逐渐减小,效果最好时的宏观表现是翅片翼的末端刚好接触分离层的上边缘;翅片翼上下表面压力出现分界线,且下表面压力大于上表面压力.

|
图 10 不同位置处仿生翅片翼的压力云图及流线图 Fig. 10 Pressure cloud diagram and streamline diagram of fin wing at different positions |
由于相对位置对翅片翼气动特性的影响,得出翅片翼的作用与分离点和铰点的相对位置有关,经相对位置的研究可知,在小攻角范围内,翅片翼会使翼型升力减小阻力增大,故主要指针对高阻力区的作用进行分析. 图 11为0.75c处,抬起角度θ=20°时不同长度翅片襟翼翼型的升阻力系数随攻角的变化趋势.
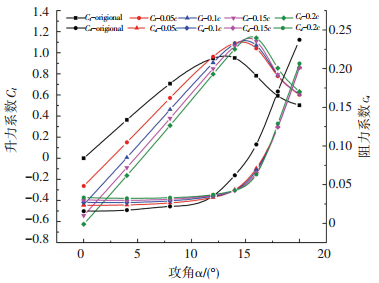
|
图 11 不同长度翅片翼升阻力系数 Fig. 11 Wing lift coefficient of fins of different lengths |
由图 11可看出,随相对长度的增加最大升力系数CLmax依次递增,零升力角增大.因为翼型从失速开始到深度失速的过程中,分离层加厚,若保持长度不变则翅片翼的作用效果及对分离层的影响区域对于分离层的比例越来越微弱,因此,需增加长度以适应流动分离程度的加深.分离层的上边缘从襟翼根部变化到末端的过程,虽翅片翼的控制效果不能够达到最大化但升力系数仍保持上升趋势;随着攻角增大,分离层超出翅片翼末端的距离越来越远,此时的控制效果不佳.这种变化趋势通过升力系数反应出来即为先增大后减小.
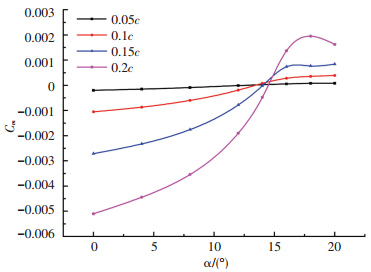
图 12为0.75c处,抬起角度θ=20°时不同长度的翅片翼力矩系数曲线.
|
图 12 襟翼力矩系数变化曲线 Fig. 12 Flap torque coefficient curve |
由图 12曲线可看出,长度对襟翼力矩系数的影响较大.分离涡产生的初始阶段分离层较薄,过长的襟翼导致其末端进入分离层外的区域,此时翅片翼上表面产生附壁现象,襟翼下游的分离涡尺度增大.过长的襟翼长度使襟翼前表面局部压强增大,襟翼产生负的力矩,此时应增大攻角或减小抬起角度,或减小襟翼长度.对比0°~15°攻角内的力矩系数随长度的增加而增大,长度越短,产生负的力矩越小. 14°~15°攻角内, 0.1c和0.15c的翅片翼效果较好,15°之后0.2c的翅片翼效果最佳.
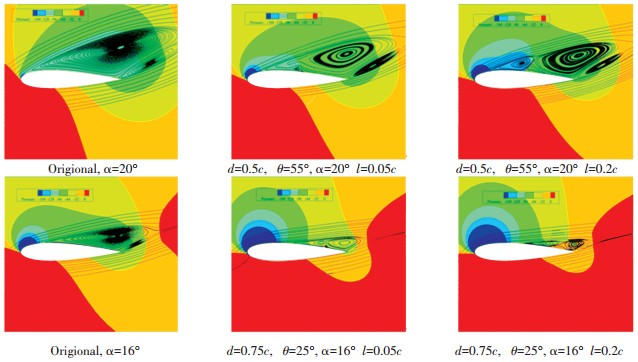
图 13为不同长度翅片翼流场比较.反映出长度不同对流场作用效果的不同. α=20°时原始翼型吸力面为大范围覆盖的一个分离涡,当翅片翼长度为0.05c时,下游区域分离涡中的流体仍可绕过翅片翼向前发展,此时翅片翼的效果十分微弱,但分离涡明显变小.当长度增大至0.2c时,已经可将分离层完全分割成两部分,下游区域的分离涡不能向前迁移,且尾部副涡变小. 0.2c时分离层外部流体流过翅片翼后又轻微的下洗现象,类似于康达效应,有助升力提升.在针对相对位置分析时发生类似的现象,共同之处在于翅片翼末端恰好接触分离层上部边缘或仅有微小偏差,说明此时的角度即为翅片翼作用的最佳角度.
|
图 13 不同长度翅片翼流场比较 Fig. 13 Comparison of fin wing flow field with different lengths |
前面分别研究相对位置和相对长度对仿生翅片翼的影响,发现对相对位置而言,其产生影响是原始翼型的分离点与其铰点相对位置的关系,而影响不同长度的翅片翼作用效果是随着攻角的增大同样增大的分离层厚度. 2个变量并未有相互影响,2变量的同时改变仅会对相同攻角和抬起角度对应的升力的最大值产生影响,因而此处以升力系数的最大值相较于原始翼型的改变量作为衡量标准,研究相对长度和相对位置对最佳控制效果的影响.
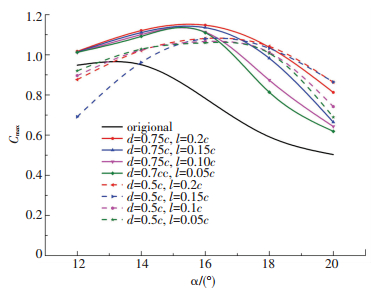
图 14为最大升力系数随攻角变化.由图 14中可以看出,攻角较小(14°,16°)时,0.5c位置处的襟翼对升力系数的提升普遍小于0.75c位置处的襟翼.攻角较大(18°,20°)时,0.5c位置处的襟翼优势较为明显.襟翼位于0.75c时,整体上看,襟翼长度越小,对升力系数的提升越小.攻角18°时例外,长度0.15c的襟翼对升力系数的提升大于长度0.2c的襟翼.襟翼位于0.5c时,整体规律与位于0.75c的襟翼相似.攻角20°例外,此时长度0.15c的襟翼对升力系数的提升大于长度0.2c的襟翼.根据以上结果可知,襟翼位置越靠近翼型前缘,越适于改善大分离流动,越靠近翼型尾缘,越适于改善中度分离流动.
|
图 14 最大升力系数随攻角变化 Fig. 14 Change in maximum lift coefficient with angle of attack |
图 15为最佳襟翼角度随攻角变化.由图 15中可看出,由翼型分离点与襟翼铰点位置的关系,位于0.75c处的襟翼仅当攻角增至14°时才发挥作用,而0.5c处的襟翼攻角增至16°时发挥作用.位置较靠近后缘的襟翼,同攻角下,其最佳襟翼角度普遍大于位置较靠近前缘的襟翼.同位置的襟翼,襟翼长度越小,同攻角下,最佳襟翼角度越大.

|
图 15 最佳角度随攻角变化 Fig. 15 The best angle with the angle of attack changes |
1) 仿生翅片翼的气动性能是由翅片翼的相对位置、相对长度共同决定的,单变量的研究不能够准确地解释其中的规律.
2) 当吸力面发生流动分离且分离点处于翅片翼铰点上游时,翅片翼抬起通过分割分离涡并阻挡分离涡向前缘的迁移,减小分离涡的影响范围.在翅片翼前端形成低压区,对流体实现加速,从而达到流动分离的延缓的效果,此外在最佳角度处还表现出一定的康达效应.
3) 以翅片襟翼的最佳控制效果作为衡量标准,靠近前缘处的翅片襟翼对大分离流动效果显著;靠近尾缘的翅片翼对于中度的流动分离效果较好.相对长度对翅片翼气动性能的影响并非简单的线性关系,且长度过短时无法对分离层产生有效分割,过长时会影响分离层上方的流体.当翅片翼末端刚好接触分离层的边缘时,控制效果最佳.
| [1] |
KROO I. Drag due to lift: concepts for prediction and reduction[J]. Annual Review of Fluid Mechanics, 2001, 33(1): 587. DOI:10.1146/annurev.fluid.33.1.587 |
| [2] |
GLEZER A, AMITAY M. Synthetic jets[J]. Annual Review of Fluid Mechanics, 2002, 34: 503. DOI:10.1146/annurev.fluid.34.090501.094913 |
| [3] |
KIM J, BEWLEY T R. A linear systems approach to flow control[J]. Annu. Rev. Fluid Mech, 2007, 39: 383. DOI:10.1146/annurev.fluid.39.050905.110153 |
| [4] |
CHOI H, JEON W P, KIM J. Control of flow over a bluff body[J]. Annu. Rev. Fluid Mech, 2008, 40: 113. DOI:10.1146/annurev.fluid.39.050905.110149 |
| [5] |
HAO W X, LI C, YE Z, et al. Computational study on wind turbine airfoils based on active control for deformable flaps[J]. Journal of Mechanical Science and Technology, 2017, 31(2): 565. DOI:10.1007/s12206-017-0109-1 |
| [6] |
NICKERSON J. A study of vortex generators at low Reynolds numbers[R]. AIAA-86-0155, 1986.
|
| [7] |
GOGRAVE, BRAMESFELD T, MAUGHMER M D. Experimental investigation of self-actuating, upper-surface, high-lift-enhancing effectors[J]. Journal of Aircraft, 2015, 39(1): 120. |
| [8] |
GRAHAM R R. The Silent Flight of Owls[J]. Aeronautical Journal, 1934, 38(286): 837. |
| [9] |
LILLEYG M.A study of the silent flight of the owl[R]. AIAA Paper 1 998 -2 340, 1998.
|
| [10] |
GEYER T, SARRADJ E, FRITZSCHE C. Measurement of the noise generation at the trailing edge of porous airfoils[J]. Experiments in Fluids, 2010, 48(2): 291. DOI:10.1007/s00348-009-0739-x |
| [11] |
刘博, 姜鹏, 李旭朝, 等. 鲨鱼盾鳞肋条结构的减阻仿生研究进展[J]. 材料导报, 2008, 22(7): 14. LIU Bo, JIANG Peng, LI Xuzhao, et al. Drag-reduction bionic research on riblet surfaces of shark skin[J]. Materials Review, 2008, 22(7): 14. DOI:10.3321/j.issn:1005-023X.2008.07.004 |
| [12] |
张学迅.锯齿尾缘叶片空气动力特性的数值模拟研究[D].北京: 中国科学院研究生院工程热物理研究所, 2013. ZHANG Xuexun. Numerical simulation of aerodynamic characteristics of sawtooth blade[D]. Beijing: Institute of Engineering Thermophysics, Graduate School of the Chinese Academy of Sciences, 2013 |
| [13] |
姜琬, 贾重任, 卢芳春.仿生系列跨介质新概念飞行器气水动布局设计[C]//中国航空学会青年科技论坛.北京: 中国航空学会, 2014. JIANG Wan, JIA Chongren, LU Fangchun.Bionics series air-water layout design for new concept aircraft with cross-media[C]//China Academy of Aeronautical Youth Technology Forum.Beijing: China Academy of Aeronautical, 2014. |
| [14] |
SCHLUTER J U. Lift enhancement at low reynolds numbers using self-activated movable flaps[J]. Journal of Aircraft, 2010, 47(1): 348. DOI:10.2514/1.46425 |
| [15] |
廖庚华.长耳鸮翅膀气动与声学特性及其仿生应用研究[D].长春: 吉林大学, 2013. LIAO Genghua. Study on aerodynamic and acoustic characteristics of long-eared wings and its bionic application[D]. Changchun: Jilin University, 2013. |
| [16] |
TIMMER W A. Two-dimensional low-reynolds number wind tunnel results for airfoil NACA 0018[J]. Wind Engineering, 2008, 32(6): 525. DOI:10.1260/030952408787548848 |
| [17] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598. DOI:10.2514/3.12149 |
 2019, Vol. 51
2019, Vol. 51


