近20年来,仿真计算技术迅速发展,很多工程实际问题的计算量可通过试验设计的方法进行控制.传统试验设计包括正交设计、均匀试验设计(UD)[1]、拉丁超立方设计(LHS)[2]、最优拉丁超立方设计(OLH)[3]等.这些方法都一次性给定试验点数目,使试验点对设计空间有较好的填充特性.但这些方法没有考虑目标函数特性,不同设计问题,对试验点的分布要求不同,不能一概而论.此外,这些方法都一次性固定试验点数量,加点或者取点不足将不能满足其取点规则.
为解决上述问题,利用Kriging模型[4]不仅能给出对目标函数的预估值,还能给出预估值的理论误差及其分布情况的独特优势. Jones等人提出的基于Kriging模型和期望值改进准则的有效全局优化(EGO)算法[5-6]已在航空航天[7-8]、结构优化[9-10]等领域广泛应用.将基于“加点准则优化”的Kriging序贯设计[11]引入到动静压滑动轴承[12]优化设计问题中,利用已有函数信息进一步优化试验点的布局,细化研究目标函数的优选区域并兼顾非优选区域已建立函数的精确度,用以提高轴承的综合性能、降低其摩擦功耗,从而提升旋转机械的传动效率.
旋转机械高效、稳定运转的首要问题之一是处理好承载能力和摩擦功耗之间的关系.单位承载力下摩擦功耗能有效反映这项设计指标,常被作为滑动轴承设计的优化目标.然而,传统优化方法[13]需要大样本的仿真模拟导致优化效果不甚理想.构建考虑几何结构影响的单位承载力下摩擦功耗的单目标优化模型.利用序贯设计的优势,更加有效地发挥试验点对于优化设计的指导作用[14].通过优化加点获取有代表性的样本点并选择新训练样本点进行迭代求解,以提高模型代理精度.最终快速准确获取全局最优解的Kriging模型.
1 Kriging代理模型介绍Kriging方法是一种基于统计学理论的插值方法,其模型包含均值项和随机项.前者为回归函数,后者为符合一定预设统计学规律的随机变量,即
| $ \hat{y}(x)=\boldsymbol{F}^{\mathrm{T}}(x) \beta+z(x). $ |
式中:
随机项的函数模型可以通过事先预设的数据间的相关函数模型来确定.采样点的协方差如下所示:
| $ E[z(\boldsymbol{w}) z(\boldsymbol{x})]=\sigma^{2} \boldsymbol{R}\left(\theta, \boldsymbol{w}_{j}, \boldsymbol{x}_{j}\right). $ |
式中R(θ, wj, xj)为样本点wj,xj之间的相关函数,工程中通常选用高斯相关函数
| $ \boldsymbol{R}\left(\theta, \boldsymbol{w}_{j}-\boldsymbol{x}_{j}\right)=\prod\limits_{j=1}^{n} \exp \left(-\theta\left(\boldsymbol{w}_{j}-\boldsymbol{x}_{j}\right)^{2}\right). $ |
式中θ是高斯相关函数的关键参数,通过优化θ,调节设计点的相关性.
给定m个设计点X=[x1,
| $ \hat{y}(\boldsymbol{x})=\boldsymbol{c}^{\mathrm{T}} \boldsymbol{Y}=\boldsymbol{F}^{\mathrm{T}}(\boldsymbol{x}) \hat{\boldsymbol{\beta}}+\boldsymbol{r}^{\mathrm{T}}(\boldsymbol{x}) \boldsymbol{R}^{-1}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}}). $ |
式中:
| $ \hat{\beta}=\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Y}, $ |
| $ \sigma^{2}=\frac{1}{m}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}})^{\mathrm{T}} \boldsymbol{R}^{-1}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}}). $ |
此外,R是相关矩阵,其表达式为
| $ \boldsymbol{R}=\left[\begin{array}{ccc}{\boldsymbol{R}\left(\boldsymbol{w}_{1}, \boldsymbol{x}_{1}\right)} & {\cdots} & {\boldsymbol{R}\left(\boldsymbol{w}_{1}, \boldsymbol{x}_{n}\right)} \\ {\vdots} & {\ddots} & {\vdots} \\ {\boldsymbol{R}\left(\boldsymbol{w}_{n}, \boldsymbol{x}_{1}\right)} & {\cdots} & {\boldsymbol{R}\left(\boldsymbol{w}_{n}, \boldsymbol{x}_{n}\right)}\end{array}\right]. $ |
而rT(x)是随机模型相关系数矩阵,表示样本点与预测点之间的相关性,可以表示为
| $ \boldsymbol{r}^{\mathrm{T}}(\boldsymbol{x})=\left(\boldsymbol{R}\left(\boldsymbol{w}_{1}, \boldsymbol{x}_{1}\right), \boldsymbol{R}\left(\boldsymbol{w}_{2}, \boldsymbol{x}_{1}\right), \ldots, \boldsymbol{R}\left(\boldsymbol{w}_{n}, \boldsymbol{x}_{1}\right),\right)^{\mathrm{T}}. $ |
Kriging模型预估计值的均方差为
| $ {\rm{MSE}}\left\{ {\hat y\left( \mathit{\boldsymbol{x}} \right)} \right\} = {\sigma ^2}\left\{ {1 - {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}} + {{\left( {1 - {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}}} \right)}^2}/{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{F}}} \right\}. $ | (1) |
相关参数θ通过最大似然估计计算得到:
| $ \psi \left( \theta \right) = - \frac{{m\ln \left( {{{\hat \sigma }^2}} \right)}}{2} - \frac{{\ln \left| \mathit{\boldsymbol{R}} \right|}}{2}. $ |
通过求解ψ(θ)函数的极大值可得到最优θ值,使得Kriging模型达到最佳精度.
2 基于序贯设计的模型训练本文采用试验设计以提高Kriging全局代理精度和寻找全局最优点,其核心在于新训练样本点的选择以及Kriging模型收敛判据的确定.序贯设计具体步骤如下:
1) 根据工程优化设计要求,确定研究对象并建立相应数学模型、约束条件,并确认设计变量及取值范围.
2) 初始样本选取.通过OLH获取能较好反映设计空间的空间特性的初始样本,并数值求解得到对应的响应,从而得到Kriging模型的启动样本.
3) 建立代理模型.选择二次回归函数和高斯相关函数,并根据步骤2)获取的初始样本集,运用DACE工具箱[15]构建初始Kriging代理模型.
4) 加点准则.通过选择合理的加点法则循环选择新增训练样本点进行迭代求解,用以提高Kriging模型精度.
5) 收敛判定.根据代理模型精度(最优点附近的相对误差)作为收敛准则.如果模型满足收敛条件,则代理模型满足精度要求,建模过程即终止,可以基于模型进入优化阶段.否则进入下一次循环返回步骤4).
2.1 加点准则建立代理模型后,通过一定加点法则选择新的样本点.基于Kriging模型的算法[16]中常用的加点准则包括改善期望准则[17](EI)、均方差准则[18](MSE)和最小化代理模型预测准则(MSP)等.
MSE准则是直接运用Kriging代理模型提供的均方差估计(式(1))最大处作为新样本点的位置.该方法对提高模型全局精度,避免优化结果收敛于局部最优有较好的效果,但收敛的速度偏慢.
EI准则是综合考虑预测值以及方差加权的一种高效全局优化(EGO)方法.设当前最优点响应值为Ymin,且Kriging代理模型预测值满足均值
| $ P\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{{\sqrt {2\pi } \sigma \left( \mathit{\boldsymbol{x}} \right)}}\exp \left[ { - \frac{{{{\left( {{Y_{\min }} - I - \hat y\left( \mathit{\boldsymbol{x}} \right)} \right)}^2}}}{{2{\sigma ^2}\left( \mathit{\boldsymbol{x}} \right)}}} \right]. $ |
针对最小化优化问题,目标函数响应值增量为
| $ I\left( \mathit{\boldsymbol{x}} \right) = {Y_{\min }} - y\left( \mathit{\boldsymbol{x}} \right). $ |
则响应值目标提高的期望值为
| $ \left[ {I\left( \mathit{\boldsymbol{x}} \right)} \right] = \sigma \left( \mathit{\boldsymbol{x}} \right)\left[ {u\mathit{\Phi }\left( u \right) + \varphi \left( u \right)} \right], $ |
| $ u = \frac{{{Y_{\min }} - \hat y\left( \mathit{\boldsymbol{x}} \right)}}{{\sigma \left( \mathit{\boldsymbol{x}} \right)}}. $ |
式中:Φ和
通过计算目标函数改善的期望,把期望最大值点作为新训练样本点,从而寻找全局最优解的优化方法.该方法有助于提高优化的局部精度,在全局最优点所在区域确定的前提下,这种方法可提高优化结果的精度.
综合考虑模型精度和优化结果的精度,以及单独使用一种加点准则收敛速度较慢、效率不高的缺点, 使用“MSE+EI”结合的“并行加点准则[8]”,即一次优化迭代增加2个样本点.不仅可以保证代理模型全局精度,还可以更有效逼近全局最优解.
2.2 收敛判定根据代理模型在最优点附近的相对误差作为优化终止的收敛条件:
| $ \left| {\hat f\left( {{x_k}} \right) - f\left( {{x_k}} \right)} \right| \le {\varepsilon ^ * }f\left( {{x_k}} \right). $ | (2) |
式中:k为优化迭代次数;
使用2个经典的优化测试函数(六峰值驼背函数和Rosenbrock函数),对LHS、OLH以及均匀设计和优化加点后的Kriging模型的全局精度以及寻优结果进行比较.
3.1 测试函数六峰值驼背函数(Six-Hump Camel Back function):
| $ f\left( {{x_1},{x_2}} \right) = x_1^2\left( {4 - 2.1x_1^2 + \frac{{x_1^4}}{3}} \right) + {x_1}{x_2} + x_2^2\left( { - 4 + 4x_2^2} \right). $ |
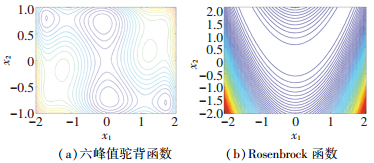
图 1(a)为六峰值驼背函数等值线图,此函数由一个四阶和一个六阶的一维多项式函数联立而成,并含有二阶混合项. 2个全局最优点:(0.0898,-0.7127)和(-0.0898 0.7127),4个局部最优点,最小响应值fmin=-1.029 8.
|
图 1 测试函数等值线图 Fig. 1 Test function contour map |
Rosenbrock函数:
| $ f\left( {{x_1},{x_2}} \right) = {\left( {1 - {x_1}} \right)^2} + 100{\left( {{x_2} - x_1^2} \right)^2}. $ |
与六峰值驼背函数等值线图不同,Rosenbrock函数图像如图 1(b)关于x1=0并不对称.此函数仅有一个全局最优点,位于(1, 1),对应响应值fmin=0,全局最优点位于一个近似抛物线形的梯度值极小的“深谷”中.此函数对于检验优化算法的寻优效率有很好的效果.
3.2 方案评价标准采用均方根误差对不同试验设计方案下建立的Kriging代理模型进行全局误差分析.将二维设计空间等分为n×n的网格,选取网格节点为待测点,并建立如下形式的均方根误差模型评价代理模型误差:
| $ {\rm{RMSE}} = \sqrt {\sum\limits_{i = 1}^{{n_t}} {{{\left( {{e^{\left( i \right)}}} \right)}^2}/{n_i}} } ,{e^{\left( i \right)}} = \left\| {\left( {\hat y_{\rm{t}}^{\left( i \right)} - y_{\rm{t}}^{\left( i \right)}} \right)} \right\|. $ | (3) |
式中:nt为检测样本点的个数,
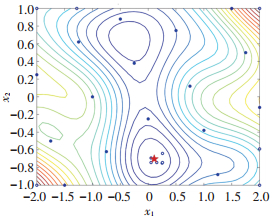
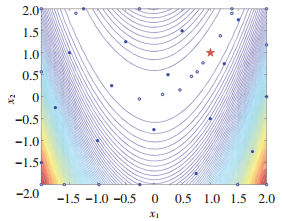
在测试函数建模过程中,只改变试验设计方法,而样本点数、加点准则以及误差分析方法均保持一致.首先利用DACE工具箱进行初始Kriging建模,再使用“并行加点准则”不断更新训练样本点优化模型,当代理模型满足收敛条件(式(2))时,试验设计加点后样本点分布情况如图 2、图 3所示,其中,“实心圆”点表示初始样本点,“空心圆”点表示通过“并行加点准则”新添加的样本点,“五角星”表示实际全局最优点.
|
图 2 六峰值驼背函数序贯设计样本点分布情况 Fig. 2 Sample distribution of sequential design for Six-Hump Camel Back function |
|
图 3 Rosenbrock函数序贯设计样本点分布情况 Fig. 3 Sample distribution of sequential design for Rosenbrock function |
2个测试函数均采用OLH设计构建初始点集,采用并行加点准则增加新样本点,直到代理模型收敛.利用式(3)评价各测试函数下模型精度,结果如表 1、2所示.
| 表 1 各试验设计方案Kriging模型均方根误差汇总表(六峰值驼背函数) Tab. 1 RMSE of Kriging model for different DoE methods(Six-Hump Camel Back function) |
| 表 2 各试验设计方案Kriging模型均方根误差汇总表(Rosenbrock函数) Tab. 2 RMSE of Kriging model for different DoE methods(Rosenbrock function) |
分析表 1可知,初始样本采用OLH方案,因此,二者有相同的误差.由表 1中误差数据可知,虽然在增加4个点后,相对于OLH设计,序贯设计的误差有所升高,这种现象可能的原因是测试函数波动较大,在梯度较大的区域需要多个设计点来捕捉函数值的变化,导致某些增加的试验点距离较近,进而改变了相关矩阵R的条件数,影响矩阵求逆运算的精度,最终导致模型精度有一定程度降低.但随着继续加点,模型精度则明显提高,而增至29点时,相对于其他设计的优势可明显体现出来.而OLH和均匀设计的模型精度变化规律类似,随着点数增加,精度略微改善.相较之下,并行加点准则由于考虑了函数对于自变量的响应特性,加点位置更加有针对性,对于模型精度的提高更有效. LHS、OLH和均匀设计的模型精度变化规律类似,随着点数增加精度有所改善,但改善程度有限.
而Rosenbrock函数同六峰值驼背函数的显著不同是函数值变化平缓,梯度值小,特别是最优点所在区域位于一个梯度极小的谷中,因此序贯设计所增加的点的分布相对较均匀,有利于相关矩阵的运算,从空间相关性上更有利于捕捉函数的全局特性.由表 2可知,样本点数由17增加到37个时,模型精度呈线性升高的趋势,序贯设计的精度明显优于其它设计方案.
当Kriging代理模型满足收敛条件时,比较4种设计方法下代理模型预测全局最优解能力,结果如表 3、4所示.对于六峰值驼背函数,基于LHS设计的模型全局最优解距离真实最优解较远,而基于OLH、均匀设计和序贯设计的模型预测的全局最优点位置接近,后3种设计中,序贯设计预测最优点对应的响应值更接近真实最优解.对于Rosenbrock函数可得类似的结论.
| 表 3 各试验设计方案Kriging模型全局最优解汇总表(六峰值驼背函数) Tab. 3 Global optimal solution of Kriging model for different DoE methods(Six-Hump Camel Back function) |
| 表 4 各试验设计方案Kriging模型全局最优解汇总表(Rosenbrock函数) Tab. 4 Global optimal solution of Kriging model for different DoE methods(Rosenbrock function) |
综合分析得,序贯设计考虑设计空间的空间填充特性以及目标函数的函数特性,加点位置更加有针对性,对模型精度的提高更有效.所以序贯设计的模型误差降低速度明显高于传统试验设计.由各试验设计方案的模型全局最优解情况可知,序贯设计有更好地收敛到优化问题的真实最优解的能力.这是由于使用“并行加点准则”克服了寻优算法容易陷入局部最优的缺点,改善了对设计空间搜索的全局性.
4 动静压滑动轴承优化设计随着滑动轴承的应用范围不断向着高速、重载方向发展,需要处理好轴承承载能力和摩擦功耗之间的关系.轴承的摩擦功耗不仅带来能量损失,其导致的润滑油温度增加直接影响润滑油粘度,大大降低轴承的综合性能.当前滑动轴承领域中常采用随机方向搜索法、复合形法等常规优化方法对轴承结构尺寸进行优化设计.根据以上比较分析结果,本文将基于Kriging代理模型的序贯设计方法引进到滑动轴承的优化设计中.选取动静压轴承单位承载力下摩擦功耗最小为目标函数进行优化,并同传统复合形法优化结果进行比较.
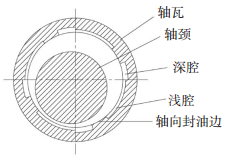
以圆柱动静压轴承(见图 4)为研究对象,对其几何结构参数进行序贯设计优化,其中轴承重要参数为:主轴转速为10 000 r/min、腔数为4个、偏心率为0.25、直径为70 mm、深腔包角为15°、浅腔深度0.022 mm、深腔深度0.25 mm、半径间隙0.03 mm.选择以单位承载力下的摩擦功耗最小为目标函数,设计变量取长径比l/d、轴向两侧封油边宽度z1, z2和浅腔包角θq.分别建立了相同工况条件下基于序贯设计和基于OLH设计的Kriging代理模型并与复合形法进行对比分析.
| $ \min F\left( x \right) = \left( {\frac{{{{\bar H}_f} + {{\bar H}_p}}}{{{{\bar F}_r}}}} \right). $ |
|
图 4 带深浅腔的圆柱动静压滑动轴承 Fig. 4 Cylindrical hybrid bearing with deep and shallow pocket |
式中:F(x)为目标函数;Hf为无量纲摩擦功耗;Hp为无量纲泵功耗;Fr为无量纲承载力.
| $ {\rm{s}}.\;{\rm{t}}.\left\{ \begin{array}{l} l/d \in \left[ {0.5,0.8} \right]\\ {z_1},{z_2} \in \left[ {1,7} \right]\\ {\theta _q} \in \left[ {44,53} \right] \end{array} \right.. $ |
式中:l/d为长径比;z1, z2为轴向两侧封油边宽度(mm);θq为浅腔包角(°).
浅腔包角和封油面的大小决定动压效应的作用区域,区域越大,承载力越大,摩擦功耗也越大.而长径比的大小决定了轴承侧流量,进而影响摩擦功耗.轴承长径比对轴承性能有较大影响,一般为了提高运行稳定性和减少轴承尺寸,且使摩擦阻力减小、温升下降,取用较小值.但若取值过小,将造成轴承的承载能力迅速下降等不良后果.然而,这些参数对设计目标的影响不可单一而论,各参数的耦合效应难以直观地从物理意义上进行分析,基于代理模型的优化设计有助于设计空间的全局性寻优.
由不同试验设计方案对代理模型精度的影响分析,OLH设计和均匀设计的模型精度优于LHS设计方案的模型.在此选择OLH设计和Kriging序贯设计进行比较.
首先,采用OLH方法选取25个初始样本点,并采用Kriging“并行加点准则”(EI+MSE准则),建立基于序贯设计的代理模型.此过程中设计变量及每组设计变量对应的目标函数真实值变化如表 5所示.
| 表 5 Kriging序贯设计建模计算过程 Tab. 5 Kriging modeling process based on sequential design |
比较Kriging模型在最优点处的预测函数值与精确数值计算结果,随着样本点数增加,代理模型在最优点处的误差不断减小,经9次迭代,当样本点数增加至43时,Kriging代理模型在最优点处的相对误差ε*达到8.7×10-4.
按照OLH试验设计准则给出样本点数同为43的试验设计方案,并基于这些点的数值计算结果建立代理模型,求得此模型的最优点.采用复合形法初始样本点为4个,在经过39次迭代共计43个样本点情况下得到最优点.与Kriging序贯设计所建立的模型最优点对比见表 6.
| 表 6 不同试验设计方案动静压轴承的优化结果对比 Tab. 6 Comparison of optimization results of Hybrid Bearing with different DoE methods |
对比OLH试验设计、Kriging序贯设计和复合形法的最优点参数值和对应的精确数值计算结果, 在样本点数相同的情况下,Kriging序贯设计所建立的模型能够找到更好的设计结果,相对基于OLH设计的优化结果,目标函数即单位承载力下的摩擦功耗降低了2.33%.在相同的样本点数的情况下,Kriging序贯设计相对于复合形优化方法目标函数降低了4.22%.由于模型预测的时间较短,相对于样本点仿真计算的时间几乎可忽略,因此可近似认为,样本点数正比于寻优时间的长短,可直接用于衡量寻优效率.相对于传统一次成型的试验设计以及传统优化方法,序贯试验设计能提高模型的全局精度,进而直接提高模型的寻优效率.
5 结论采用并行加点准则及相应收敛条件构建基于Kriging序贯设计的代理模型,与基于传统试验设计的模型进行比对.通过测试函数和动静压轴承的工程应用,验证了Kriging序贯设计的先进性和可靠性,揭示了序贯优化设计能有效利用设计空间的空间填充特性和目标函数的函数特性,进而提高了模型的全局和局部精度,有效缩短了基于高精度数值计算的优化设计周期.
| [1] |
FANG K T, LIN D K J, WINKER P, et al. Uniform design: theory and application[J]. Technometrics, 2000, 42(3): 237. DOI:10.1080/00401706.2000.10486045 |
| [2] |
GIUNTA A, WOJTKIEWICZ S, ELDRED M. Overview of modern design of experiments methods for computational simulations[C]//41st Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2003: 649.
|
| [3] |
ZHAO L, CHOI K, LEE I. A metamodeling method using dynamic kriging and sequential sampling[C]//13thAIAA/ISSMO Multidisciplinary Analysis Optimization Conference.Fort Worth: AIAA, 2010: 9391.
|
| [4] |
KLEIJNEN J P C. Design and analysis of simulation experiments[C]//International Workshop on Simulation. Springer, Cham, 2015: 3
|
| [5] |
孙志礼, 李瑞, 闫玉涛, 等. 一种用于结构可靠性分析的Kriging学习函数[J]. 哈尔滨工业大学学报, 2017, 49(07): 146. SUN Zhili, LI Rui, YAN Yutao, et al. A Kriging based learning function for chemical reliability analysis[J]. Journal of Harbin Institute of Technology, 2017, 49(07): 146. DOI:10.11918/j.issn.0367-6234.201604121 |
| [6] |
JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455. DOI:10.1023/A:1008306431147 |
| [7] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197. HAN Zhonghua. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(11): 3197. DOI:10.7527/S1000-6893.2016.0083 |
| [8] |
韩少强, 宋文萍, 韩忠华, 等. 基于梯度增强型Kriging模型的气动反设计方法[J]. 航空学报, 2017, 38(07): 138. HAN Shaoqiang, SONG Wenping, HAN Zhonghua, et al. Aerodynamic inverse design method based on gradient-enhanced Kriging model[J]. Acta Aeronautica ET Astronautica Sinica, 2017, 38(07): 138. DOI:10.7527/S1000-6893.2016.0299 |
| [9] |
李小刚, 程锦, 刘振宇, 等. 基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J]. 机械工程学报, 2014, 50(03): 165. LI Xiaogang, CHENG Jin, LIU Zhenyu, et al. Robustoptimization for dynamic characteristics of mechanical structures based on double renewal Kriging model[J]. Journal of Mechanical Engineering, 2014, 50(03): 1653. DOI:10.3901/JME.2014.03.165 |
| [10] |
张宇, 覃刚, 张云清, 等. 基于克里金元模型的离心泵水力性能多目标优化[J]. 华中科技大学学报(自然科学版), 2015, 43(04): 54. ZHANG Yu, ZHAO Gang, ZHANG Yunqing, et al. Kriging based multi-objective optimization for hydraulic performance of centrifugal pump[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(04): 54. DOI:10.13245/j.hust.150411 |
| [11] |
HUANG D, ALLEN T T, NOTZ W I. Sequential Kriging optimization using multiple-fidelity evaluations[J]. Structural and Multidisciplinary Optimization, 2006, 32(5): 369. DOI:10.1007/s00158-005-0587-0 |
| [12] |
郭红, 岑少起, 张绍林.圆柱、圆锥动静压滑动轴承设计[D].郑州: 郑州大学, 2013: 260 GUO Hong, CEN Shaoqi, ZHANG Shaolin. Cylindrical and conical hydrostatic sliding bearing design[D]. Zhengzhou: Zhengzhou University, 2013: 260 |
| [13] |
王丹丹.独立供油径推浮环轴承性能优化分析与软件包开发[D].郑州: 郑州大学, 2010. WANG Dandan. Perormance optimization analysis of the journal-thrust floating ring bearing with independent oil supply and software development[D]. Zhengzhou: Zhengzhou University, 2010. |
| [14] |
ZHANG Z, DEMORY B, HENNER M, et al. Space infill study of Kriging meta-model for multi-objective optimization of an engine cooling fan[C]//ASME Turbo Expo 2014 : Turbine Technical Conference and Exposition. 2014. DOI: 10.1115/GT2014-25281
|
| [15] |
LOPHAVEN S N, NIELSEN H B, SØNDERGAARD J. DACE: a matlab kriging toolbox[M]. IMM, Informatics and Mathematical Modelling, The Technical University of Denmark, 2002.
|
| [16] |
FORRESTER A I J, SOBESTER A, KEANE A J. Engineering design via surrogate modelling: a practical guide[M]. Wiley, 2008.
|
| [17] |
高月华, 王希诚. 基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学, 2012, 29(4): 90. GAO Yuehua, WANG Xicheng. A sequential optimization method with mult-point sampling criterion based on Kriging surrogate model[J]. Engineering Mechanics, 2012, 29(4): 90. |
| [18] |
黄章俊, 王成恩. 基于Kriging模型的涡轮盘优化设计方法[J]. 计算机集成制造系统, 2010, 16(5): 905. HUANG Zhangjun, WANG Chengen. Turbine discs optimization design based on Kriging model[J]. Computer Integrated Manufacturing Systems, 2010, 16(5): 905. DOI:10.13196/j.cims.2010.05.11.huangzhj.007 |
 2019, Vol. 51
2019, Vol. 51



