避障是冗余机械臂路径规划的基本问题之一,是科学和工程领域中的研究热点[1].串联型冗余机械臂的雅克比矩阵为欠约束形式,其运动学逆解存在无穷多个,也可能存在奇异点[2-3],单独依靠逆运动学求解算法难以满足避障要求.目前冗余机械臂避障的常用算法主要包括改进逆运动学求解法[4-6]、自由空间法[7]、遗传算法[8]、A*算法[9]、人工势场法[10-11]等.文献[4-6]对冗余机械臂逆运动学求解算法进行改进,提高求解精度和速度,但仍旧无法有效解决奇异点问题.文献[7]提出基于工作空间密度的平面冗余机械臂避障算法,在生成的工作空间中计算出多个离散解,并将工作空间密度作为评价准则求取最优解.该方法对于处理多障碍物条件下的避障十分有效,但只适用于平面冗余机械臂.
人工势场法在目标点处构建引力势场,障碍物处构建斥力势场,并在两类势场共同作用下,引导机械臂避开障碍物到达目标点[10].它不需要进行逆运动学求解即可完成避障,具有模型简单、算法高效、适应性强的特点,但容易陷入局部极小且难以逃离[12].串联型冗余机械臂在给定末端位姿情况下,有无数组关节角度与之对应[13-14],而传统人工势场法只在笛卡尔空间中对末端建立势场,难以约束各关节位姿.文献[15]提出通过遗传算法求解关节值,利用人工势场法在关节空间内搜索,在极小点处添加虚拟障碍物处理局部极小问题,该方法应用于非冗余机械臂具有一定效果,但不适用于冗余机械臂.文献[16]提出基于构型的人工势场法,与空间机械臂逆运动学求解相结合进行运动规划,该方法在避障方面具有一定成效,但避障结果误差较大,无法约束关节位姿,在冗余机械臂上应用较为困难.
为此,本文提出改进人工势场法,以七自由度冗余机械臂为例建立其运动学模型和碰撞检测模型,分别在笛卡尔和关节空间内建立势场共同引导机械臂运动,在关节空间内求解虚拟目标角度并建立虚拟引力势场处理局部极小问题,仿真和实验对算法有效性进行验证.
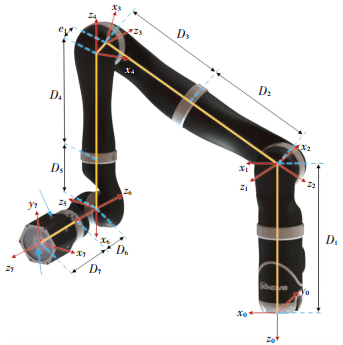
1 机械臂模型 1.1 运动学模型本文以加拿大Kinova公司的Jaco2七自由度冗余机械臂为研究对象.采用D-H法建立机械臂运动学模型如图 1所示,D-H参数见表 1.
|
图 1 机械臂D-H模型 Fig. 1 D-H model of the manipulator |
| 表 1 机械臂D-H模型参数 Tab. 1 The D-H parameter of the manipulator |
表 1中:i(i=1, 2, ..., 7)为机械臂关节序号;Qi为i关节角度.为简化表达,分别将cos(θi)、sin (θi)、cos(αi-1)、sin(αi-1)记为cθi、sθi、cαi-1、sαi-1,则机械臂xi-1-zi-1坐标系到xi-zi坐标系的齐次变换矩阵Mi-1可表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_{i - 1}} = {\mathit{\boldsymbol{R}}_{i - 1}}\left( {{\theta _i}} \right){\mathit{\boldsymbol{T}}_{i - 1}}\left( {{d_i}} \right){\mathit{\boldsymbol{T}}_{i - 1}}\left( {{a_{i\;\; - 1}}} \right){\mathit{\boldsymbol{R}}_{i - 1}}\left( {{\alpha _{i - 1}}} \right) = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\theta _i}}&{ - {\rm{c}}{\alpha _{i - 1}}{\rm{s}}{\theta _i}}&{{\rm{s}}{\alpha _{i - 1}}{\rm{s}}{\theta _i}}&{{\alpha _{i - 1}}{\rm{c}}{\theta _i}}\\ {{\rm{s}}{\theta _i}}&{{\rm{c}}{\alpha _{i - 1}}{\rm{c}}{\theta _i}}&{ - {\rm{s}}{\alpha _{i - 1}}{\rm{c}}{\theta _i}}&{{\alpha _{i - 1}}{\rm{s}}{\theta _i}}\\ 0&{{\rm{s}}{\alpha _{i - 1}}}&{{\rm{c}}{\alpha _{i - 1}}}&{{d_i}}\\ 0&0&0&1 \end{array}} \right]. \end{array} $ |
式中:Ri-1(αi-1)代表将xi-1-zi-1坐标系绕xi-1轴旋转αi-1的变换矩阵,Ti-1(αi-1)代表将xi-1-zi-1坐标系沿xi-1轴平移ai-1的变换矩阵,Ti-1(di)代表将xi-1-zi-1坐标系沿zi-1轴平移di的变换矩阵,Ri-1(θi)代表将xi-1-zi-1坐标系绕zi-1轴旋转θi的变换矩阵.
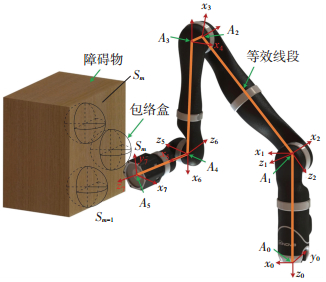
1.2 碰撞检测模型机械臂与障碍物间的碰撞检测采用线段—球体包络盒模型,如图 2所示.根据图 1建立的机械臂D-H模型,共存在6个不重合的坐标系原点,则碰撞检测过程中将连杆i(i=1, 2, ..., 7)组合并等效为5条线段,如图 2中A0A1、A1A2、A2A3、A3A4、A4A5所示,同时对障碍物半径等效增大Rh,Rh为线段Ah-1Ah对应连杆最大半径,h(h=1, 2, ..., 5)为等效线段序号.机械臂末端安装9个测距传感器探测障碍物,如图 1所示,其中沿末端圆周方向均布安装6个传感器,用于探测机械臂末端四周信息,在末端正前方安装3个测距传感器,用于探测机械臂末端正前方朝向信息.机械臂在运动过程中,安装有测距传感器的末端位姿不断变化,则传感器探测方向不断发生改变,通过传感器不断进行障碍物探测,即可获得机械臂各连杆周围的障碍物信息.所探测到的第m(m=1, 2, ..., M)个障碍物表面信息可用空间中一点Pm表示,M为避障完成前探测到的障碍物最大数目.为确保多次探测后球体包络盒将障碍物表面基本包络,需给定球体包络盒的安全半径r,r的取值需同时保证机械臂在避障过程中不影响末端执行器的操作,依据末端执行器及工作环境情况选取.避障过程中机械臂中心线与障碍物间最近距离为Rh+r,当Rh+r取值较小时,机械臂可在较小空间范围内避障,但与障碍物发生碰撞的概率增大,而取值较大时,机械臂与障碍物发生碰撞的概率减小,但避障需要较大空间.障碍物模型可用球体包络盒表示为Sm(Pm, Rh+r),其中Pm为球心,Rh+r为半径.
|
图 2 碰撞检测模型 Fig. 2 Collision detection model |
根据图 2建立的碰撞检测模型,端点Ah与xt-zt(0≤t≤7)坐标系原点重合,此时Ah在xt-zt坐标系中的齐次坐标矩阵为Aht=[0, 0, 0, 1]T,则Ah在x0-z0坐标系中的齐次坐标矩阵为
| $ \mathit{\boldsymbol{A}}_h^0 = \prod\limits_{i = 0}^{t - 1} {{\mathit{\boldsymbol{M}}_i}\mathit{\boldsymbol{A}}_h^t} $ |
针对每条等效线段Ah-1Ah及障碍物的球体包络盒模型Sm(Pm, Rh+r),碰撞检测问题可通过求解球心Pm到线段Ah-1Ah的距离Lmh,并与球体半径Rh+r比较解决.
1) 若Lmh≤Rh+r,则发生碰撞.
2) 若Lmh>Rh+r,则没有发生碰撞.
各条等效线段分别与每个障碍物碰撞检测,即可获得机械臂不发生碰撞条件下的运动空间.
2 改进人工势场法 2.1 势场函数建立在笛卡尔空间内的目标点处建立引力势场Uatt、障碍物处建立斥力势场Urep,在关节空间内的目标位姿处建立引力势场Ujoi,所有势场共同作用引导机械臂向势能减小方向运动.
在笛卡尔空间中建立引力势场函数为
| $ {U_{{\rm{att}}}} = \frac{{{K_{\rm{a}}}}}{2} \times \left( {\left\| {\mathit{\boldsymbol{P}}_{\rm{r}}^0 - \mathit{\boldsymbol{P}}_{\rm{g}}^0} \right\|_2^2 + \left\| {{\mathit{\boldsymbol{\varphi }}_{\rm{r}}} - {\mathit{\boldsymbol{\varphi }}_{\rm{g}}}} \right\|_2^2} \right). $ |
式中:Ka为引力势场参数;Pr0、Pg0分别为当前和目标位姿下末端坐标系原点在基坐标系x0-z0下的坐标向量;
在笛卡尔空间中,障碍物包络盒Sm与线段Ah-1Ah间的斥力势场函数为
| $ {U_{mh}} = \left\{ \begin{array}{l} \frac{{{K_{\rm{r}}}}}{2}{\left[ {\frac{1}{{{L_{mh}} - \left( {{R_h} + r} \right)}} - \frac{1}{{{L_0} - \left( {{R_h} + r} \right)}}} \right]^2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_h} + r < {L_{mh}} < {L_0};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_{mh}} \ge {L_0}. \end{array} \right. $ |
式中:Kr为斥力势场参数;Lmh为障碍物包络盒Sm球心到线段Ah-1Ah的距离;L0为斥力势场作用范围.斥力势场Umh随Lmh减小而增大,当Lmh趋近于Rh+r时,斥力势能迅速增大并趋于无穷,引导机械臂向远离障碍物方向运动.机械臂的总斥力势能为
| $ {U_{{\rm{rep}}}} = \sum\limits_{m = 1}^M {\sum\limits_{h = 1}^H {{U_{mh}}} } . $ |
式中:M为当前保存的障碍物表面位置信息最大数目,H为机械臂等效线段条数.
在关节空间内,建立关节引力势场函数为
| $ {U_{{\rm{joi}}}} = \frac{{{K_{\rm{j}}}}}{2}\sum\limits_{i = 1}^{\rm{I}} {{{\left( {{\gamma _i} - {\theta _i}} \right)}^2}} . $ |
式中:Kj为关节引力势场参数;i(i=1, 2, ..., I)为机械臂关节序号, I=7为关节数目;γi为i关节目标角度;θi为i关节当前角度. Ujoi随γi与θi之间差值增大而增大,引导i关节向γi方向运动.
由于斥力势能太大会影响总势能的下降速度,不利于机械臂向目标位置运动,势场参数Kr、Ka按如下方法调整:
| $ {K_{\rm{r}}} = {K_{\rm{a}}}/MH. $ | (1) |
式中H=5为机械臂等效线段条数.式(1)可保证随障碍物数量增多,斥力势能不会急剧增大.由于关节引力势能太小不利于引导关节到达目标角度,太大不利于引导末端到达目标位姿,势场参数Kj、Ka按如下方法确定:
| $ {K_{\rm{j}}} = {K_{\rm{a}}}/{S_c}I. $ |
式中Sc为常量系数.
假设机械臂在第n步运动前第i个关节角为θin,定义当前关节角集合:Jn={θin, i=1, 2, ..., 7}.机械臂在Jn姿态下,在笛卡尔空间内的引力势能和斥力势能分别记为Uatt(Jn)、Urep(Jn),在关节空间内的引力势能记为Ujoi(Jn),则机械臂的总势能为
| $ {U_{{\rm{tol}}}}\left( {{J_n}} \right) = {U_{{\rm{att}}}}\left( {{J_n}} \right) + {U_{{\rm{rep}}}}\left( {{J_n}} \right) + {U_{{\rm{joi}}}}\left( {{J_n}} \right). $ |
当引力势函数与多个斥力势函数共同作用时,总势能容易陷入局部极小而非全局最小值,不改变势场分布难以引导机械臂继续运动,导致避障任务失败.由于串联型冗余机械臂关节数量较多,当陷入局部极小时,只对末端进行引导难以保证各关节避开障碍物.为此,本文在关节空间内求解虚拟目标角度,同时引导末端和关节运动.
定义机械臂在Jn姿态下的相邻关节角为:Cin={θin+λ0, θin, θin-λ0, i=1, 2, ..., 7},λ0为初始步长.相邻关节角集合为:Cn={Cin, i=1, 2, ..., 7}.若满足Utol(Jn)=min(Utol(Cn)),则判定机械臂陷入局部极小.在关节空间内,虚拟目标角度势函数需在局部极小点处起主要引导作用,并能在逃离局部极小后快速回落至零.机械臂在当前关节角Jn姿态下i关节对应的虚拟目标角度势函数为
| $ {\tilde U_i}\left( {{J_n}} \right) = \frac{{{K_{\rm{v}}}}}{\sigma }{{\rm{e}}^{ - \frac{{{{\left[ {\left( {{{\tilde \gamma }_i} - {\theta _{in}}} \right) - \left( {{{\tilde \gamma }_i} - {\theta _{i1}}} \right)} \right]}^2}}}{{2{\sigma ^2}}}}} - \frac{{{K_{\rm{v}}}}}{\sigma }{{\rm{e}}^{ - \frac{{{{\left( {{{\tilde \gamma }_i} - {\theta _{i1}}} \right)}^2}}}{{2{\sigma ^2}}}}}. $ |
式中:Kv、σ为关节虚拟引力势场参数;
| $ \left\{ \begin{array}{l} \mu - 3\sigma = 0,\\ \mu = \left| {\left. {{{\tilde \gamma }_i} - {\theta _{i1}}} \right)} \right|. \end{array} \right. $ |
解得
| $ \sigma = \left| {{{\tilde \gamma }_i} - {\theta _{i1}}} \right|/3. $ |
机械臂在Jn姿态下具有的虚拟总势能
| $ {\tilde U_{{\rm{tol}}}}\left( {{J_n}} \right) = {U_{{\rm{att}}}}\left( {{J_n}} \right) + {U_{{\rm{rep}}}}\left( {{J_n}} \right) + \sum\limits_{i = 1}^I {{{\tilde U}_i}\left( {{J_n}} \right)} . $ |
为保证Ui能够引导机械臂逃离局部极小,机械臂在Jn姿态下具有的虚拟总势能需大于在Jn+1姿态下具有的虚拟总势能.则Kv需满足
| $ {\tilde U_{{\rm{tol}}}}\left( {{J_n}} \right) > {\tilde U_{{\rm{tol}}}}\left( {{J_{n + 1}}} \right). $ |
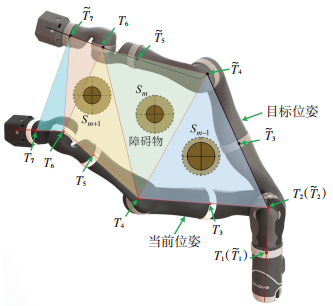
Jaco2机械臂的2、4、6关节控制机械臂在包含等效线段的平面内运动,由于这些关节运动对机械臂等效线段位置影响较大,因此仅对它们求取
| $ {\tilde \gamma _i} = {\tilde \gamma _{iA}} + {\tilde \gamma _{iB}}. $ |
|
图 3 虚拟目标角度求解示意图 Fig. 3 Schematic diagram for solving a virtual target angle |
三角形区域的三个顶点中,若仅存在一个顶点在当前位姿上,则该顶点为活动顶点,以三角形区域T4
改进人工势场法算法主流程如下:
1) 获取机械臂当前位姿的相邻关节角集合Cn,初始步长为λ0.
2) 对Cn中每个相邻关节角组合进行运动学正解,获得各关节点在基坐标系x0-z0下的坐标,求解机械臂等效线段Ah-1Ah方程式和障碍物球体包络盒模型Sm方程式.
3) 将Cn中每个组合对应的各条等效线段Ah-1Ah与所有球体包络盒模型Sm进行碰撞检测,若存在碰撞,将该组合舍弃.
4) 对Cn中每个剩余组合计算总势能,得到总势能最小的一种组合,记为Jmin.
5) 判定机械臂是否陷入局部极小.若陷入局部极小,则进入局部极小处理流程.
6) 判定是否稳定于目标位姿附近,满足条件则更改步长为λ1.
7) 判定是否到达目标位姿或更换步长后仍稳定于目标点附近.满足条件则避障成功,否则机械臂运动到Jmin,跳转到第1)步.
局部极小处理流程如下:
1) 计算机械臂进入局部极小总次数w,若w>wmax,则避障失败.
2) 求解虚拟目标角度
3) 若当前朝γi运动,将算法主流程中的所有目标角度γi替换为
4) 若机械臂到达虚拟目标角度或当前朝
利用本文建立的Jaco2七自由度机械臂模型对算法进行仿真验证.算法参数设定:Ka=20 000,Sc=100,λ0=3 °,λ1=1 °,
|
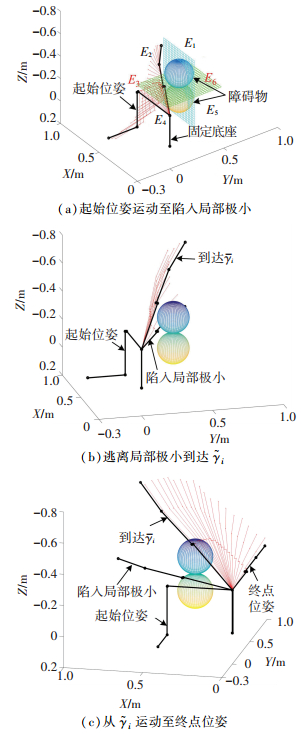
图 4 机械臂运动轨迹 Fig. 4 Trajectory of the manipulator |
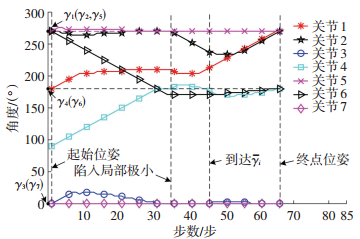
本组仿真实验中,起始运动关节角度、陷入局部极小时关节角度、虚拟目标角度
| 表 2 不同状态下各关节角度 Tab. 2 Angle of each joint in different states |
仿真过程中各关节角度变化如图 5所示,机械臂运动轨迹依次如图 4(a)、4(b)、4(c)所示. 图 5中,机械臂运动步数为1、35、46、66时的位姿分别与图 4中的起始位姿、陷入局部极小位姿、到达
|
图 5 机械臂各关节角度变化 Fig. 5 Change of angle of each joint |
文献[17]中,建立机械臂引导势场时采用的算法为传统人工势场法,本文利用加拿大Kinova公司的Jaco2七自由度冗余机械臂,对提出的改进人工势场法与以文献[17]建立势场时采用的算法为例进行对比实验.改进人工势场法的实验参数设定:Ka=20 000,Sc=100,λ0=3 °,λ1=1 °,
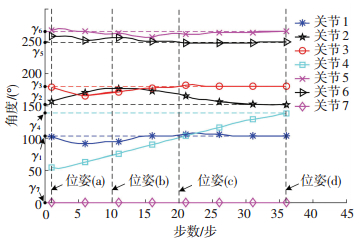
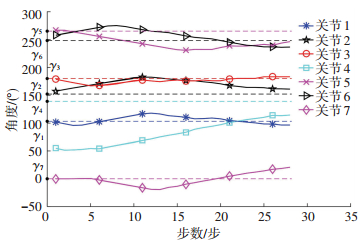
采用本文算法的机械臂避障过程如图 6所示.实验中,各关节起始运动角度、目标角度γi、采用改进算法运动终点角度及其与γi的误差、采用传统算法运动终点角度及其与γi的误差如表 3所示.实验中两种算法采用相同的起始位姿与目标位姿.由表 3可知,针对串联型冗余机械臂,采用改进算法时运动终点角度与γi的误差较小,其中6号关节角度误差最大,仅为0.8 °,在机械臂运动误差范围之内,表明本文提出的改进算法在引导末端到达目标位姿的同时,可以保证各关节角度到达γi;而采用传统算法时,各关节运动终点角度与γi之间误差普遍较大,最大高达24.6 °,表明采用传统算法虽然能够引导机械臂末端到达目标位姿,但不能对各个关节运动进行有效约束.

|
图 6 改进人工势场法避障过程 Fig. 6 Obstacle avoidance process by improved artificial potential field method |
| 表 3 不同状态下各关节角度 Tab. 3 Angle of each joint in different states |
终点位姿下,末端的位姿误差包括位置误差与姿态误差.定义末端的位置误差为
| $ {e_{\rm{s}}} = \left\| {\mathit{\boldsymbol{P}}_{\rm{e}}^0 - \mathit{\boldsymbol{P}}_{\rm{g}}^0} \right\|_2^2. $ |
式中Pe0为终点位姿下,末端坐标系原点在基坐标系x0-z0下的坐标向量.定义末端姿态误差为
| $ {e_{\rm{ \mathsf{ φ} }}} = \left\| {{\mathit{\boldsymbol{\varphi }}_{\rm{e}}} - {\mathit{\boldsymbol{\varphi }}_{\rm{g}}}} \right\|_2^2. $ |
式中
| 表 4 基坐标系下末端位姿 Tab. 4 Pose of the end in basic coordinate system |
由表 4可知:本组实验中,采用改进算法避障完成时位置误差与姿态误差分别为0.012 m和1.99 °,均低于传统算法;对12组实验结果求取平均误差,采用改进算法时的平均位置误差和平均姿态误差分别为0.010 m和2.40 °,低于传统算法的0.019 m和11.71 °.对比表明,相较于传统算法,采用改进算法避障完成时末端位姿与目标位姿更为接近,末端位姿定位精度更高.针对串联型冗余机械臂,改进算法在避障结束时关节角度误差、末端位姿误差均小于传统算法,原因是改进算法可在关节空间中建立引力势场,引导与约束各独立关节运动,当各关节到达目标角度后,机械臂整体位姿与目标位姿相近,可进一步提高末端定位精度,而传统算法仅在末端建立势场,当末端位姿确定时有无数组关节角度与之对应,无法引导与约束各关节运动,则整体位姿可能与目标位姿产生较大差别,同时受障碍物斥力势场影响,末端位姿误差较大.
采用两种算法进行对比实验时,各关节角度随运动过程的变化分别如图 7、图 8所示. 图 7中机械臂运动步数为1、10、20、36时的位姿分别如图 6(a)、图 6(b)、图 6(c)、图 6(d)所示.在30组对比实验中,采用改进算法均避障成功,证明了算法有效性.对比图 7、图 8可知,当采用两种算法时,各关节角度值在运动过程中由于避障出现了波动,当采用改进算法时,关节1、关节2、关节5、关节6、关节7波动幅度均比传统算法小,采用两种算法时关节3的波动幅度基本相同,关节4整体呈现出趋向于γ4的趋势.对比表明,在避障过程中,改进算法相较于传统算法各关节角度值整体波动幅度较小,则关节运动幅度较小,原因是改进算法可在关节空间中建立引力势场,在避障过程中对各关节运动进行引导与约束,完成避障的前提下引力势场值向减小方向变化,即引导关节向目标角度方向运动,而传统算法仅针对末端建立势场,无法对关节进行有效引导与约束,仅可通过碰撞检测算法保证其不与障碍物发生碰撞,而不能保证关节向目标角度运动.
|
图 7 改进人工势场法各关节角度变化 Fig. 7 Change of angle of each joint by improved APFM |
|
图 8 传统人工势场法各关节角度变化 Fig. 8 Change of angle of each joint by traditional APFM |
1) 提出在笛卡尔空间内建立目标点引力势场和障碍物斥力势场、在关节空间中建立目标角度引力势场相结合的算法,算法可有效引导机械臂从起始位姿避开障碍物到达目标位姿.
2) 提出在关节空间内求解虚拟目标角度,并采用高斯函数建立虚拟引力势场处理局部极小问题.仿真结果表明,算法可顺利引导机械臂逃离局部极小,最终完成避障到达目标位姿.
3) 改进算法提高了避障结束时末端位姿的定位精度,减小了避障过程中关节运动幅度.实验结果表明:改进算法避障完成时各关节角度误差、末端平均位置与姿态误差分别为0.8°、0.010 m和2.40°,均优于传统算法;避障过程中关节角度整体波动幅度小于传统算法.
4) 本文算法对冗余机械臂避障研究及应用具有一定的指导意义,受凹型障碍物影响的局部极小问题与虚拟引力势场建立算法是后续研究的重点.
| [1] |
GONCALVES V M, FRAISSE P, CROSNIER A, et al. Parsimonious kinematic control of highly redundant robots[J]. IEEE Robotics & Automation Letters, 2017, 1(1): 65. DOI:10.1109/LRA.2015.2506259 |
| [2] |
YOO Y J, OH K J, CHOI Y J, et al.Obstacle avoidance for redundant manipulator without information of the joint angles[C]//Control Conference.Piscattaway, NJ: IEEE, 2013: 1
|
| [3] |
KO N Y. Extended RMRC and its application to the motion of a mobile manipulator[J]. International Journal of Humanoid Robotics, 2015, 12(2): 1550016. DOI:10.1142/S0219843615500164 |
| [4] |
CHEN Yujin, JU Mingyi, HWANG Kaoshing. A virtual torque-based approach to kinematic control of redundant manipulators[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1728. DOI:10.1109/TIE.2016.2548439 |
| [5] |
KARPINSKA J, TCHON K. Performance-oriented design of inverse kinematics algorithms: extended jacobian approximation of the jacobian pseudo inverse[J]. Journal of Mechanisms & Robotics, 2012, 4(2): 437. DOI:10.1115/1.4006192 |
| [6] |
HUANG Shuihua, PENG Yonggang, WEI Wei, et al. Clamping weighted least-norm method for the manipulator kinematic control with constraints[J]. International Journal of Control, 2016, 89(11): 2240. DOI:10.1080/00207179.2016.1153151 |
| [7] |
DONG Hui, DU Zhijiang. Obstacle avoidance path planning of planar redundant manipulators using workspace density[J]. International Journal of Advanced Robotic Systems, 2015, 12(9): 1. DOI:10.5772/59973 |
| [8] |
ABU-DAKKA F J, VALERO F J, SUNER J L, et al. A direct approach to solving trajectory planning problems using genetic algorithms with dynamics considerations in complex environments[J]. Robotica, 2015, 33(3): 669. DOI:10.1017/S0263574714000393 |
| [9] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100. DOI:10.1109/TSSC.1968.300136 |
| [10] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International Journal of Robotics Research, 1986, 5(1): 90. DOI:10.1109/ROBOT.1985.1087247 |
| [11] |
于振中, 闫继宏, 赵杰, 等. 改进人工势场法的移动机器人路径规划[J]. 哈尔滨工业大学学报, 2011, 43(1): 50. YU Zhenzhong, YAN Jihong, ZHAO Jie, et al. Mobile robot path planning based on improved artificial field method[J]. Journal of Harbin Institute of Technology, 2011, 43(1): 50. DOI:10.11918/j.issn.0367-6234.2011.01.011issn.0367-6234.2011.01.011 |
| [12] |
HARGAS Y, MOKRANE A, HENTOUT A, et al.Mobile manipulator path planning based on artificial potential field: Application on RobuTER/ULM[C]//International Conference on Electrical Engineering. Piscattaway, NJ: IEEE, 2016: 1
|
| [13] |
OH J, BAR H, OH J H.Analytic inverse kinematics considering the joint constraints and self-collision for redundant 7DOF manipu-lator[C]//IEEE International Conference on Robotic Computing.Piscattaway, NJ: IEEE, 2017: 123
|
| [14] |
MOTAHARI A, ZOHOOR H, KORAYEM M H. A new obstacle avoidance method for discretely actuated hyper-redundant manipula-tors[J]. Scientia Iranica, 2012, 19(4): 1081. DOI:10.1016/j.sci-ent.2012.06.017 |
| [15] |
王俊龙, 张国良, 羊帆, 等. 改进人工势场法的机械臂避障路径规划[J]. 计算机工程与应用, 2013, 49(21): 266. WANG Junlong, ZHANG Guoliang, YANG Fan, et al. Improved artificial field method on obstacle avoidance path planning for manipulator[J]. Computer Engineering and Applications, 2013, 49(21): 266. DOI:10.3778/j.issn.1002-8331.1201-0360 |
| [16] |
LIU S, ZHANG Q, ZHOU D. Obstacle avoidance path planning of space manipulator based on improved artificial potential field method[J]. Journal of the Institution of Engineers, 2014, 95(1): 31. DOI:10.1007/s40032-014-0099-z |
| [17] |
CHENG Fengyi, JI Wei, ZHAO Dean, et al.Apple picking robot obstacle avoidance based on the improved artificial potential field method[C]//IEEE Fifth International Conference on Advanced Computa-tional Intelligence. Piscattaway, NJ: IEEE, 2012: 909.DOI: 10.1109/ICACI.2012.6463303
|
 2019, Vol. 51
2019, Vol. 51


