2. 重庆青山工业技术中心,重庆 402761
2. Chongqing Qingshan Industrial Technology Center, Chongqing 402761, China
同步器是MT/AMT/DCT/EMT变速器中核心换挡零部件,对汽车换挡性能和操纵舒适性有重要影响[1-5].陈震等[6]利用ADAMS建立了同步器多刚体运动学模型,分析了换挡力等参数对同步过程的影响.余晓霞等[7]运用AMESim建立了同步器换挡性能动力学仿真模型, 分析了同步环摩擦系数、摩擦锥角等因素对换挡性能的影响.戴丰等[8]基于磨合磨损分形理论,建立了换挡同步器接触磨损数学模型.徐万里等[9]利用扫描电镜对同步器摩擦表面进行观察,发现随着换挡次数增加,摩擦表面微凸体被磨损,摩擦系数降低,粗糙接触转矩下降. Häggström D等[10]建立了同步器结合过程摩擦系数变化规律预测模型,并对同步器锁环和摩擦锥环温度变化进行了仿真. Abraham M等[11]研究了润滑油对同步器结合过程中摩擦系数的影响.综上所述,目前国内外学者对同步器结合过程有一定研究,但多以商业软件为基础,主要分析了同步器结构参数对同步时间、同步力矩等性能参数的影响.研究主要偏向于实际工程问题且处于宏观结构影响因素分析阶段,对同步器结合过程缺乏深度理论研究,对同步环宽度、同步环半径、摩擦锥角以及摩擦材料厚度等因素对同步过程的影响规律没有进行研究.
针对国内外研究的不足,本文建立了同步器结合过程中油膜压力、微凸体接触力、同步环轴向力、同步力矩等数学模型,采用4-Runge-Kutta法对油膜厚度和同步转速差进行求解,分析了同步环宽度、同步环半径、摩擦锥角以及摩擦材料厚度对同步器结合过程的影响.
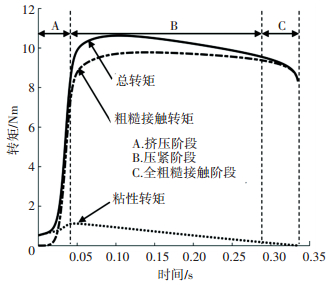
1 同步器摩擦模型 1.1 同步器简介锁环式同步器主要由花键毂、结合套、带结合齿圈、同步环、摩擦锥环、滑块、压簧等零件组成.变速器换挡过程中同步器主要经历了第一次自由滑移、预同步、同步、同步环拨转、第二次自由滑移、二次冲击、齿轮拨转、齿轮啮合共8个过程[12-13].同步器同步过程发生在预同步和同步阶段,其主要经历了挤压阶段、压紧阶段、全粗糙接触3个阶段,如图 1所示.
|
图 1 同步器摩擦阶段划分 Fig. 1 Division of synchronizer friction phase |
在挤压阶段,同步力矩主要由油液粘性转矩承担;在压紧阶段,同步力矩由油液粘性转矩和粗糙接触转矩共同承担;在全粗糙接触阶段,同步力矩主要由粗糙接触转矩承担.同步过程中,油膜厚度不断减小,转速差不断降低.油膜厚度和转速差变化主要与油膜压力、微凸体承载力、粘性剪切力矩、粗糙接触转矩等因素有关.
1.2 油膜压力模型同步过程中同步环与摩擦锥环相对转动,作用在结合套上的轴向力使得同步环与摩擦锥环之间的间隙不断减小,间隙内的润滑油不断被挤出或渗透到摩擦锥环表面.由于同步环摩擦锥角略大于摩擦锥环摩擦锥角,所以当同步环向摩擦锥环做轴向运动时,同步环和摩擦锥环狭小空间中润滑油运动规律满足雷诺方程[14].针对同步环和摩擦锥环之间油液的挤压运动,做出以下假设:
1) 油膜在摩擦副表面上无相对滑动.
2) 与剪切力相比,油膜所受体积力可忽略不计.
3) 由于同步环和摩擦锥环之间轴向间隙小,故假设油膜压力沿油膜厚度无变化.
4) 油膜径向压力梯度为零.
5) 润滑油为牛顿流体,遵循牛顿粘性定理.
6) 由于同步时间较短,且变速器润滑油粘温曲线较为稳定,故假定同步过程中润滑油粘度不变.
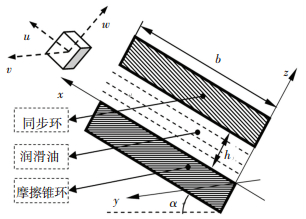
针对以上假设,建立同步器结合过程中油液挤压模型三维坐标系,如图 2所示.
|
图 2 油膜挤压模型坐标系 Fig. 2 Oil film extrusion model coordinate system |
由于同步过程中润滑油密度不随时间变化,同步环与摩擦锥环之间的油液成轴向对称分布,且油液剪切过程中同步环表面油液单元体分别在x、y两个方向的变化梯度为零,所以同步环和摩擦锥环间的润滑油满足以下雷诺方程:
| $ \frac{\partial }{{\partial x}}\left( {\frac{{{h^3}\partial p}}{{\partial x}}} \right) = 6\eta \left( {{u_2} - {u_1}} \right)\frac{{\partial h}}{{\partial x}} + 12\eta \left( {{w_1} - {w_2}} \right). $ | (1) |
式中:p为油膜压力,η为动力粘度,h为两表面的平均间隙,u1、w1分别为摩擦锥环表面油液单元体在x、y两个方向速度,u2、w2分别为同步环表面油液单元体在x、y两个方向速度.
已知圆周方向油膜厚度为一常数
| $ \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{h^{3} \mathrm{d} p}{\mathrm{d} x}\right)=12 \eta \frac{\mathrm{d} h}{\mathrm{d} t}, $ | (2) |
式中,t为同步时间.考虑压力流量因素和同步环摩擦材料渗透性,假设同步环摩擦材料厚度为d.根据同步环和摩擦锥环间实际运动情况,则式(2)可化为
| $ \frac{{\rm{d}}}{{{\rm{d}}x}}\left( {{\mathit{\Phi }_x}\left( {{h^3} + 12\mathit{\Phi }d} \right)\frac{{{\rm{d}}p}}{{{\rm{d}}x}}} \right) = 12\eta \frac{{{\rm{d}}h}}{{{\rm{d}}t}}, $ | (3) |
式中,Φ为同步环摩擦材料渗透性,Φx为x轴方向patir和cheng压力流量因素,其大小为[15-16]
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\Phi }_x} = 1 - C{{\rm{e}}^{ - rH}},}&{\gamma \le 1;}\\ {{\mathit{\Phi }_x} = 1 + C{{\rm{e}}^{ - rH}},}&{\gamma > 1.} \end{array}} \right. $ | (4) |
式中:γ为方向性参数; C, r为与γ相关常数,其中0.87≤C≤1.48,0.42≤r≤1.5,0.11≤γ≤9; H为膜厚比,其大小为H=h/σ, σ为联合粗糙度,其大小为
| $ \sigma = \sqrt {\sigma _1^2 + \sigma _2^2} , $ | (5) |
式中,σ1、σ2分别为同步环和摩擦锥环表面粗糙度.
同步过程中油膜压力可由式(3)两边同时对x求积分得到
| $ p = \frac{{6\eta {x^2}}}{K}\frac{{{\rm{d}}h}}{{{\rm{d}}t}} + \frac{{{C_1}}}{K}x + {C_2}. $ | (6) |
式中:K=Φx(h3+12Φd),d为同步环摩擦材料厚度,C1, C2分积分常数.
同步环和摩擦锥环之间油膜压力边界条件为
| $ \left\{ \begin{array}{l} p\left( {x = 0} \right) = 0,\\ p\left( {x = b} \right) = 0. \end{array} \right. $ | (7) |
将式(7)代入式(6)求出积分常数C1、C2,再将其代入式(6)求得油膜压力分布为
| $ p = \frac{{6\eta }}{K}\left( {bx - {x^2}} \right)\frac{{{\rm{d}}h}}{{{\rm{d}}t}}. $ | (8) |
假设同步环和摩擦锥环两表面粗糙峰高度都服从均值为零的高斯概率分布,则两表面平均间隙h为
| $ h = \frac{{{h_{{\rm{oil}}}}}}{2}\left[ {1 + {\rm{erf}}\left( {\frac{{{h_{{\rm{oil}}}}}}{{\sqrt 2 \sigma }}} \right)} \right] + \frac{\sigma }{{\sqrt {2\pi } }}\exp \left( { - \frac{{h_{{\rm{oil}}}^2}}{{2{\sigma ^2}}}} \right). $ | (9) |
式中,hoil为两摩擦表面间油膜厚度,erf()表示误差函数,其计算方法为
| $ \operatorname{erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} \mathrm{e}^{-\eta^{2}} \mathrm{d} \eta $ | (10) |
根据链式求导法则可得
| $ \frac{\mathrm{d} h}{\mathrm{d} t}=\left\{\frac{1}{2}\left[1+\operatorname{erf}\left(\frac{h_{\mathrm{oil}}}{\sqrt{2} \sigma}\right)\right]\right\} \frac{\mathrm{d} h_{\mathrm{oil}}}{\mathrm{d} t}. $ | (11) |
令
| $ p_{\text { oil }}=\frac{6 \eta}{K}\left(b x-x^{2}\right) g\left(h_{\text { oil }}\right) \frac{\mathrm{d} h_{\text { oil }}}{\mathrm{d} t} $ | (12) |
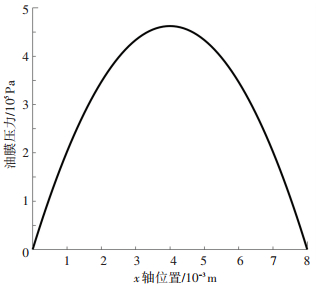
由式(12)可知,油膜压力大小与径向位置、润滑油粘度、摩擦材料渗透性、同步环宽度以及油膜厚度变化率有关.采用数值分析方法,将相关参数代入式(12)中,得到初始油膜压力如图 3所示.
|
图 3 初始油膜压力分布 Fig. 3 Initial pressure distribution of oil film |
由图 3可知,同步开始时刻同步环和摩擦锥环间两边压力最小,中间压力最大.在初始时刻油液受到挤压向同步环和摩擦锥环两边间隙运动,从而产生了中间压力大,间隙两边压力小的现象.
1.3 微凸体接触力模型随着油膜厚度不断减小,微凸体接触力不断增大.假设同步环与摩擦锥环之间只发生弹性摩擦,则微凸体接触压力计算模型可表示为[17]
| $ {p_c}\left( H \right) = \frac{{16\sqrt 2 }}{{15}}{\rm{ \mathsf{ π} }}{\left( {\lambda \beta \sigma } \right)^2}E'\sqrt {\frac{\sigma }{\beta }} A{F_{\frac{s}{2}}}\left( H \right). $ | (13) |
式中:H为膜厚比,λ为摩擦表面粗糙峰密度,β微凸峰曲率半径,σ为联合粗糙度,E′为两摩擦表面当量弹性模量,A为同步环和摩擦锥环摩擦表面名义接触面积,Fn(H)为膜厚比相关函数.其中E′、Fn(H)计算方法为
| $ \frac{1}{{E'}} = \frac{1}{2}\left[ {\frac{{1 - \upsilon _1^2}}{{{E_1}}} + \frac{{1 - \upsilon _2^2}}{{{E_2}}}} \right] $ | (14) |
| $ {F_n}\left( u \right) = \int_u^\infty {{{\left( {s - u} \right)}^n}{\varphi ^ * }\left( s \right){\rm{d}}s} $ | (15) |
式中:E1、E2分别为摩擦锥环和同步环弹性模量,υ1, υ2分别为摩擦锥环和同步环泊松比,
| $ {\varphi ^ * }\left( s \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - \frac{1}{2}{s^2}}}. $ | (16) |
根据Greenwood J A和Williamson J B P研究表明,大多粗糙表面取值范围为λβσ=0.03~0.05[18].本文中同步环为特种黄铜合金,摩擦锥环为高碳合金钢,λβσ=0.05、σ/β=0.011 3、E′=2.7×108 Pa.
将式(14)、式(15)和式(16)代入式(13)计算出微凸体表面接触压力为
| $ \left\{ \begin{array}{l} {p_c}\left( H \right) = {\left( {\lambda \beta \sigma } \right)^2}E' \times 1.1104 \times {10^{ - 5}}{\left( {4.0 - H} \right)^{6.084}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H < 4.0;\\ {p_c}\left( H \right) = 0,\;\;\;\;\;H \ge 4.0. \end{array} \right. $ | (17) |
由式(17)可知,当同步环和摩擦锥环接触表面膜厚比H≥4.0时,微凸体压力大小为零;当膜厚比H < 4.0时,微凸体接触压力与摩擦表面粗糙峰密度λ、微凸峰曲率半径β、联合粗糙度σ、两摩擦表面当量弹性模量E′以及膜厚比H相关.
1.4 同步环轴向力模型同步器结合过程中由于受结合套轴向分力作用,同步环不断向摩擦锥环做轴向运动.同步环所受轴向力由油膜压力和微凸体承载力共同组成.同步环所受轴向力为
| $ {F_{{\rm{total}}}} = \left( {1 - B} \right){F_{{\rm{oil}}}} + B{F_c} $ | (18) |
式中:Foil为油膜承载力;Fc为微凸体承载力;B为微凸体接触面积与总面积之比,计算方法为
| $ \begin{array}{l} B = \frac{{{{\rm{ \mathsf{ π} }}^2}{{\left( {\lambda \beta \sigma } \right)}^2}}}{2}\left\{ {\left( {1 + {H^2}} \right)\left[ {1 - {\rm{erf}}\left( {\frac{H}{{\sqrt 2 }}} \right)} \right] - } \right.\\ \;\;\;\;\;\;\left. {\frac{{\sqrt 2 }}{{\sqrt {\rm{ \mathsf{ π} }} }}H\exp \left( {\frac{{{H^2}}}{2}} \right)} \right\} \end{array} $ | (19) |
其中0≤B≤1,当B=0时表示同步环轴向力全部由油膜承担,当B=1时表示同步环轴向力全部由微凸体承担.根据图 2所建坐标系,对式(12)和式(17)在摩擦表面积分,求得Foil、Fc分别为
| $ {F_{{\rm{oil}}}} = {\rm{ \mathsf{ π} }}{b^3}\eta \left( {2r + b\sin \alpha } \right)\frac{{g\left( {{h_{{\rm{oil}}}}} \right)}}{K}\frac{{{\rm{d}}{h_{{\rm{oil}}}}}}{{{\rm{d}}t}}. $ | (20) |
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {F_c} = \left( {2r + b\sin \alpha } \right){\rm{ \mathsf{ π} }}b{p_c},\\ {F_c} = 0, \end{array}&\begin{array}{l} H < 4.0;\\ H \ge 4.0. \end{array} \end{array}} \right. $ | (21) |
假设同步过程中,同步环向摩擦锥环的运动是一个准静态过程,则同步环所受轴向力Ftotal等于结合套所受轴向力Fsleevesin α,即Ftotal=Fsleevesin α.结合式(12)、式(17)、式(20)、式(21)可解得油膜变化率为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{h_{{\rm{oil}}}}}}{{{\rm{d}}t}} = \frac{{\left[ {{F_{{\rm{sleeve}}}}\sin \alpha - B{\rm{ \mathsf{ π} }}b{p_c}\left( {2r + b\sin \alpha } \right)} \right]K}}{{\left( {1 - B} \right)\eta {\rm{ \mathsf{ π} }}{b^3}g\left( {{h_{{\rm{oil}}}}} \right)\left( {2r + b\sin \alpha } \right)}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H < 4.0;\\ \frac{{{\rm{d}}{h_{{\rm{oil}}}}}}{{{\rm{d}}t}} = \frac{{{F_{{\rm{sleeve}}}}\sin \alpha K}}{{\left( {1 - B} \right)\eta {\rm{ \mathsf{ π} }}{b^3}g\left( {{h_{{\rm{oil}}}}} \right)\left( {2r + b\sin \alpha } \right)}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H \ge 4.0. \end{array} \right. $ | (22) |
由式(22)可知,油膜变化率与同步环摩擦材料厚度d、摩擦材料渗透性Φ、油膜厚度h等因素成正相关,与润滑油粘度η、同步环宽度b、同步环半径r、摩擦锥角α等因素成负相关.
1.5 同步力矩计算模型同步器结合过程中同步环和摩擦锥环之间主要经过了挤压、压紧以及全粗糙接触3个阶段.同步力矩主要由剪切油膜的粘性转矩Toil和微凸体接触的摩擦转矩Tc共同组成,其同步力矩大小为
| $ T = \left( {1 - B} \right){T_{{\rm{oil}}}} + B{T_c}. $ | (23) |
式中,剪切油膜的粘性转矩Toil和微凸体接触的摩擦转矩Tc分别为
| $ {T_{{\rm{oil}}}} = \left( {{\varphi _f} + {\varphi _{fs}}} \right)\frac{{\pi \eta \omega }}{{2h}}\left[ {{{\left( {r + b\sin \alpha } \right)}^4} - {r^4}} \right]. $ | (24) |
| $ \left\{ \begin{array}{l} {T_c} = \left( {2{r^2} + 2rb\sin \alpha + 0.5{b^2}{{\sin }^2}\alpha } \right){\rm{ \mathsf{ π} }}b{f_c}{p_c},H < 4.0;\\ {T_c} = 0,\;\;\;\;\;H \ge 4.0. \end{array} \right. $ | (25) |
式中:
利用同步器单体试验台,对摩擦锥环与同步环所组成的摩擦副进行滑磨试验,得到摩擦系数随滑磨速度的变化规律.通过对试验数据曲线拟合,得到了摩擦系数随滑磨速度的数学模型:
| $ {f_c} = 0.12 + 0.002\log \left( \omega \right). $ | (26) |
式中,ω为同步环和摩擦锥环相对滑磨速度.
同步过程中,同步环与整车相连、摩擦锥环与离合器从动盘相连.整车转动惯量大、离合器从动盘惯量小,摩擦锥环会被加速或减速(降挡时为加速,升挡时为减速).根据同步器输入端转速变化规律,同步力矩等于
| $ T = I\frac{{{\rm{d}}{\omega _i}}}{{{\rm{d}}t}}. $ | (27) |
式中:I为同步器输入端等效转动惯量,ωi为摩擦锥环转速.将式(23)、式(24)以及式(25)代入式(27)整理可得
| $ \begin{array}{l} \frac{{{\rm{d}}{\omega _i}}}{{{\rm{d}}t}} = \frac{{{\rm{ \mathsf{ π} }}\eta \omega }}{{2hI}}\left( {{\varphi _f} + {\varphi _{fs}}} \right)\left( {1 - B} \right)\left[ {{{\left( {r + b\sin \alpha } \right)}^4} - {r^4}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{B}{I}\left( {2{r^2} + 2rb\sin \alpha + 0.5{b^2}{{\sin }^2}\alpha } \right){\rm{ \mathsf{ π} }}b{f_c}{p_c}. \end{array} $ | (28) |
由式(28)可知,同步转速变化速率与润滑油粘度η、微凸体接触面积与总面积之比B、同步器输入端转动惯量I、同步环半径r、同步环宽度b、摩擦锥角α、摩擦系数fc、油膜压力pc等因素相关.
2 数值仿真与试验验证 2.1 数值求解初始值基于某款国产变速器实测数据,利用所建模型对同步器结合过程进行仿真.仿真参数如表 1所示.
| 表 1 仿真相关参数 Tab. 1 Simulation related parameters |
将初始数值输入到所建模型,采用4-Runge-Kutta法对式(22)和式(28)进行耦合求解,同步计算出油膜厚度和转速差.其中迭代步长为0.001,初始转速差为684 r/min.当转速差小于0.001 r/min时默认为同步完成.
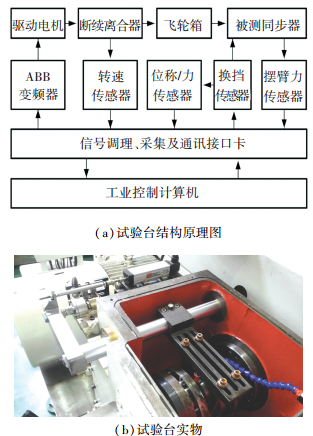
2.3 模型验证 2.3.1 台架原理为验证所建同步器结合过程数学模型的准确性,依托现有同步器单体试验台(如图 4所示)对同步器结合过程进行了试验验证.
|
图 4 同步器单体试验台 Fig. 4 Single synchronizer test rig |
同步器单体试验时,工控机通过变频器控制驱动电机工作,驱动飞轮转动;当同步器输出端达到规定转速后,断续离合器工作,模拟整车动力中断工况下换挡过程,同时换挡机器人控制换挡拨叉实现同步器结合.安装于换挡机器人上的换挡力传感器和换挡位移传感器分别测得同步器结合过程中换挡力和换挡位移,而同步力矩则利用同步器输入端摆臂力传感器的测量结果换算得到.
2.3.2 试验与仿真对比为确保仿真与试验一致性,参照仿真条件以及同步器实际工作环境设置试验工况,具体试验工况相关参数如表 2所示.
| 表 2 试验相关参数 Tab. 2 Test related parameters |
分别提取转速差和同步力矩试验数据与仿真结果进行对比,其对比结果如图 5所示.
|
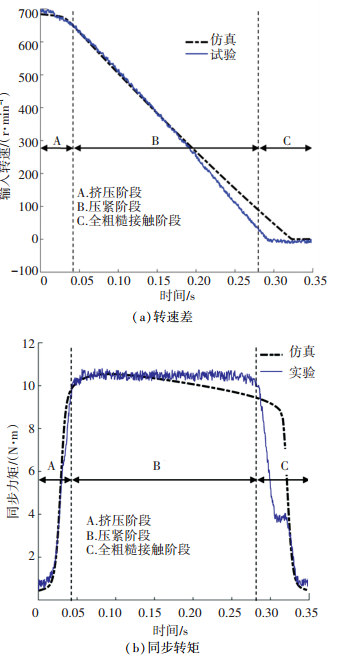
图 5 试验与仿真结果对比 Fig. 5 Comparison results of experiment and simulation |
由图 5可知,同步器结合过程中转速差、同步力矩及同步时间的仿真与试验结果总体吻合度较好,其大总转矩相差0.08 N·m,同步时间相差0.011 s.由图 5(a)可以看出,在挤压阶段转速差的仿真与试验结果一致性较好,但随着转速差减小,仿真与试验结果开始出现差异,这主要是由于仿真分析时未计入系统摩擦阻力且摩擦系数随转速差变化规律不够准确所引起.从图 5(b)可知,挤压阶段同步力矩的仿真与试验结果吻合度较高,但在压紧和全粗糙接触阶段试验测得的同步力矩略微偏大,这也是由于仿真分析时引入的摩擦系数随转速差变化规律欠准确所导致.
通过仿真与试验结果对比分析可知,本文建立的同步器结合过程数学模型能够较为准确地表征其同步过程的同步机理.因此,基于本文所建数学模型,运用仿真分析方法深入研究了同步器结构参数对其同步性能的影响规律.
3 同步器结构参数对同步过程的影响同步器结构参数是同步器性能的关键影响因素之一,不同结构参数对同步性能具有不同的影响规律.由于同步器结构参数较多,本文主要依据某同步器生产企业对其典型结构参数设计开发要求,分别分析了同步环宽度、同步环半径、摩擦锥角以及摩擦材料厚度对同步器结合过程的影响规律,具体结构参数如表 3所示.
| 表 3 结构仿真参数 Tab. 3 Structure simulation parameters |
为定量化分析同步器典型结构参数对同步过程的影响规律,对粗糙接触转矩峰值、粘性转矩峰值、粗糙接触转矩响应时间、同步时间进行了定义,如图 6所示.
|
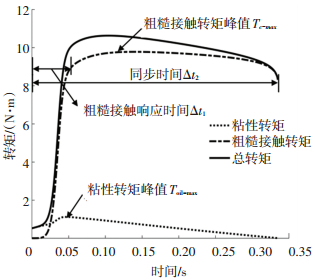
图 6 同步过程相关参数定义 Fig. 6 Definition of synchronization parameters |
如图 6所示,粗糙接触转矩峰值Tc-max为同步器同步过程中最大粗糙接触转矩,粘性转矩峰值Toil-max为同步过程中最大粘性转矩,粗糙接触转矩响应时间Δt1为同步开始至粗糙接触转矩到达粗糙接触转矩峰值90%所需时间,同步时间Δt2为同步开始至转速差为零所需时间.
3.1 同步环宽度为了分析同步环宽度对同步器结合过程影响规律,分别对2种同步环宽度的同步器结合过程进行了仿真分析,如图 7所示.
|
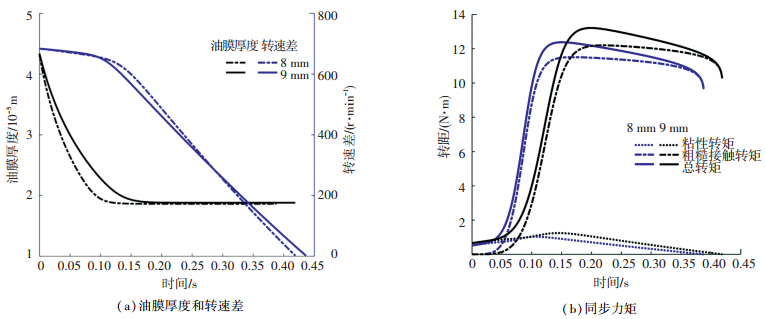
图 7 同步环宽度对同步过程的影响 Fig. 7 Effect of synchronizer ring width to synchronization |
由图 7(a)、(b)可知,同步环宽度对同步器结合过程影响较大.同步环宽度增大1 mm,油膜厚度减小速率变缓,最小油膜厚度无明显变化,粘性转矩峰值增大0.19 N·m,粗糙接触转矩峰值增大0.92 N·m,粗糙接触转矩响应滞后0.044 s,同步时间增加0.032 s.这是由于同步环宽度增加,导致同步环和摩擦锥环之间摩擦面积增加,从而使得摩擦副间润滑油挤排阻力增加且粗糙接触转矩增大,油膜承载与剪切过程更长,粗糙接触被滞后,同步时间增大.适当减小同步环宽度可以缩短同步环时间,提高同步性能,但过小的同步环宽度会降低同步器耐久可靠性.
3.2 同步环半径同步环半径不仅会影响同步器结构大小,对同步器结合过程也有重要影响.为探明同步环半径对同步过程的影响规律,对2种同步环半径下同步器结合过程进行了仿真,结果如图 8所示.
|
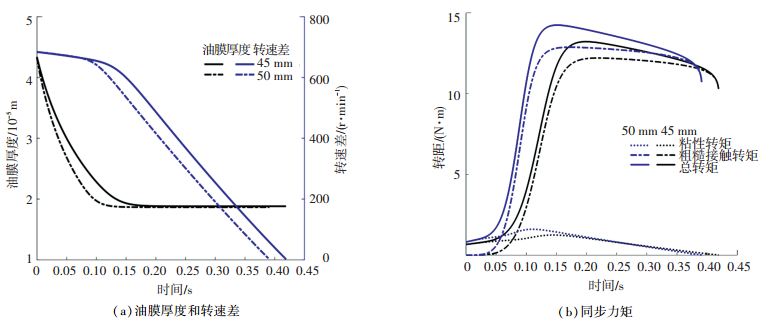
图 8 同步环半径对同步过程的影响 Fig. 8 Effect of synchronizer ring radius to synchronization |
由图 8(a)、(b)可知,同步环半径对同步器结合过程有着重要.同步环半径增大5 mm,初始挤压阶段油膜厚度变化速率加快,粘性转矩峰值增大0.29 N·m,粗糙接触转矩峰值增大1.65 N·m,粗糙接触转矩响应提前0.048 s,同步时间缩短0.031 s.由于同步环半径增加,导致同步环和摩擦锥环之间摩擦面积增加,所以粘性转矩峰值、粗糙接触转矩峰值增大.当同步环半径增大时,在相同转速下润滑油所受离心力增大,从而润滑油被快速排出到间隙外;润滑油迅速的减少,导致粗糙接触转矩相应加快,同步时间缩短.由式(25)可知,同步环半径增大,粗糙接触转矩增大.在满足结构条件情况下,适当增大同步环和摩擦锥环半径,可以有效增大同步力矩,缩短同步时间, 提升同步性能.
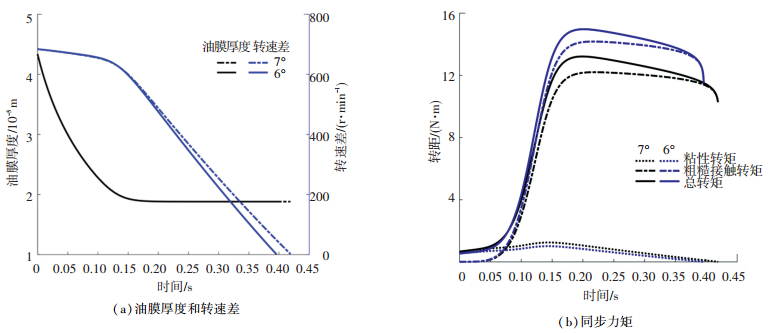
3.3 摩擦锥角同步环摩擦锥角是同步器重要的设计参数.同步环摩擦锥角大小对同步力矩和同步时间有重要影响.为探明摩擦锥角对同步器结合过程的影响,对不同大小摩擦锥角下同步器结合过程进行了仿真,其仿真结果如图 9所示.
|
图 9 摩擦锥角对同步过程的影响 Fig. 9 Effect of cone angle to synchronization |
由图 9(a)、(b)可知,摩擦锥角对同步器结合过程有着重要影响.摩擦锥角增大1°,油膜厚度变化规律无明显变化,压紧和全粗糙阶段转速差下降速率加快,粘性转矩峰值增大0.25 N·m,粗糙接触转矩峰值减小1.83 N·m,粗糙接触转矩响应滞后0.016 s,同步时间增加0.027 s.在结合套所受轴向力相同情况下,同步环摩擦锥角增大,摩擦副表面正压力减小,实际微凸体接触面积减小,从而粗糙接触转矩减小;同步环摩擦锥角增大,导致粘性转矩的等效半径增大(详见式(24)),所以粘性转矩增大,粗糙接触转矩响应延迟,同步时间延长.适当减小同步环摩擦锥角,有利于增大同步力矩,缩短同步时间.但摩擦锥角不易过大,过大容易造成同步器不能锁止;摩擦锥角也不易过小,过小容易使同步环卡死.
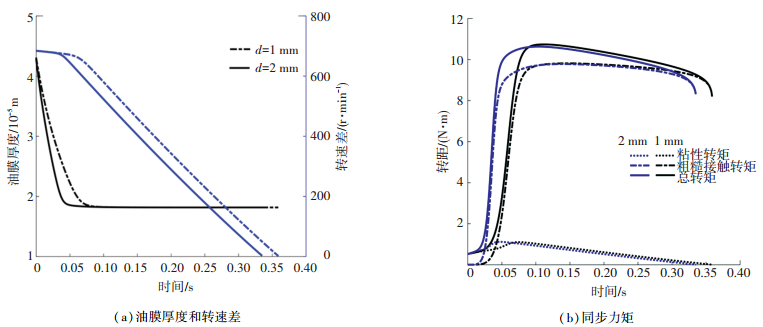
3.4 摩擦材料厚度不同摩擦材料厚度对同步器结合过程影响不同.为探明摩擦材料厚度对同步过程影响规律,对2种不同摩擦材料厚度下结合过程进行了仿真,其仿真结果如图 10所示.
|
图 10 摩擦材料厚度对同步过程的影响 Fig. 10 Effect of thickness of friction material to synchronization |
由图 10(a)、(b)可知,摩擦材料厚度主要影响了同步过程中的粗糙接触转矩响应时间和同步时间.同步环摩擦材料厚度增大1 mm,粘性转矩和粗糙接触转矩大小无明显变化,粗糙接触转矩响应提前0.031 s,同步时间减小0.032 s.摩擦材料厚度增大,粗糙接触转矩相应加快,粘性转矩和粗糙接触转矩大小基本没有变化.摩擦材料厚度减小,摩擦副表面储存润滑油能力下降,油膜厚度减小速度减缓,粗糙接触转矩响应延迟.适当增加摩擦材料厚度,可以加快粗糙接触转矩响应,缩短同步时间.但摩擦材料厚度过大,容易增加同步器设计制造成本.
4 结论1) 同步环宽度变化对最小油膜厚度影响较小,对同步力矩影响较大.同步环宽度减小,油膜厚度下降速率加快,粘性转矩和粗糙接触转矩减小,粗糙接触转矩响应迅速,同步时间缩短.
2) 最小油膜厚度和转速差下降速率与同步环半径大小无关. 2种同步环半径下同步过程中的粘性转矩和粗糙接触转矩大小和响应快慢不同.随着同步环半径增加,粘性转矩和粗糙接触转矩增大,油膜厚度下降速率加快,同步时间缩短.
3) 粘性转矩和粗糙接触转矩大小与同步环摩擦锥角相关性较大.同步环摩擦锥角增大,粘性转矩增大,粗糙接触转矩减小,转速差下降速率变缓,同步时间增加.
4) 摩擦副材料对粘性转矩和粗糙接触转矩大小影响较小,对油膜厚度下降速率和粗糙接触转矩响应快慢影响较大.摩擦副材料厚度减小,粗糙接触转矩相应延迟,油膜厚度下降速率减缓,同步时间延长.
| [1] |
TSENG C Y, YU C H. Advanced shifting control of synchronizer mechanisms for clutchless automatic manual transmission in an electric vehicle[J]. Mechanism & Machine Theory, 2015, 84: 37. |
| [2] |
LU T, LI H, ZHANG J, et al. Supervisor control strategy of synchronizer for wet DCT based on online estimation of clutch drag torque[J]. Mechanical Systems & Signal Processing, 2016, 66: 840. |
| [3] |
WALKER P D, ZHANG N. Engagement and control of synchroniser mechanisms in dual clutch transmissions[J]. Mechanical Systems & Signal Processing, 2012, 26(1): 322. |
| [4] |
LIN S, CHANG S, LI B. Gearshift control system development for direct-drive automated manual transmission based on a novel electromagnetic actuator[J]. Mechatronics, 2014, 24(8): 1214. DOI:10.1016/j.mechatronics.2014.09.008 |
| [5] |
PENTA A, GAIDHANI R, SATHIASEELAN S K, et al. Improvement in shift quality in a multi speed gearbox of an electric vehicle through synchronizer location optimization[C]// WCXTM 17: SAE World Congress Experience. 2017: 2
|
| [6] |
陈震, 钟再敏, 章桐. 基于ADAMS的同步器结合过程仿真分析[J]. 汽车工程, 2011, 33(4): 340. CHEN Zhen, ZHONG Zaimin, ZHANG Tong. Simulation analysis on the synchronizing process of synchronizer based on ADAMS[J]. Automotive Engineering, 2011, 33(4): 340. |
| [7] |
余晓霞, 张志刚, 苏洪. 基于AMESim同步器换挡性能仿真与优化[J]. 机械传动, 2018, 42(3): 60. YU Xiaoxia, ZHANG Zhigang, SU Hong. Simulation and optimization of synchronizer shift performance based on AMESim[J]. Mechanical Transmission, 2018, 42(3): 60. |
| [8] |
戴丰, 鲁统利, 张建武. 基于分形理论的同步器接触磨损模型[J]. 汽车技术, 2009(5): 15. DAI Feng, LU Tongli, ZHANG Jianwu. A model for synchronizer contact wear based on fractal theory[J]. Automotive Technology, 2009(5): 15. DOI:10.3969/j.issn.1000-3703.2009.05.004 |
| [9] |
徐万里, 赵巍, 张学明, 等. 变速箱同步器失效过程与失效机理分析[J]. 机械工程学报, 2014, 50(14): 69. XU Wanli, ZHAO Wei, ZHANG Xueming, et al. Analysis on failure process and failure mechanism of transmission synchronizer[J]. Mechanical Engineering Journal, 2014, 50(14): 69. |
| [10] |
HÄGGSTRÖM D, NYMAN P, SELLGREN U, et al. Predicting friction in synchronizer systems[J]. Tribology International, 2016, 97: 89. DOI:10.1016/j.triboint.2015.12.038 |
| [11] |
BROWN G, WALKER G M, FRIEND C, et al. Understanding MTF additive effects on synchroniser friction[J]. Sae International Journal of Fuels & Lubricants, 2012, 5(1): 447. |
| [12] |
吴荣华.同步器换档特性分析与优化设计[D].重庆: 重庆大学, 2012: 5 WU Ronghua.Analysis and optimal design for synchromesh behaviour[D]. Chongqing: Chongqing University, 2012: 5 |
| [13] |
PASTOR BEDMAR A. Synchronization processes and synchronizer mechanisms in manual transmissions[J]. International Journal of Advanced Research in Computer Engineering & Technology, 2012, 1(3): 2. |
| [14] |
DOWSON D. A generalized Reynolds equation for fluid-film lubrication[J]. International Journal of Mechanical Sciences, 1962, 4(2): 159. DOI:10.1016/S0020-7403(62)80038-1 |
| [15] |
PATIR N, CHENG H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Tribology, 1978, 100(1): 12. |
| [16] |
PATIR N, CHENG H S. Application of average flow model to lubrication between rough sliding surfaces[J]. Journal of Tribology, 1979, 101(2): 220. |
| [17] |
GREENWOOD J A, TRIPP J H. The contact of two nominally flat rough surfaces[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers 1847-1982 (vols 1-196), 1970, 185(1970): 625. |
| [18] |
GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300. DOI:10.1098/rspa.1966.0242 |
 2019, Vol. 51
2019, Vol. 51


