城市供水系统水量预测分为中长期预测(1~10 a不等)和短期预测(1 h、1 d、1周等)两类.管网用户短期(15 min~1 h)需水量的准确预测是提高供水管网水力模型精度的重要支撑.目前,短期需水量预测常用方法主要有时间序列三角函数法、灰色系统法、小波分析法、积分滑动平均法、Elman神经网络法、广义回归神经网络法、BP神经网络法、支持向量机预测法、最小二乘支持向量机法和贝叶斯最小二乘支持向量机法等[1-6].刘洪波等[1]研究表明采用BP神经网络法的时需水量预测模型,与时间序列三角函数分析法、灰色系统理论预测法、小波分析法的预测模型相比具有预测误差小和计算速度快的优点.陈磊[2]、王亮等[3]基于历史需水量数据建立支持向量机(SVM)的时需水量预测模型,预测结果的平均相对误差(EMAP)为3.38%,与基于BP神经网络的预测模型(EMAP为10.25%)相比预测精度更高,建模速度也更快.陈磊等[4]的研究还证明,基于历史需水量数据以最小二乘支持向量机(LSSVM)法建立的时需水量模型,其预测能力也明显高于基于BP神经网络建立的时需水量模型.何必仕等[5]基于温度、天气、风力、节假日和历史需水量数据,比较了自回归积分滑动平均模型、Elman神经网络、广义回归神经网络以及最小二乘支持向量机法(LSSVM)的时需水量预测模型,结果显示LSSVM模型的需水量预测值EMAP为5.44%,预测精度较高.陈磊与张土乔[6]提出利用贝叶斯置信框架推断最小二乘支持向量机的模型参数,与LSSVM模型相比,时需水量预测模型建模速度更快,预测结果的EMAP为3.59%,优于LSSVM模型的4.83%.
模型预测值与实测值之间都会存在一定的误差(残差),研究表明,采用对需水量预测模型的残差建立残差预测模型,同步修正需水量预测模型的预测值,是一种提高模型预测精度的有效方法.刘大同[7]在进行时间序列预测时,根据残差的混沌特性,对模型的残差建立混沌时间预测模型,对残差进行在线预测进而达到修正模型的预测值、提高模型预测精度的目的.混沌时间序列预测在电力负荷预测方面得到广泛应用,方仍存[8]、雷绍兰[9]、杨卓等[10]根据电力负荷的混沌特性,对电力负荷建立混沌时间序列预测模型,均取得较好的预测效果.
除提高预测模型的精度之外,如何提高预测模型对于不同特点用户的普遍适用性,以及在不同需水工况下的稳定性(需水量变化时)也是需要关注的问题.本文以贝叶斯最小二乘支持向量机法建立了需水量预测模型(BL模型),同时采用贝叶斯最小二乘支持向量机的方法对BL模型预测值与需水量观测值间的残差进行混沌时间序列预测(RM模型),以修正BL模型的预测结果.经实例验证,本文提出的组合预测(BL+RM)模型可显著提高短期(15 min)水量预测模型的精度和稳定性.
1 模型构建的基础理论最小二乘支持向量机(LS-SVM)是标准支持向量机(SVM)的一种扩展[11],LS-SVM与标准SVM的区别主要在于采用不同的优化目标函数,并且用等式约束代替不等式约束.LS-SVM模型的正则化因子和核宽度系数一般常采用交叉验证法、误差界方法和统计方法来确定,容易产生过拟合现象,而且耗时长、计算量大,大大影响了建模的效率和所建模型的性能[12].为此,Mackay[13]提出一种贝叶斯证据框架,已有不少学者将贝叶斯证据框架应用于LS-SVM模型参数的选择[14-15].
1.1 最小二乘支持向量机原理对于给定的输入数据集D=(xi, yi),其中xi∈Rn表示n维输入矢量,xi为第i个输入样本矢量,yi为第i个输出样本标量(i=1, 2…, l),l为样本输入个数,设对样本集进行拟合的函数形式为
| $ y(\boldsymbol{x})=\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b. $ | (1) |
式中:非线性映射φ函数将输入数据映射到一个高维特征空间Rn→Rnh;b为偏执量, ω∈Rnh表示权值向量.为求解y(x),定义目标函数如下:
| $ \begin{array}{l}{\min J\left(\boldsymbol{\omega}, \xi_{i}\right)=\frac{1}{2}\|\boldsymbol{\omega}\|^{2}+\frac{1}{2} \gamma \sum\limits_{i=1}^{l} \xi_{i}^{2}}, \\ {\text { s.t } y_{i}=\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+\xi_{i}}.\end{array} $ | (2) |
式中:γ为正规化参数,ξi为松弛变量.
定义Lagrange函数:
| $ \begin{array}{c}{L\left(\boldsymbol{\omega}, b, \xi_{i}, \alpha_{i}\right)=\frac{1}{2}\|\boldsymbol{\omega}\|^{2}+\frac{1}{2} \gamma \sum\limits_{i=1}^{l} \xi_{i}^{2}-} \\ {\sum\limits_{i=1}^{l} \alpha_{i}\left[\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+\xi_{i}-y_{i}\right]}.\end{array} $ | (3) |
式中:αi为拉格朗日乘子,根据KKT条件:
| $ \begin{array}{l}{\frac{\partial L}{\partial \boldsymbol{\omega}}=0 \rightarrow \boldsymbol{\omega}=\sum\limits_{i=1}^{l} \alpha_{i} \varphi\left(\boldsymbol{x}_{i}\right)}, \\ {\frac{\partial L}{\partial b}=0 \rightarrow b=\sum\limits_{i=1}^{l} \alpha_{i}=0}, \\ {\frac{\partial L}{\partial \xi_{i}}=0 \rightarrow \alpha_{i}=\gamma \cdot \xi_{i}}, \\ {\frac{\partial L}{\partial \alpha_{i}}=0 \rightarrow \boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+\xi_{i}-y_{i}=0}.\end{array} $ | (4) |
消去ω和ξi得到优化问题的解析解
| $ \left[\begin{array}{l}{b} \\ {\boldsymbol{\alpha}}\end{array}\right]=\left[\begin{array}{cc}{0} & {\bf{1}^{\mathrm{T}}} \\ {\bf{1}} & {\boldsymbol{M}+\boldsymbol{\gamma}^{-1} \boldsymbol{I}}\end{array}\right]\left[\begin{array}{l}{0} \\ {y}\end{array}\right]. $ | (5) |
式中:α=[α1, α2, …, αl]T;1为元素取值全为1的1×l维向量,1=[1, 1, …, 1]T;I为l×l维对角线元素全为1的对角阵;M为l×l维方阵,其元素取值满足Mij=φ(xi)T·φ(xj),其中i, j=1, 2, …l.
定义核函数:
| $ K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\exp \left(\frac{-\left\|\boldsymbol{x}_{i}-\boldsymbol{x}\right\|^{2}}{2 \sigma^{2}}\right). $ | (6) |
则采用径向核基函数(RBF)的LS-SVM表达式为
| $ y(\boldsymbol{x})=\sum\limits_{i=1}^{l} \alpha_{i} K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)+b. $ | (7) |
证据框架将贝叶斯推断分为3个准则的推断,每个准则优化LS-SVM的不同参数,准则1利用贝叶斯规则对后验分布密度中的参数进行推断,并通过最大化后验概率来获得参数的估计值,可以推断出权值参数ω最优值;准则2通过最大化正规化参数γ的后验分布来求取正规化参数的最优值;准则3通过最大化后验概率来比较不同模型的优劣,从而选择最优核参数σ[16-17].
准则1推断.令H为模型空间,D为样本训练集,对于给定的超参数λ=1/γ,由贝叶斯规则推断参数向量ω的后验概率为
| $ P(\boldsymbol{\omega} | D, \lambda, H) \propto P(D | \boldsymbol{\omega}, \lambda, H) P(\boldsymbol{\omega} | \lambda, H). $ | (8) |
假设训练样本独立同分布,且参数ω的先验分布P(ω|λ, H)服从正态分布,可得ω的后验概率为
| $ P(\boldsymbol{\omega} | D, \lambda, H) \propto \exp \left(-\frac{1}{2}\|\boldsymbol{\omega}\|^{2}-\sum\limits_{i=1}^{l} \xi_{i}^{2}\right). $ | (9) |
式中:l为训练样本的数目;ξi为LS-SVM对每个训练样本的回归误差;通过最大化式(9)得到ω的最优值ωbest.
准则2推断.通过最大化λ的后验概率P(λ|D, H),即可求得λ的最优值λbest.令
| $ P(\lambda |D, H) \propto \frac{{{{(2{\rm{ \mathsf{ π} }}\lambda )}^{\frac{k}{2}}}\exp \left( { - \lambda E_\omega ^{{\rm{best}}} - E_{\rm{D}}^{{\rm{best}}}} \right)}}{{{{(\det \mathit{\boldsymbol{A}})}^{\frac{1}{2}}}}}. $ | (10) |
式中:Eωbest、EDbest分别为Eω、ED在ωbest处的值,A=∂2(λEω+ED)/∂2ω=∇2(λEω+ED),∇为矢量微分算符,通过最大化lnP(λ|D, H)可得到λ的最优值λbest.
准则3推断.准则3通过检查模型的后验概率P(H|D)∝P(D|H)P(H),对不同模型的优劣进行比较,从而选择最优核参数.假定对于所有模型其先验概率P(H)为平坦分布,则P(D|H)通过对参数λ的积分求得
| $ \begin{array}{c}{P(H | D) \propto \int P(D | \lambda, H) P(\lambda | H) \mathrm{d} \lambda \propto} \\ {P\left(D | \lambda_{\mathrm{best}}, H\right) / \sqrt{\delta}}.\end{array} $ | (11) |
通过最大化lnP(H|D)可得LS-SVM的最优核参数δbest.
1.3 混沌时间序列预测混沌时间序列预测是建立在Takens提出的嵌入定理和相空间重构理论基础上的,其基本思想是系统中的任一分量的演化是由与之相互作用着的其他分量决定的,这些相关分量的信息就隐含在任一分量的发展过程中,可以从仅仅与时间相关的混沌数据中提取和恢复出系统原来的规律,实质上表达为高维空间下的一种轨迹[7].
刘大同[7]、高俊杰[18]、朱志宇等[19]采用SVM对混沌时间序列进行预测,取得了较好的预测效果,但SVM模型存在模型预测精度较低和计算速度慢的缺点[6].本文研究采用贝叶斯优化最小二乘支持向量机法对混沌时间序列进行建模.
贝叶斯优化最小二乘支持向量机在混沌时间序列预测中的依据:混沌序列{e1, e2, …, ek},k为序列总长度,通过曹氏法(C-C法)[18]求得延迟时间τ和嵌入维数m,根据相空间重构原理,进行相空间重构后共有N个相点(N=k-(m-1)τ),依次为
| $ \begin{array}{c} \mathit{\boldsymbol{e}}_{1}=\left\{e_{1}, e_{1+\tau}, e_{1+2 \tau}, \cdots, e_{1+(m-1) \tau}\right\}, \\ \mathit{\boldsymbol{e}}_{2}=\left\{e_{2}, e_{2+\tau}, e_{2+2 \tau}, \cdots, e_{2+(m-1) \tau}\right\}, \\ \vdots \\ \mathit{\boldsymbol{e}}_{N}=\left\{e_{N}, e_{N+\tau}, e_{N+2 \tau}, \cdots, e_{N+(m-1) \tau}\right\}. \end{array} $ | (12) |
进一步演化后的相点eN+1为
| $ \boldsymbol{e}_{N+1}=\left\{e_{N+1}, e_{N+1+\tau}, e_{N+1+2 \tau}, \cdots, e_{N+1+(m-1) \tau}\right\}. $ | (13) |
上式的最后一维元素eN+1+(m-1)τ正是需要预测的下一序列点ek+1.
贝叶斯最小二乘支持向量机在混沌预测中的应用具有两个性质:①某个相点的演化行为与其邻近相点的演化行为类似;②相点ei(i=1, 2, …, N)进一步演化成为ei+1,ei与ei+1最后一维元素ei+1+(m-1)τ之间有某种复杂的函数关系:
| $ e_{i+1+(m-1)_{\tau}}=f\left(\boldsymbol{e}_{i}\right). $ | (14) |
依据这两条性质,找出ei的t个邻近点组成的集合eij(j=1, 2, …, t),再利用贝叶斯优化最小二乘支持向量机的逼近性能,找出一个最优函数来拟合f(*),即
| $ e_{i j+1+(m-1) \tau}=f\left(\boldsymbol{e}_{i j}\right). $ | (15) |
若函数关系f(*)确定,则预测如下:
| $ e_{k+1}=e_{N+1+(m-1)_{\tau}}=f\left(\boldsymbol{e}_{N}\right). $ | (16) |
同理可进行ek+2和ek+3的预测值.
2 用户需水量预测步骤 2.1 模型输入参数选择在短期需水量影响因素的研究方面,信昆仑等[20]进行日需水量预测时,不考虑工作日和休息日的影响,评估了温度、湿度、降水量与城市需水量的相关程度,将温度、湿度作为需水量影响因子建立日需水量预测模型;Bakker[21]、Al-Zahrani等[22]均未考虑工作日和休息日的差异,将温度、湿度和风速作为需水量影响因子建立日需水量预测模型.Brentan等[23]在进行实时(15 min)需水量预测时,考虑了工作日和休息日的影响,通过将温度、湿度、风速、降雨量等物理量与需水量做相关性分析,认为温度、湿度与需水量的相关性程度较高.
本文结合实际数据资料进行了综合分析,认为工作日与休息日在用水特征方面有差异,为提高模型预测的准确度,分别建立了工作日和休息日两种用水模式下的需水量预测模型(BL模型);同时,选取了温度、湿度作为影响需水量变化的影响因子.
为了预测用户在t时刻的需水量Qt,模型建立过程中选取预测日前n d的历史数据训练模型,历史数据记录时间间隔为15 min(采样频率为4次/h即0.25 h/次),选取t时刻(用1, 2, 3, …, 96表示)、温度Tt、湿度Wt,前一个时刻的需水量Qt-1,前1 d该时刻的需水量Qt-96,前一周该时刻的需水量Qt-572(工作日和休息日考虑在一起的需水量预测模型)或Qt-480(工作日需水量预测模型)或Qt-192(休息日需水量预测模型)作为模型的输入,t时刻的需水量Qt作为模型的输出,具体见表 1.
| 表 1 模型的输入变量 Tab. 1 Input variables of the model |
基于贝叶斯最小二乘支持向量机和残差修正的用户短期需水量预测的流程如下:
1) 收集用户需水量历史数据及对应的温度、湿度历史记录,对历史数据中异常、缺失的数据进行处理;
2) 分析用户工作日与休息日需水量变化规律,建立初始化需水量预测模型;
3) 根据在线更新的输入数据xk的观测值及需水量yk,更新贝叶斯最小二乘支持向量机模型训练输入X={xi-1, xi, xi+1, …, xk-1}为X={xi, xi+1, xi+2, …, xk}进行下一步预测,预测值记为yk+1;同时更新混沌时间序列残差预测模型(简称RM模型)输入
4) 通过RM模型和BL模型(简称BL+RM模型)计算第k+1步需水量预测值为ypretict=yk+1-ek+1.
BL+RM模型算法流程如图 1所示,其中RM模型的算法结构示意如图 2所示.

|
图 1 BL+RM模型算法流程 Fig. 1 Flow chart of BL+RM model algorithm |
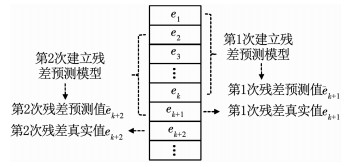
|
图 2 RM模型算法流程 Fig. 2 Flow chart of RM model algorithm |
本文采用相对误差(ER)[3, 7, 21]、平均相对百分误差(EMAP)[3, 5, 21-23]、均方误差(ERMS)[5, 21, 23]、皮尔逊相关系数(R)[5]作为模型预测性能评价指标;ER、EMAP和ERMS的值越小模型预测精度越高;R值衡量两个数据集合的相关度,R越接近于1,两个数据集合相关性越好, 越接近在一条直线上.
| $ E_{\mathrm{R}}=\frac{\left|y_{{\rm o}, i}-y_{\mathrm{m}, i}\right|}{y_{{\rm o}, i}} \times 100 \%, $ | (17) |
| $ {E_{{\rm{MAP}}}} = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_{{\rm{o}}, i}} - {y_{{\rm{m}}, i}}} \right|} }}{{{y_{{\rm{o}}, i}}}} \times 100\% , $ | (18) |
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {\left( {{y_{{\rm{o}}, i}} - {y_{{\rm{m}}, i}}} \right)} }}{n}} . $ | (19) |
式中:yo, i,ym, i分别为时间序列中第i时刻的需水量实测值和预测值,n为时间序列的长度.
3 实例分析为了验证本文方法的有效性,以某大城市的3个小区需水量为例进行了水量预测应用验证.首先收集并处理2017年该市A、B、C 3个小区的入口流量计所记录的每15 min(采样频率为4次/h)的需水量数据(即0.25 h记录一次,每天24 h共记录96个时刻的需水量数据). A、B、C 3个小区有不同的需水量特点,如表 2所示,3个小区的需水量平均周期相同;其中A和B小区平均需水量相近,但需水量随机波动性差别较大;A和C小区的需水量随机波动性相近,但平均需水量有差异,其中C小区平均需水量较大;B和C小区需水量的随机波动性及平均需水量均明显不同.用预测日前30 d的数据来训练模型;在相同时段分别建立上述3个小区工作日和休息日的BL+RM模型预测未来20 d(工作日)、未来10 d(休息日)的需水量.以下以A小区为例,进行具体应用分析说明.
| 表 2 A、B、C 3个小区2017年需水量分析 Tab. 2 Analysis of water demand of three communities (A, B, and C) in 2017 |
考虑到工作日和休息日对用水规律的影响,对A小区的用水规律进行分析如图 3所示,其中横坐标为1 d 24 h内的96个时刻,纵坐标为各时刻的需水量. 表 3为图 3中各标志点的坐标,横坐标为时刻值,纵坐标为需水量.用水规律分析结果如表 4所示.
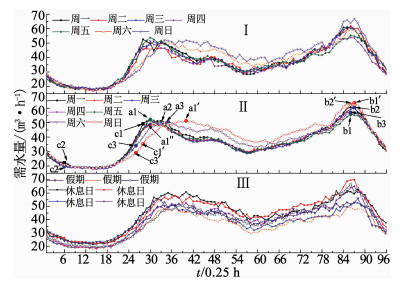
|
图 3 A小区用户用水规律曲线 Fig. 3 Water use regularity curve of community A |
图 3-Ⅰ、图 3-Ⅱ分别为小区7月3—9日的1周需水量变化规律及7月1—28日连续4周对应各时刻需水量进行加权平均后的变化规律.由表 4可知,周一—周日、周一—周五(工作日)、周六—周日(休息日)早高峰出现的最大时间差分别为2.5,1.25和1.25 h,早高峰需水量最大误差分别为6.77%,6.77%,1.64%,分析可得休息日的早高峰与工作日早高峰相比明显不同,最多延迟2.5 h出现;晚高峰出现的最大时间差均为0.25 h,晚高峰需水量最大误差分别为14.15%,12.71%和11.62%,可知休息日的晚高峰与工作日晚高峰在峰值出现时刻及峰值需水量均无明显差别;早高峰和晚高峰时间段外的需水量最大误差分别外为39.81%,12.7%,16.87%,因此,早高峰和晚高峰时间段外休息日需水量明显高于工作日需水量.综上,研究中分别建立工作日和休息日需水量预测模型是正确的.
图 3-Ⅲ为法定节假日与其邻近前后休息日的需水量变化曲线,可以看出,节假日与休息日的用水变化规律相似,早高峰及晚高峰的出现时刻及需水量也均无明显差别,因此,研究中将节假日划分到休息日预测模型中.
3.2 需水量预测模型的建立以A小区预测日前30 d(仅工作日)的历史数据训练初始化的工作日BL模型,预测未来20 d(6月21日—7月20日1个月左右)处于全年需水量高峰时的需水量;并同步对BL模型的残差建立RM模型,修正工作日BL模型预测值.以A小区预测日前30 d(仅休息日和法定节假日)的历史数据训练初始化的休息日需水量预测模型,预测未来10 d(7月16日—8月19日1个月左右)处于全年需水量高峰时的需水量,并同步对BL模型的残差建立RM模型,修正休息日BL模型预测值.
3.3 预测结果分析1) 表 5,6分别为将工作日与休息日考虑在一起、将工作日与休息日分开分别建立BL模型时,工作日、休息日的预测值与实际值相对误差占比.由表 5,6分析可知,将工作日和休息日分开时工作日和休息日BL模型的预测精度与将工作日和休息日考虑在一起时相比,BL模型的预测精度得到显著提高,证实了依据工作日和休息日用水规律不同分别建立工作日和休息日水量预测模型的必要性.
| 表 5 A小区BL模型工作日预测误差占比 Tab. 5 Proportion of the forecast error of the BL model on working days |
| 表 6 A小区BL模型休息日预测误差占比 Tab. 6 Proportion of the forecast error of the BL model on non-working days |
2) 工作日6月21—23日实际需水量、BL模型、BL+RM模型的预测结果如图 4,5,6所示.
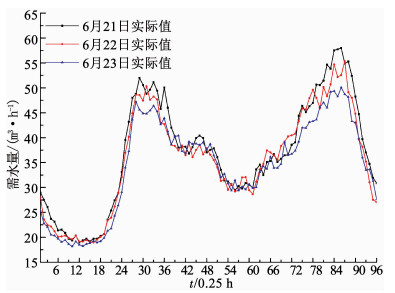
|
图 4 6月21—23日实际需水量 Fig. 4 Actual water demand from June 21 to 23 |

|
图 5 6月21—23日实际需水量与BL模型预测值 Fig. 5 Actual water demand and BL model forecast on working days from June 21 to 23 |

|
图 6 6月21—23日实际需水量与BL+RM预测值 Fig. 6 Actual water demand and BL+RM model forecast on working days from June 21 to 23 |
由图 4可知,6月23日实际需水量较6月21—22日实际需水量有较大波动;分析图 5可知,6月23日BL模型的预测值与实际值之间存在较大的误差;由图 5,6可知,6月23日BL+RM模型的预测精度明显高于BL模型的预测精度.表明BL模型不能快速适应需水量发生较大波动的情况,稳定性较差,而RM模型可以挖掘BL模型系统残差中蕴藏的规律,忽略系统残差背后众多影响因素和复杂的影响机理并预测系统的残差值,修正BL模型的预测值,BL+RM组合模型的稳定性明显较高,对需水量波动较大的用户具有较强的适应能力.
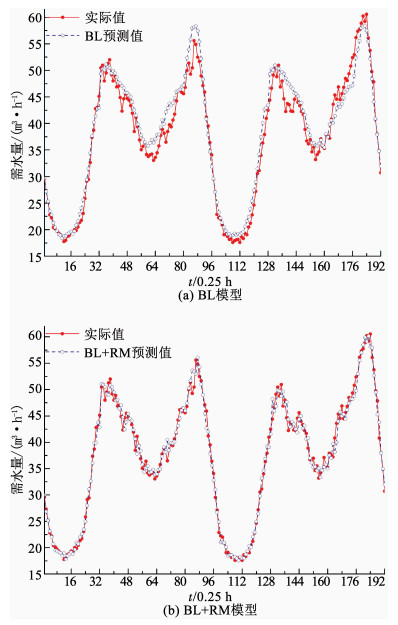
3) 分别随机挑选工作日、休息日BL模型和BL+RM模型连续两天的预测结果,需水量预测值与实际观测值的对比分析如图 7,8所示,其中图 7为工作日BL模型和BL+RM模型连续2 d的预测结果,图 8为休息日BL模型和BL+RM模型连续2 d的预测结果.
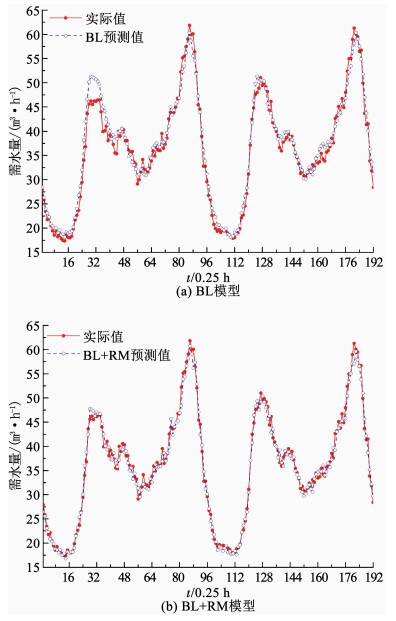
|
图 7 工作日模型预测结果 Fig. 7 Model prediction results on working days |
|
图 8 休息日模型预测结果 Fig. 8 Model forecast results on non-working days |
由图 7(a),(b)及图 8(a),(b)分析可知,BL模型可以准确预测需水量变化的周期性和趋势性,但不能对需水量变化的随机性做出准确的预测,仍存较大的预测残差;通过对BL模型预测值与实际值间的残差建立RM模型,可以精确地捕获预测残差的变化趋势,预测未来的残差值,对BL模型的预测值合理地做出残差补偿,提高需水量预测精度.
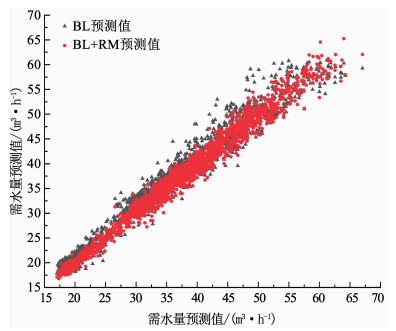
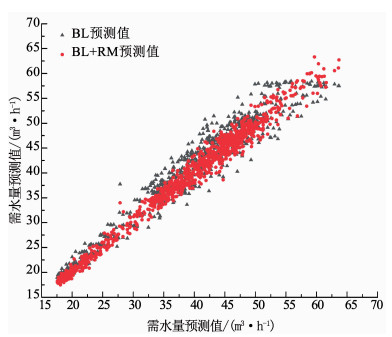
表 7,8分别为A小区工作日连续20 d和休息日连续10 d的预测结果,图 9为工作日连续20 d BL模型和BL+RM模型预测结果与实际值的散点图,图 10为休息日连续10 d BL模型和BL+RM模型预测结果与实际值的散点图.
| 表 7 工作日连续20 d预测结果 Tab. 7 Forecast results for 20 consecutive working days |
| 表 8 休息日连续10 d预测结果 Tab. 8 Forecast results for 10 consecutive non-working days |
|
图 9 工作日连续20 d预测结果散点图 Fig. 9 Scatter plot for 20 consecutive working days prediction |
|
图 10 休息日连续10 d预测结果散点图 Fig. 10 Scatter plot for 10 consecutive non-working days prediction |
由表 7,8可知,与BL模型相比,BL+RM模型可以显著提高需水量预测的精度;图 9,10可以直观地看出,BL+RM模型预测值与实际值之间的离群点数目更少,相关度更高.
4) A、B、C 3个小区BL+RM模型和BL模型预测结果如表 9,10所示.由表 9,10可知,A、B、C 3个小区工作日和休息日的BL+RM模型预测结果ER在10.0%以下的比例均在96.0%以上,EMAP在3.0%左右,模型预测精度较高、精确有效,对多个用户适用性强.
| 表 9 BL+RM模型和BL模型对3个小区工作日连续20 d的预测结果 Tab. 9 20-day forecast results of BL+RM model and BL model on working days of three communities |
| 表 10 BL+RM模型和BL模型对3个小区休息日连续10 d的预测结果 Tab. 10 10-day forecast results of BL+RM model and BL model on non-working days of three communities |
1) RM模型可以准确捕获BL模型预测值残差的变化趋势,修正BL模型的预测值,组合BL模型和RM模型的BL+RM模型具有较高的预测精度.
2) BL+RM组合需水量预测模型具有较高的稳定性,适用于平均水量较小、水量波动较大等不同特点用户的需水量预测.
3) 将工作日和休息日考虑在一起建模时,BL模型的预测精度较低;根据用水规律的特点分别建立工作日、休息日需水量预测模型,可以较大地提高BL模型的预测精度.
| [1] |
刘洪波, 张宏伟, 田林. 人工神经网络法预测时用水量[J]. 中国给水排水, 2002, 18(12): 39. LIU Hongbo, ZHANG Hongwei, TIAN Lin. Artificial neural network method for forecasting hourly water consumption[J]. China Water & Wastewater, 2002, 18(12): 39. DOI:10.3321/j.issn:1000-4602.2002.12.013 |
| [2] |
陈磊, 董志勇. 支持向量机在短期用水量预测中的应用[J]. 浙江工业大学学报, 2007, 35(4): 448. CHEN Lei, DONG Zhiyong. Application of support vector machine to predict short-term water consumption[J]. Journal of Zhejiang University of Technology, 2007, 35(4): 448. DOI:10.3969/j.issn.1006-4303.2007.04.021 |
| [3] |
王亮, 张宏伟, 牛志广. 支持向量机在城市用水量短期预测中的应用[J]. 天津大学学报(自然科学与工程技术版), 2005, 38(11): 1021. WANG Liang, ZHANG Hongwei, NIU Zhiguang. Application of support vector machines in short-term prediction of urban water consumption[J]. Journal of Tianjin University (Science and Technology), 2005, 38(11): 1021. DOI:10.3969/j.issn.0493-2137.2005.11.017 |
| [4] |
陈磊, 张土乔. 基于最小二乘支持向量机的时用水量预测模型[J]. 哈尔滨工业大学学报, 2006, 38(9): 1528. CHEN Lei, ZHANG Tuqiao. Hourly water demand forecast model based on least squares support vector machine[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1528. DOI:10.3321/j.issn:0367-6234.2006.09.031 |
| [5] |
何必仕, 熊晓锋, 蔡华强, 等. 城市供水DMA短期需水量预测比较研究[J]. 杭州电子科技大学学报, 2017, 37(2): 51. HE Bishi, XIONG Xiaofeng, CAI Huaqiang, et al. Comparative study on short-term water demand forecast of urban water supply DMA[J]. Journal of Hangzhou Dianzi University, 2017, 37(2): 51. DOI:10.13954/j.cnki.hdu.2017.02.011 |
| [6] |
陈磊, 张土乔. 基于贝叶斯最小二乘支持向量机的时用水量预测模型[J]. 天津大学学报(自然科学与工程技术版), 2006, 39(9): 1037. CHEN Lei, ZHANG Tuqiao. Hourly water demand forecast model based on Bayesian least squares support vector machine[J]. Journal of Tianjin University (Science and Technology), 2006, 39(9): 1037. DOI:10.3969/j.issn.0493-2137.2006.09.005 |
| [7] |
刘大同.基于Online SVR的在线时间序列预测方法及其应用研究[D].哈尔滨: 哈尔滨工业大学, 2010 LIU Datong. Online SVR based online time series forecasting method and its application[D]. Harbin: Harbin Institute of Technology, 2010 |
| [8] |
方仍存.电力系统负荷区间预测[D].武汉: 华中科技大学, 2008 FANG Naicun. Power system load interval prediction[D]. Wuhan: Huazhong University of Science and Technology, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10487-2009141738.htm |
| [9] |
雷绍兰.基于电力负荷时间序列混沌特性的短期负荷预测方法研究[D].重庆: 重庆大学, 2005 LEI Shaolan. Research on short-term load forecasting based on chaotic characteristics of power load time series[D]. Chongqing: Chongqing University, 2005 http://cdmd.cnki.com.cn/Article/CDMD-10611-2005145198.htm |
| [10] |
杨卓.基于负荷混沌特性和最小二乘支持向量机的短期负荷预测[D].西安: 西安理工大学, 2008 YANG Zhuo. Short-term load forecasting based on chaotic characteristics of load and least squares support vector machine[D]. Xi'an: Xi'an University of Technology, 2008 http://www.cnki.com.cn/Article/CJFDTotal-DWJS200807015.htm |
| [11] |
VAPNIK V N. The nature of statistical learning theory[M]. New York: Spring-Verlag Press, 1995.
|
| [12] |
郑小霞, 钱锋. 基于证据框架的最小二乘支持向量机在精对苯二甲酸生产中的应用[J]. 化工学报, 2006, 57(7): 1612. ZHENG Xiaoxia, QIAN Feng. Application of least squares support vector machine within evidence framework in PTA process[J]. Journal of Chemical Industry and Engineering (China), 2006, 57(7): 1612. DOI:10.3321/j.issn:0438-1157.2006.07.020 |
| [13] |
MACKAY D J C. Probable networks and plausible predictions: A review of practical Bayesian methods for supervised neural networks[J]. Network Computation in Neural Systems, 1995, 6(3): 469. DOI:10.1088/0954-898X_6_3_011 |
| [14] |
阎威武, 常俊林, 邵惠鹤. 一种贝叶斯证据框架下支持向量机建模方法的研究[J]. 控制与决策, 2004, 19(5): 525. YAN Weiwu, CHANG Junlin, SHAO Huihe. Modeling method based on support vector machines within the Bayesian evidence framework[J]. Control and Decision, 2004, 19(5): 525. DOI:10.3321/j.issn:1001-0920.2004.05.010 |
| [15] |
王振树, 李林川, 牛丽. 基于贝叶斯证据框架的支持向量机负荷建模[J]. 电工技术学报, 2009, 24(8): 127. WANG Zhenshu, LI Linchuan, NIU Li. Load modeling based on support vector machine based on Bayesian evidence framework[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 127. |
| [16] |
孙晓东, 陈龙, 杨泽斌, 等. 贝叶斯证据框架下LS-SVM的BPMSM磁链建模[J]. 浙江大学学报(工学版), 2012(5): 873. SUN Xiaodong, CHEN Long, YANG Zebin, et al. Modeling of flux linkage for the BPMSM based on LS-SVM within the Bayesian evidence framework[J]. Journal of Zhejiang University (Engineering Science), 2012(5): 873. DOI:10.3785/j.issn.1008-973X.2012.05.016 |
| [17] |
张弦, 王宏力, 张金生, 等. 状态时间序列预测的贝叶斯最小二乘支持向量机方法[J]. 西安交通大学学报, 2010, 44(10): 42. ZHANG Xian, WANG Hongli, ZHANG Jinsheng, et al. A least squares support vector machine for condition time series prediction based on Bayesian evidence framework[J]. Journal of Xi'an Jiaotong University, 2010, 44(10): 42. DOI:10.7652/xjtuxb201010008 |
| [18] |
高俊杰.混沌时间序列预测研究及应用[D].上海: 上海交通大学, 2013 GAO Junjie. Research and application of chaotic time series prediction[D]. Shanghai: Shanghai Jiaotong University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021728.htm |
| [19] |
朱志宇, 姜长生, 张冰. 基于支持向量回归的混沌序列预测方法[J]. 电工技术学, 2005, 20(6): 57. ZHU Zhiyu, JIANG Changsheng, ZHANG Bing. Prediction of chaotic time series based on support vector regression[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 57. DOI:10.3321/j.issn:1000-6753.2005.06.012 |
| [20] |
信昆仑, 陶涛, 李树平, 等. 考虑气象因子的城市日用水量预测模型[J]. 武汉大学学报(工学版), 2009, 42(4): 461. XIN Kunlun, TAO Tao, LI Shuping, et al. Meteorological factors involved urban water demand forecast model[J]. Engineering Journal of Wuhan University, 2009, 42(4): 461. |
| [21] |
BAKKER M, DUIST H V, SCHAGEN K V, et al. Improving the performance of water demand forecasting models by using weather input[J]. Procedia Engineering, 2014, 70(70): 93. DOI:10.1016/j.proeng.2014.02.012 |
| [22] |
AL-ZAHRANI M A, ABO-MONASAR A. Urban residential water demand prediction based on artificial neural networks and time series models[J]. Water Resources Management, 2015, 29(10): 3651. DOI:10.1007/s11269-015-1021-z |
| [23] |
BRENTAN B M, LUVIZOTTO JR E, HERRERA M, et al. Hybrid regression model for near real-time urban water demand forecasting[J]. Journal of Computational & Applied Mathematics, 2017, 309(C): 532. DOI:10.1016/j.cam.2016.02.009 |
 2019, Vol. 51
2019, Vol. 51


