2. 软弱土与环境土工教育部重点实验室(浙江大学), 杭州 310058
2. MOE Key Laboratory of Soft and Geoenvironmental Engineering (Zhejiang University), Hangzhou 310058, China
近年来, 国内外学者通过现场试验、理论分析、有限元分析等手段, 对楔形桩[1]的承载特性做了大量研究.结果表明, 在相同工况下, 楔形桩与均匀截面的摩擦桩相比, 单位体积承载力提高0.5~2.5倍, 造价降低40%~60%[2].具有良好力学性能的楔形桩现阶段还未能得到广泛应用, 除了制造工艺、运输困难等问题外, 楔形桩的施工质量难以得到可靠的检测也是重要原因.
在现有众多的基桩检测方法中, 低应变反射法检测因其便捷、准确、费用低廉的优点而被广泛接受, 其理论研究已经十分成熟.Novak等[3]导出了多层土体中桩基的波阻抗函数传递规律.Gough等[4]推导出了只考虑桩端土作用时基桩的自由振动特性.Koten等[5]求得了无限长桩在锤击条件下, 考虑桩侧土作用时的纵向振动问题解.王奎华等[6]研究了Voigt土体模型下有限长任意截面桩的解析解问题.陈安国等[7]利用差分法解得基桩在考虑桩土相互作用时的纵向振动响应解.吴文兵等[8~9]对常见完整楔形桩进行了初步理论分析.张献民等[10]研究了桩基缺陷与传递波能量之间的关系.近年来, 王奎华等[11]又提出了考虑竖向作用的桩土模型, 求得了楔形桩桩顶纵向振动解.
以上相关研究成果均是基于等截面管桩建立的, 对楔形桩本身的桩径渐变特性进行了简化处理.因此, 本文基于非等截面桩段划分的基桩模型, 建立振动方程, 利用换元变换, 依次求得桩身振动频域响应和时域响应, 对楔形桩的动力响应展开研究.
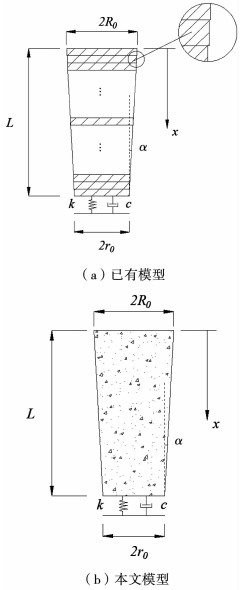
1 方程建立与半解析解楔形桩桩径渐变的几何特性使得桩侧土阻力不仅有切向力, 还存在法向力, 两者共同作用提高了基桩的竖向反力.已有的常见理论模型中, 如图 1(a), 均将桩身划分成足够多的微段, 而其中每个微段都是等截面体, 桩土相互作用直接简化为桩侧竖向阻力, 有些学者考虑了微段底部的竖向反力.但这些假设均与楔形桩实际工作情况不符.对此, 本文提出了新的计算模型, 如图 1(b).
|
图 1 楔形桩计算模型 Fig. 1 Tapered pile calculation model |
所提出的非等截面桩体模型能更好地反映楔形桩受力情况, 考虑已有的理论研究情况, 为方便建立方程, 做出以下合理假设:1)桩为弹性;2)土体采用Winkler模型, 即将桩土作用简化为桩周均布的Voigt体;3)由于桩径越大, 挤土效应越明显, 桩土作用越强, 假设Voigt体的弹性系数、粘壶系数与桩径成正比;4)桩身变形为小变形, 忽略径向变形;5)单层土层内, 土质均匀, 各向同性.
常见的楔形桩如图 1(b)所示, 顶部桩径2R0, 底部桩径2r0, 楔形角α, 桩长L.桩体振动的控制方程为
| $ E\frac{\partial }{{\partial x}}\left( {S\frac{{\partial u}}{{\partial x}}} \right) = \rho S\frac{{{\partial ^2}u}}{{\partial {t^2}}} + {F_{\rm{s}}}. $ | (1) |
式中:u(x, t)表示桩身各处在任意时刻的位移, E为桩身弹性模量, S为桩身截面面积, ρ为桩身材料密度, Fs为桩土相互作用.
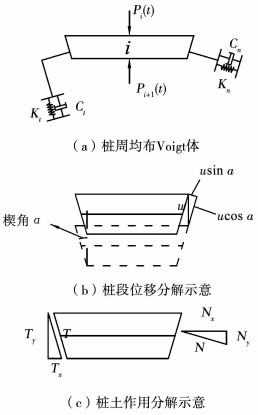
如图 2所示, 观察一个微段的受力情况, 在桩周有均布的法向Voigt体和切向Voigt体, 弹性系数和粘壶系数分别为Kn、Cn、Kt、Ct(Gazetas等[13]和陈鑫[14]对各个系数给出了经验取值).
|
图 2 桩身微段受力分析 Fig. 2 Force analysis of tapered pile |
当此微段发生向下u的位移时, 分解到法向位移为u·sin α, 切向位移为u·cos α.继而可知单位长度桩身受到的法向力N和切向力T:
| $ \begin{array}{l} N = \frac{{2{\rm{ \mathit{ π} }}r}}{{\cos \alpha }}{K_{\rm{n}}}u\sin \alpha + \frac{{2{\rm{ \mathit{ π} }}r}}{{\cos \alpha }}{C_{\rm{n}}}\frac{{\partial u}}{{\partial t}}\sin \alpha = \\ \;\;\;\;\;\;2{\rm{ \mathit{ π} }}r{K_{\rm{n}}}u\tan \alpha + 2{\rm{ \mathit{ π} }}r{C_{\rm{n}}}\frac{{\partial u}}{{\partial t}}\tan \alpha , \end{array} $ | (2) |
| $ \begin{array}{l} T = \frac{{2{\rm{ \mathit{ π} }}r}}{{\cos \alpha }}{K_{\rm{t}}}u\cos \alpha + \frac{{2{\rm{ \mathit{ π} }}r}}{{\cos \alpha }}{C_{\rm{t}}}\frac{{\partial u}}{{\partial t}}\cos \alpha = \\ \;\;\;\;\;2{\rm{ \mathit{ π} }}r{K_{\rm{t}}}u + 2{\rm{ \mathit{ π} }}r{C_{\rm{t}}}\frac{{\partial u}}{{\partial t}}. \end{array} $ | (3) |
其中r为微段平均半径.
将法向力N和切向力T分解到竖向并求和, 即得到单位长度桩身所受桩土作用
| $ \begin{array}{l} {F_{\rm{s}}} = \left( {2{\rm{ \mathit{ π} }}r{K_{\rm{t}}}u + 2{\rm{ \mathit{ π} }}r{C_{\rm{t}}}\frac{{\partial u}}{{\partial t}}} \right) \cdot \cos \alpha + \\ \;\;\;\;\;\;\left( {2{\rm{ \mathit{ π} }}r{K_{\rm{n}}}u\tan \alpha + 2{\rm{ \mathit{ π} }}r{C_{\rm{n}}}\frac{{\partial u}}{{\partial t}}\tan \alpha } \right) \cdot \sin \alpha. \end{array} $ | (4) |
进一步记A=Cntan α·sin α+Ct·cos α, B=Kntan α·sin α+Kt·cos α, 由于Voigt体的弹性系数、粘壶系数与桩径成正比, 变量A、B也即与桩径成正比, 可记A=ar, B=br, 所以有
| $ {F_{\rm{s}}} = 2{\rm{ \mathit{ π} }}{r^2}a\frac{{\partial u}}{{\partial t}} + 2{\rm{ \mathit{ π} }}{r^2}bu. $ | (5) |
式中a、b为比例系数.
代入控制方程式(1)得
| $ E\frac{\partial }{{\partial x}}\left( {S\frac{{\partial u}}{{\partial x}}} \right) = \rho S\frac{{{\partial ^2}u}}{{\partial {t^2}}} + 2{\rm{ \mathit{ π} }}{r^2}a\frac{{\partial u}}{{\partial t}} + 2{\rm{ \mathit{ π} }}{r^2}bu. $ | (6) |
本文中桩底支撑采用Lysmer的经验公式[15]:
| $ k = \frac{{4{\rho _{\rm{s}}}V_{\rm{s}}^2{r_0}}}{{1 - v}}.\;c = \frac{{3.4{\rho _{\rm{s}}}{V_{\rm{s}}}r_0^2}}{{1 - v}}. $ |
式中:Vs为土体剪切波速,
因此, 底部边界条件为
| $ \frac{{\partial u}}{{\partial x}} + \frac{{ku}}{{E{S_{\rm{d}}}}} + {\left. {\frac{c}{{E{S_{\rm{d}}}}}\frac{{\partial u}}{{\partial t}}} \right|_{x = L}} = 0. $ | (7) |
式中Sd为桩底面积.当桩顶施加荷载P(t)时, 形成边界条件为
| $ {\left. {\frac{{\partial u}}{{\partial x}}} \right|_{x = 0}} = - \frac{P}{{E{S_{\rm{t}}}}}. $ | (8) |
其中St为桩顶面积.
1.2 方程解答楔形桩桩径与桩长呈线性关系, 显然有r=R0-xtan α, 即
| $ {\rm{d}}r = - \tan \alpha \cdot {\rm{d}}x. $ | (9) |
对方程(6)进行换元变换, 令u=w/r.代入后得
| $ {v^2}{\tan ^2}\alpha \frac{{{\partial ^2}w}}{{\partial {r^2}}} = \frac{{{\partial ^2}w}}{{\partial {t^2}}} + \frac{{2a}}{\rho }\frac{{\partial w}}{{\partial t}} + \frac{{2b}}{\rho }w. $ | (10) |
式中:v为激振波在桩身内的传播速度,
相应地, 边界条件转换为
| $ \frac{{\partial w}}{{r\partial r}} - \frac{w}{{{r^2}}} + \frac{k}{{E{S_{\rm{d}}}\tan \alpha }}\frac{w}{r} + {\left. {\frac{c}{{E{S_{\rm{d}}}\tan \alpha }}\frac{{\partial w}}{{r\partial t}}} \right|_{r = {r_0}}} = 0. $ | (11) |
| $ \frac{{\partial w}}{{r\partial r}} - {\left. {\frac{w}{{{r^2}}}} \right|_{r = {R_0}}} = - \frac{P}{{E{S_{\rm{t}}}\tan \alpha }}. $ | (12) |
当桩顶施加固定频率的荷载P=P0eiωt, 基桩发生同频的受迫振动, 桩身各处位移为u=Ueiωt, 变量w=Weiωt, 式中U、W均为与桩身深度(桩径)相关的变量.
式(10)化简为
| $ {v^2}{\tan ^2}\alpha \frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{r^2}}} = \left( { - {\omega ^2} + {\rm{i}}\omega \frac{{2a}}{\rho } + \frac{{2b}}{\rho }} \right)W. $ | (13) |
令
| $ W = {D_1}\exp ({\rm{i}}\lambda r) + {D_2}\exp ( - {\rm{i}}\lambda r). $ | (14) |
式中D1与D2为待求的中间变量.
代入底部边界条件, 得到D1与D2的关系:
| $ \frac{{{D_1}}}{{{D_2}}} = \frac{{{\rm{i}}\lambda - \left( {\frac{{{Z_0}}}{{ES\tan \alpha }} - \frac{1}{r}} \right)}}{{{\rm{i}}\lambda + \left( {\frac{{{Z_0}}}{{ES\tan \alpha }} - \frac{1}{r}} \right)}}{{\rm{e}}^{ - 2{\rm{i}}\lambda r}}. $ | (15) |
式中Z0=k+ciω, 再代入顶部边界条件, 得
| $ \frac{{{\rm{i}}\lambda R - 1}}{{{R^2}}}{{\rm{e}}^{{\rm{i}}\lambda R}}{D_1} - \frac{{{\rm{i}}\lambda R + 1}}{{{R^2}}}{{\rm{e}}^{ - {\rm{i}}\lambda R}}{D_2} = - \frac{{{P_0}}}{{E{S_{\rm{t}}}\tan \alpha }}. $ | (16) |
联立式(15)、(16)可得中间变量D1与D2.
而桩顶振动位移响应为
| $ u = {\left. {U{{\rm{e}}^{{\rm{i}}\omega t}}} \right|_{r = {R_0}}} = \frac{{{D_1}\exp \left( {{\rm{i}}\lambda {R_0}} \right) + {D_2}\exp \left( { - {\rm{i}}\lambda {R_0}} \right)}}{{{R_0}}}{{\rm{e}}^{{\rm{i}}\omega t}}. $ | (17) |
求导得桩顶速度响应:
| $ V = \frac{{{D_1}\exp \left( {{\rm{i}}\lambda {R_0}} \right) + {D_2}\exp \left( { - {\rm{i}}\lambda {R_0}} \right)}}{{{R_0}}}{\rm{i}}\omega {{\rm{e}}^{{\rm{i}}\omega t}}. $ | (18) |
幅值为
| $ {H_{\rm{v}}} = \frac{{{D_1}\exp \left( {{\rm{i}}\lambda {R_0}} \right) + {D_2}\exp \left( { - {\rm{i}}\lambda {R_0}} \right)}}{{{R_0}}}{\rm{i}}\omega . $ | (19) |
即得到了桩顶纵向振动速度频域响应.当在桩顶施加半正弦脉冲
| $ v(t) = {\mathscr{F}^{ - 1}}\left[ {{H_{\rm{v}}}({\rm{i}}\omega ) \cdot P({\rm{i}}\omega )} \right]. $ | (20) |
通过控制变量法验证本文模型的合理性, 以下计算中若不作特殊说明, 楔形桩参数设置为桩长L=10 m, 楔角α=2°, 桩顶半径R0=0.6 m.
2.1 本文退化等截面管桩模型对比通过以上解析过程可知, 在非等截面桩体模型中, 若取楔角为0°, 则楔形桩将退化为等截面管桩.而对于等截面管桩动力响应的研究已经非常成熟[6].因此, 首先就此退化模型进行对比, 其余变量保持一致.
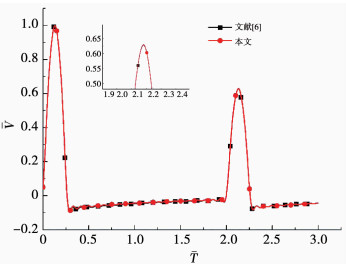
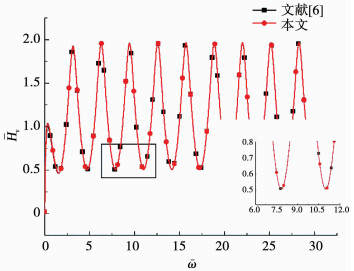
由图 3, 4可知, 本文模型楔角取0°(为保证计算收敛, 计算过程中取值为0.01°)时, 楔形桩退化为等截面管桩, 与已有成熟解相比, 其时域响应和频域响应完全重合, 即验证了本文模型建立的合理性.
|
图 3 退化等截面管桩模型的时响曲线对比 Fig. 3 Comparison of time domain response of degenerated model on pipe pile |
|
图 4 退化等截面管桩模型的频响曲线对比 Fig. 4 Comparison of frequency domain response of degenerated model on pipe pile |
如上所述, 已有的理论分析均将楔形桩简化为多个薄等截面桩段的组合, 吴文兵[9]认为, 当桩身分段高度小于基桩整长的1/100或者更小时, 桩顶动力响应稳定收敛, 为方便表述, 记此类模型为Model 1.本文提出的非等截面桩体模型考虑了桩周土的法向作用, 并真实解答了波在楔形体中的传播, 记为Model 2.针对两种模型的异同, 需要就楔形角和桩周土两个因素展开讨论比较.
考虑到常见楔形桩的楔形角小于2°, 又由《铁路工程抗震设计规范》(GB50111—2006)知地基土剪切波速可高达500 m/s.因此, 在保证其他参数一致的基础上, 设置以下若干对照工况, 如表 1, 2所示.
| 表 1 两种模型在不同楔角下的计算应用 Tab. 1 Computational application of two models under different cone angles |
| 表 2 两种模型在不同土体剪切波速下的计算应用 Tab. 2 Computational application of two models with different soil shear wave velocities |
计算结果比较如图 5, 6.由图 5可以看出, 随着楔形角增大, 时响曲线和频响曲线相应发生变化, 但对于小楔形角桩和大楔形角桩, 两个模型的计算结果均基本重合.一方面, 验证了本文模型的正确性, 另一方面可以看出, 在此工况, Model 1的简化方法在足够的划分层数下可以确保计算精度.

|
图 5 楔形角对模型计算结果的影响 Fig. 5 Influence of cone angle on results of two models |

|
图 6 土质对模型计算结果的影响 Fig. 6 Influence of soil on results of two models |
观察图 6可知, 当土质较差, 地基土剪切波速较小时, 两个模型得到的时响曲线和频响曲线基本一致.但当地基土剪切波速较大时, 曲线反映出的差别比其他工况更为明显.从时域响应看, Model 2的桩底反射低于Model 1, 从频域响应看, Model 2计算曲线的震荡幅度小于Model 1.这是由于随着土体剪切波速提高, 桩土作用增强, 土体对桩身的法向作用得到强化, 导致桩身振动被抑制, 激振波在传递过程中的损耗也增加.在响应曲线上即表现为峰值的降低.
3 楔形桩的几何参数分析与等截面管桩不同, 楔形桩的一大特点就是变桩径, 为了更好地描述楔形桩的几何特征, 抽象出桩长L、桩身半长处桩径Rm、楔角α 3个特征参数.主要研究楔形桩的几何尺寸对桩顶动力响应的影响, 因此, 设定土体为均质土.
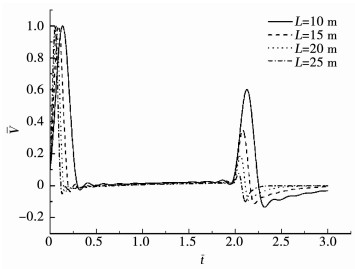
改变桩长L, 参数Rm=0.5 m, α=2.5°, 计算得到图 7, 8.可以看出, 当桩长增加时, 时响曲线的桩底反射高度逐渐降低至0, 此例中, 当桩长为20 m时, 桩底反射已经不明显, 而桩底反射信号前的区域几乎不受影响.除此之外频响曲线的震荡幅度也随之减小, 同阶共振频率发生一定的偏移.这是由于楔形桩的桩长增大时, 桩土相互作用加强, 使得初始激振波在传递过程中发生了更多损耗, 因此, 桩底反射信号会减小, 而频响曲线反映的是某频率下的共振速度幅值, 也因桩土作用的增强而受到抑制.
|
图 7 桩长对楔形桩时域响应的影响 Fig. 7 Influence of pile length on time domain response |

|
图 8 桩长对楔形桩频域响应的影响 Fig. 8 Influence of pile length on frequency domain response |
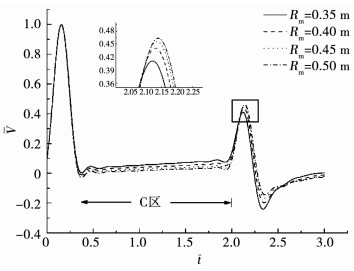
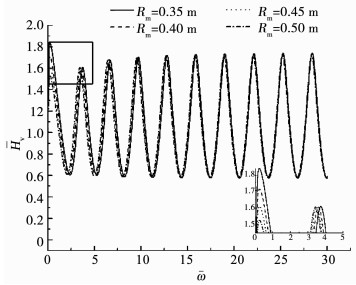
改变桩身半长处桩径Rm, 参数L=10 m, α=2.5°, 得到图 9, 10.可以看出, 当Rm增加时, 时响曲线中桩底反射信号会产生较小的增幅, 桩底反射信号前的曲线段(以下记为“C区”)会随之下沉.这是由于当Rm增大时, 桩截面的面积和周长随之增加, 截面积控制了桩身内部作用力, 截面周长控制了桩土相互作用, 其增幅小于截面积的增幅, 因而桩土作用会相对减小.另外, 由于楔形桩桩径渐变, 对于一定长度的桩段, 上下截面的波阻抗不同, 导致激振波在传递过程中会逐渐反射至桩顶, 在时响曲线中反映为C区曲线的上抬.当Rm增大时, 桩段上下截面的波阻抗差相对减小, 因而C区曲线会随之下沉.对于频响曲线, Rm的增大会导致低频段曲线的震荡幅度减小, 对高频段曲线的影响不大.
|
图 9 Rm对楔形桩时域响应的影响 Fig. 9 Influence of Rm on time domain response |
|
图 10 Rm对楔形桩频域响应的影响 Fig. 10 Influence of Rm on frequency domain response |
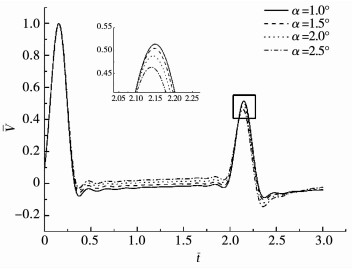
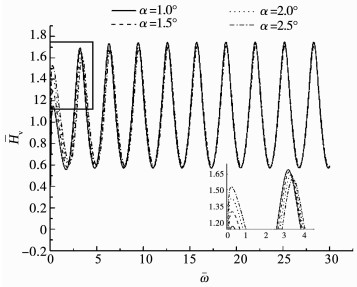
改变楔角α, 参数L=10 m, Rm=0.5 m, 得到图 11, 12.可以看出, 当楔角增大时, 桩底反射信号会小幅降低, 但影响不大.而C区曲线段则会发生明显上升.这是由于楔角的增大, 会导致桩段上下截面间的波阻抗差增大, 导致激振波在达到桩底之前, 有更多能量已经反射至桩顶, 桩底接收能量相应减小, 因而C区上升, 桩底信号下降.另一方面, 随着楔角的增大, 低频区的频响曲线震荡幅度增大, 高频区曲线几乎不受影响.
|
图 11 楔角对楔形桩时域响应的影响 Fig. 11 Influence of cone angle on time domain response |
|
图 12 楔角对楔形桩频域响应的影响 Fig. 12 Influence of cone angle on frequency domain response |
与等截面管桩相同的是, 桩身纵波速对桩顶振动速度响应会产生明显的影响.当前工程应用中, 预制混凝土桩的弹性模量为20~40 GPa, 因而分析中纵波速取值为3 000~4 000 m/s.
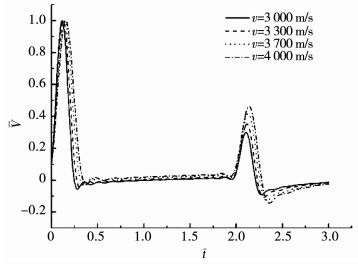
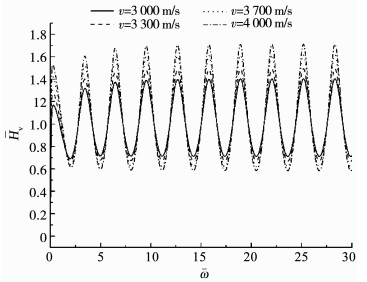
由图 13, 14可知, 随着桩身纵波速提高, 桩底反射信号增强.这是因为纵波速的提高, 意味着桩身弹性模量的增加, 一方面会使得相同外力作用下桩身位移减小, 另一方面, 桩身内部挤压作用相对增大, 桩土相互作用相对减小, 因此, 桩底反射信号会增强.同时, 在频域曲线上, 震荡幅度会变大, 但同阶共振频不发生变化.考虑到当前低应变动测法的应用中, 桩底反射信号能提供桩长、桩身完整性等有效信息, 这意味着, 桩身纵波速(弹性模量)越大, 低应变动测法的检测范围越大.
|
图 13 纵波速对楔形桩时域响应的影响 Fig. 13 Influence of compressional velocity on time domain response |
|
图 14 纵波速对楔形桩频域响应的影响 Fig. 14 Influence of compressional velocity on frequency domain response |
1) 提出了非等截面桩体模型计算楔形桩的纵向振动响应, 通过换元变化得到半解析解.与传统简化的计算模型相比, 当土质较差、地基土剪切波速较小时, 两个模型的计算结果相近, 随着土体剪切波速增大, 两者出现显著差别, 本文模型计算得到的桩顶纵向振动速度要低于简化模型.
2) 抽离出桩长L、桩身半长处桩径Rm、楔角α 3个参数描述楔形桩的几何性质.对比计算表明, 桩长越长, 桩底反射信号越弱, 频响曲线中的震荡幅度越小.另外, 随着Rm增大, α减小, 桩底反射信号会小幅上升, C区曲线会显著下沉, 低频区频响曲线随之增大, 对高频区频响曲线影响不大.
3) 桩身纵波速(弹性模量)会显著影响桩顶振动速度响应.桩身纵波速(弹性模量)越大, 桩底反射信号越强, 频响曲线的振动幅度越大.
| [1] |
徐祖元. 锥形桩的使用经验[J]. 建筑技术, 1980(2): 53. XU Zuyuan. Usage experience of taper pile[J]. Architecture Technology, 1980(2): 53. |
| [2] |
刘杰, 何杰, 闵长青. 楔形刚性桩与桩周土的非线性相互作用[J]. 铁道学报, 2010, 32(2): 137. LIU Jie, HE Jie, MIN Changqing. Nonlinear interaction between the rigid taper pile and pile-surrounding soil[J]. Journal of the China Railway Society, 2010, 32(2): 137. DOI:10.3969/j.issn.1001-8360.2010.02.024 |
| [3] |
NOVAK M, ABOUL-ELLA F. Impedance functions of piles in layered media[J]. Journal of the Engineering Mechanics Division, 1978, 104(3): 643. |
| [4] |
GOUGH W, RICHARD J P G, WILLIAMS R P. Vibration and waves[M]. Halsted Press of John Wiley & Sons, 1983.
|
| [5] |
KOTEN H V, MIDDENDORP P, BREDERODE P V. An analysis of dissipative wave propagation in a pile[C]// International Seminar on the Application of Stress Wave Theory on Piles. Stockholm: Publisher A A, 1980
|
| [6] |
王奎华, 谢康和, 曾国熙. 有限长桩受迫振动问题解析解及其应用[J]. 岩土工程学报, 1997, 19(6): 27. WANG Kuihua, XIE Kanghe, ZENG Guoxi. Analytical solution to vibration of finite length pile under exciting force and its application[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(6): 27. DOI:10.3321/j.issn:1000-4548.1997.06.007 |
| [7] |
陈安国, 刘东甲. 基桩低应变检测的波动方程法数值计算[J]. 合肥工业大学学报(自然科学版), 2007, 30(10): 1336. CHEN Anguo, LIU Dongjia. Numerical computation of the wave equation for low strain test piles[J]. Journal of Hefei University of Technology, 2007, 30(10): 1336. DOI:10.3969/j.issn.1003-5060.2007.10.027 |
| [8] |
吴文兵, 王奎华, 武登辉, 等. 考虑横向惯性效应时楔形桩纵向振动阻抗研究[J]. 岩石力学与工程学报, 2011(增刊2): 3618. WU Wenbing, WANG Kuihua, WU Denghui, et al. Study of dynamic longitudinal impedance of tapered pile considering lateral inertial effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(Suppl 2): 3618. |
| [9] |
吴文兵, 王奎华, 窦斌. 任意层地基中粘弹性楔形桩纵向振动响应研究[J]. 振动与冲击, 2013, 32(8): 120. WU Wenbing, WANG Kuihua, DOU Bin. Vertical dynamic response of a viscoelastic tapered pile embedded in layered foundation[J]. Journal of Vibration and Shock, 2013, 32(8): 120. DOI:10.3969/j.issn.1000-3835.2013.08.021 |
| [10] |
张献民, 蔡靖, 王建华. 基桩缺陷逐步能量恢复递推定量分析[J]. 岩土力学, 2003(增刊2): 481. ZHANG Xianmin, CAI Jing, WANG Jianhua. Quantitative recurrence analysis to determine defects of piles by energy recovery method[J]. Rock and Soil Mechanics, 2003(Suppl 2): 481. |
| [11] |
李强, 王奎华. 成层饱和土中桩纵向振动特性研究及应用[J]. 工程力学, 2007, 24(10): 144. LI Qiang, WANG Kuihua. A study on longitudinal pile vibration in saturated layered soil and its application[J]. Engineering Mechanics, 2007, 24(10): 144. DOI:10.3969/j.issn.1000-4750.2007.10.025 |
| [12] |
VELEZ A, GAZETAS G, KRISHNAN R. Lateral dynamic response of constrained-head piles[J]. Journal of Geotechnical Engineering, 1983, 109(8): 1063. DOI:10.1061/(ASCE)0733-9410(1983)109:8(1063) |
| [13] |
陈鑫.带承台单桩纵向振动特性研究[D].杭州: 浙江大学, 2014 CHEN Xin. Study on the vertical dynamic characteristics of single pile with cushion cap[D]. Hangzhou: Zhejiang University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10335-1014171043.htm |
| [14] |
LYSMER J, JR F E R. Dynamic response of footings to vertical loading[J]. Geotechnical Special Publication, 1966, 92(118): 1091. |
 2019, Vol. 51
2019, Vol. 51


