2. 四川省交通运输厅公路规划勘察设计研究院, 成都 610041
2. Sichuan Provincial Transport Department, High Way Planning, Survey, Design and Research Institute, Chengdu 610041, China
剪切滑动破坏是危岩体崩塌中一种常见的破坏模式,较多学者对该类破坏模式下的危岩体稳定性状态评价开展了研究.冯树荣等[1]提出了具有2组平行节理岩质斜坡的极限平衡方法;王林峰等[2]基于材料力学与断裂力学建立了缓倾岩质边坡三维稳定性计算方法.现阶段对危岩体失稳破坏的评价中,大多数研究是基于稳定性系数高低开展的,这种确定性的计算方法常忽略岩质斜坡系统中的不确定因素,所得评价结果多为一种等效均质角度的问题表征,不代表该破坏模式下的危岩体在可变因素影响下的真实状态.针对该类危岩体几何边界参数与结构面参数的不确定性,可靠度理论被逐步用于其稳定性状态的评价当中,该方法能够有效考虑参数存在的不确定性,并以概率的形式评价其实际稳定性状态.因此,开展滑动破坏模式下的危岩体稳定可靠度分析研究尤为重要.
目前,考虑参数不确定性的岩质斜坡可靠度分析较多[3-5].张硕等[6]通过野外调查与概率统计方法研究了滑动破坏的危岩体几何参数与主控结构面等效强度参数的不确定性,并提出了该类危岩稳定可靠度的评价方法;杨智翔等[7]基于可靠度理论研究发现,影响危岩稳定可靠度的主导因素为主控结构面倾角,结构面等效抗剪强度次之.已有研究对于由结构面控制的滑动破坏危岩可靠度分析意义较大,但研究者多基于危岩体几何参数或结构等效强度参数的不确定性进行研究,并未充分考虑结构面实际连通率、贯通段与未贯通段强度、危岩所受作用力参数的不确定性,且考虑断续结构面及作用力参数不确定性的危岩可靠度分析方法未见报道,故有必要对此开展深入研究.
本文以断续结构面控制的单面滑动危岩体为研究对象,选取断续结构面参数与危岩所受作用力参数为随机变量,提出该类危岩体的稳定可靠度分析方法,并结合实际工程案例对该方法进行验证.
1 断续结构面控制的危岩可靠度计算方法危岩体断续结构面的几何参数与强度参数均具备不确定性,其在不同环境中呈现出的分布状态有所差异,故为准确计算目标可靠度需选择适用的模拟方法.蒙特卡罗法不受随机变量是否呈正态、状态函数是否非线性等条件的限制,在满足模拟样本数量的前提下便可算得较为精确的失效概率与可靠度指标.本文基于该方法建立断续结构面控制的危岩体稳定可靠度计算方法.
1.1 危岩体稳定极限状态方程确立利用等效思想,将危岩体受控的断续结构面视为贯通状态,不仅违背了实际地质模型结构,对危岩体稳定可靠度的分析也会造成较大误差,因此,将该类危岩体力学模型中起控制作用的结构面概化为断续状(图 1).图中AB为断续主控结构面;lr为结构面未贯通段总长,lj为结构面贯通段总长,结构面连通率即为η=lj/(lr+lj);α为危岩破裂面倾角;H为危岩体高度;W为危岩体自重;Q为水平地震力,取ξ为水平地震系数,则Q=ξ×W,式中ξ取0.05;V为结构面贯通段中的裂隙水压力,V=0.5γwhw2,式中γw为水的重度,hw为裂隙充水高度,天然工况取贯通段裂隙深度的1/3,暴雨工况取贯通段裂隙深度的2/3.将W、Q、V三力沿断续结构面方向分解为法向分力与切向分力,并以此求得结构面的正应力σn与剪应力τn分别为

|
图 1 断续结构面控制的危岩体模型 Fig. 1 Model of unstable rock masses with discontinuous structures |
| $ {\sigma _n} = (W\cos \alpha - Q\sin \alpha - V)\sin \alpha /H, $ | (1) |
| $ {\tau _n} = (W\sin \alpha + Q\cos \alpha )\sin \alpha /H. $ | (2) |
胡波等[8]基于结构面法向方向的平衡条件,代入Mohr-Coulomb和Patton强度公式得出断续主控结构面的抗剪强度为
| $ {\tau _f} = (1 - \eta )\left( {{c_r} + {\sigma _r}\tan {\varphi _r}} \right) + \eta \left( {{c_j} + {\sigma _j}\tan {\varphi _j}} \right). $ | (3) |
式中:cr与φr分别为断续结构面未贯通段的黏聚力与内摩擦角;cj与φj分别为断续结构面贯通段的黏聚力与内摩擦角;σr与σj分别为其未贯通段与贯通段的正应力.
由结构面法向方向变形协调条件得
| $ \left\{ \begin{array}{l} {\sigma _r} = \frac{E}{{\eta h{K_n} + E(1 - \eta )}}{\sigma _n}, \\ {\sigma _j} = \frac{{h{K_n}}}{{\eta h{K_n} + E(1 - \eta )}}{\sigma _n}. \end{array} \right. $ | (4) |
式中:E为岩石的弹性模量;Kn为断续结构面贯通段的法向刚度;h为危岩体重心到断续结构面的距离.
将式(1)代入式(4)得
| $ \left\{ \begin{array}{l} {\sigma _r} = \frac{{E\sin \alpha (W\cos \alpha - Q\sin \alpha - V)}}{{H\left[ {\eta h{K_n} + E(1 - \eta )} \right]}}, \\ {\sigma _j} = \frac{{h{K_n}\sin \alpha (W\cos \alpha - Q\sin \alpha - V)}}{{H\left[ {\eta h{K_n} + E(1 - \eta )} \right]}}. \end{array} \right. $ | (5) |
将式(5)代入式(3)得
| $ \begin{array}{l} {\tau _f} = (1 - \eta )\left\{ {{c_r} + \frac{{E\tan {\varphi _r}\sin \alpha (W\cos \alpha - Q\sin \alpha - V)}}{{H\left[ {\eta h{K_n} + E(1 - \eta )} \right]}}} \right\} + \\ \eta \left\{ {{c_j} + \frac{{h{K_n}\tan {\varphi _j}\sin \alpha (W\cos \alpha - Q\sin \alpha - V)}}{{H\left[ {\eta h{K_n} + E(1 - \eta )} \right]}}} \right\}. \end{array} $ | (6) |
在不考虑变量间相关性的条件下视危岩几何尺寸为定量,引入η、cr、cj、φr、φj、Q、V及W 8个随机变量,设定主控结构面抗剪强度τf与剪应力τn的综合基本变量分别为R(η, cr, cj, φr, φj, Q, V, W)与S(Q, W).同时,结合滑塌式危岩稳定极限状态的定义可知,当主控结构面抗剪强度与剪应力的比值为1时,危岩体处于极限平衡状态,则断续结构面主控下的危岩体极限状态方程为
| $ \begin{array}{l} Z(x) = Z\left( {\eta , {c_r}, {c_j}, {\varphi _r}, {\varphi _j}, Q, V, W} \right) = \\ \;\;\;\;\;\;\;\;\;\;\frac{{R\left( {\eta , {c_r}, {c_j}, {\varphi _r}, {\varphi _j}, Q, V, W} \right)}}{{S(Q, W)}} - 1.0 = 0. \end{array} $ | (7) |
当Z<0时,危岩体处于失稳破坏状态,根据式(7)建立断续结构面主控下的危岩体稳定可靠度功能函数为
| $ \begin{array}{l} Z(x) = Z\left( {\eta , {c_r}, {c_j}, {\varphi _r}, {\varphi _j}, Q, V, W} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;Z\left( {{x_1}, {x_2}, {x_3}, {x_4}, {x_5}, {x_6}, {x_7}, {x_8}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{R\left( {{x_1}, {x_2}, {x_3}, {x_4}, {x_5}, {x_6}, {x_7}, {x_8}} \right)}}{{S\left( {{x_6}, {x_8}} \right)}} - 1.0 <0. \end{array} $ | (8) |
式中:x1,x2,x3,x4,x5,x6,x7,x8分别表示变量η,cr,cj,φr,φj,Q,V,W.
基于蒙特卡罗法模拟,设置N次抽样,并利用功能函数中8个变量参数初始分布的联合概率密度函数fx1,x2,…,x8(x1,x2,…,x8)生成随机样本xi,将危岩体的失稳概率Pf表示为
| $ {P_f} = \mathop \smallint \limits_{Z(x) \le 0} \prod\limits_{i = 1}^N f {x_i}\left( {{x_i}} \right){\rm{d}}x = {E_{f{x_i}\left( {{x_i}} \right)}}\left\{ {I[Z(x)]} \right\}. $ | (9) |
式中:I[Z(x)]为指示函数,I[Z(x)]于Z(x)≤0时取1,Z(x)>0时取0;E[·]为在联合概率密度函数下的数学期望算子[9].
通过对联合概率密度函数中8个随机变量样本的抽取,计算出每组样本对应的Z(x)数值,即获得危岩体的失稳样本(Z(x)<0)个数,利用失稳样本的均值将失稳概率Pf的一个估计值表示为
| $ {\hat P_f} = \frac{1}{N}\sum\limits_{i = 1}^N I \left[ {Z\left( {{x_i}} \right)} \right] = \frac{{{n_s}}}{N}. $ | (10) |
式中ns为失稳样本个数.
可靠度指标β是表征失稳概率的一种度量,其与危岩失稳概率具备一一对应关系,β越大,危岩失稳概率越小,反之Pf则越大.β绝对值的大小可反映危岩体的稳定可靠程度,当β为正值且较大时,表明危岩体较稳定可靠;当β为负值且绝对值较大时,危岩体破坏的可能性极大[10].其与Pf相对应为
| $ \beta = \frac{{{\mu _Z} - 1}}{{{\sigma _Z}}} = - {\varphi ^{ - 1}}\left( {{{\hat P}_f}} \right). $ | (11) |
式中φ为标准正态分布函数.
2 多因素对应可靠度的敏感性分析基于正交试验设计,以危岩失稳概率和断续结构面相关变量因素为研究对象,假定各因素变异系数均为一相同定值,计算分析各参数均值对应失稳概率的敏感性大小及其随各均值变化的规律.正交试验设计是用于多因素试验的一种方法,是从全面试验中挑选出部分有代表的点进行试验,这些代表点具有均匀和整齐的特点[11].其可以通过部分代表性试验的分析结果来掌握全面试验的效果,且计算过程简便,具有较高效率.
正交试验设计中,将各组试验得到的结果称作指标,将所研究的各项影响指标的试验成分称作因素,因素在试验中要比较的不同条件称作水平.本文选用极差分析法来考察试验结果,各因素的极差计算公式如下:
| $ {R_j} = \max \left\{ {{K_{ij}}} \right\} - \min \left\{ {{K_{ij}}} \right\}. $ | (12) |
式中Kij为j因素的第i个水平获得的试验结果总和.
极差越大,表明因素水平的改变对试验结果的影响越显著,即极差最大的因素为主导因素,次大的因素为次主导因素,依次排列可得各因素对应试验指标的敏感性顺序.
3 主导因素参数变异性对可靠度的影响规律利用响应面设计与方差分析法,分析主导因素与次主导因素的参数变异性对危岩失稳概率的影响,同时考察二者均值的变化对变异系数响应程度的影响规律.响应面设计是根据系统变量参数多种组合的试验结果,通过最小二乘法回归拟合出变量参数与分析目标之间响应面函数的试验方法[12].该方法可以有效地减少试验次数,通过方差分析得出各研究因素影响试验指标的显著性大小,且能够通过三维响应面图直观地反映出研究因素间的交互关系.选用二阶多项式构建响应面函数模型:
| $ \hat y = A + \sum\limits_{i = 1}^k {{B_i}} {x_i} + \sum\limits_i {\sum\limits_j {{C_{ij}}} } {x_i}{x_j} + \sum\limits_{i = 1}^k {{D_{ii}}} x_i^2. $ | (13) |
式中:xi, j(i, j=1,2,…,n)为随机变量;A,Bi,Cij,Dii(i, j=1,2,…,n)为待定因子.
基于已构建的响应面模型,对变量组合的多组试验指标进行统计,随后进行模型显著性验证与方差分析(ANOVA).模型回归方差中变量对危岩失稳概率影响的显著性由95%置信度的联合假设检验判断.其中,F值表示方程中各变量影响响应指标的显著性;P值是指某事件发生概率的大小[13],变量显著程度随概率P值的减小而增高,当P<0.05时变量为显著,当P<0.01时变量为极显著.所做试验与模型拟合的程度由模型P值、失拟项P值及确定系数R2表示,当模型P<0.01、失拟项P>0.05及R2>0.8[14]均满足时,二者能够较好拟合,所得分析结论也更为可靠.
4 工程实例分析 4.1 危岩体稳定可靠度计算南门湾危岩带位于重庆市巫溪县新老县城之间,该处于1987年开始,多次发生岩体失稳崩塌,并时常伴有局部掉块现象,对当地通往周围地区的道路交通及人员安全造成了巨大隐患,严重制约了巫溪县的社会经济发展[15].危岩带主要由三叠系嘉陵江组白云质角砾状石灰岩组成,由北到南沿180°~130°方向呈弧形展布,全长630 m,北高南低,变形破坏(松动带)宽度4~25 m,垂直斜坡厚度2~14 m.危岩带共存在20处危岩体,除WY1外,WY2~WY20均为由断续结构面控制的危岩体.为验证上述可靠度计算方法的工程适用性,选取暴雨工况下的4个代表性危岩体(WY5、WY7、WY10、WY12)进行可靠度计算与稳定性状态评价.
首先,通过野外调查、室内试验、原位测试及相关工程经验,对四者的尺寸定量参数、断续结构面及作用力随机变量参数进行20次统计(表 1),并采用概率图法分析得知该8变量均服从正态分布.利用数值分析软件MATLAB,产生N=1×106个随机样本,计算其稳定可靠度,其中岩石的弹性模量E=35 GPa、断续结构面贯通段的法向刚度Kn=5.2×107 kN/m.其次,仅以结构面等效强度参数为随机变量,基于加权平均法统计计算出四者结构面等效强度参数的均值与标准差,结合文献[16]所提出的滑塌式危岩体可靠度计算方法计算四者的可靠度.最终,利用结构面等效强度参数的均值,通过危岩稳定性评价标准[17]计算出四者的稳定性系数.
| 表 1 危岩体变量参数统计 Tab. 1 Statistics of variable parameters of unstable rock |
如表 2所示,本文方法算得WY5、WY7、WY10、WY12的失稳概率分别为48.29%,52.26%,21.67%,55.04%,均大于文献[16]方法的计算结果,且最大差异高达16.39%,表明在固定危岩体几何尺寸的可靠度分析中,仅考虑结构面等效强度参数变异性的可靠度计算方法较不完备,所得结果往往过于理想,而本文所提方法综合考虑了结构面连通率、分段强度与危岩所受作用力参数的不确定性,计算结果更为准确.结合危岩稳定状态划分标准[18]可知,WY5、WY7、WY12的失稳概率位于30%~60%,属于欠稳定状态,WY10的失稳概率位于5%~30%,为基本稳定状态,该结果与稳定性系数评价标准所得状态相符.因此,本文提出的危岩体可靠度计算方法较为准确合理,具备一定的工程适用性.
| 表 2 危岩体稳定性评价结果 Tab. 2 Stability evaluation results of unstable rock |
分析断续结构面参数及所受作用力参数对危岩失稳概率影响程度的敏感性,在WY7的统计参数区间内,以8因素均值为中心选出各因素的3个水平(表 3),制定8因素3水平的正交表L27(38),同时假定各因素变异系数均为0.1,计算27组试验所得危岩失稳概率如表 3所示.
| 表 3 正交试验因素与水平 Tab. 3 Factors and levels of orthogonal test |
对表 4所得结果进行极差分析,由表 5可知,μη3水平对危岩失稳概率的影响极差34.76%为最大,Rμcr=30.60%次之,其余6项极差值较二者相比均小很多,由大到小分别为μW、μφj、μcj、μφr、μQ、μV,则该8因素对危岩失稳概率影响的敏感性排序为:连通率>未贯通段黏聚力>危岩自重>贯通段内摩擦角>贯通段黏聚力>未贯通段内摩擦角>水平地震力>裂隙水压力,其中连通率为主导因素,未贯通段黏聚力为次主导因素.
| 表 4 正交设计与结果 Tab. 4 Results and design of orthogonal test |
| 表 5 极差分析 Tab. 5 Range analysis results |
如图 2所示,随着μcj、μcr、μφj、μφr的增大,危岩失稳概率均呈下降趋势.其中断续结构面未贯通段黏聚力均值的影响程度最大,危岩失稳概率随之变化区间为66%~35%,证实了其为主导因素,贯通段内摩擦角均值的影响程度次之,贯通段黏聚力与未贯通段内摩擦角均值的影响程度均较小,Pf随之平缓下降.当μη、μQ、μV、μW增大时,危岩失稳概率均有所升高,其中Pf受连通率均值影响的变化区间为33%~68%,为极差分析中最大的变化跨度,表明其对危岩稳定可靠度的评价极其重要,也证实了连通率是影响该危岩稳定可靠度的主导因素.危岩体自重均值的影响程度次之,而水平地震力与裂隙水压力的均值变化对Pf几乎无影响.
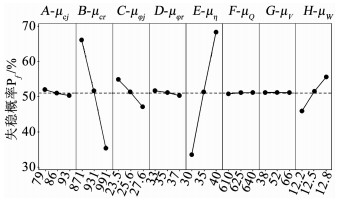
|
图 2 失稳概率正交效应 Fig. 2 Orthogonal test effect of instability probability |
利用Design-Export中的Box-Benhnken方法,构建上节所得主导因素连通率与未贯通段黏聚力的均值及变异系数影响危岩稳定可靠度的试验模型,选取μcr(A)、CVcr(B)、μη(C)、CVη(D)为自变量,以危岩失稳概率为响应值,设计响应面试验,各变量的水平取值见表 6.
| 表 6 响应面试验变量与水平 Tab. 6 Factors and levels of response surface test |
通过已选响应面模型与表 6所示因素水平设计29组试验,各组试验所得危岩体失稳概率见表 7.
| 表 7 响应面试验设计与结果 Tab. 7 Design and results of response surface test |
根据表 7所得结果,变量参数与危岩失稳概率可拟合出的二阶多项式为
Pf=51.97-19.81A+0.33B+22.21C+0.098D+2.3AB+0.87AC+6.73AD-2.42BC+0.15BD-7.39CD+0.007A2-0.55B2-0.32C2-0.57D2.
对上述响应面模型进行方差分析(表 8),由表 8可知模型P<0.000 1,表现为差异极显著;模型与试验间失拟项P=0.053 9>0.05不显著,二者拟合效果较好;确定系数R2=0.992 5>0.8,表明该响应面模型与试验指标具有99.25%的符合度.在一次项中,断续结构面未贯通段黏聚力均值A与连通率均值C的F值分别为782.41,983.79,且二者的P值均小于0.000 1,为影响极显著,验证了连通率为主导因素而未贯通段黏聚力次之.B、D的P值分别为0.650 0,0.891 5,均呈不显著影响,且CVcr对危岩失稳概率的影响程度略大于CVη;在二次项中,连通率与未贯通段黏聚力的均值及变异系数的P值均大于0.05,即响应不显著;在交互项中,响应最为显著的是μη与CVη的交互作用,其概率PCD<0.000 1,F值为36.3,μcr与CVη的交互作用显著性次之,其概率PAD<0.000 1,F值为30.11,除该两项交互作用,其余交互项概率均大于0.05为不显著,且CVcr与CVη的交互概率PBD高达0.907 6,对危岩失稳概率几乎无影响.
| 表 8 响应面模型的方差分析 Tab. 8 Variance analysis of response surface model |
不同变量间交互作用对危岩失稳概率影响的曲面效应关系如图 3所示.由图 3(a)、(b)、(c)可知,在未贯通段黏聚力均值参与的3个交互项中,三维曲面形态及响应指标跨度均有所差别.如图 3(a)所示,μcr与CVcr的交互曲面曲率较小,表明其交互作用对Pf存在一定程度的影响,但响应并不显著,其中当μcr较小时CVcr对Pf的影响是负相关的,随着μcr的增大其负相关趋势逐渐减弱,当μcr增大使得Pf高于50%以后,二者转变为正相关关系.如图 3(b)所示,μcr与μη的交互作用对Pf影响跨度较大,但二者对Pf的影响程度及规律不受彼此大小变化而改变,且该曲面较为平滑,验证了二者对Pf的影响均极显著,而其基本不构成交互作用影响.在图 3(c)中,陡峭的曲面表明μcr与CVη的交互作用对Pf影响极为显著,当μcr较小时,CVη的增大能够使危岩体失稳概率降低13.00%,当μcr较大时,CVη与危岩体可靠度呈正相关关系,Pf随CVη的增大而提升13.92%.在连通率均值μη与CVcr、CVη的两个交互项中(图 3(d)、(e)),CVcr与CVη对应Pf的影响规律与图 3(a)、(c)所示相同,即当μη较小时,Pf随CVcr、CVη增大而分别增大5.97%,14.86%,当μη较大时,Pf随CVcr、CVη增大而分别减小3.70%,14.7%.由图 3(f)可知,当μcr与μη均取中间水平,即Pf趋近于50%时,CVcr与CVη的交互曲面近似为水平面,验证了其交互作用对Pf几乎无影响,且二者单边均无明显改变Pf的大小,表明两因素均值的中间水平使得Pf趋近于转折点.
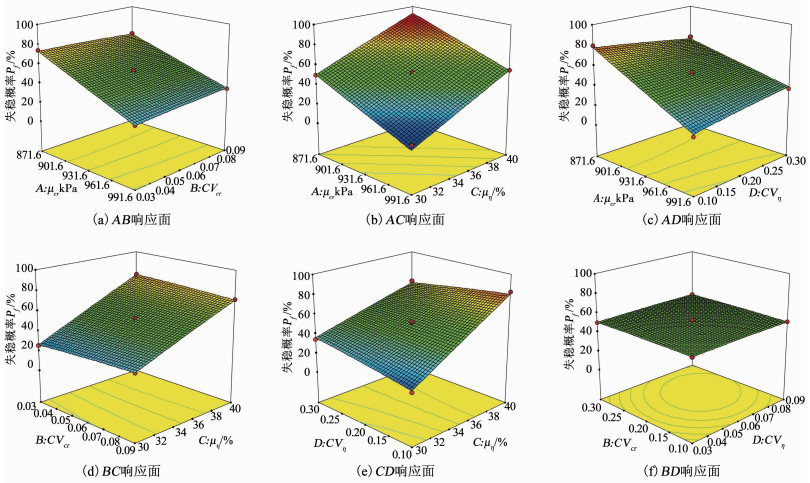
|
图 3 因素变量交互响应面分析 Fig. 3 Response surface analysis of the interaction of factor variables |
由以上分析可知,主导因素连通率及未贯通段黏聚力的均值对Pf的单项影响极为显著,且μη的敏感程度略高于μcr,其中Pf随μcr增大而降低,随μη增大而升高,与5.5.2节中所得结论一致.二者变异系数对Pf的影响规律受均值大小的控制,且WY7中该规律变化的转折点为临界值Pf=50%,当μcr或μη的取值使得Pf高于临界值时,二者的变异系数与Pf呈负相关;当μcr或μη的取值致使Pf低于临界值时,Pf随CV的增大而升高.主导因素均值取值的变化实则表征危岩体所处稳定性状态的改变,即当危岩体处于较不稳定或不稳定状态时,主导因素参数的低变异性会高估危岩体失稳概率,致使对危岩体的可靠度评价过于保守;当危岩体处于发育初期或较稳定状态时,主导因素的低变异性会低估危岩体失稳概率,此时的可靠度评价结果则较不可信.
5 结论1) 在固定危岩体几何尺寸的稳定可靠度分析中,仅考虑结构面等效强度参数变异性的可靠度计算结果多过于安全,而本文所提方法综合考虑了结构面连通率、分段强度与危岩所受作用力参数的不确定性,计算结果更为保守准确.且依据本文方法所得结果划分的危岩体稳定状态与稳定性系数评价标准划分的状态相符,故本文提出的危岩体可靠度计算方法较为准确合理,具备一定的工程适用性.
2) 单面剪切滑动破坏模式下的危岩体断续结构面及所受作用力参数变量的可靠度敏感性排序为:连通率η>未贯通段黏聚力cr>危岩自重W>贯通段内摩擦角φj>贯通段黏聚力cj>未贯通段内摩擦角φr>水平地震力Q>裂隙水压力V,其中η与cr对危岩体失稳概率影响程度较大,为主导因素,其余6因素对危岩体可靠度的影响较小.危岩体失稳概率随连通率与各作用力均值的增大而升高,结构面强度参数的均值与危岩体失稳概率呈负相关关系.
3) 连通率与未贯通段黏聚力的参数变异性对危岩体失稳概率的影响受其均值大小的控制,当参数均值的取值使得危岩体趋于偏失稳状态时,二者的变异系数与失稳概率呈负相关,低变异性参数可能导致可靠度评价结果过于保守;当参数均值的取值使得危岩体趋于偏稳定状态时,失稳概率随变异系数的增大而升高,主导因素参数的低变异性会低估危岩体失稳概率,使得可靠度评价结果较不可信.
4) 本文提出的稳定可靠度分析方法能用于评价断续结构面控制的危岩体可靠性,是一种行之有效的可靠度分析方法.在该类危岩体稳定可靠性评价工作中,要尽可能地详细调查断续结构面相关参数的均值与变异性大小,从而提高危岩体可靠度分析结果的准确性.
| [1] |
冯树荣, 赵海斌, 蒋中明. 节理岩体边坡稳定性分析新方法[J]. 岩土力学, 2009, 30(6): 1639. FENG Shurong, ZHAO Haibin, JIANG Zhongmin. A new method of stability analysis of jointed rock slope[J]. Rock and Soil Mechanics, 2009, 30(6): 1639. DOI:10.16285/j.rsm.2009.06.051 |
| [2] |
王林峰, 陈洪凯, 唐红梅, 等. 地震作用下坠落式危岩稳定性分析[J]. 地下空间与工程学报, 2013, 9(5): 1191. WANG Linfeng, CHEN Hongkai, TANG Hongmei, et al. Stability analysis for falling perilous rock triggered by earthquake[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(5): 1191. |
| [3] |
阙金声, 陈剑平, 石丙飞, 等. 广州科学城岩质边坡稳定性可靠度分析[J]. 岩石力学与工程学报, 2006, 25(增刊2): 3737. QUE Jinsheng, CHEN Jianping, SHI Bingfei, et al. Reliability analysis of rock slope stability in Guangzhou Science City[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl 2): 3737. DOI:10.3321/j.issn:1000-6915.2006.z2.063 |
| [4] |
李典庆, 周创兵. 考虑多失效模式相关的岩质边坡体系可靠度分析[J]. 岩石力学与工程学报, 2009, 28(3): 541. LI Dianqing, ZHOU Chuangbing. System reliability analysis of rock slope considering multiple correlated failure modes[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 541. DOI:10.3321/j.issn:1000-6915.2009.03.013 |
| [5] |
陈鹏, 徐博侯. 基于因素敏感性的边坡稳定可靠度分析[J]. 中国公路学报, 2012, 25(4): 42. CHEN Peng, XU Bohou. Reliability analysis slope stability based on factors sensitivity[J]. China Journal of Highway and Transport, 2012, 25(4): 42. DOI:10.19721/j.cnki.1001-7372.2012.04.007 |
| [6] |
张硕, 路军富, 裴向军, 等. 坠落式危岩体稳定性可靠度判定及参数敏感性分析[J]. 工程地质学报, 2015, 23(3): 429. ZHANG Shuo, LU Junfu, PEI Xiangjun, et al. Analysis of parameter sensitivity and judgement of stability reliability for falling unstable rock[J]. Journal of Engineering Geology, 2015, 23(3): 429. DOI:10.13544/j.cnki.jeg.2015.03.009 |
| [7] |
杨智翔, 裴向军, 袁进科. 基于可靠度理论对滑移式落石的稳定性及敏感性分析[J]. 科学技术与工程, 2017, 17(1): 285. YANG Zhixiang, PEI Xiangjun, YUAN Jinke. The reliability theory to slippage of rockfall stability and sensitivity analysis[J]. Science Technology and Engineering, 2017, 17(1): 285. DOI:10.3969/j.issn.1671-1815.2017.01.052 |
| [8] |
胡波, 张楠, 王思敬, 等. 断续节理岩体模型试验及强度分析研究[J]. 地下空间与工程学报, 2011, 7(4): 657. HU Bo, ZHANG Nan, WANG Sijing, et al. Model test and strength analysis research on intermittent joint rock mass[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(4): 657. |
| [9] |
张浮平, 曹子君, 唐小松, 等. 基于蒙特卡罗模拟的高效边坡可靠度修正方法[J]. 工程力学, 2016, 33(7): 55. ZHANG Fuping, CAO Zijun, TANG Xiaosong, et al. Efficient slope reliability updating method based on Monte Carlo simulation[J]. Engineering Mechanics, 2016, 33(7): 55. DOI:10.6052/j.issn.1000-4750.2015.02.0108 |
| [10] |
蔡静森.斜坡力学参数变异性描述及其稳定性预测[D].武汉: 中国地质大学, 2016 CAI Jingsen. Slope stability prediction based on mechanical parameter variability characterization[D]. Wuhan: China University of Geosciences, 2016 |
| [11] |
方开泰, 马长兴. 正交与均匀试验设计[M]. 北京: 科学技术出版社, 2001. FANG Kaitai, MA Changxing. Orthogonal and uniform experimental design[M]. Beijing: Science and Technology Press, 2001. |
| [12] |
MASON R L, GUNST R F, HESS J L. Statistical design and experiments with applications to engineering and science[M]. New York: John Wiley and Sons Publication, 2003.
|
| [13] |
FREIRE L, CARMEZIM M J, FERREIRA M G S, et al. The passive behaviour of aisi 316 in alkaline media and the effect of pH: A combined electrochemical and analytical study[J]. Electrochimica Acta, 2010, 55(21): 6174. DOI:10.1016/j.electacta.2009.10.026 |
| [14] |
RANJBARI E, HADJMOHAMMADI M R. Optimization of magnetic stirring assisted dispersive liquid-liquid microextraction of rhodamine b and rhodamine 6g by response surface methodology: Application in water samples, soft drink, and cosmetic products[J]. Talanta, 2015, 139: 216. DOI:10.1016/j.talanta.2015.02.051 |
| [15] |
李漪, 晏鄂川, 胡显明, 等. 南门湾滑移式危岩体风险评价研究[J]. 长江科学院院报, 2011, 28(5): 14. LI Yi, YAN Echuan, HU Xianming, et al. Risk assessment for Nanmenwan sliding dangerous rock masses[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(5): 14. DOI:10.3969/j.issn.1001-5485.2011.05.004 |
| [16] |
王林峰, 陈洪凯, 唐红梅. 危岩稳定可靠度计算方法研究[J]. 人民长江, 2012, 43(23): 14. WANG Linfeng, CHEN Hongkai, TANG Hongmei. Study on the calculation method of stable reliability of dangerous rock[J]. Yangtz River, 2012, 43(23): 14. DOI:10.16232/j.cnki.1001-4179.2012.23.003 |
| [17] |
重庆市质量监督局. DB50/143—2003地质灾害防治工程勘察规范[S]. 2003
|
| [18] |
张倬元, 王士天, 王兰生. 工程地质分析原理[M]. 北京: 地质出版社, 2005. ZHANG Zhuoyuan, WANG Shitian, WANG Lansheng. Principle of engineering geology analysis[M]. Beijing: Geological Publishing House, 2005. |
 2019, Vol. 51
2019, Vol. 51


