岩石的形成过程以及其后的地质作用会使其内部存在夹层、裂隙等各种缺陷,也使各种岩石甚至是同一种岩石的成分和结构特征各有差异,从而使岩石在受力作用时变形呈现明显的非线性特征.应力与应变关系是开展多孔及裂隙岩体变形与应力分析的基础,传统胡克定律已被广泛应用于岩体的线弹性变形分析.然而,已有很多研究表明,即便是传统的弹性变形阶段,很多情况下岩体的应力-应变关系也表现出强烈的非线性行为[1-4].
席道瑛等[5-6]引入一种滞后非线性弹性材料的宏观模型——Preisach-Mayergoyz模型(PM模型),该模型通过大量分散的滞后细观单元的应力对加载与卸载的响应不是原路可逆的特性,导致在循环荷载作用下多孔饱和岩石具有滞后和离散记忆的特征,以此来描述岩石的滞后和离散记忆,通过岩石细观单元的应力来描述岩石宏观的滞后性.
孔志鹏等[11]提出一种岩石材料非线性三参数强度准则,待定系数A、B、C是关于岩石材料极限应力比值的函数,可通过简单的试验确定.A Lionco等[7-9]将模量表征为应力或者围压某一形式的函数,利用唯像的经验公式实现对岩体弹性变形阶段的非线性行为的捕捉.理论上,对于岩石介质的非线性弹性行为,一致认可的是岩石本身严重的不均匀性,如普遍存在的、尺度在微米量级的裂纹、结合、接缝等微观结构,但又没有定量化的线性规律来表征,因此,包雪阳等[10]从微观结构的概率分布入手建立统计模型,但仍很难将这种微观尺度的假设与宏观尺度的力学响应建立起具体的表征关系.本文针对深部近千米岩石进行岩石力学试验后,分析其物理力学参数弹性模量及泊松比的非线性变化特性,应用双曲线函数拟合出岩石的体积模量和剪切模量与岩石三向受力状态下平均应力函数的参量,且参数的物理意义明确.并将其应用到CSIRO地应力测量方法中高围压率定公式计算中.
1 深部花岗岩单、三轴压缩抗压强度试验MTS815岩石力学测试系统应变监测采用MTS夹式轴向应变伸长计进行轴向应变测量.采用该技术可有效消除传统测试方法中的误差,即通过测量加载框架位移用以计算试件应变过程中所包含的框架-框架和框架-试件接合处的变形误差.三轴压缩试验中采用环向应变控制的方式加载,径向伸长计通过刚性链条链接,如图 1所示.

|
图 1 轴向和环向引伸计 Fig. 1 Axial and circumferential extensimeter |
试验花岗岩试件取自山东莱州三山岛金矿-795水平,埋深近千米.应用钻机在巷道边帮套筒取芯,然后进行制样工作,主要包括岩样切割、岩样钻取、岩样打磨等过程,使用车床精确加工,加工成标准圆柱体试件,精度满足国际岩石力学学会(ISRM)规定的室内岩石力学试件的精度要求.见图 2,3.

|
图 2 钻机套筒取芯 Fig. 2 Core removal using drill sleeve |

|
图 3 花岗岩岩石试件 Fig. 3 Granite rock specimen |
为消除岩石试件两端面不平整引起试验数据误差,保证岩石力学室内试验数据的可靠性,试样端面精度必须满足要求,因此,应用0.002级高精度大理石比测台配合千分尺进行试件端面平整度精度测量,不满足精度要求的试件不能进行试验.
针对近千米花岗岩进行了单轴、三轴岩石压缩试验,获得单轴及围压10,30,50 MPa下岩石应力应变曲线.
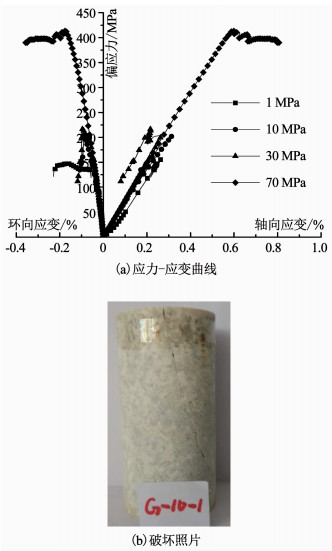
各围压下三山岛金矿花岗岩应力-应变曲线见图 4.
|
图 4 三山岛金矿花岗岩应力-应变曲线及破坏照片 Fig. 4 Stress-strain curve and damage photo of Sanshandao Gold Deposit granite under different confining pressures |
由图 4可知,围压10和30 MPa轴向应变过抗压峰值后,轴向应变数据出现异常,是岩样和热缩管脱离造成,热缩管与岩样脱离只是导致应变测量不准确,力是由顶部压力传感器获得,因此,不影响试件抗压强度.围压越大花岗岩三轴抗压强度越大,但不与围压成线性增加关系,且由于花岗岩节理裂隙较多个别试验数据波动较大,低围压时应力应变曲线压密阶段很明显,但随着围压增大压密阶段几乎消失,弹性模量E随围压增加而增大,但每个岩样各向异性比较突出,弹性模量随围压增大的规律性不强.
2 三山岛金矿深部花岗岩非线弹性变形规律试验山东黄金集团有限公司三山岛金矿是山东黄金集团主体矿山之一,下设三山岛金矿直属矿区和新立矿区.其中直属矿区目前已进入深部开采,开采深度将逼近并超过1 000 m.随着开采深度的增加,地应力增大,地质条件恶化,涌水量加大,地温升高,开采工作面作业环境恶化.由此导致地压显现加剧,巷道围岩变形、塌方、冒顶、片帮等事故隐患日渐增多.为了解决上述深部开采中出现的一系列问题,必须对直属矿区深部目前已开拓部分进行系统的三维地应力场测量及岩石力学特性进行相应的研究.
2.1 试验加载方案由于三山岛花岗岩内含较大结晶颗粒,且节理裂隙较为发育,不同岩样之间差异较大,各向异性突出,不同岩样各个围压下试验数据计算的弹性模量和泊松比规律性不强,因此,设计一种单个岩样在几个不同围压下弹性阶段加载试验,此试验获得的应力-应变数据所计算的物理力学参数,可以大大消除因不同岩样之间各向异性引起的数据误差,为构建岩石非线弹性理论提供可靠力学试验数据.
常规三轴压缩抗压强度试验,获得低围压到高围压三轴抗压强度,拟合出霍克布朗强度准则,根据公式拟合参数计算出三山岛花岗岩10,30,50 MPa围压下抗压强度,单岩样阶梯加载时轴向最大压力均小于其抗压强度的50%,具体试验加载值与计算值见表 1.
| 表 1 单岩样多围压阶梯加载方案 Tab. 1 Single rock sample multi-confining pressure step loading test plan |
围压10,30,50 MPa轴向加载最大压力占各自抗压强度的23.6%,27.7%,36.5%,位于弹性变形加载阶段.
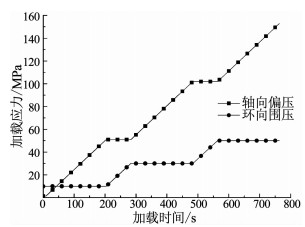
由图 5加载路径可以看出,偏压及围压成阶梯状加载,故称为单岩样多围压阶梯加载试验.
|
图 5 单岩样多围压阶梯加载加载路径 Fig. 5 Load path for single rock sample multi-confining pressure step loading test |
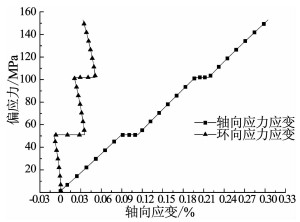
由单岩样多围压阶梯加载全应力应变图(图 6)可知,分别在围压10,30,50 MPa下进行轴向加载,当围压10 MPa时,采用轴向控制,按力0.5 kN/s速率加载,加载到100 kN,此阶段轴向为压缩变形,环向为膨胀变形;当轴向偏压加载到100 kN立刻切换控制方式,变为环向应力控制,围压由10 MPa按0.025 MPa/s速率加载到30 MPa,此阶段轴向和环向均为压缩变形;以此类推加载到围压50 MPa,轴向压力150 kN.对轴向每5 MPa应力范围进行应力-应变数据提取,计算各个范围内的弹性模量E和泊松比ν, 结果见表 2.
|
图 6 单岩样多围压阶梯加载应力-应变曲线 Fig. 6 Stress-strain data for single rock sample multi-confining pressure step loading test |
| 表 2 单岩样多围压岩石物理力学参数 Tab. 2 Physical and mechanical parameters for single rock sample under multiple-confining pressure |
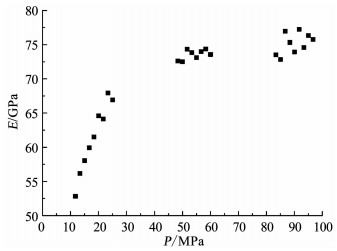
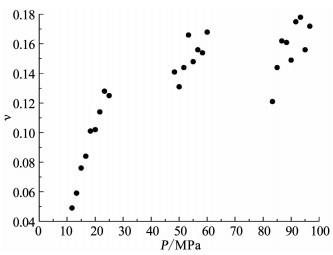
由弹性模量与平均应力图(图 7)和泊松比与平均应力图(图 8)可知,开始阶段平均应力增加很小岩样物理力学参数弹性模量E和泊松比ν增加很快即其变化速率很大且近似线性增加,到后期非线性变化特征越发明显,其变化速率也不断减小.单独研究弹性模量和泊松比与平均应力的关系不科学.因此,引入体积模量K和剪切模量G,且与弹性模量和泊松比关系式为
|
图 7 弹性模量与平均应力 Fig. 7 Elastic modulus vs. mean stress |
|
图 8 泊松比与平均应力 Fig. 8 Poisson's ratio vs the mean stress |
| $ K = \frac{E}{{3(1 - \nu )}}, G = \frac{E}{{2(1 + \nu )}}. $ | (1) |
平均应力P表示岩样的三维受力状态,其计算式为(σ1+σ2+σ3)/3,三轴压缩岩石试验中σ2=σ3,σ1为偏压,则平均应力可以表示为(σ1+3σ3)/3.计算每5个MPa轴向应力范围内的体积模量K和剪切模量G,结果见表 3.
| 表 3 各个围压下变形模量 Tab. 3 Deformation modulus under different confining pressures |
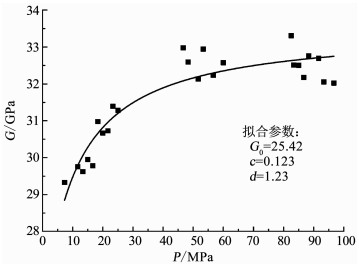
图 9,10中体积模量K和剪切模量G与平均应力P的关系是非线性, 应用双曲线函数模型表示深部岩石非线性变形特征,且双曲线函数模型拟合公式为

|
图 9 体积模量与平均应力数据拟合 Fig. 9 Bulk modulus and mean stress data fitting |
|
图 10 剪切模量与平均应力数据拟合 Fig. 10 Shear modulus and mean stress data fitting |
| $ K = {K_0} + \frac{P}{{b + a \times P}}, $ | (2) |
| $ G = {G_0} + \frac{P}{{d + c \times P}}. $ | (3) |
式中:P为平均应力,K0,G0为初始体积模量和初始剪切模量,即当P为0时,K和G的取值.参数a,b,c,d的物理意义如下:
| $ \frac{1}{b} = {\left. {\frac{{{\rm{d}}K}}{{{\rm{d}}P}}} \right|_{P = 0}}, $ | (4) |
| $ \frac{1}{a} = {\left. K \right|_{P = \infty }} - {K_0} = \Delta {K_{{\rm{ult}}}}, $ | (5) |
| $ \frac{1}{d} = {\left. {\frac{{{\rm{d}}G}}{{{\rm{d}}P}}} \right|_{P = 0}}, $ | (6) |
| $ \frac{1}{c} = {\left. G \right|_{P = \infty }} - {G_0} = \Delta {G_{{\rm{ult}}}}. $ | (7) |
论文第2部分是获得岩石试件三轴抗压强度,从而大致计算出各个围压下的弹性段,为第3部分单岩样多围压阶梯加载试验提供试验方案加载数据,分析试验数据后提出了一种岩石非线性本构关系.但在地应力计算过程中需要用到空心包体双轴加载试验,确定岩石的物理参数弹性模量和泊松比.此部分是验证岩石非线性本构关系,依然适用于空心包体双轴加载试验.
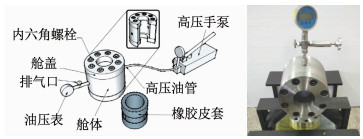
3.1 试验装置的研制目前,国内外使用的围压率定仪器是澳大利亚公司es & s生产,其理论加压值为40 MPa,但实验室可测最大围压为16 MPa,不能满足深部岩体空心包体地应力测量中双轴加载试验的高围压要求,因此,本课题组收集大量的资料后,根据自密封原理研制出高围压率定仪器试验系统,如图 11所示,试验测试加载最大值为70 MPa,且具有保压性能稳定、加卸压方式操作简单等优点.
|
图 11 双轴加压装置各个组成部分及实物 Fig. 11 Components and photo of biaxial pressure device |
自2013年开始,课题组对空心包体应变计数字化技术进行研究[12],在保证采集精度和稳定性前提下开发具有瞬时采集、断电续采、漂移自补偿等功能的采集板路,并根据蔡美峰院士提出的完全温度补偿理念,设计研发了双温度补偿电路.经过不断地研发和改进,目前本地数字化探头采用的是第5代电路产品,如图 12.电路采用微处理器芯片,5 V蓄电池供电,以稳压芯片代替传统的稳压模块,多路模拟开关分别控制各通道开合;瞬时采集技术的引入,避免了采集系统发热和电流变化引起采集误差.采集电路留有16个输入通道.采用恒温试验箱进行电路板温度稳定性试验,结果显示采集仪48 h温漂最大为2με.采用标准应变发生器进行采集电路精度测试,结果显示采集精度为0.01微应变[12].采用标准应变发生器进行断电续采功能测试,断电2 min后续采(温度无变化),采集数据断电前后误差小于1‰.

|
图 12 数字化型应变仪采集系统 Fig. 12 Micro acquisition card |
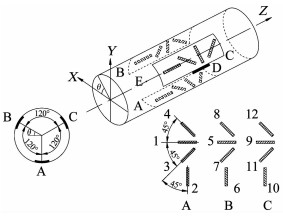
高围压率定试验又称高压双轴加载试验,所用大尺寸岩芯取自三山岛金矿埋藏近千米的花岗岩,三组应变片成120°胶粘于小孔内壁,应变花顺时针顺序为A-B-C.以A组应变片为例,1片为环向应变片记为A90;2片为轴向应变片记为A0;3和4片分别与钻孔轴线成±45°,记为A45,A135.具体位置见图 13,围压按梯度5 MPa进行加载,然后手动采集应变数值,最终所取应变数据浮动不超过5个微应变,试验过程见图 14.
|
图 13 应变片粘贴位置示意 Fig. 13 Schematic diagram for strain gauge paste position |

|
图 14 岩石双轴压缩试验过程照片 Fig. 14 Rock biaxial pressurization test process |
内含无线传输改进型空心包体应变计的解除岩芯,应用自主研制的高压双轴加载试验仪器进行双轴加载试验后,测得应变花的εθ和εa对应值,计算测点岩石弹性模量Ep和泊松比νp,即
| $ {E_{\rm{p}}} = \frac{{\Delta {\sigma _r}}}{{\Delta {\varepsilon _\theta }}}\frac{{2{R^2}}}{{{R^2} - {r^2}}}, {\nu _{\rm{p}}} = - \frac{{\Delta {\varepsilon _a}}}{{\Delta {\varepsilon _\theta }}}. $ | (8) |
式中:εθ和εa分别为垂直小孔的应变和与小孔方向一致的应变,σr为围压值,R为岩芯外径,r为小孔半径.
且体积模量K和剪切模量G与弹性模量E和泊松比ν关系式为
| $ K = \frac{E}{{3(1 - 2\nu )}}. $ | (9) |
| $ G = \frac{E}{{2(1 + \nu )}}. $ | (10) |
将式(9)带入式(10)和(11)得
| $ K = \frac{{\frac{{\Delta {\sigma _r}}}{{\Delta {\varepsilon _\theta }}}\frac{{2{R^2}}}{{{R^2} - {r^2}}}}}{{3\left( {1 + 2\frac{{\Delta {\varepsilon _a}}}{{\Delta {\varepsilon _\theta }}}} \right)}}, $ | (11) |
| $ G = \frac{{\frac{{\Delta {\sigma _r}}}{{\Delta {\varepsilon _\theta }}}\frac{{2{R^2}}}{{{R^2} - {r^2}}}}}{{2\left( {1 - \frac{{\Delta {\varepsilon _a}}}{{\Delta {\varepsilon _\theta }}}} \right)}}. $ | (12) |
平均应力与围压关系为
| $ P = \frac{{2{\sigma _r}}}{3}. $ | (13) |
式(11)和(12)化简得
| $ K = \frac{{\Delta P}}{{\Delta \left( {{\varepsilon _\theta } + 2{\varepsilon _a}} \right)}} \cdot \frac{{{R^2}}}{{{R^2} - {r^2}}}, $ | (14) |
| $ G = \frac{{3\Delta P}}{{2\Delta \left( {{\varepsilon _\theta } - {\varepsilon _a}} \right)}} \cdot \frac{{{R^2}}}{{{R^2} - {r^2}}}. $ | (15) |
将式(2)和(3)带入(11)和(12)化简得
| $ \Delta \left( {{\varepsilon _\theta } + 2{\varepsilon _a}} \right) = \frac{{(a + b \cdot P)\Delta P}}{{a \cdot {K_0} + \left( {b \cdot {K_0} + 1} \right)P}} \cdot \frac{{{R^2}}}{{{R^2} - {r^2}}}, $ | (16) |
| $ \Delta \left( {{\varepsilon _\theta } - {\varepsilon _a}} \right) = \frac{{(c + d \cdot P)\Delta P}}{{c \cdot {K_0} + \left( {d \cdot {K_0} + 1} \right)P}} \cdot \frac{{3{R^2}}}{{2\left( {{R^2} - {r^2}} \right)}}. $ | (17) |
将式(16)和(17)两边同时积分,且公式包含应变为0和平均应力为0的情况,即
| $ \begin{array}{l} \left( {{\varepsilon _\theta } + 2{\varepsilon _a}} \right) = \frac{{{R^2}}}{{{R^2} - {r^2}}} \cdot \left[ {\frac{{b \cdot P}}{{b \cdot {K_0} + 1}} + \frac{a}{{{{\left( {b \cdot {K_0} + 1} \right)}^2}}}} \right. \cdot \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ln \left[ {\frac{{a \cdot {K_0} + \left( {b \cdot {K_0} + 1} \right)P}}{{a \cdot {K_0}}}} \right]} \right]. \end{array} $ | (18) |
| $ \begin{array}{l} \left( {{\varepsilon _\theta } - {\varepsilon _a}} \right) = \frac{{3{R^2}}}{{2\left( {{R^2} - {r^2}} \right)}} \cdot \left[ {\frac{{d \cdot P}}{{\left( {d \cdot {G_0} + 1} \right)}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{c}{{{{\left( {d \cdot {G_0} + 1} \right)}^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\ln \left[ {\frac{{c \cdot {G_0} + \left( {d \cdot {G_0} + 1} \right)P}}{{c \cdot {G_0}}}} \right]} \right]. \end{array} $ | (19) |
将高围压加载试验数据应变和平均应力计算处理后得表 4,利用式(18)和(19)拟合数据结果见图 15.
| 表 4 应变与平均应力数据 Tab. 4 Strain and mean stress data |
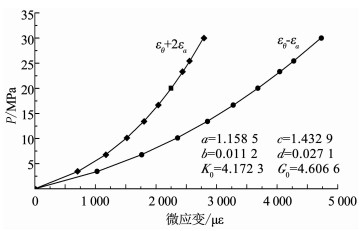
|
图 15 平均应力与应变及非线弹性本构关系参数拟合 Fig. 15 Nonlinear fitting of the constitutive relation between the bulk modulus and shear modulus vs. mean stress |
图 15平均应力与应变拟合度相当高,数据点和曲线之间应用最小二乘法寻找最小残余误差平方和为4.32和3.64 MPa2.因此,所提出的非线性本构关系可以用来描述现场岩石的非线性行为.
4 结论1) 单岩样多围压阶梯加载试验,获取的数据更具有规律性,计算了在不同平均应力下弹性模量与泊松比数值,随着平均应力增加弹性模量和泊松比都成非线性增加,开始阶段增长率较大,后期增长率逐渐变小.
2) 分析处理单岩样多围压三轴加载试验数据,获得每5 MPa偏压范围内平均应力与体积模量和剪切模量数据,基于双曲线函数模型,提出了一种非线性本构,且本构关系中三参数物理意义明确.
3) 将提出的非线弹性本构关系,引入空心包体解除法地应力测量中的围压率定公式,此公式考虑岩石非线弹性变形规律,为深部岩体CSIRO地应力测量法提供了一种非线性计算方法.
| [1] |
BROWN E T, BRAY J W, SANTARELLI F J. Influence of stress-dependent elastic moduli on stresses and strains around axisymmetric boreholes[J]. Rock Mechanics and Rock Engineering, 1989, 22(3): 189. DOI:10.1016/0148-9062(90)95304-j |
| [2] |
NAWROCKI P A, DUSSEAUIJ M B, BRATLI R K, et al. Assessment of some semi-analytical models for nonlinear modelling of borehole stresses[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 35(4): 512. DOI:10.1016/s0148-9062(98)00050-3 |
| [3] |
LIONCO A, ASSIS A. Behavior of deep shafts in rock considering nonlinear elastic models[J]. Tunnelling and Underground Space Technology, 2000, 15(4): 445. DOI:10.1016/s0886-7798(01)00013-x |
| [4] |
CORKUM A G, MARTIN C D. Modeling a mine-by test at the Mont Terri rock laboratory, Switzerland[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 846. DOI:10.1016/j.ijrmms.2006.12.003 |
| [5] |
席道瑛, 王鑫, 陈运平. 描写岩石非线性弹性滞后和记忆的宏观模型[J]. 岩石力学与工程学报, 2005, 24(20): 2212. XI Daoying, WANG Xin, CHEN Yunping. Macroscopic model of hysteresis and memory for the description of rock nonlinear elastic[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(20): 2212. |
| [6] |
席道瑛, 陈运平, 陶月赞. 岩石的非线性弹性滞后特征[J]. 岩石力学与工程学报, 2006, 25(6): 1083. XI Daoying, CHEN Yunping, TAO Yuezan. Nonlinear elastic hysteric characteristics of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1083. |
| [7] |
WENG M C, JENG F S, HSIEH Y M, et al. A simple model for stress-induced anisotropic softening of weak sandstones[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 155. DOI:10.1016/j.ijrmms.2007.04.004 |
| [8] |
JAEGER J C, COOK N G W, ZIEMMERMAN R W. Fundamentals of rock mechanics[M]. Oxford: Blackwell, 2007: 75.
|
| [9] |
LIU H H, RUTQVIST J, BERRYMAN J C. On the relationship between stress and elastic strain for porous and fractured rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 289. DOI:10.1016/j.ijrmms.2008.04.005 |
| [10] |
包雪阳, 施行觉. 岩石非线性弹性的实验研究及其P-M模型的理论解释[J]. 岩石力学与工程学报, 2004, 23(20): 3397. BAO Xueyang, SHI Xingjue. Experiment research and interpretation on nonlinear elasticity of rock using P-M model[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3397. DOI:10.3321/j.issn:1000-6915.2004.20.002 |
| [11] |
孔志鹏, 孙海霞, 陈四利. 岩石材料的一种非线性三参数强度准则及应用[J]. 岩土力学学报, 2017, 38(12): 3524. KONG Zhipeng, SUN Haixia, CHEN Sili. A nonlinear tri-parameter strength criterion for rock materials and its application[J]. Rock and Soil Mechanics, 2017, 38(12): 3524. |
| [12] |
李振.改进型空心包体本地数字化技术研发及数据误差分析[D].北京: 北京科技大学, 2015 LI Zhen. Research on the local digital technology and data error analysis with method of improved hollow inclusion technique[D]. Beijing: University of Science and Technology Beijing, 2015 |
 2019, Vol. 51
2019, Vol. 51


