在加筋土技术中,土工格栅常被作为筋材来提高土体的剪切力学性能,由于筋土作用的复杂性,荷载在筋土界面间的传递机理还未被充分揭示[1-2].传统筋土界面摩擦特性试验(如格栅拉拔试验)仅能测试土工格栅夹持端的拉拔阻力,而不能直接观测筋土界面间力的传递过程,并且土工格栅的传统测量方法也无法监测到筋土界面连续的位移场,从而无法反映格栅整体的位移状态[3].为了克服这些限制,Sugimoto等[4]在拉拔试验中利用X-射线记录嵌入土工格栅附近土体中铅块的位移,借此得到了格栅的位移分布与拉拔力关系的表达式. Ezzein等[5]采用新型的可视化拉拔设备,运用数字图像法(DIC)基本确定了双向格栅位移影响的范围.随着土工试验中可视化技术推广和应用,筋土界面中土体位移场已经得以准确、有效地捕捉,但是界面间荷载传递机理还有待研究[6].
为了弥补物理试验的不足,国内外学者采用数值分析方法对筋土界面的应力应变关系和位移模式进行了系列研究.闫澍旺等[7]利用有限元分析方法建立了平面应力问题分析模型很好地反映土工格栅在拉拔状态下的变形特性.Siriwardane等[8]使用三维有限元程序评估柔性路面加筋的工作性能,结果表明,筋土界面性质对加筋构筑物的抗拔承载力产生了显著影响.Hussein等[9]分析不同界面参数对拉拔阻力的影响,得到格栅横肋的被动承载力和格栅表面摩擦力对拉拔阻力的贡献值.这些基于有限元的模拟方法无法从细观尺度描述筋土界面区域土颗粒的位移和旋转状态.
为了研究筋土界面细观特性,周健等[10]采用数码可视化跟踪技术,研究筋土界面相互作用的机制,指出活跃的砂土颗粒主要集中在筋土上界面.陈建峰等[11]通过DEM方法开发异形砂土颗粒研究筋土界面特性,发现低压工况下,剪切界面厚度与法向压力呈负相关的线性关系.Wang等[12]通过二维离散元程序建立土工格栅非线性应力应变模型,模拟筋材在砂土中的复合拉伸试验,基本得到了筋土界面间力的传导机理.苗晨曦等[13]借助三维离散元程序研究了界面速度场与筋土间的相互关系,并提出了基于拉拔试验结果的格栅加筋性能评价方法.基于细观尺度的筋土界面力学特性研究成果较多,但通过离散元方法,在考虑土工格栅的非线性应力-应变关系基础上,研究筋土界面处剪切带的形成和演化的成果相对较少,且缺少筋土界面处土体的运动规律与剪切带变化之间关系的研究.
本文基于Ferreira的土工格栅与玻璃砂界面测试结果[14],采用离散元程序PFC2D开展土工格栅加筋玻璃砂颗粒的拉拔模拟试验.以格栅非线性本构关系为基础,研究了拉拔过程中剪切带的形成机制和演化机理,分析了剪切带内外颗粒的运动规律,确定了剪切带中细观组构参量和宏观应力之间的相互联系.
1 颗粒流模拟 1.1 数值模拟和标定采用PFC2D建立数值模型,为了匹配玻璃砂颗粒和土工格栅的物理性质,分别采用数值双轴压缩试验和数值拉伸试验进行标定.
1.2 双轴压缩试验根据文献[14]物理拉拔试验中的玻璃砂颗粒,该玻璃砂颗粒近似圆形.数值双轴试验中采用圆盘颗粒模拟玻璃砂颗粒,颗粒间采用无黏性的线性接触模型模拟,试样宽度76 mm、高度152 mm,与实际三轴试样尺寸相同.根据文献[13]的方法确定二维模型试样孔隙率为0.16,玻璃砂颗粒粒径较大,本文对玻璃砂按原粒径模拟.
图 1为数值试样与文献[14]物理试验中玻璃砂颗粒的级配图.为了减小整个数值模型试样的初始应力,根据孔隙率和颗粒级配采用分层压实法(IMCM)[15]分为4层压实试样.当试样生成后,为了使模拟更加接近真实玻璃砂颗粒的性质,在随后的模拟中将初始颗粒的摩擦系数0调整为3,弥补了圆盘颗粒无棱角的劣势.

|
图 1 玻璃砂颗粒级配 Fig. 1 Particle size distributions in laboratory tests and DEM simulations |
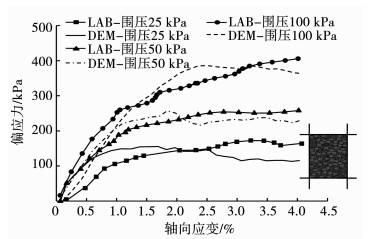
数值双轴试验按照物理试验的过程分别在25,50,100 kPa的围压下进行模拟.通过调整玻璃砂颗粒的细观参数来满足宏观强度的要求,最后确定模型中材料的细观参数,见表 1.玻璃砂颗粒在不同围压下物理试验与数值双轴试验的偏应力-轴向应变对比,如图 2所示(图中LAB为文献[14]室内三轴试验结果).可以看出,数值模型的细观参数能很好反映玻璃砂颗粒的物理力学性质.
| 表 1 玻璃砂颗粒的细观参数 Tab. 1 Meso-mechanical parameters of sand particles |
|
图 2 玻璃砂颗粒物理试验与数值试验对比 Fig. 2 Comparison of curves between DEM simulations and laboratory tests |
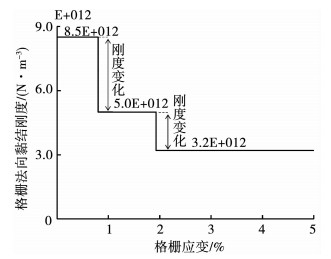
文献[14]中物理拉拔试验所采用的格栅为Tensar BX1100聚丙烯双向土工格栅.在数值拉伸试验中采用2种不同粒径且没有重叠的颗粒模拟土工格栅,以表现土工格栅对砂颗粒的嵌锁作用.在PFC2D中颗粒间的平行黏结能承受颗粒间的力和力矩,本模拟中采用平行黏结接触模型模拟土工格栅的拉伸性质强度高的特点.为了更好地重现格栅物理拉伸试验中所表现出的非线性应力-应变关系,本数值模拟根据文献[12]采用分段函数描述其在拉伸条件下的应力-应变关系.格栅刚度与应变的关系如图 3所示.土工格栅应力-应变关系分段函数的表达式为.
| $ F = \left\{ \begin{array} { l } { k _ { 1 } \cdot \varepsilon , 0 < \varepsilon < 0.8 }, \\ { k _ { 1 } \cdot 0.8 + k _ { 2 } \cdot ( \varepsilon - 0.8 ) , 0.8 < \varepsilon < 1.93 }, \\ { k _ { 1 } \cdot 0.8 + k _ { 2 } \cdot ( 1.93 - 0.8 ) + k _ { 3 } \cdot ( \varepsilon - 1.93 ) }, \\ { \varepsilon > 1.93 } .\end{array} \right. $ | (1) |
|
图 3 土工格栅的刚度与应变关系 Fig. 3 Stiffness-strain relation of the geogrid |
式中:F为格栅夹持端的拉力;ε为格栅的平均应变;0,0.8,1.93为临界应变值;k1,k2,k3为分段函数的斜率(在临界应变值时通过调整格栅的法向黏结刚度依次获取k1,k2,k3),k1,k2,k3的量纲同拉力F.
拉伸结果显示数值拉伸试验的曲线与物理试验基本一致,如图 4所示.拉拔模型中格栅细观参数见表 2.

|
图 4 土工格栅的应力-应变关系对比 Fig. 4 Comparison between stress-strain relation of the geogrid |
| 表 2 土工格栅的细观参数 Tab. 2 Meso-mechanical parameters of the geogrid |
物理拉拔试验模型尺寸为250 mm×300 mm×150 mm(长×宽×高),数值试验中建立与物理试验中相同尺寸的平面拉拔模型,格栅构件在拉拔盒中的长度为233 mm.
在数值拉拔试验中玻璃砂颗粒采用线性接触模型,格栅单元采用平行黏结接触模型,将上述标定的细观参数分别赋予玻璃砂颗粒和格栅颗粒.拉拔试验模型中颗粒的具体生成方法为:1)采取分层压实法(IMCM)[15],生成拉拔盒下盒第1和第2层玻璃砂颗粒层,并通过循环消除每层的不平衡力;2)在第2层玻璃砂颗粒的顶端生成土工格栅颗粒层;3)采用同样程序生成第3和第4层玻璃砂颗粒;4)通过伺服机制施加21 kPa法向应力(参照文献[14],法向应力取21 kPa)到拉拔盒上,完成试样的初始状态,如图 5所示.5)拉拔前将模型内所有颗粒的位移和速率清零,并将摩擦系数附加给颗粒;6)在拉拔过程中保持法向应力不变,将土工格栅最左边的颗粒设置恒定拉拔速率1 mm/min,将土工格栅拔出拉拔盒15 mm,并记录试验过程中的各种变量.试样的初始状态如图 5所示.

|
图 5 试样的初始状态 Fig. 5 Initial state of the pull-out model specimen |
根据文献[14]知,当格栅位移大于5 mm时,玻璃砂颗粒的剪胀现象显著,由于拉拔试验仪器的边界限制了砂颗粒的剪胀,增加了玻璃砂颗粒和拉拔盒拉拔端边界间的摩阻力,因此,拉拔阻力会出现增长的趋势.基于上述现象,由于格栅位移大于5 mm时,拉拔阻力受试验仪器的影响较大,故分析格栅位移小于5 mm的现象.数值试验与室内物理试验的拉拔阻力与位移的对比曲线,如图 6所示.可以看出,在物理试验中当土工格栅位移小于3 mm时,拉拔阻力随着格栅位移的增加而增加;当格栅位移大于3 mm时,拉拔阻力曲线趋于稳定.当格栅位移小于5 mm时,数值试验与物理试验曲线呈现出大体相同的规律,且格栅位移小于3 mm时,两种试验方法得到的曲线基本重合.这说明在格栅位移较小时,离散元数值试验能较好地重现室内物理试验的受力结果.

|
图 6 拉拔阻力与格栅位移的对比曲线(修改自文献[14]) Fig. 6 Curves of geogrid pull-out load-displacement (adopted from Ref. [14]) |
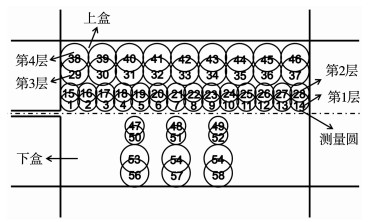
PFC2D程序可以布置测量圆获取材料内部的细观参数,由于拉拔试验模型界面条件基本相同[10],拉拔盒中测量圆的具体布置如图 7所示,下盒中布置较少的测量圆作对比分析.为了捕捉玻璃砂颗粒与土工格栅界面的性状,以及精确地获取大主应力方向的变化规律,图 7中将测量圆重叠设置,距离土工格栅较近的2排采用直径较小的测量圆,距离土工格栅较远的2排采用较大直径的测量圆.直径较小的测量圆每排14个,直径为19.12 mm,直径较大的测量圆每排9个,直径为28.68 mm.
|
图 7 试样的测量圆布置 Fig. 7 Layout of measurement circles |
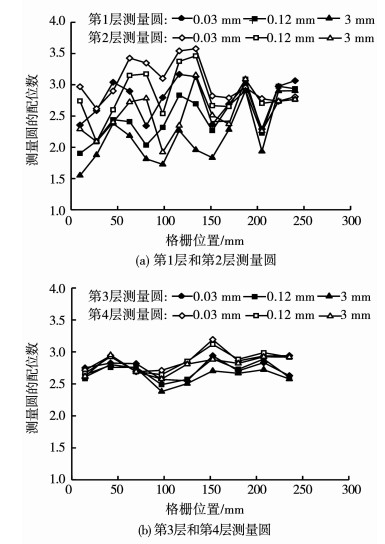
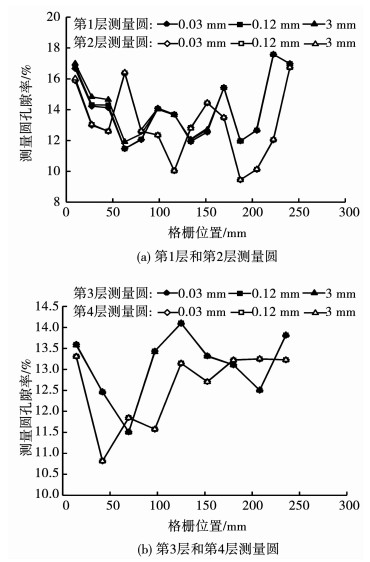
图 8,9中曲线分别表示格栅位移为0.03,0.12,3 mm时,沿格栅纵向布置的不同层高测量圆内配位数和孔隙率的变化.由图 8(a)可以看出,随着格栅位移的增加,沿着格栅纵向分布的第1层和第2层测量圆内配位数呈明显降低的趋势,且随离格栅拉拔端距离的增加,同一层测量圆内配位数的变化逐渐变小.由图 8(b)可以看出,当格栅位移为3 mm时,第3层和第4层测量圆内的配位数小幅波动.随着格栅位移增加,沿着格栅纵向分布的第1层和第2层测量圆内孔隙率呈现明显增加的趋势,如图 9(a)所示.但第3层和第4层测量圆内孔隙率并不随着格栅位移增加而增加,与初始孔隙率相比,基本不变,如图 9(b)所示.
|
图 8 配位数沿土工格栅纵向分布 Fig. 8 Coordination distributions along the geogrid |
|
图 9 孔隙率沿土工格栅纵向分布 Fig. 9 Distribution of porosity along the geogrid |
由图 8,9可知:随着格栅位移增加,格栅附近的孔隙率和配位数呈相反的变化趋势,格栅位移较大时,配位数和孔隙率呈稳定波动.这是因为在荷载传递过程中,砂颗粒向筋土界面外侧运动,筋土界面处砂颗粒的接触数减少而孔隙率增加,造成筋土界面处局部剪胀现象,在拉拔端较大的拉拔力作用下,离拉拔端筋土界面越近的砂颗粒剪胀现象越明显,导致了剪胀区域分布不均匀,剪胀区域逐渐发育形成一条局部化的剪胀条带.第3层和第4层测量圆内配位数和孔隙率整体变化微乎其微,表明拉拔力对远离筋土界面的砂颗粒影响不大.
2.3 颗粒的运动与剪切带为了分析筋土界面处剪切带的发生机制和演化过程,在细观层面可以通过颗粒的位移和旋转表征.由图 8,9可知,在格栅纵向50~200 mm范围内,剪切带的剪胀规律基本一致,图 10为在不同的格栅位移条件下,此范围内沿试样高度方向每隔5 mm计算玻璃砂颗粒的水平位移平均值.从图 10可知,在试样高度方向63 mm以下和85 mm以上,颗粒的平均水平位移较小;高度为63~85 mm的平均水平位移分布曲线出现较大的突变,由此可以推断试样剪切带的平均厚度L≈22 mm,由筋土界面向外玻璃砂颗粒位移值逐渐变小.根据级配分布知平均粒径D50=3.2 mm,剪切带厚度为平均粒径的6.9倍,该比值与文献[14]中L/D50=2~8基本一致,上界面约为平均粒径的3.75倍,下界面约为平均粒径的3.13倍,格栅上界面剪切带厚度略大于下界面.

|
图 10 颗粒的水平位移平均值随试样高度的变化 Fig. 10 Changes of the mean horizontal displacement of particles with the height of the specimen |
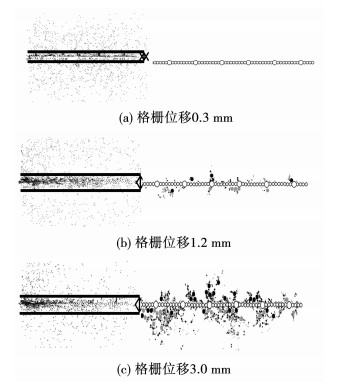
PFC2D可以记录数值试样中颗粒位移和旋转,研究内部剪应变和体应变局部化现象.图 11中颗粒旋转通过PFC2D程序采用FISH语言开发的颗粒旋转颜色显示程序.在拉拔试验中通过开发的程序将颗粒的颜色标记为黑色和灰色(其中黑色代表顺时针旋转,灰色代表逆时针旋转),记录数值试验中颗粒的旋转量.图 11(a)~(c)依次为颗粒旋转量与格栅位移矢量关系的演化图.在试验开始时,通过程序将试样内颗粒的旋转量清零,将模型内所有颗粒标记为白色.
|
图 11 颗粒旋转量与格栅位移矢量的分布演化 Fig. 11 Distribution and evolution of particle rotation and geogrid displacement vector |
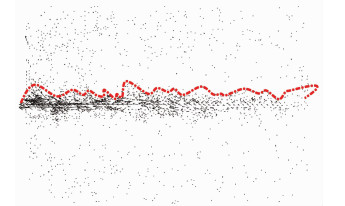
由图 11可知,随着格栅的拔出,拉拔力克服界面颗粒间的滑动摩擦,使玻璃砂颗粒沿着土工格栅表面运动.由于筋土界面中玻璃砂颗粒经历了不同的旋转过程,格栅上下表面的玻璃砂颗粒呈现不同的颜色,这与文献[12]研究结果一致.在土工格栅纵轴上多数为发生了顺时针旋转的黑色玻璃砂颗粒,下方多数为灰色玻璃砂颗粒经历了逆时针的旋转.由图 11(a)~(c)可以看出,随着格栅位移增加,砂颗粒位移场和旋转场逐渐向格栅纵轴后延伸,格栅位移较大时,砂颗粒位移场和旋转场分布不再随着格栅位移增加而增加,最后砂颗粒整体的滑移形成了一个稳定的剪切带,且随着砂颗粒与剪切带距离增加,砂颗粒的旋转量和位移量都逐渐减小.从位移矢量详图 12可以发现,沿格栅纵轴方向剪切带厚度不一致,剪切带边缘呈“锯齿”分布,由此可见颗粒不同的位移量和旋转量影响了剪切带的分布形状.图 11也证明了图 8和9中的结论,格栅位移增加时,筋土界面中玻璃砂颗粒的位移和旋转增加,导致测量圆内颗粒接触数减少和孔隙率的增加,揭示了试样宏观的体积剪胀主要受剪切带内颗粒的运动控制.
|
图 12 格栅位移3 mm时砂颗粒位移矢量详图 Fig. 12 Details of the particle displacement vectors at geogrid displacement of 3 mm |
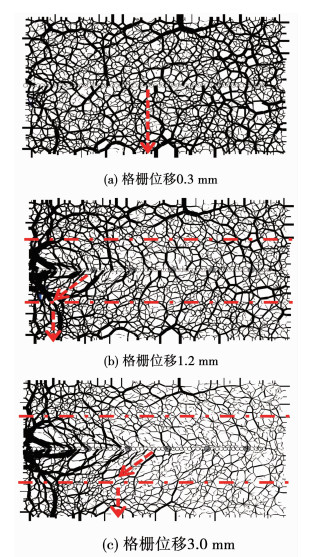
接触力链分布特征是筋土界面颗粒间荷载传递特性的本质体现[16].在剪切阶段,剪切带的演化与筋土界面内力链分布有很大联系.图 13(a)~(c)为试样中玻璃砂颗粒间力链的演化图,在图 13中颗粒间的接触力用黑线表示,接触力链的粗细与颗粒间接触力大小成比例.图 13(a)中当土工格栅位移较小时,颗粒间的接触力网络分布均匀,整体接触力的方向大致呈竖向分布.由图 13(b)可知,随着格栅位移的增加,格栅单元上的拉拔力增大,粒间荷载相互传递导致了筋土界面处接触力网络改变,靠近拉拔盒左边界的力链逐渐与土工格栅形成一定的偏转角,同时强力链逐渐沿着格栅纵轴方向向后延伸.图 13(c)显示,整段格栅上都出现倾斜力链分布.通过分析可知,剪切带内主要为倾斜的强力链网络,呈“八字型”分布.剪切带外受格栅拉拔力影响较小,多数为弱力链网络,呈竖向分布.格栅位移较大时,剪切带内外力链分布形状趋于稳定,由此说明了筋土界面处力链网络分布维持了剪切带的形状.
|
图 13 拉拔模型的力链演化图 Fig. 13 Force chain distribution in pull-out model |
为了分析剪切带中细观组构的演化规律和宏观变形特征之间的联系,将剪切带中大主应力方向分布规律和细观组构参数的演化规律进行对比研究.图 14为格栅拔出阶段模型内大主应力方向和剪切带中细观组构的演化图,其中虚线代表剪切带中大主应力方向.通过测量圆获取模型内的应力分量,根据模型内主应力分量计算大主应力方向的分布规律,其中大主应力方向θ计算表达式为
| $ \theta = \frac { 1 } { 2 } \arctan \left( \frac { - 2 \tau _ { x y } } { \sigma _ { x x } - \sigma _ { y y } } \right). $ | (2) |

|
图 14 大主应力方向和细观组构的演化关系 Fig. 14 Evolution of inclination of major principal stress and fabric anisotropy |
式中:τxy为切向力;σxx为x轴方向的应力;σyy为y轴方向的应力.
格栅拔出过程中伴随着颗粒间接触的崩解和重构,以及粒间接触力的大小和分布也会出现连续的演化.本文通过获取剪切带中颗粒间接触的数据,通过Rothenburg和Bathurst[17]提出的傅里叶近似法(Fourier series approximation,FSA)分析细观组构各向异性的演化,其表达式分别为
| $ E ( \theta ) = \frac { 1 } { 2 \pi } \left[ 1 + a _ { \mathrm { c } } \cos 2 \left( \theta - \theta _ { \mathrm { c } } \right) \right], $ | (3) |
| $ f _ { \mathrm { n } } ( \theta ) = f _ { 0 } \left[ 1 + a _ { \mathrm { n } } \cos 2 \left( \theta - \theta _ { \mathrm { n } } \right) \right], $ | (4) |
| $ f _ { \mathrm { t } } ( \theta ) = - f _ { 0 } a _ { \mathrm { t } } \sin 2 \left( \theta - \theta _ { \mathrm { t } } \right), $ | (5) |
| $ f _ { 0 } = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } f _ { \mathrm { n } } ( \theta ) \mathrm { d } \theta. $ | (6) |
式中:E(θ),fn(θ)和ft(θ)分别为接触法向、法向接触力和切向接触力密度分布函数;f0为法向接触力均值;θc,θn和θt分别为接触法向、法向接触力和切向接触力各向异性方向;ac,an和at分别为接触法向、法向接触力和切向接触力各向异性系数.
由图 14(a)~(c)可知,当格栅位移较小时,加载板上应力大于格栅上的拉拔应力,竖直方向应力较大,剪切带中的大主应力方向接近竖向分布.随着格栅位移的增加,大主应力方向逐渐从竖直方向向右偏转,然后偏转角度逐渐趋于稳定.剪切带外大主应力方向变化较小.通过观察图 13,14可知,随着格栅位移的增加,大主应力方向和力链网络分布有相同的演化趋势.
为了分析拉拔过程中细观组构各向异性的变化规律,针对剪切带区域的组构各向异性参数进行统计,如图 14所示,其中虚线为式(3)~(6)傅里叶函数的拟合结果,定义经过原点带有箭头的实线代表组构各向异性的主方向.在统计区域内以10°为一分区对各分区的组构各向异性进行统计,定义M为剪切带内总接触数,ΔM(θ)/MΔ(θ)为各角度区域接触数与总接触数的比.由图 14(a)可知,在格栅位移为0.3 mm时,拟合ac=0.050 1,θc=90.72°;an=0.052 2,θn=110.02°,实测和拟合的接触法向和平均法向接触力分布形状均接近“圆形”,表明此时剪切带内颗粒间接触和法向接触力分布的各向异性程度不明显,可以推断统计区域呈现各向同性.切向接触力组构参量拟合at=0.028 4,θt=128.75°,拟合后切向接触力峰值与各向异性主方向对称,切向接触力各向异性主方向上平均切向接触力为零,切向接触力各向异性呈“蝴蝶状”分布.
通过分析图 14(b)可以看出,当格栅位移增加到1.2 mm时,法向接触力的主方向θn发生明显偏转,拟合an=0.288 9,θn=133.60°,此时法向接触力各向异性呈“椭圆”分布,法向接触力出现各向异性变化.由图 14(c)可知,在格栅位移为3 mm时,格栅上的拉拔力增加,在剪切带中产生较大的水平应力,拟合an=0.416 5,θn=130.07°,此时法向接触力各向异性呈“花生状”分布,局部剪胀增加,剪切带中颗粒法向接触力各向异性增加.对比图 14(c)中大主应力方向,平均法向接触力各向异性主方向与其方向相近.
由图 14(a)~(c)中组构各向异性参数(ac, an, at)拟合结果对比可知,在格栅拉拔位移较小时,随着格栅位移的增加,剪切带中ac变化较小,说明颗粒间接触数变化不明显.而an和at均随着格栅拉拔位移增加而显著增加,且an和at变化趋势与拉拔阻力的变化规律相似.由上述规律可得出结论:拉拔过程中,剪切带内颗粒间切向接触力和法向接触力演化形式影响其密实度和颗粒配位数,进而导致试样的局部剪胀和减缩现象.
图 15为拉拔过程中,剪切带内组构参量主方向与大主应力方向的变化曲线.当格栅位移小于1.2 mm时,剪切带内θ波动较大,θ明显增加,大主应力方向随着格栅位移增加逐渐稳定在125°~135°.当格栅位移超过1.2 mm时,剪切带内θ、θn和θt的角度变化大致相同,三者角度稳定在125°~135°,表明大主应力方向与接触力各向异性主方向的偏转角度存在一定关联,格栅拉拔过程中宏观拉拔力受剪切带中接触力的分布及其各向异性的影响.
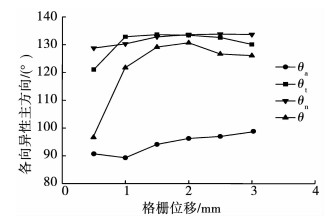
|
图 15 组构参量主方向变化曲线 Fig. 15 Variation of fabric anisotropy parameters |
1) 剪切带中平均孔隙率与平均配位数呈负相关.在拉拔过程中,筋土界面区域孔隙率持续增加而配位数减少,表明了剪切带细观参数的变化影响试样整体的剪胀性.
2) 拉拔阶段颗粒的旋转主要集中在剪切带中,沿着土工格栅界面两侧颗粒的旋转方式不相同.格栅位移较大时,筋土界面区颗粒的整体位移和旋转形成了一个稳定的剪切区,剪切区平均厚度基本不变,呈“锯齿”分布.
3) 由力链分析可知,随着格栅位移增加,颗粒间接触力的传递过程伴随着力链网络的演化.当格栅位移较大时,剪切带中力链网络的分布形状随着格栅位移增加基本不变,并且强力链多集中在剪切带中,筋土界面内部力链网络维持了剪切带的基本形状.
4) 试样内部颗粒间法向接触力分布及其各向异性的演化反映了试样的宏观变形情况,剪切带中颗粒间主应力方向的变化与接触力各向异性主方向的变化同步.反映了颗粒间接触力的分布及其各向异性演化在一定程度上决定了玻璃砂颗粒的宏观力学性质.
| [1] |
ALAGIYAWANNA A M N, SUGIMOTO M, SATO S, et al. Influence of longitudinal and transverse members on geogrid pullout behavior during deformation[J]. Geotextiles and Geomembranes, 2001, 19(8): 483. DOI:10.1016/S0266-1144(01)00020-6 |
| [2] |
LI H L, CHEN Y J, PEDRO F, et al. Experimental investigations on the pull-out behavior of tire strips reinforced sands[J]. Materials, 2017, 10(7): 707. DOI:10.3390/ma10070707 |
| [3] |
FARRAG K, ACAR Y B, JURAN I. Pull-out resistance of geogrid reinforcements[J]. Geotextiles and Geomembranes, 1993, 12(2): 133. DOI:10.1016/0266-1144(93)90003-7 |
| [4] |
SUGIMOTO M, ALAGIYAWANNA A M, KADOGUCHI K. Influence of rigid and flexible face on geogrid pullout tests[J]. Geotextiles and Geomembranes, 2001, 19(5): 257. DOI:10.1016/S0266-1144(01)00011-5 |
| [5] |
EZZEIN F M, BATHURST R J. A new approach to evaluate soil-geosynthetic interaction using a novel pullout test apparatus and transparent granular soil[J]. Geotextiles and Geomembranes, 2014, 42(3): 246. DOI:10.1016/j.geotexmem.2014.04.003 |
| [6] |
陈榕, 栾茂田, 赵维, 等. 土工格栅拉拔试验及筋材摩擦受力特性研究[J]. 岩土力学, 2009, 30(4): 960. CHEN Rong, LUAN Maotian, ZHAO Wei, et al. Research on pull-put test and frictional resistance characteristic of geogrids[J]. Rock and Soil Mechanics, 2009, 30(4): 960. DOI:10.16285/j.rsm.2009.04.040 |
| [7] |
闫澍旺, BARRB. 土工格栅与土相互作用的有限元分析[J]. 岩土工程学报, 1997, 19(6): 56. YAN Shuwang, BARR B. Finite-element modelling of soil-geogrid interaction with application to interpret the pullout behaviour of geogrids[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(6): 56. DOI:10.3321/j.issn:1000-4548.1997.06.011 |
| [8] |
SIRIWARDANE H, GONDLE R, KUTUK B, et al. Experimental investigation and numerical analysis of reinforced geologic media[C]//The 12th International Conference on Computer Methods and Advances in Geomechanics (IACMAG). Goa, India: [s.n.], 2008: 4369
|
| [9] |
HUSSEIN M G, MEGUID M A. Three-dimensional finite element analysis of soil-geogrid interaction under pull-out loading condition[C]//The 66th Canadian Geotechnical Conference. Montreal, Canada: [s.n.], 2013: 452
|
| [10] |
周健, 孔祥利, 鞠庆海, 等. 土工合成材料与土界面的细观研究[J]. 岩石力学与工程学报, 2007, 26(增刊1): 3196. ZHOU Jian, KONG Xiangli, JU Qinghai, et al. Mesoscopical study on interface between geosynthetics and soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 1): 3196. |
| [11] |
陈建峰, 李辉利, 柳军修, 等. 土工格栅与砂土的细观界面特性研究[J]. 岩土力学, 2011, 32(增刊1): 66. CHEN Jianfeng, LI Huili, LIU Junxiu, et al. Mesoscopic study of interface properties of geogrid-reinforced soil[J]. Rock and Soil Mechanics, 2011, 32(Suppl 1): 66. DOI:10.16285/j.rsm.2011.s1.115 |
| [12] |
WANG Z, JACOBS F, ZIEGLER M. Visualization of load transfer behaviour between geogrid and sand using PFC2D[J]. Geotextiles and Geomembranes, 2014, 42(2): 83. DOI:10.1016/j.geotexmem.2014.01.001 |
| [13] |
苗晨曦, 郑俊杰, 崔岚, 等. 格栅-砂土界面宏细观关联性与加筋性能评价方法研究[J]. 岩石力学与工程学报, 2011, 32(增刊1): 3249. MIAO Chenxi, ZHENG Junjie, CUI Lan, et al. Study of the macro-meso correlation of geogrid-soil interface and assessment method of reinforced performance[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 32(Suppl 1): 3249. DOI:10.13722/j.cnki.jrme.2014.1433 |
| [14] |
FERREIRA J A Z, ZORNBERG J G. A transparent pullout testing device for 3D evaluation of soil-geogrid interaction[J]. Geotechnical Testing Journal, 2015, 38(5): 686. DOI:10.1520/GTJ20140198 |
| [15] |
LAI H J, ZHENG J J, ZHANG J, et al. DEM analysis of "soil-arching" within geogrid-reinforced and unreinforced pile-supported embankments[J]. Computers and Geotechnics, 2014, 61: 13. DOI:10.1016/j.compgeo.2014.04.007 |
| [16] |
孙其诚, 辛海丽, 刘建国, 等. 颗粒体系中的骨架及力链网络[J]. 岩土力学, 2009, 30(增刊1): 83. SUN Qicheng, XIN Haili, LIU Jianguo, et al. Skeleton and force chain network in static granular material[J]. Rock and Soil Mechanics, 2009, 30(Suppl 1): 83. DOI:10.16285/j.rsm.2009.s1.006 |
| [17] |
ROTHENBURG L, BATHURST R J. Analytical study of induced anisotropy in idealized granular materials[J]. Géotechnique, 1989, 40(39): 665. |
 2019, Vol. 51
2019, Vol. 51


