2. 中铁一院集团山东建筑设计院有限公司,山东 青岛 266031
2. Shandong Institute of Architectural Design Co., Ltd., of China Railway First Design Institute Group, Qingdao 266031, Shandong, China
近年来,中国城市建设发展快速,城市地下工程的施工不可避免地会对城市已有地表及地下设施产生影响,引发路面坍塌等工程灾害.在地下空间建设过程中注浆工艺对地层加固、减少地层沉降等具有重要作用,注浆工程中主要靠压密注浆和劈裂注浆对上覆围岩进行抬升.EI-Kelesh等[1]利用圆孔扩张方法及介质锥形破坏方法建立了压密注浆造成的地表抬升数学模型.章敏等[2]根据随机介质方法建立了多个压密浆脉造成地表抬升位移的计算公式,并对计算方法进行了简化.李立新等[3]把微元体引起地表的总抬升量假设为单一压密浆脉造成的地表抬升量,同样根据随机介质方法得到了单一压密浆脉造成的地表抬升位移的计算公式.
通过室内实验可以验证注浆引起的地表抬升理论.Soga等[4]研制了注浆抬升实验系统,利用该系统研究了注浆引起抬升的长效因素.郑刚等[5]分别分析了开挖扰动和注浆对周围土体位移的影响,并开展了室内试验进行了验证.张晓双[6]设计了在成层黏土、结构性黏土、欠固结黏土等介质中注浆的抬升机理实验系统.冯旭海[7]提出了注浆引起的地表抬升的计算方法,研究了注浆抬升过程土体介质中力的分布,并通过实验进行了验证.为了验证注浆抬升在实际工程中的影响,有些学者在实际注浆工程中做了相关现场试验.侯艳娟等[8]在工程现场研究了建筑发生显著位移时的注浆参数,并记录了最大位移值.郭乐等[9]采用全断面和分层2种注浆方式进行现场实验,研究了注浆对路基抬升的影响.逄铁铮[10]对拆迁房进行了注浆实验,研究建筑地基在注浆加固过程中的抬升规律.许多学者通过软件研究了注浆引起的土体抬升.Sharghi[11]研究了浆液对地表沉降的影响,并利用FLAC3D软件对两种组分浆液进行了适量、抗压强度的数值模拟.Ochmański[12]采用三维有限元模型对地面沉降进行了分析,并对土体的非线性进行了精确模拟.Nicolini等[13]通过软件设置方向不同、大小不同的应变来代替注浆引起的介质位移变化. Schweiger等[14]使用相同方法,在标定注浆范围内的单元体施加体积应变来模拟注浆过程,并通过增加注浆区和周围影响区内单元的刚度来模拟注浆抬升效果.Ni等[15]采用PLAXIS2D数值模拟软件在注浆单元体内施加体应变研究注浆抬升.可以通过设置应变来模拟注浆,还可以设置扩张力来代替注浆过程.唐智伟等[16]设置了单元体内的扩张力来模拟注浆过程.张冬梅等[17]通过软件模拟了运营期隧道横向注浆引起的围岩土体横向位移.孙锋等[18]设置了单元体内的扩张力来模拟浆液引起的管道抬升规律.
本文在已有注浆抬升理论基础上提出了压密注浆和劈裂注浆造成的地表抬升位移的计算方法及其简化计算方法,并进行了室内实验及数值模拟.该计算方法适用于城市浅埋小净距土质中墙隧道注浆后的地表抬升预测,简化算法能大大提高计算效率.施工过程中根据预测结果进行注浆参数设计,可以防止注浆引起的抬升对地表的破坏,实现软弱地层的有效加固.
1 注浆抬升计算方法按照浆液扩散形式可以将浆液扩散分为压密注浆、劈裂注浆、渗透注浆3种类型,根据水平地应力和竖直地应力的大小关系可以将劈裂注浆分为水平劈裂注浆扩散和竖直劈裂注浆,其中竖直劈裂注浆对土体水平方向的挤压效果明显,对地表抬升影响较小.渗透注浆主要针对砂质地层、卵石或岩石裂隙等孔隙率较大的介质体,作用为填充地层孔隙,同样对地表抬升影响较小.本文主要研究了球形压密注浆和水平劈裂注浆对地表抬升的影响规律,这两种注浆模型所引起的地表抬升最为明显.
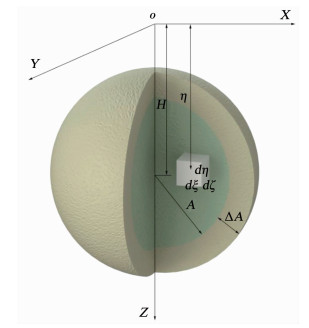
1.1 压密注浆造成地面抬升位移的计算方法应用随机介质方法,可以将压密浆脉假设为各向同性的球形均质体,在压密球形浆脉体积不断膨胀的过程中分解为无数个球形单元体,这些球形单元体膨胀所引起的土体抬升量的总和即为注浆引起的土体抬升位移.图 1为球型浆泡体积膨胀示意.
|
图 1 压密注浆单元模型 Fig. 1 Compaction grouting unit model |
图中H为注浆管口埋深,A为浆泡初始半径,ΔA为浆泡体积膨胀后引起的球体半径增量,η为所分析注浆单元体的埋深,ξ、ζ分别为注浆单元体在X、Y方向的偏移量,注浆引起点(x, y, z)处的竖向抬升位移为[19-20]
| $ W _ {\rm e } = \frac { 1 } { r ^ { 2 } ( z ) } \exp \left[ \frac { - \pi \left( x ^ { 2 } + y ^ { 2 } \right) } { r ^ { 2 } ( z ) } \right] \mathrm { d } \xi \mathrm { d } \zeta \mathrm { d } \eta. $ | (1) |
式中:r(z)为注浆单元体引起地表抬升的主要影响半径,r(z)=z/tan β; β为注浆体注浆引起土体抬升的影响角.根据文献[21]可以得到地表抬升位移为
| $ \begin{array} { c } { W ( x , y , 0 ) = \int _ { a _ { 1 } } ^ { b _ { 1 } } \int _ { c _ { 1 } } ^ { d _ { 1 } } \int _ { e _ { 1 } } ^ { f _ { 1 } } \frac { \tan ^ { 2 } \beta } { \eta ^ { 2 } } \exp \left\{ \frac { - \pi \tan ^ { 2 } \beta } { \eta ^ { 2 } } \right.} \cdot \\ { \left[ ( x - \xi ) ^ { 2 } + ( y - \zeta ) ^ { 2 } \right] \} \mathrm { d } \xi \mathrm { d } \zeta \mathrm { d } \eta - \int _ { a _ { 2 } } ^ { b _ { 2 } } \int _ { c _ { 2 } } ^ { d _ { 2 } } \int _ { e _ { 2 } } ^ { f _ { 2 } } \frac { \tan ^ { 2 } \beta } { \eta ^ { 2 } } } \cdot \\ { \exp \left\{ \frac { - \pi \tan ^ { 2 } \beta } { \eta ^ { 2 } } \left[ ( x - \xi ) ^ { 2 } + ( y - \zeta ) ^ { 2 } \right] \right\} \mathrm { d } \xi \mathrm { d } \zeta \mathrm { d } \eta } .\end{array} $ | (2) |
式中:a1=H-A-ΔA, b1=H+A+ΔA,
| $ { c _ { 1 } = - \sqrt { ( A + \Delta A ) ^ { 2 } - ( H - \eta ) ^ { 2 } } } , $ |
| $ { d _ { 1 } = \sqrt { ( A + \Delta A ) ^ { 2 } - ( H - \eta ) ^ { 2 } } } , $ |
| $ { e _ { 1 } = - \sqrt { ( A + \Delta A ) ^ { 2 } - ( H - \eta ) ^ { 2 } - \zeta ^ { 2 } } }, $ |
| $ f_{1}=\sqrt{(A+\Delta A)^{2}-(H-\eta)^{2}-\zeta^{2}}, $ |
| $ a_{2}=H-A ; b_{2}=H+A, c_{2}=-\sqrt{A^{2}-(H-\eta)^{2}}, $ |
| $ d_{2}=\sqrt{A^{2}-(H-\eta)^{2}}, e_{2}=-\sqrt{A^{2}-(H-\eta)^{2}-\zeta^{2}}, $ |
| $ f_{2}=\sqrt{A^{2}-(H-\eta)^{2}-\zeta^{2}}. $ |
图 1中压密注浆模型的浆泡初始半径A和浆泡体积膨胀后引起的球体半径增量ΔA相对于埋深H为极小值,所以, 浆泡模型可以视作一个微元,把压密注浆造成的地表抬升位移等效为加固区的整体体积和微元体造成的抬升位移量的乘积.文献[3]对注浆抬升数学模型进行了简化,省略了式(2)中复杂的积分计算,简化后的公式如下:
| $ \begin{array}{l}{W(x, y, 0)=\left(\frac{4}{3} \pi(A+\Delta A)^{3}-\frac{4}{3} \pi A^{3}\right) \times} \\ {\frac{\tan ^{2} \beta}{H^{2}} \exp \left[\frac{-\pi \tan ^{2} \beta\left(x^{2}+y^{2}\right)}{H^{2}}\right]=} \\ {\quad \frac{4 \pi \tan ^{2} \beta \Delta A\left(3 A^{2}+3 A \Delta A+\Delta A^{2}\right)}{3 H^{2}} \times} \\ {\quad \exp \left[\frac{-\pi \tan ^{2} \beta\left(x^{2}+y^{2}\right)}{H^{2}}\right]}.\end{array} $ | (3) |
在压密浆脉球体的地面影响范围内,距离球心在地表的投影距离越远抬升位移值越小,球心在地面的投影处的抬升位移值最大,其表达式为
| $ \begin{array}{c}{W_{\max }=W(0, 0, 0)=} \\ {\quad \frac{4 \pi \tan ^{2} \beta \Delta A\left(3 A^{2}+3 A \Delta A+\Delta A^{2}\right)}{3 H^{2}}}.\end{array} $ | (4) |
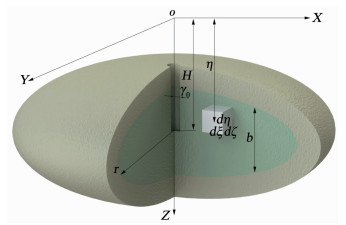
在软弱地层注浆加固过程中,当注浆压力达到启劈压力[22]时,会使地层产生劈裂,劈裂方向为最大主应力σ1的方向[23],由于竖直方向劈裂对地表影响较小,只研究最大主应力为水平方向时的劈裂注浆对地表抬升的影响.假设水平应力大于竖直应力,σ3为最小主应力,劈裂浆脉为厚度变化的水平辐射圆饼,地表任一点到圆心距离相同点的垂直抬升位移相同.如图 2所示,r为圆饼浆脉水平截面圆的初始半径,r0为注浆管半径,b为圆饼浆脉的初始厚度,H为注浆孔的埋深.
|
图 2 劈裂注劈裂浆单元模型 Fig. 2 Fracture grouting unit model |
在图 2圆饼浆脉的坐标系中,根据文献[24]可以得到圆饼浆脉的初始厚度b与圆饼浆脉水平截面圆的初始半径r的关系式如下:
| $ b=\sqrt[4]{\frac{24 G q \mu}{\pi} \ln \left(\frac{r_{\max }}{r}\right)}\left(r_{0} <r <r_{\max }\right). $ | (5) |
式中:G为软如地层介质参数;q为单位时间的注浆量;μ为水泥浆的黏度;rmax为浆液扩散的最大半径,其值与浆液压力有关,即
| $ r_{\mathrm{max}}=r_{0} \exp \left[\frac{\pi G^{3}\left(p_{\mathrm{s}}-\sigma_{3}\right)^{4}}{H^{2}}\right]. $ | (6) |
式中:ps为浆液压力;σ3为最小主应力.
水平辐射圆饼浆脉所引起的地面抬升量为土体劈裂所导致的地面抬升量和浆液水平扩散之前半径为r0浆球所造成的地面抬升量之差,表达式为
| $ W(x, y, 0)=\int_{a_{3}}^{b_{3}} \int_{c_{3}}^{d_{3}} \int_{e_{3}}^{f_{3}} \frac{\tan ^{2} \beta}{\eta^{2}} \exp \left\{\frac{-\pi \tan ^{2} \beta}{\eta^{2}}\right. \cdot \\ \left[(x-\xi)^{2}+(y-\zeta)^{2}\right] \}_{\mathrm{d} \xi \mathrm{d} \zeta \mathrm{d} \eta}-\\\int_{a_{4}}^{b_{4}} \int_{c_{4}}^{d_{4}} \int_{e_{4}}^{f_{4}} \frac{\tan ^{2} \beta}{\eta^{2}} \exp \left\{\frac{-\pi \tan ^{2} \beta}{\eta^{2}}\right.\cdot \\\left[(x-\xi)^{2}+(y-\zeta)^{2}\right] \}_{\mathrm{d} \xi \mathrm{d} \zeta \mathrm{d} \eta}. $ | (7) |
取值范围如下:a3=H-bmax, b3=H+bmax,
| $ c_{3}=-\sqrt{r_{\max }^{2}\left[1-\frac{(\eta-H)^{2}}{b_{\max }^{2}}\right]}, $ |
| $ d_{3}=\sqrt{r_{\max }^{2}\left[1-\frac{(\eta-H)^{2}}{b_{\max }^{2}}\right]}, $ |
| $ e_{3}=-\sqrt{r_{\max }^{2}\left[1-\frac{(\eta-H)^{2}}{b_{\max }^{2}}\right]-\zeta^{2}}, $ |
| $ f_{3}=\sqrt{r_{\max }^{2}\left[1-\frac{(\eta-H)^{2}}{b_{\max }^{2}}\right]-\zeta^{2}}, $ |
| $ a_{4}=H-r_{0}, b_{4}=H+r_{0}, c_{4}=-\sqrt{r_{0}^{2}-(H-\eta)^{2}}, $ |
| $ d_{4}=\sqrt{r_{0}^{2}-(H-\eta)^{2}}, $ |
| $ e_{4}=-\sqrt{r_{0}^{2}-(H-\eta)^{2}-\zeta^{2}}, $ |
| $ f_{4}=\sqrt{r_{0}^{2}-(H-\eta)^{2}-\zeta^{2}}. $ |
为了省略式(7)中复杂的积分计算,参考压密注浆抬升位移量计算方法的简化,将加固区视作一个微元,把劈裂注浆造成的地表抬升位移等效为加固区的整体体积和微元体造成的抬升位移量的乘积.圆饼可设为长轴为rmax、短轴为bmax的椭圆绕短轴旋转一周形成的椭球体,简化后的地表抬升公式为
| $ \begin{array}{c}{W(x, y, 0)=\left(\frac{4}{3} \pi r_{\max }^{2} b_{\max }-\frac{4}{3} \pi r_{0}^{3}\right) ) \times \frac{\tan ^{2} \beta}{H^{2}}} \cdot \\ {\exp \left[\frac{-\pi \tan ^{2} \beta\left(x^{2}+y^{2}\right)}{H^{2}}\right]=\frac{4 \pi \tan ^{2} \beta\left(r_{\max }^{2} b_{\max }-r_{0}^{3}\right)}{3 H^{2}}} \cdot \end{array}\\ \exp \left[\frac{-\pi \tan ^{2} \beta\left(x^{2}+y^{2}\right)}{H^{2}}\right]. $ | (8) |
由式(8)可知,在地表距浆脉圆饼地表投影的中心点距离越近,地面抬升位移量就越大,且当D相等时
| $ W_{\max }=W(0, 0, 0)=\frac{4 \pi \tan ^{2} \beta\left(r_{\max }^{2} b_{\max }-r_{0}^{3}\right)}{3 H^{2}}. $ | (9) |
为了验证压密注浆和劈裂注浆引起地面抬升位移量的计算公式及其简化公式,设计了室内球形压密注浆和劈裂注浆模型实验.实验被注介质为土,浆液为两种水灰比的水泥单液浆,采集注浆过程中的地表位移量和土压力,研究注浆参数对注浆抬升位移量的影响及注浆抬升过程,室内注浆模型实验系统如图 3所示.

|
图 3 注浆模型实验系统 Fig. 3 Experiment system for the grouting model |
实验模型箱由亚克力板箱和钢结构外框构成,注浆设备为MY-JD3242型注浆泵及其控制系统.数据监测系统包括KTR2-50型位移传感器、土压传感器、渗压传感器、CCD相机等.9个位移传感器按照3×3方阵布置,每隔100 mm一个,位移、土压、渗压数据由XL2101G型静态电阻应变仪接收.辅助装置包括水平尺、偏光激光仪,用来保证土体表面的初始水平.
2.2 实验材料参数标定注浆加固抬升实验用土取自某施工现场,对所取土样的密度、无侧限抗压强度、抗剪强度、液塑限进行实验测定,得到表 1中实验用土的参数.本实验中所用水泥为济南某水泥厂生产的P.O.32.5普通硅酸盐水泥,其性能指标见表 2.
| 表 1 原状土基本物理力学参数 Tab. 1 Basic physical and mechanical parameters of undisturbed soil |
| 表 2 试验用注浆材料主要性能指标 Tab. 2 Performance of the grouting material used in experiment |
在压密注浆模型试验中,为了实现球形压密注浆,注浆出口处绑定一个球形气囊,在注浆过程中浆液填满气囊使其呈球形膨胀.选取实验用土的干密度、注浆口的埋深及实验用土的含水率为压密注浆模型实验的考察因素.实验用土干密度ρs采用1.07,1.27及1.47 g/cm33种,注浆口的埋深H分别设置150,200及250 mm 3种,实验用土的含水率w采用12%,15%及18% 3种,考虑3种影响因素共实验27组.
2.3.2 劈裂注浆模型实验土体填充为水平方向逐层压实填充,使水平应力为最大主应力,从而得到水平劈裂浆脉.劈裂注浆模型实验同样选取实验用土的干密度、注浆口的埋深及实验用土的含水率为劈裂注浆模型实验的考察因素,条件取值与压密实验方案一致,考虑3种影响因素共实验27组.
2.4 实验结果 2.4.1 注浆实验抬升现象根据注浆实验抬升现象的记录可知,在注浆量不断增大的过程中,土体表面发生逐渐抬升现象,注浆管口在土体表面的投影处抬升位移量最大,距离投影点的位置越远抬升位移量越小.图 4(a)中线条标出了压密注浆影响的土层变形范围,图 4(b)中线条标出了劈裂注浆的土层变形范围,可以发现,压密注浆导致的地表最大抬升量要比劈裂注浆大,劈裂注浆地表土层抬升范围要比压密注浆大.

|
图 4 注浆引起的地表抬升 Fig. 4 Surface uplift caused by grouting |
在本文实验中,影响地表抬升最大位移Wmax的因素主要有H、ρs、w,为了研究各因素与Wmax的相关性,引入抬升系数γ1.在压密注浆中令Wmax=γ1Rmax,Rmax为球型浆泡的最大半径,其中0<γ1<1,表 3为压密注浆过程统计参数.
| 表 3 压密注浆实验参数及抬升系数γ1 Tab. 3 Compaction grouting experimental parameters and uplift coefficient γ |
采用Minitab 16统计软件对γ1与H、ρs、w,进行回归拟合,可得其关系为
| $ r_{1}=0.52-0.00713 \rho_{\rm s}+0.147 H-0.00956 w. $ | (10) |
经过计算R2=97.2%,拟合公式的标准化残差分布服从正态分布,上述公式拟合较好,有较好的统计意义.
对于劈裂注浆地表抬升实验,令γ2为注浆抬升土层引起的地表抬升最大位移Wmax与水平劈裂圆饼浆脉最大厚度bmax的比值,即Wmax=γ2bmax,γ2的取之范围为0<γ2<1,表 4为劈裂注浆过程统计参数.可得拟合公式为
| $ \gamma_{2}=0.748-0.00839 \rho_{\rm s}+0.165 H-0.0123 w. $ | (11) |
| 表 4 劈裂注浆实验参数及抬升系数γ2 Tab. 4 Fracture grouting experimental parameters and uplift coefficient γ2 |
计算可得R2=97.2%,拟合公式的标准化残差分布服从正态分布,式(11)同样拟合较好,有较好的统计意义.两种注浆方式的回归分析表明,H对抬升的影响最大.
3 数值模拟 3.1 数值模拟参数设置为验证注浆抬升的数学模型,采用数值模拟软件模拟不同注浆口埋深引起的地表抬升.本文选用PFC数值计算软件对球形压密注浆和水平劈裂注浆所造成的地面抬升现象进行竖直模拟,采用伺服机制设置浆液压力,使用颗粒流方法、Fish语言模拟注浆过程.研究注浆抬升造成的土体位移场及应力场的变化.根据下列5条假定来进行数值模拟:1)颗粒流模拟所使用的单元为球体或圆饼,单元在外力作用下可进行移动、旋转及分离;2)颗粒流模拟所使用的单元相互为点接触;3)颗粒流模拟所使用的单元体为刚性,颗粒单元的切向刚度及法向刚度可以任意设置;4)颗粒流模拟所使用的单元相互柔性接触,当作用力为压力时单元之间可以重叠,其重叠量随作用力增大而增大,但远小于颗粒单元的大小;5)颗粒流模拟所使用的单元之间设黏结强度.
模型设置包括球体颗粒与不透水边界,经过对模型实验中实验土体进行级配分析、单轴压缩及三轴压缩数值实验,对被注介质进行土体的最小颗粒半径Rmin、最大半径与最小半径比值Rmax/Rmin、密度ρ、弹性模量E、内摩擦角φ、黏聚力c、泊松比v等物理参数通过测试标定如表 5,球体颗粒随机分布于模型空间之内,设计3种注浆深度H取值分别为150,200,250 mm,被注介质的基本参数、注浆体膨胀半径等均相等.在注浆孔外设定一个球体墙,墙内侧设置注浆压力,在注浆压力作用下墙不停向外侧扩张,即模拟了浆脉的膨胀过程.
| 表 5 土体物理参数 Tab. 5 Physical parameters of the soil |
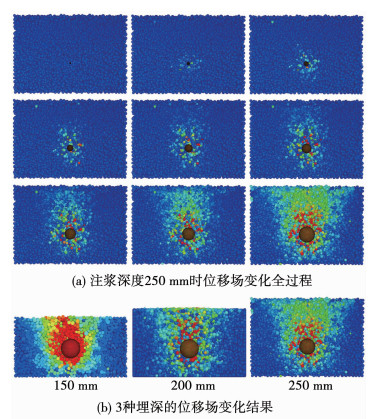
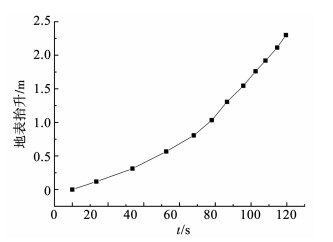
图 5为注浆深度H取值在250 mm时模拟注浆位移场变化的全过程和3种H的位移场,浆泡膨胀引起的抬升影响区域接近于锥形体.从模拟结果可知,随注浆埋深H的增大注浆所造成的抬升位移量减小;随注浆埋深H的增大地表抬升范围逐渐增大. 图 6为注浆深度在250 mm时浆泡在地表投影的中心点位移变化曲线,可以看出,随着注浆量的增加注浆抬升最大位移量不断增大,增长速率越来越快.
|
图 5 压密注浆土体位移场数值模拟 Fig. 5 Numerical simulation of soil displacement field of compaction grouting |
|
图 6 注浆深度在250 mm时地表位移随时间的变化 Fig. 6 Surface displacement over time when the grouting depth is 250 mm |
图 7为模拟劈裂注浆引起地表抬升的位移场图,最大地表竖向位移发生在地表浆脉圆饼投影的中心处,并随着两侧距中心点的距离越大而逐渐减小.相对压密注浆,劈裂注浆影响范围更广.

|
图 7 劈裂注浆土体位移场数值模拟 Fig. 7 Numerical simulation of soil displacement field of fracture grouting |
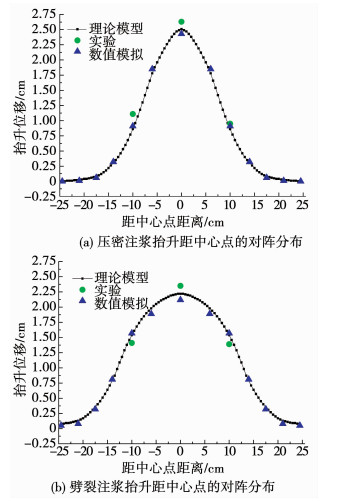
通过球形压密注浆和水平劈裂注浆的室内模型试验及数值模拟可以看出,过注浆孔垂直于地面上的抬升面曲线表现为单峰形态,曲线关于中心点对称,符合基于随机介质理论的压密注浆、劈裂注浆导致的地表抬升量计算方法所显示的规律.图 8同时显示了数值计算曲线、数值模拟监测点位移值、实验监测点位移值,由于实验埋深较浅,采用未简化的数学模型,峰值及变化规律基本相同,因此,验证了数学模型和模拟模型的准确性.
|
图 8 注浆抬升距中心点的对阵分布 Fig. 8 Contrast distribution of grouting lift from center point |
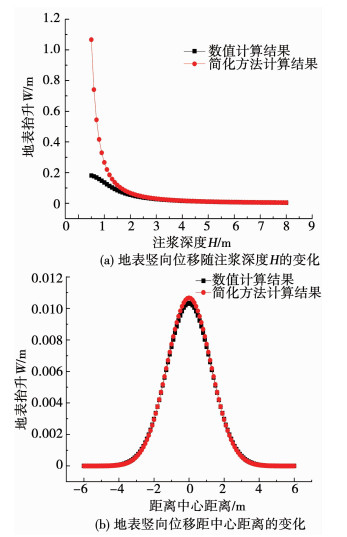
以劈裂注浆为例,为了验证简化计算方法的准确性,依照Legendre-Gauss积分方法采用MATLAB软件编辑计算程序.设计计算程序的参数:r0为0.05 m,rmax为0.5 m,bmax为1 m,tan β为1.6,分别采用劈裂注浆抬升位移量计算方法及其简化方法得到的地表抬升位移量,抬升位移量与H的关系图线如图 9(a)所示,注浆埋深为5 m时抬升位移量分布曲线对比如图 9(b)所示.
|
图 9 数值计算与简化计算结果对比 Fig. 9 Comparison between numerical calculation and simplified calculation |
由图 9(a)可知,当注浆孔埋深在2 m以内时,注浆位移抬升计算方法及其简化方法所得到的抬升位移量偏差较大,前者计算结果明显小于后者;当注浆孔埋深在2 m以上时,注浆位移抬升计算方法及其简化方法所得到的抬升位移量无偏差,所以,简化方法只适用于注浆深度在2 m以上时的工况使用.由图 9(b)注浆孔埋深为5 m时注浆抬升量的分布曲线可知,注浆位移抬升计算方法及其简化方法所得到的注浆抬升位移量曲线基本吻合,注浆抬升最大位移量误差仅为0.000 3 m.
4 结论1) 分析了注浆导致地表抬升的力学机理,并得到了压密注浆、劈裂注浆导致地表抬升位移量的计算方法及其简化算法.
2) 两种注浆方式引起的地表抬升与数学模型计算结果、数值模拟结果吻合性较好;通过对注浆抬升系数γ的回归分析,得到抬升系数的表达式,注浆深度、土体干密度及含水率等因素均影响注浆引起的地表最大抬升量,其中注浆深度影响最大.
3) 数值模拟验证了压密注浆、劈裂注浆导致的地表抬升位移量的计算方法及其简化算法的准确性,单孔注浆使上覆倒锥形土体位移场发生变化,两种注浆方式对比来看,压密注浆地表最大抬升较大,劈裂注浆影响范围较大.
| [1] |
EL-KELESH A M, MOSSAAD M E, ISMAIL M. Model of compaction grouting[J]. Canadian Metallurgical Quarterly, 2001, 127(11): 955. DOI:10.1061/(asce)1090-0241(2001)127:11(955) |
| [2] |
章敏, 刘军军, 秦文权. 注浆抬升位移预测及简化模型研究[J]. 太原理工大学学报, 2015, 46(3): 298. ZHANG Min, LIU Junjun, QIN Wenquan. Prediction and simplified model of uplift displacement by grouting[J]. Journal of Taiyuan University of Technology, 2015, 46(3): 298. DOI:10.16355/j.cnki.issn1007-9432tyut.2015.03.010 |
| [3] |
李立新, 童无欺, 邹金锋. 注浆抬升位移的随机介质理论预测方法[J]. 铁道科学与工程学报, 2013, 10(5): 47. LI Lixin, TONG Wuqi, ZOU Jinfeng. Study on grouting uplift displacement prediction using stochastic medium theory[J]. Journal of Railway Science and Engineering, 2013, 10(5): 47. DOI:10.19713/j.cnki.43-1423/u.2013.05.009 |
| [4] |
CHEONG M T, SOGA K. Influence of underground excavation on compensation grouting in clays; Small-scale laboratory experiments[C]// 5th International Conference on Getechnical Aspects of Underground Construction in Soft Ground. Amsterdam, Netherlands: Int Soc Soil Mech & Geotech Engn, TC 28, 2006: 369. DOI: 10.1201/noe0415391245.ch49
|
| [5] |
郑刚, 张扶正, 张天奇, 等. 盾构隧道开挖及补偿注浆对地层扰动影响的室内试验及数值模拟研究[J]. 岩土工程学报, 2016, 38(10): 1741. ZHENG Gang, ZHANG Fuzheng, ZHANG Tianqi, et al. Disturbance of shield tunnel excavation and compensation grouting to surrounding soil: Laboratory tests and numerical simulations[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1741. DOI:10.11779/CJGE201610001 |
| [6] |
张晓双.地下工程注浆抬升机理及效果研究[D].天津: 天津大学, 2016 ZHANG Xiaoshuang. Study on the mechanism and effect of grouting uplift in underground construction[D].Tianjin: Tianjin University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10056-1017131105.htm |
| [7] |
冯旭海.压密注浆作用机理与顶升效应关系的研究[D].北京: 煤炭科学研究总院, 2003 FENG Xuhai. A research on laws between lift-effect and the mechanism compaction grouting[D]. Beijing: China Coal Research Institute, 2003 http://cdmd.cnki.com.cn/Article/CDMD-83301-2004041295.htm |
| [8] |
侯艳娟, 张顶立, 陈峰宾. 隧道施工下穿建筑物注浆抬升机制及预测研究[J]. 岩石力学与工程学报, 2011, 30(12): 2407. HOU Yanjuan, ZHANG Dingli, CHEN Fengbin. Study of mechanism and prediction of grouting uplift in tunnel construction undercrossing buildings[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2407. |
| [9] |
郭乐, 杨新安, 吴东鹏. 高速铁路软土复合路基沉降注浆治理现场试验研究[J]. 中国铁道科学, 2015, 36(6): 1. GUO Le, YANG Xinan, WU Dongpeng, et al. Field test on treating settlement by grouting for soft soil composite subgrade of high speed railway[J]. China Railway Science, 2015, 36(6): 1. DOI:10.3969/j.issn.1001-4632.2015.06.01 |
| [10] |
逄铁铮.大断面城市隧道穿越复杂建筑物群的安全性控制研究[D].北京: 北京交通大学, 2015 PANG Tiezheng. Security control for large secton of urban tunnel through a complex group of buildings[D]. Beijing: Beijing Jiaotong University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611863.htm |
| [11] |
SHARGHI M, CHAKERI H, OZCELIK Y. Investigation into the effects of two component grout properties on surface settlements[J]. Tunnelling and Underground Space Technology, 2017, 63: 205. DOI:10.1016/j.tust.2017.01.004 |
| [12] |
OCHMANSKI M, MODONI G, BZOWKA J. Numerical analysis of tunnelling with jet-grouted canopy[J]. Soils & Foundations, 2015, 55(5): 929. DOI:10.1016/j.sandf.2015.08.002 |
| [13] |
NICOLINI E, NOVA R, NEGI A. Modelling of a tunnel excavation in a non-cohesive soil improved with cement mix injections[J]. Computers & Geotechnics, 2000, 27(4): 249. DOI:10.1016/s0266-352x(00)00003-3 |
| [14] |
SCHWEIGER H F. Numerical modelling of settlement compensation by means of fracture grouting[J]. Journal of the Japanese Geotechnical Society Soils & Foundation, 2004, 44(1): 71. DOI:10.3208/sandf.44.71 |
| [15] |
NI J C, CHENG W C. Monitoring and modeling grout efficiency of lifting structure in soft clay[J]. International Journal of Geomechanics, 2010, 10(6): 223. DOI:10.1061/(asce)gm.1943-5622.0000026 |
| [16] |
唐智伟, 赵成刚. 注浆抬升地层的机制、解析解及数值模拟分析[J]. 岩土力学, 2008, 29(6): 1512. TANG Zhiwei, ZHAO Chenggang. Mechanisms of ground heave by grouting and analytical solutions & numerical modeling[J]. Rock and Soil Mechanics, 2008, 29(6): 1512. DOI:10.16285/j.rsm.2008.06.032 |
| [17] |
张冬梅, 邹伟彪, 闫静雅. 软土盾构隧道横向大变形侧向注浆控制机理研究[J]. 岩土工程学报, 2014, 36(12): 2203. ZHANG Dongmei, ZOU Weibiao, YAN Jingya. Effective control of large transverse deformation of shield tunnels using grouting in soft deposits[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2203. DOI:10.11779/CJGE201412007 |
| [18] |
孙锋, 张顶立, 陈铁林, 等. 土体劈裂注浆过程的细观模拟研究[J]. 岩土工程学报, 2010, 32(3): 474. SUN Feng, ZHANG Dingli, CHEN Tielin, et al. Meso-mechanical simulation of fracture grouting in soil[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 474. |
| [19] |
YANG X L, WANG J M. Ground movement prediction for tunnels using simplified procedure[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2011, 26(3): 462. DOI:10.1016/j.tust.2011.01.002 |
| [20] |
LI W X, LI J F, WANG Q, et al. SMT-GP method of prediction for ground subsidence due to tunneling in mountainous areas[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2012, 32: 198. DOI:10.1016/j.tust.2012.06.012 |
| [21] |
施成华, 彭立敏, 刘宝琛. 浅埋隧道开挖对地表建筑物的影响[J]. 岩石力学与工程学报, 2004, 23(19): 3310. SHI Chenghua, PENG Limin, LIU Baochen. Influence of shallow tunnel excavation on ground surface buildings[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3310. DOI:10.3321/j.issn:1000-6915.2004.19.017 |
| [22] |
YUN J W, PARK J J, KWON Y S, et al. Cement-based fracture grouting phenomenon of weathered granite soil[J]. KSCE Journal of Civil Engineering, 2016, 21(1): 1. DOI:10.1007/s12205-016-0862-1 |
| [23] |
MARCHI M, GOTTARDI G, SOGA K. Fracturing pressure in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(2): 04013008. DOI:10.1061/(asce)gt.1943-5606.0001019 |
| [24] |
张连震, 李志鹏, 张庆松, 等. 基于土体非线性压密效应的劈裂注浆机制分析[J]. 岩石力学与工程学报, 2016, 35(7): 1483. ZHANG Lianzhen, LI Zhipeng, ZHANG Qingsong, et al. Split grouting mechanism based on nonlinear characteristics of compression process of soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1483. DOI:10.13722/j.cnki.jrme.2015.0565 |
 2019, Vol. 51
2019, Vol. 51


