2. 交通基础设施安全风险管理行业重点实验室(东南大学), 南京 210096;
3. 南京长江第三大桥有限责任公司, 南京 211808
2. Key Laboratory of Safety and Risk Management on Transport Infrastructures (Southeast University), Nanjing 210096, China;
3. Nanjing No.3 Yangtze River Bridge Ltd., Nanjing 211808, China
受大气温度、太阳辐射等因素的影响,桥梁结构的温度场随时间变化[1].温度引起的结构内力和变形是桥梁设计、施工和运营阶段的研究热点[2-4].准确掌握桥梁温度场的分布特点是研究结构温度效应的必要前提.
20世纪60年代,研究人员对混凝土梁的温度分布进行了研究[5-6].近年来,随着大跨钢结构桥梁的广泛应用和监测技术的发展,使得基于实测数据的大跨桥梁温度场分析成为可能.文献[7]基于3 a的温度监测数据,采用数理统计的方法,对钢箱梁有效温度和竖向温度梯度进行了研究,指出竖向温度梯度服从多折线分布.文献[8]利用润扬长江大桥的温度监测数据,对钢箱梁顶板横向温度梯度进行研究,结果表明扁平钢箱梁顶板的横向温度梯度明显.文献[9]基于润扬大桥钢箱梁的温度观测结果,研究了扁平钢箱梁内部温度的分布特点,但未与规范进行对比.文献[10]较全面地研究了扁平钢箱梁的温度分布,总结了钢箱梁顶板横向温度分布的3种模式.文献[11]研究了香港青马大桥的温度分布特点,并以此为基础对桥梁结构状态进行评估.由于温度测点的限制,目前对大跨桥梁温度场的研究主要集中在钢箱梁上,对其他构件温度特点的研究较少.但是,对大型缆索承重桥梁而言,挠度、索力等指标不仅受到钢箱梁温度场的影响,还会受塔梁温差、塔温度梯度等的影响.因此,有必要对大型桥梁主要构件(主梁、索塔等)的温度作用特征进行研究.
本文以南京长江三桥监测数据为基础,分析各主要构件温度随时间变化的规律;并考虑太阳辐射强度因素的影响,研究构件温度和大气温度的相关关系;随后分析各构件温度梯度的特点,并与现有国内外规范的相关规定进行比较分析;最后采用广义帕累托分布模型对100 a重现期的各温度作用极值进行估计.
1 南京长江三桥温度传感器布置南京长江三桥主桥是一座钢塔钢箱梁斜拉桥,其跨径布置为63 m+257 m+648 m+257 m+63 m.该桥于2005年10月份建成通车,次年监测系统投入使用.该监测系统的监测项目包括温度、索力、挠度、应力等.其中,温度监测子系统包括两种传感器:一种是美国R.M.YOUNG 41372型温湿度传感器(精度为±0.3 ℃,采样频率为10 Hz),用以监测大气温度;另一种是HBL型应变温度补偿片(精度:±0.5 ℃,每半小时测量一次),用于监测钢箱梁和索塔内部温度.
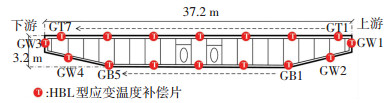
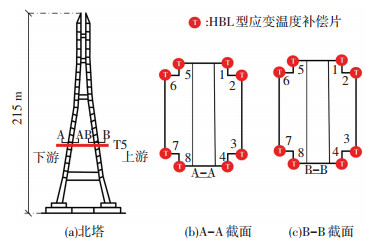
南京长江三桥采用扁平钢箱梁设计(梁高3.2 m,宽37.2 m).跨中截面温度传感器的布置形式如图 1所示.其中,钢箱梁顶板有7个测点(GT1~GT7);底板布置5个测点(GB1~GB5);两侧腹板各布置2个测点(GW1~GW4).南京长江三桥设计为弧线形钢索塔,塔高215 m.温度传感器在索塔内采用上下游对称布置,在箱室的4个角点各布置两个测点,编号为1~8.索塔T5截面温度传感器的布置情况如图 2所示.
|
图 1 钢箱梁跨中截面温度测点布置 Fig. 1 Layout of thermal sensors at mid-span section of the steel box girder |
|
图 2 索塔T5截面温度测点布置 Fig. 2 Layout of thermal sensors at T5 section of the tower |
根据南京长江三桥温度传感器的布置特点,分别选取钢箱梁和索塔为对象研究其温度随时间变化的规律.一般而言,温度沿钢箱梁纵向和索塔竖向的变化是忽略不计的[11-12].因此,分别选取钢箱梁跨中截面和索塔T5截面进行分析.
截面内的温度作用可分为温度梯度和有效温度.其中,温度梯度描述温度沿截面的分布特点,包括温差和分布形式;有效温度是截面温度的代表值,对于温度传感器均匀分布的匀质材料截面,有效温度即为各温度监测数据的平均值.
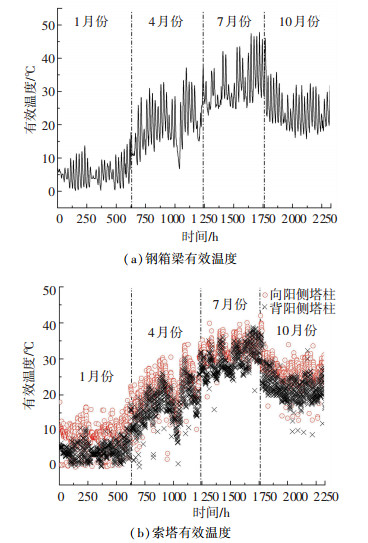
考虑温度作用的季节性特征,分别选取2007年1月份(冬季)、4月份(春季)、7月份(夏季)和10月份(秋季)的温度小时平均数据进行分析.钢箱梁有效温度具有显著的季节性特点,如图 3(a)所示.其中,实测有效温度的最大值为47.81 ℃,最小值为0.22 ℃.对于索塔而言,由于两个塔柱距离较近,向阳侧塔柱较背阳侧塔柱受太阳辐射影响大,两者的有效温度存在明显的差异.南京长江三桥纵桥向沿东南方向,桥塔上游为向阳侧、下游为背阳侧.索塔向阳侧和背阳侧的有效温度随季节的变化特点如图 3(b)所示,向阳侧有效温度的最大值为41.97 ℃,背阳侧为38.78 ℃;向阳侧有效温度的最小值为0 ℃,背阳侧为0.06 ℃.由图 3(b)可知,向阳侧和背阳侧塔柱的有效温度变化趋势一致,但是由于向阳侧塔柱受太阳直射,其有效温度普遍高于背阳侧.
|
图 3 钢箱梁和索塔温度随时间变化特点 Fig. 3 Variation law of the temperature of steel box girder and tower over time |
构件有效温度已被证明与大气温度存在很强的线性相关性,文献[10]利用一年的钢箱梁温度监测数据和大气温度监测数据进行回归分析,得到了大气温度和钢箱梁有效温度的线性回归关系.但构件温度除受大气温度的影响外,还受太阳辐射强度的影响.大气温度变化的速率在一定程度上能反映太阳辐射强度的变化规律.因此,以下将分析不同辐射条件下构件温度与大气温度的相关关系.
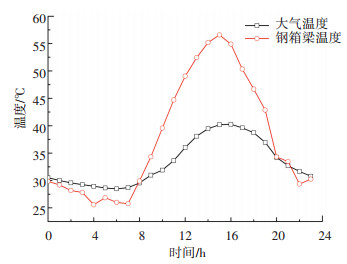
选取2007年7月26日的钢箱梁温度tG和大气温度tA进行分析,其日变化规律如图 4所示.钢箱梁和大气温度在无辐射条件下数值较为接近;由于钢箱梁材料的热辐射系数大,随着辐射强度的增强钢箱梁温度迅速上升导致其在数值上超过空气温度.虽然在辐射的影响下,钢箱梁温度和大气温度变化速率和幅值存在较大的差异,但两者总体的变化趋势是一致的,即温度均是随着辐射强度的增强而升高.
|
图 4 钢箱梁温度与大气温度的日变化规律 Fig. 4 Daily variation law of girder and ambient temperatures |
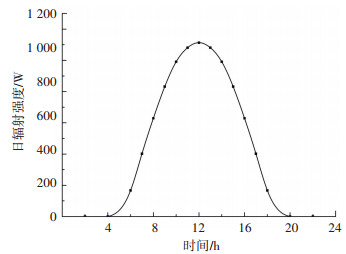
由于辐射强度受众多因素的影响,且某些因素的随机性高,难以准确模拟,但长期来看辐射强度的日变化规律是稳定的[13].根据南京长江三桥所处经纬度和《民用建筑供暖通风与空气调节设计规范》[14]的规定,南京三桥所在位置日辐射强度的变化规律如图 5所示.
|
图 5 日辐射强度变化规律 Fig. 5 Daily variation law of solar radiation intension |
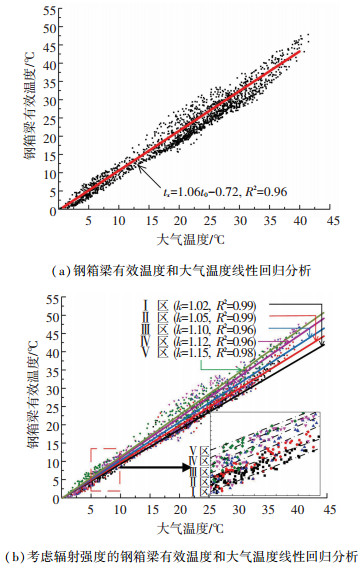
根据辐射强度的日变化规律,将一天24 h分为5个区间,分别对应辐射强度Ⅰ~Ⅴ.其中,Ⅰ级对应辐射强度0 W(对应时间轴0:00—4:00时,20:00—24:00时);Ⅱ级对应0~167 W(4:00—6:00时,18:00—20:00时);Ⅲ级对应167~629 W(6:00—8:00时,16:00—18:00时);Ⅳ级对应629~991.2 W(8:00—10:00时,14:00—16:00时);Ⅴ级对应991.2~1113.4 W(10:00—14:00时).假设同一辐射强度区间内辐射强度为定值,分别研究不同辐射强度下构件温度与大气温度的关系.以钢箱梁2007年1、4、7、10月份的监测数据为例,比较不同辐射强度下的钢箱梁有效温度与大气温度的相关关系,分析结果如图 6所示.不考虑辐射强度的影响,对监测数据进行线性拟合,分析结果如图 6(a)所示.根据辐射强度对温度数据进行分类,发现数据存在明显的分层现象,如图 6(b)所示.辐射强度低对应的钢箱梁有效温度位于底层,辐射强度高对应的数据位于上层.对不同辐射强度区间内的温度监测数据分别进行线性回归分析,分析结果如图 6(b)所示.随着辐射强度的提高,线性拟合公式中斜率参数k数值不断增大,由辐射强度Ⅰ对应的斜率1.02增加到辐射强度Ⅴ对应的1.15;且相关系数R均不小于不考虑辐射强度的相关系数.分析结果表明,辐射强度不会改变钢箱梁温度和大气温度的线性关系模式,但会引起斜率参数的变化.
|
图 6 钢箱梁有效温度和大气温度拟合分析结果 Fig. 6 Fitting results of effective temperature of steel box girder and ambient temperature |
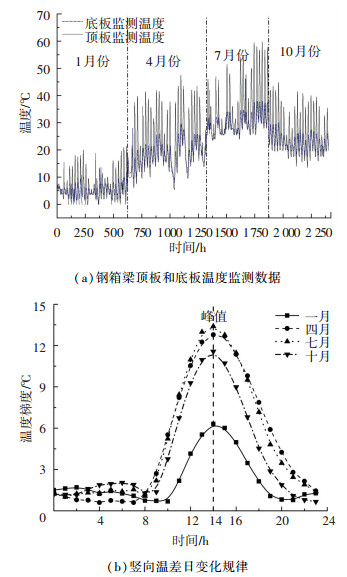
钢箱梁顶板受太阳直射,其温度相对底板要高,从而形成竖向温度梯度. 图 7(a)是钢箱梁上游侧顶板和底板4个月的温度监测数据,其中钢箱梁竖向温度差最大值出现在2007年7月26日的14:00—15:00时,最大温差为22.75 ℃. 图 7(b)是以月均值为代表值的钢箱梁竖向温度梯度的日变化规律.四季的竖向温差的日变化规律相似,即竖向温差在日出前保持较低水平,然后逐渐增大,直至14:00—15:00时达到峰值,最后随着日落不断减小.
|
图 7 钢箱梁竖向温度梯度分析 Fig. 7 Analysis of vertical temperature gradient of steel box girder |
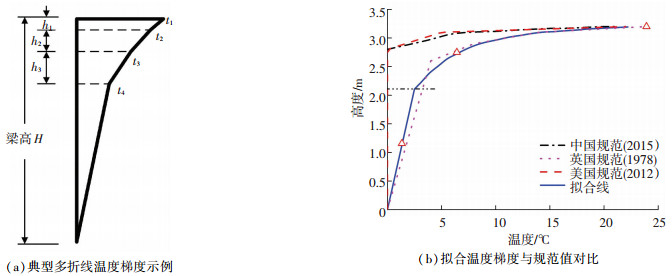
多折线模型常用于模拟钢箱梁竖向温度分布,如图 8(a)所示.中国JTG D60-2015[15]、英国BS 5400[16]、欧洲BS EN 1991-1-5[17]和美国LRFDUS-6[18]都对桥梁竖向温度梯度作了规定.其中,英国规范和欧洲规范对桥梁竖向温度梯度的规定一致;LRFDUS-6根据气候条件将全美分为4个区,每个区分别定义了竖向温度梯度数值.本文选取3区对应的竖向温度梯度进行分析,因为此区域的温度梯度与中国规范较为接近.基于最大竖向温差对应的顶板、腹板和底板的温度监测数据,参考中国铁路规范温度梯度的设置(即假设以腹板底部为界,上部是指数函数分布,下部是线性分布),经3个已知点拟合得到新的温度梯度线,如图 8(b)所示.由图 8(b)可知,相比中国和美国规范,实测钢箱梁竖向温度分布形式与英国规范BS 5400更为接近.
|
图 8 钢箱梁竖向温度梯度分布 Fig. 8 Vertical temperature gradient distribution form for steel box girder |
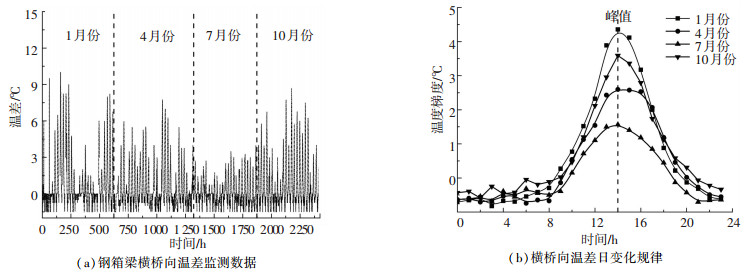
桥梁横向温度梯度在数值上一般远小于竖向温度梯度,但对于特殊桥梁(例如扁平钢箱梁桥),其横向温度梯度较大.例如,文献[19]通过连续监测数据统计分析发现Cleddau桥的横向温度差值达到了15 ℃.通过南京长江三桥的温度监测数据分析可知,底板最大横向温差为2.5 ℃,可忽略.下文以顶板温度监测数据为例进行横向温度梯度分析.由于钢箱梁横桥向温差主要受太阳辐射的影响,本文选取钢箱梁顶板上游侧(向阳侧)的温度传感器GT1和下游侧(背阳侧)的温度传感器GT7的差值,即(tGT1-tGT7),作为横桥向温差进行研究.根据监测数据(图 9(a))可知,钢箱梁横桥向温差在冬季更为显著,顶板的最大横向温度梯度出现在冬季(2007年1月7日14:00—15:00时),最大温差为10 ℃.钢箱梁顶板横向温度梯度对辐射角度较为敏感,冬季太阳辐射角低,导致横桥向温差大. 图 9(b)是以月均值为代表值的钢箱梁横向温度梯度的日变化规律.由图 9(b)可知,四季的横向温差的日变化具有相似的规律,即横向温差在日出前保持较小数值,然后逐渐增大,直至14:00—15:00时达到峰值,最后随着日落不断减小.
|
图 9 钢箱梁顶板横桥向温度梯度分析 Fig. 9 Analysis of transverse temperature gradient of deck of steel box girder |
以顶板横向温差最大值对应时刻(2007年1月7日14:00—15:00时)的数据为基础,分析钢箱梁顶板横向温度的分布形式,研究结果如图 10所示.顶板横桥向温度梯度适用多折线模型.其中GT1和GT7之间的温差是太阳辐射引起的;GT2和GT6位置处温度较高是因为该处位于重车道位置,由于轮胎与桥面的摩擦产生热量导致顶板温度升高[8];GT4处温度处于低值点是因为该处位于中央分隔带,分隔带材料的吸热能力弱于铺装层,且无行车摩擦产生的热量.

|
图 10 钢箱梁顶板横桥向温度梯度分布形式 Fig. 10 Transverse temperature gradient distribution form for the deck plate of steel box girder |
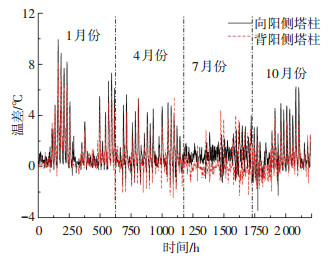
由于同墩的上下游塔柱受太阳辐射的影响不同,分别分析向阳侧和背阳侧塔柱的截面温度分布情况.上游侧塔柱截面温差定义为塔柱外侧温度监测值与内侧之差,下游塔柱类似.上游侧和下游侧塔柱截面温差的监测数据如图 11所示.塔柱截面温度梯度与钢箱梁横桥向温差类似,在冬季温差更显著.塔柱的最大温差出现在冬季,数值为9.94 ℃,时间是2007年1月7日的16:00—17:00时.向阳侧塔柱由于受太阳辐射的影响大,其截面正温度梯度明显高于背阳侧塔柱.以塔柱温度梯度的月均值为代表值分析其日变化规律,分析结果如图 12所示.向阳侧塔柱截面温差受太阳辐射影响显著,在日出前温差保持较稳定水平,随着辐射强度的增强,温差达到峰值,最后随着日落温差逐渐减小.背阳侧塔柱温差具有类似的规律,但受太阳辐射的影响不明显,表现为数据更离散.由于温度传感器只在塔柱角点布置,无法分析塔柱温差的分布形式,可假设塔柱温度沿截面线性分布.
|
图 11 塔柱截面温差监测数据 Fig. 11 Recorded temperature difference along the tower section |

|
图 12 塔柱截面温差日变化规律 Fig. 12 Daily variation law of temperature difference of tower |
由于经典的区组模型不能充分利用数据中包含的极值信息,本文采用极值理论中的广义帕累托分布模型进行温度荷载的极值预测.广义帕累托分布是对超过一定阈值后的尾部数据进行拟合的函数,如果随机变量X(x∈D(σ, ξ))的分布函数为
| $ G(x;\xi , \sigma ) = \left\{ {\begin{array}{*{20}{l}} {1 - {{\left( {1 + \xi \frac{x}{\sigma }} \right)}^{ - \frac{1}{\xi }}}, }&{\xi \ne 0;}\\ {1 - \exp \left( { - \frac{x}{\sigma }} \right), }&{\xi = 0.} \end{array}} \right. $ | (1) |
则称X服从广义帕累托分布.
其中:
| $ D(\sigma , \xi ) = \left\{ {\begin{array}{*{20}{l}} {[0, + \propto ), }&{\xi \ge 0;}\\ {\left[ {\mu , \mu - \frac{\sigma }{\xi }} \right], }&{\xi < 0.} \end{array}} \right. $ | (2) |
式中ξ为形状参数,σ为尺度参数.
采用广义帕累托分布估计温度作用极值的具体步骤:1)阈值选取.采用广义帕累托分布拟合超出量时,合理选择阈值u是一个关键问题.阈值大,超出样本数量少,估计量的方差大;阈值小,超出量与广义帕累托分布相差较大,估计量成为有偏估计.广义帕累托分布的平均超出量函数e(u)是u的线性函数,对于给定的样本X1, X2, …, Xn,大于阈值的样本平均超出量函数应该在一条直线附近波动.在选取阈值取值时,可以通过关注某个阈值u0以后e(u)的斜率变化特点来确定阈值取值,如果斜率保持不变,这个点通常可以作为阈值点. 2)参数估计.根据既有的样本数据,对广义帕累托分布模型的参数进行估计,常见的估计方法有极大似然估计、概率权矩估计、L矩法等. 3)重现水平.所谓T年重现水平u(T)就是要求在T年时间内,超过阈值u(T)的平均次数为1.在重现期T确定之后,重现水平即为p分位(p = 1-1/T)对应的分位数xp,分位数xp的估计[20]为
| $ {x_p} = {u_0} + \frac{{\hat \sigma }}{{\hat \xi }}\left[ {{{\left( {\frac{n}{{{N_u}}}(1 - p)} \right)}^{ - \hat \xi }} - 1} \right], $ | (3) |
其中
以钢箱梁纵向温度梯度小时平均数据为例(样本总量n=2 424),采用广义帕累托分布模型进行极值估计.
图 13是平均超出量函数值与对应阈值的关系图,当阈值取大于5时,平均超出量函数与阈值取值呈线性关系,故本文阈值取为5.利用MATLAB平台,采用极大似然估计,在95%的置信度水平下,计算得到形状参数估计值

|
图 13 钢箱梁竖向温度梯度平均超出量 Fig. 13 Mean exceedance plot for vertical temperature gradient of steel box girder |
按照估计钢箱梁竖向温度梯度的方法,分别对最大塔梁温差、钢箱梁横向温差和索塔温差进行100 a重现期的极值估计,估计结果与各国规范的对比结果见表 1.
| 表 1 极值估计结果与各国规范规定对比 Tab. 1 Comparison of estimation of extreme values and existing codes of various nations |
钢箱梁竖向温度梯度的极值估计结果大于中国规范的规定值,接近英国规范的规定值;钢箱梁横向温度梯度的极值估计大于中国规范的规定值,主要由于南京长江三桥采用的是扁平钢箱梁设计;索塔温度梯度的极值估计远大于中国规范的规定值,主要因为南京长江三桥采用钢索塔设计,而规范中的规定主要针对混凝土索塔;虽然设计规范中未考虑塔梁温差的影响,但本文的塔梁温差估计值较大,不可轻易忽视.鉴于南京长江三桥钢索塔的设计特点,本文给出的温度作用估计值对钢箱梁斜拉桥温度效应的分析具有一定的参考价值,同时也为桥梁设计规范修编提供一定的实测数据支撑.
5 结论1) 考虑太阳辐射强度的基础上,得到不同辐射强度条件下对应的钢箱梁有效温度与大气温度的相关关系.相比于不考虑辐射强度的情况,提出了对钢箱梁有效温度和大气温度之间关系的刻画更为细致的方法.
2) 南京长江三桥钢箱梁竖向温度梯度的最大值出现在夏季,其分布形式与英国规范BS 5400中的规定更为接近.钢箱梁顶板横向温差最大值出现在冬季,数值为10 ℃,与竖向温度梯度处于同一量级.
3) 基于南京三桥钢箱梁和钢索塔的温度监测数据,采用帕累托分布模型对温度作用进行100 a重现期的极值预测.除钢箱梁竖向温度梯度的极值估计接近BS 5400的规定外,其他温度作用极值估计的结果均大于规范规定.对钢箱梁斜拉桥温度效应的分析具有一定的参考价值,同时也为桥梁设计规范修编提供一定的数据支撑.
| [1] |
ZUK W. Thermal behavior of composite bridges-insulated and uninsulated[J]. Highway Research Record, 1965(76): 231. |
| [2] |
任远, 刘小玲, 黄侨. 斜拉桥恒载索力长期变化趋势分析与评估[J]. 哈尔滨工业大学学报, 2015, 47(6): 103. REN Yuan, LIU Xiaoling, HUANG Qiao. The long-term trend analysis and assessment of the cable forces due to dead load in cable-stayed bridges[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 103. DOI:10.11918/j.issn.0367-6234.2015.06.019 |
| [3] |
邓小伟, 石雪飞, 阮欣. 超大跨径钢斜拉桥的温度作用调研与温度效应分析[J]. 石家庄铁道大学学报(自然科学版), 2010, 23(3): 57. DENG Xiaowei, SHI Xuefei, RUAN Xin. Investigation and analysis of temperature acts on long-span steel cable-stayed bridges[J]. Journal of Shijiazhuang Railway Institute (Natural Science Edition), 2010, 23(3): 57. DOI:10.3969/j.issn.2095-0373.2010.03.012 |
| [4] |
刘来君. 大跨径桥梁施工控制温度荷载[J]. 长安大学学报(自然科学版), 2003, 23(2): 61. LIU Laijun. Temperature load of construction controlling for long-span bridge[J]. Journal of Changan University (Natural Science Edition), 2003, 23(2): 61. DOI:10.3321/j.issn:1671-8879.2003.02.015 |
| [5] |
叶见曙, 贾琳, 钱培舒. 混凝土箱梁温度分布观测与研究[J]. 东南大学学报(自然科学版), 2002, 32(5): 788. YE Jianshu, JIA Lin, QIAN Peishu. Observation and research on temperature distribution in concrete box girders[J]. Southeast University (Natural Science Edition), 2002, 32(5): 788. DOI:10.3321/j.issn:1001-0505.2002.05.024 |
| [6] |
LUCAS J M, VIRLOGEUX M, LOUIS C. Temperature in the box girder of the Normandy Bridge[J]. Structural Engineering International, 2005, 15(3): 156. DOI:10.2749/101686605777963044 |
| [7] |
LUCASJ M, BERRED A, LOUIS C. Thermal actions on a steel box girder bridge[J]. Structures & Buildings, 2003, 156(2): 175-182. DOI:10.1680/stub.2003.156.2.175 |
| [8] |
DING Y, ZHOU G, LI A, et al. Thermal field characteristic analysis of steel box girder based on long-term measurement data[J]. International Journal of Steel Structures, 2012, 12(2): 219. DOI:10.1007/s13296-012-2006-x |
| [9] |
孙君, 李爱群, 丁幼亮. 润扬长江大桥钢箱梁的温度分布监测与分析[J]. 公路交通科技, 2009, 26(8): 94. SUN Jun, LI Aiqun, DING Youliang. Observation and research on temperature distribution in steel box girder of Runyang Yangtze River Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(8): 94. DOI:10.3969/j.issn.1002-0268.2009.08.019 |
| [10] |
DENG Y, LI A, LIU Y, et al. Investigation of temperature actions on flat steel box girders of long-span bridges with temperature monitoring data[J]. Advances in Structural Engineering, 2018, 21(14): 2099. DOI:10.1177/1369433218766946 |
| [11] |
XIA Y, CHEN B, ZHOU X, et al. Field monitoring and numerical analysis of Tsing Ma Suspension Bridge temperature behavior[J]. Structural Control and Health Monitoring, 2013, 20(4): 560. DOI:10.1002/stc.515 |
| [12] |
LIU Y, QIAN Z, HU H. Thermal field characteristic analysis of steel bridge deck during high-temperature asphalt pavement paving[J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2811. DOI:10.1007/s12205-016-0027-2 |
| [13] |
WESTGATE R, KOO K Y, BROWNJOHN J. Effect of solar radiation on suspension bridge performance[J]. Journal of Bridge Engineering, 2014, 20(5): 04014077. DOI:10.1061/(ASCE)BE.1943-5592.0000668 |
| [14] |
中国建筑科学研究院.民用建筑供暖通风与空气调节设计规范: GB 50736—2012[S].北京: 中国建筑工业出版社, 2012 China Academy of Building Research.Design code for heating ventilation and air conditioning of civil buildings: GB 50736—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [15] |
中交公路规划设计院.公路桥涵设计通用规范: JTG D60—2015[S].北京: 人民交通出版社, 2015 CCCC HighwayConsultants. General code for design of highway bridges and culverts: JTG D60—2015[S]. Beijing: China Communications Press, 2015 |
| [16] |
British Standards Institution. Steel, concrete and composite bridges: specification for loads: BS 5400[S]. London: British Standards Institution, 1978
|
| [17] |
British Standards Institution. Eurocode 1: actions on structures part 1-5: General actions—thermal actions: BS EN 1991-1-5[S].London: British Standards Institution, 2003
|
| [18] |
American Association of State Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. 6th ed. Washington DC: American Association of State Highway and Transportation Officials, 2012
|
| [19] |
KROMANIS R, KRIPAKARAN P. Predicting thermal response of bridges using regression models derived from measurement histories[J]. Computers & Structures, 2014, 136: 64. DOI:10.1016/j.compstruc.2014.01.026 |
| [20] |
HOLMES J, MORIARTY W. Application of the generalized Pareto distribution to extreme value analysis in wind engineering[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1999, 83(1/2/3): 1. DOI:10.1016/S0167-6105(99)00056-2 |
 2019, Vol. 51
2019, Vol. 51


