2. 北京宇航系统工程研究所, 北京 100076
2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China
空中战争的目标正逐渐变为高空、高速、大机动、具有智能逃逸和隐身技术的新型飞行器,这些空中目标以及随之出现的新空战模式对空空导弹的性能,特别是对导弹的响应速度提出了更高的要求.在这种形势下,传统的气动力控制方案很难满足空空导弹的发展需求,新的复合控制技术应运而生,与一般的防空导弹的直接力装置不同,适用于空空导弹的直接力装置有其特殊性.受到空空导弹体积的严格限制,发动机引流直接力装置更加适用于空空导弹,这种直接力装置由分别安装在弹体尾部的6组或4组引流阀门组成[1-2],当阀门打开时,主发动机的燃气被引流至弹体侧向喷出,形成直接力控制弹体姿态变化.
针对直接力与气动力复合控制系统的设计问题,国内外学者提出了多种直接力/气动力复合控制方法.目前,常用的直接力/气动力复合控制策略主要有基于指令分配[3]、控制分配[4]和直接力与气动力联合设计[5]3种类型.文献[6]采用指令分配和变结构控制将力和力矩设计有机结合,取得了良好的跟踪效果.文献[7]考虑执行机构特性和外界干扰的影响,基于反步法设计导弹直接力与气动力复合控制律.文献[8]针对直接力/气动力复合控制中连续、离散并存的特点使用SDRE方法完成复合控制系统设计,并进行了稳定性分析.文献[9]采用传统方法设计各子系统控制律,用模糊逻辑实现复合控制.文献[10]将直接力假设为连续控制量,采用经典三回路设计方法设计俯仰/偏航复合控制器.文献[11]设计了常规气动力控制和模糊逻辑直接力控制的导弹复合控制系统,可实现对导弹气动力和直接力的协调使用.文献[12]考虑侧喷干扰作用,设计了一种基于模型参考自适应的自动驾驶仪.文献[13]采用反馈加前馈控制机构设计导弹复合控制系统,并采用进化算法对复合控制系统参数进行多目标优化.文献[14]将气动力和直接力分别设计为滑模控制中的等效控制和切换控制,采用分段滑模控制思想设计复合控制系统.文献[15]针对参数的不确定性和外界扰动,基于广义预测控制和自适应终端滑模控制方法设计姿态控制系统.尽管上述几种复合控制方法可以在一定程度上取得了良好的收敛速率和控制精度,但是指令跟踪误差的收敛时间不能精确估计,对于期望收敛特性,缺少系统参数选择方法.固定时间收敛控制方法不需要知道系统初值状态信息,能保守估计系统的收敛时间,所以对空空导弹直接力/气动力复合控制固定时间收敛问题的研究是很有必要的.
本文研究末制导阶段空空导弹直接力/气动力复合控制系统固定时间收敛问题.为了便于说明控制系统的设计过程,考虑导弹在俯仰平面内的过载控制系统,首先建立了过载复合控制系统的数学模型,对数学模型进行分析,得到了用于控制律设计的简化模型.然后基于固定时间收敛的滑模控制方法和动态控制分配技术设计了复合控制策略.最后进行仿真验证,结果表明所设计的复合控制系统在保证固定时间内快速建立过载的同时,可实现对直接力和气动力的协调使用.
1 直接力/气动力复合控制系统数学模型 1.1 弹体纵向动力学模型针对静稳定的轴对称导弹,采用如图 1所示的位于导弹尾部6喷口发动机引流直接力装置. 图 1中,黑色模块表示直接力喷口; Ox1y1z1表示弹体坐标系,坐标系的原点O取在导弹的质心上,Ox1轴与弹体纵轴重合,指向头部为正,Oy1轴位于弹体纵向对称面内与Ox1轴垂直,指向上为正,Oz1轴垂直于Ox1y1平面,方向按右手直角坐标系确定[16].对于正常式导弹,在弹体坐标系中,导弹升降舵的后缘向下,舵偏角δe为正(即升降舵后缘往下),将引起负的俯仰力矩,使导弹建立负攻角,产生负过载.直接力作用效果刚好与之相同,正直接力使导弹低头,建立负攻角,产生负过载.

|
图 1 复合控制空空导弹及直接力装置示意图 Fig. 1 Structure of the air-to-air missile with blended control |
由于直接力一般用在制导末端以提高导弹的控制精度和响应速度,为了便于说明复合控制系统的设计过程,只考虑末制导阶段导弹在纵向平面的运动.在末制导阶段可以将导弹的飞行速度和飞行高度视为常值.假设导弹为理想刚体,质心位置不变,质量不变,导弹的姿态运动数学模型[17]分别为
| $ \dot \alpha = {\omega _z} - {b_\alpha }\alpha - {b_{{\delta _e}}}{\delta _e} - b_{{\delta _e}}^\prime {f_y}, $ | (1) |
| $ {{\dot \omega }_z} = - {a_\alpha }\alpha - {a_{{\omega _z}}}{\omega _z} - {a_{{\delta _e}}}{\delta _e} - a_{{\delta _e}}^\prime {f_y}, $ | (2) |
| $ {n_y} = \frac{V}{g}\left( {{\omega _z} - \dot \alpha } \right). $ | (3) |
其中:α为导弹攻角,ωz为俯仰角速率,ny为导弹过载,δe为升降舵偏角,fy为直接力,g为重力加速度; aα, aωz, aδe, a′δe, bα, bδe, b′δe为动力学系数; Jz为转动惯量,L为侧喷发动机到质心的距离,m为导弹质量,V为导弹速度.
设虚拟控制输入ν为控制力矩
| $ v = \mathit{\boldsymbol{Wu}}, $ | (4) |
式中
对于正常布局的导弹,由于升降舵面和直接力装置产生的控制力对
| $ \dot \alpha = {\omega _z} - {b_\alpha }\alpha , $ | (5) |
| $ {{\dot \omega }_z} = - {a_\alpha }\alpha - {a_{{\omega _z}}}{\omega _z} + {a_j}\nu . $ | (6) |
如果选取x=[x1, x2]T=[ny,
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - \frac{1}{{T_m^2}}{x_1} - 2\frac{{{\xi _m}}}{{{T_m}}}{x_2} + \frac{{V \cdot {K_m}}}{{g \cdot T_m^2}}\nu . \end{array} \right. $ | (7) |
式中:
升降舵数学模型[18]用二阶系统描述为
| $ {\delta _e} = \frac{{\omega _\delta ^2}}{{{s^2} + 2\xi {\omega _\delta }s + \omega _\delta ^2}}{\delta _{ec}}, $ | (8) |
直接力装置数学模型[18]的一阶系统描述为
| $ {f_y} = \frac{1}{{\tau s + 1}}{f_{yc}}. $ | (9) |
式中:
引理1[19] 考虑如下系统
| $ \dot y = - a{y^{\frac{m}{n}}} - b{y^{\frac{p}{q}}},y\left( 0 \right) = {y_0}, $ | (10) |
其中a>0,b>0,m,n,p,q为正奇数且满足m>n,p<q.系统(10)全局固定时间稳定,调整时间Tf有界,满足
| $ {T_f} < {T_{\max }} = \frac{1}{a}\frac{n}{{m - n}} + \frac{1}{b}\frac{q}{{q - p}}. $ | (11) |
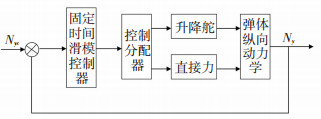
直接力/气动力复合控制的主要目的是实现对过载快速精确跟踪.复合控制系统结构如图 2所示.设计固定时间收敛滑模控制器,得到期望的控制力矩; 然后将其作为虚拟控制输入,使用动态控制分配技术将虚拟控制输入分别映射到升降舵和直接力装置操纵导弹改变姿态,快速建立过载.
|
图 2 复合控制系统 Fig. 2 The blended control system |
定义过载跟踪误差e=[e1, e2]T,其中e1=ny-nyc,e2=
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot e}_1} = {e_2},}\\ {{{\dot e}_2} = - \frac{1}{{T_m^2}}{n_y} - 2\frac{{{\xi _m}}}{{{T_m}}}{{\dot n}_y} + \frac{{V \cdot {K_m}}}{{g \cdot T_m^2}}\nu - {{\ddot n}_{yc}}.} \end{array}} \right. $ | (12) |
设计滑模面为
| $ s = {{\dot e}_1} + ae_1^{\frac{m}{n}} + be_1^{\frac{p}{q}}, $ | (13) |
式中:a,b为正常数; m,n,p,q为正奇数,且满足m>n,p<q.
在式(13)所示的滑模面的基础上,设计滑模控制律为
| $ \begin{array}{*{20}{c}} {\nu = \frac{{gT_m^2}}{{V{K_m}}}\left[ {\frac{1}{{T_m^2}}{n_y} + 2\frac{{{\xi _m}}}{{{T_m}}}{{\dot n}_y} + {{\dot n}_{yc}} - {e_2}\left( {a\frac{m}{n}e_1^{\frac{m}{n} - 1} + } \right.} \right.}\\ {\left. {\left. {b\frac{p}{q}e_1^{\frac{p}{q} - 1}} \right) - \frac{{{a_1}}}{{\sqrt 2 }}{{\left( {\frac{s}{{\sqrt 2 }}} \right)}^{\frac{{2n}}{n} - 1}} - \frac{{{b_1}}}{{\sqrt 2 }}{{\left( {\frac{s}{{\sqrt 2 }}} \right)}^{\frac{{2p}}{q} - 1}} - \eta {\rm{sgn}}\left( s \right)} \right].} \end{array} $ | (14) |
式中:η>0,a1>0,b1>0.
定理1 对于控制系统(12),当采用滑模面(13)及滑模控制律(14)时,有以下结论成立:1)s=0,∀t≥tf1成立,即滑模面s固定时间内收敛至0;2)e1=0,∀t≥tf2成立,即过载跟踪误差e1固定时间内收敛至0. 3)
证明 选取如下Lyapunov函数
| $ {V_1} = \frac{1}{2}{s^2}, $ | (15) |
对其进行求导得到
| $ \begin{array}{*{20}{c}} {{{\dot V}_1} = s\dot s = s\left[ { - \frac{1}{{T_m^2}}{n_y} - 2\frac{{{\xi _m}}}{{{T_m}}}{{\dot n}_y} + \frac{{V \cdot {K_m}}}{{g \cdot T_m^2}}\nu - {{\ddot n}_{yc}} + } \right.}\\ {\left. {{e_2}\left( {a\frac{m}{n}e_1^{\frac{m}{n} - 1} + b\frac{p}{q}e_1^{\frac{p}{q} - 1}} \right)} \right].} \end{array} $ | (16) |
将跟踪控制律(14)代入式(16),可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_1} = - s\frac{{{a_1}}}{{\sqrt 2 }}{{\left( {\frac{s}{{\sqrt 2 }}} \right)}^{\frac{{2m}}{n} - 1}} - s\frac{{{b_1}}}{{\sqrt 2 }}{{\left( {\frac{s}{{\sqrt 2 }}} \right)}^{\frac{{2p}}{q} - 1}} - \eta \cdot s \cdot {\rm{sgn}}\left( s \right) = }\\ { - {a_1}V_1^{\frac{m}{n}} - {b_1}V_i^{\frac{p}{q}} - \eta \left| s \right| \le - {a_1}V_1^{\frac{m}{n}} - {b_1}V_1^{\frac{p}{q}}.} \end{array} $ | (17) |
根据引理1,在式(14)所示的滑模控制律ν的作用下,V1=0,∀t≥tf1成立.进而可由Lyapunov函数(15)知s=0,∀t≥tf1成立,即滑模面s固定时间内收敛至0,且收敛时间满足
| $ {t_{f1}} < {T_{1\max }} = \frac{1}{{{a_1}}}\frac{n}{{m - n}} + \frac{1}{{{b_1}}}\frac{q}{{q - p}}, $ | (18) |
由s=0进一步得
| $ {{\dot e}_1} = - ae_1^{\frac{m}{n}} - be_1^{\frac{p}{q}}, $ | (19) |
根据引理1,e1=0,∀t≥tf2成立,即过载跟踪误差在固定时间内收敛至0,且收敛时间满足
| $ {t_{f2}} < {T_{2\max }} = \frac{1}{a}\frac{n}{{m - n}} + \frac{1}{b}\frac{q}{{q - p}}, $ | (20) |
根据滑模面(13)可得,当s=0,e1=0时,
综上,采用滑模面(13)及滑模控制律(14)时,复合控制系统(12)固定时间Tmax内收敛,且收敛时间Tmax满足
| $ \begin{array}{l} {T_{\max }} < {T_{1\max }} + {T_{2\max }} = \frac{1}{{{a_1}}}\frac{n}{{m - n}} + \frac{1}{{{b_1}}}\frac{q}{{q - p}} + \\ \;\;\;\;\;\frac{1}{a}\frac{n}{{m - n}} + \frac{1}{b}\frac{q}{{q - p}}. \end{array} $ | (21) |
空空导弹上具有特性完全不同的两套执行机构,直接力和气动力都能控制导弹的姿态运动.对于复合控制导弹,两个执行机构产生的控制效果存在严重的相互“斗争”情况,为协调使用直接力和气动力,一般采用控制分配的方法来实现.在传统控制分配中,通常假设执行器动态响应过程比系统动态快很多,从而将其忽略,这将降低控制分配精度,从而影响整个控制系统的性能.本文在控制分配过程中,额外考虑执行器动态响应过程,以得到更精确的分配解.考虑执行器位置限制和速率约束为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_{\min }} \le u\left( t \right) \le {\mathit{\boldsymbol{u}}_{\max }},}\\ {{\mathit{\boldsymbol{\rho }}_{\min }} \le \dot u\left( t \right) \le {\mathit{\boldsymbol{\rho }}_{\max }}.} \end{array}} \right. $ | (22) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\rho }}_{\min }} = {{\left[ {{{\underline {\dot \delta } }_e},{{\underline {\dot f} }_y}} \right]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{\rho }}_{\max }} = {{\left[ {\begin{array}{*{20}{c}} {{{\overline {\dot \delta } }_e}}&{{{\overline {\dot f} }_y}} \end{array}} \right]}^{\rm{T}}}.} \end{array}} \right. $ |
控制分配系统是一个数字控制系统,假设采样时间为T,则
| $ \dot u\left( t \right) \approx \frac{{u\left( t \right) - u\left( {t - T} \right)}}{T}. $ | (23) |
由式(22)、(23)可得升降舵和直接力的组合约束条件为
| $ \left\{ {\begin{array}{*{20}{l}} {\underline u \le u\left( t \right) \le \bar u,}\\ {\underline u \left( t \right) = \max \left\{ {{u_{\min }},{\rho _{\min }}T + u\left( {t - T} \right)} \right\},}\\ {\bar u\left( t \right) = \min \left\{ {{u_{\max }},{\rho _{\max }}T + u\left( {t - T} \right)} \right\}.} \end{array}} \right. $ | (24) |
采用基于二次规划的控制分配策略[20]:
| $ \left\{ \begin{array}{l} J = \mathop {\min }\limits_{u\left( t \right) \in K} \left\{ {{{\left\| {{W_1}\left[ {u(t) - {u_s}(t)} \right]} \right\|}^2} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left\| {{W_2}\left[ {u(t) - u(t - T)} \right]} \right\|}^2}} \right\},\\ K = \arg \mathop {\min }\limits_{\underline u \left( t \right) \le \left. {u(t)} \right) \le \bar u(t)} \left\| {{W_v}\left[ {Wu\left( t \right) - {u_s}\left( t \right)} \right]} \right\|. \end{array} \right. $ | (25) |
式中:W∈Rn×m(n)≤m)为控制效率矩阵,n表示虚拟控制量个数,m表示实际执行机构个数. u∈Rm为实际控制量,us∈Rm为期望的稳态控制量. W1,W2是权重矩阵,为对称矩阵,通常情况下,加权阵W1,W2依据操纵性能选取的,W1权值影响稳态控制量,权值的选择直接影响稳态下控制分配比例,根据操纵面操纵效率进行选择; W2则影响动态分配过程,可根据操纵面最大偏转速率进行选择.
根据式(1)、(2)可以得到系统的平衡状态
| $ {\alpha _e} = - \frac{{{a_{\delta e}} + {b_{\delta e}}{a_{wz}}}}{{{a_\alpha } + {a_{wz}}{b_\alpha }}}{\delta _{ze}} - \frac{{a_{\delta e}^\prime + b_{\delta e}^\prime {a_{wz}}}}{{{a_\alpha } + {a_{wz}}{b_\alpha }}}{f_{ye}}, $ | (26) |
| $ {w_{ze}} = - \frac{{{a_\alpha }{b_{\delta e}} - {a_{\delta e}}{b_\alpha }}}{{{a_\alpha } + {a_{wz}}{b_\alpha }}}{\delta _{ze}} + \frac{{{a_\alpha }b_{\delta e}^\prime - a_{\delta e}^\prime {b_\alpha }}}{{{a_\alpha } + {a_{wz}}{b_\alpha }}}{f_{ye}}. $ | (27) |
将式(26)、(27)代入式(3)中,可得
| $ {N_{yc}} = \frac{{V\left( {{a_\alpha }{b_{\delta e}} - {a_{\delta e}}{b_\alpha }} \right)}}{{g\left( {{a_\alpha } + {a_{wz}}{b_\alpha }} \right)}}{\delta _{ze}} + \frac{{V\left( {{a_\alpha }b_{\delta e}^\prime - a_{\delta e}^\prime {b_\alpha }} \right)}}{{g\left( {{a_\alpha } + {a_{wz}}{b_\alpha }} \right)}}{f_{ye}}. $ | (28) |
期望稳态时刻直接力为0,即fye=0,可得
| $ {\delta _{ze}} = \frac{{g\left( {{a_\alpha } + {a_{wz}}{b_\alpha }} \right)}}{{V\left( {{a_\alpha }{b_{\delta e}} - {a_{\delta e}}{b_\alpha }} \right)}}{N_{yc}}, $ | (29) |
即
| $ {u_s} = \left[ {\begin{array}{*{20}{c}} {\frac{{g\left( {{a_\alpha } + {a_{wz}}{b_\alpha }} \right)}}{{V\left( {{a_\alpha }{b_{\delta e}} - {a_{\delta e}}{b_\alpha }} \right)}}{N_{yc}}}\\ 0 \end{array}} \right]. $ | (30) |
非饱和情况下式(25)可简化为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{u\left( t \right)} \left\{ {{{\left\| {{\mathit{\boldsymbol{W}}_1}\left[ {u(t) - {u_s}(t)} \right]} \right\|}^2} + \left\| {{\mathit{\boldsymbol{W}}_2}[u(t) - } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left. {u(t - T)]} \right\|}^2}} \right\},\\ \mathit{\boldsymbol{Wu}}\left( t \right) = \nu \left( t \right). \end{array} \right. $ | (31) |
假设1 权重矩阵W1和W2是对称矩阵,并且
| $ u(t) = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{u}}_s}(t) + \mathit{\boldsymbol{F}}u(t - T) + \mathit{\boldsymbol{G}}\nu (t). $ | (32) |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{E}} = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{GW}}} \right)\mathit{\boldsymbol{W}}_3^{ - 2}\mathit{\boldsymbol{W}}_1^2,\mathit{\boldsymbol{F}} = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{GW}}} \right)\mathit{\boldsymbol{W}}_3^{ - 2}\mathit{\boldsymbol{W}}_2^2,\mathit{\boldsymbol{G}} = \\ \mathit{\boldsymbol{W}}_3^{ - 1}{\left( {\mathit{\boldsymbol{WW}}_3^{ - 1}} \right)^ + },{\mathit{\boldsymbol{W}}_3} = {\left( {\mathit{\boldsymbol{W}}_1^2 + \mathit{\boldsymbol{W}}_2^2} \right)^{\frac{1}{2}}}. \end{array} $ |
证明 当假设1成立时,‖W1[u(t)-us(t)]‖2+‖W2[u(t)-u(t-T)]‖2和‖W3[u(t)-u0(t)]‖有相同的最小值,式中W3=
加入线性约束Wu(t)=ν(t),权重矩阵W满秩,则加权广义逆的解为u(t)=(I-GW)u0(t)+Gν(t),式中G=W3-1(WW3-1)+,由此可得
| $ \begin{array}{l} u\left( t \right) = \underbrace {\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{GW}}} \right)\mathit{\boldsymbol{W}}_3^{ - 2}\mathit{\boldsymbol{W}}_1^2}_E{u_s}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\underbrace {\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{GW}}} \right)\mathit{\boldsymbol{W}}_3^{ - 2}\mathit{\boldsymbol{W}}_2^2}_Fu\left( {t - T} \right) + \mathit{\boldsymbol{G}}v\left( t \right). \end{array} $ |
至此可以通过求解约束二次型规划问题来得到最优的控制分配解.
3 仿真分析在25g过载指令下,验证所设计复合控制系统的跟踪效果.选择某型空空导弹在某高度飞行时的一组动力系数[18],导弹飞行速度V=885 m/s,转动惯量Jz=147 kg·m2,重力加速度g=9.81 m/s2,aωz=0.468 8 s-1,aα=99.561 5 s-2,aδe=96.518 5 s-2,bα=0.749 2 s-1,bδe=0.078 7 s-1,a′δe=29.551,b′δe=0.024 4,ωδ=120,ξ=0.7,τ=0.02.假设发动机引流直接力装置没有响应延迟,具有连续工作特性,最大推力fmax=3 600 N,仿真步长T=0.001 s.控制器参数设计如下:a=4.5,b=14.5,a1=18,b1=20,η=1,m=27,n=23,p=17,q=23.动态控制分配权重矩阵设计为
本文所设计的基于固定时间收敛的滑模控制律(14)和动态控制分配技术式(25)作用下的仿真结果如图 3~8所示.
|
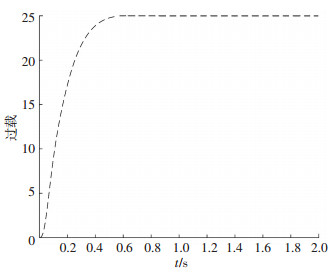
图 3 复合控制过载响应 Fig. 3 Overload response of blended control |
|
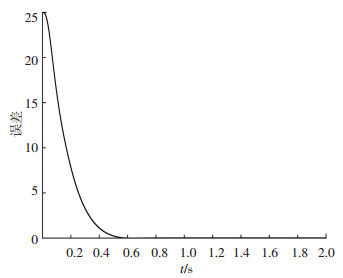
图 4 过载跟踪误差曲线 Fig. 4 Curve of the overload tracking error |

|
图 5 攻角曲线 Fig. 5 Curve of angle of attack |
|
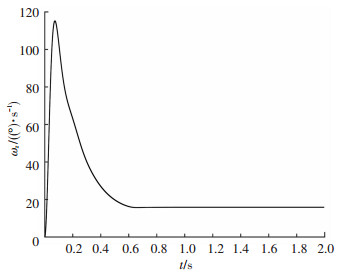
图 6 俯仰角速度曲线 Fig. 6 Curve of pitch angle rate |

|
图 7 舵偏角响应曲线 Fig. 7 Angle of aerodynamic deflector response |
|
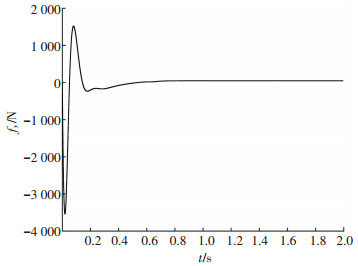
图 8 直接力响应曲线 Fig. 8 Lateral thrusters response |
图 3、4分别为系统过载跟踪响应和过载跟踪误差曲线,可以看出在过载指令发出的0.6 s左右,实际输出就跟踪上指令,系统不存在超调,复合控制的输出能够快速稳定地跟踪输入过载指令,过载跟踪误差曲线在0.6 s左右收敛到0附近.
图 5、6分别为攻角曲线和俯仰角速度曲线,可以看出25g过载对应的攻角为21°,在0.6 s左右,攻角达到其稳态值.直接力/气动力复合控制可以迅速建立起角速度,在0.11 s左右时俯仰角速度达到最大值115°/s.
图 7、8表示执行机构响应曲线.当直接力装置处于最大值时,升降舵偏转最大,即最大程度地使用了气动操纵面.舵偏角和直接力变化情况基本一致,当舵偏角为负时,直接力也基本为负,因为图 1所示弹体系中,直接力与舵偏产生的气动力变化情况刚好是相同的,说明采用基于二次规划的控制分配策略能够很好的实现各操纵机构的联合工作.
根据式(27)得到复合控制系统保守收敛时间为2 s,而过载跟踪误差收敛时间在0.6 s左右,即过载跟踪误差实现了在固定时间内收敛.
4 结论研究了空空导弹直接力/气动力复合控制系统固定时间收敛问题,针对俯仰平面的复合控制系统,对数学模型进行了分析,基于简化的数学模型,提出了一种固定时间收敛的滑模控制方法,实现过载跟踪误差在指定时间内收敛.同时在考虑执行机构动态特性的基础上,采用基于二次规划控制分配策略将虚拟控制输入分别映射到升降舵和直接力装置.理论和仿真结果表明,所设计的导弹复合控制系统,可以实现对直接力和气动力的协调使用和对过载的快速精确跟踪.
| [1] |
高建军. 空空导弹直接力控制技术[J]. 战术导弹控制技术, 2011, 28(3): 24. GAO Jianjun. The reaction jet technology of air-to-air missiles[J]. Control Technology of Tactical Missile, 2011, 28(3): 24. |
| [2] |
黄传群, 陈遵君. 防控新丁——记英国"通用防空模块导弹"(CAMM)[J]. 舰载武器, 2011, 12: 80. HUANG Chuanqun, CHEN Zunjun. Development of the UK Common Anti-Air Modular Missile[J]. Shipborne Weapons, 2011, 12: 80. |
| [3] |
KIM S, CHO D, KIM H J. Force and moment blending control for agile dual missiles[C]//2013 American Control Conference. Washington DC: IEEE, 2013: 5574. DOI: 10.1109/ACC.2013.6580710
|
| [4] |
贺成龙, 陈欣, 杨一栋. 一种动态逆解算的RLV混合规划控制分配研究[J]. 系统工程与电子技术, 2010, 32(9): 1973. HE Chenglong, CHEN Xin, YANG Yidong. Mixed programming control allocation for reusable launch vehicles using dynamic inverse calculating[J]. Systems Engineering and Electronics, 2010, 32(9): 1973. DOI:10.3969/j.issn.1001-506X.2010.09.39 |
| [5] |
马克茂, 赵辉. 一类多执行机构系统的滑模控制设计及其应用[J]. 控制理论与应用, 2011, 28(4): 556. MA Kemao, ZHAO Hui. Sliding modes control design for a class of systems with multiple actuators and its applications[J]. Control Theory & Applications, 2011, 28(4): 556. |
| [6] |
KIM S, CHO D, KIM H J. Force and moment blending control for fast response of agile dual missiles[J]. IEEE Transactions on Aerospace & Electronic Systems, 2016, 52(2): 938. DOI:10.1109/TAES.2015.140169 |
| [7] |
胥彪, 周荻. 基于反步法及控制分配的导弹直接侧向力/气动力复合控制[J]. 系统工程与电子技术, 2014, 36(3): 527. XU Biao, ZHOU Di. Backstepping and control allocation for dual/propulsive missile control[J]. Systems Engineering and Electronics, 2014, 36(3): 527. DOI:10.3969/j.issn.1001-506X.2014.03.19 |
| [8] |
李权, 周荻. 基于状态依赖Riccati方程的复合控制导弹自动驾驶仪设计[J]. 系统工程与电子技术, 2012, 34(7): 1445. LI Quan, ZHOU Di. Design of autopilot for blended controlled missiles via state-dependent Riccati equation[J]. Systems Engineering and Electronics, 2012, 34(7): 1445. DOI:10.3969/j.issn.1001-506X.2012.07.26 |
| [9] |
邹晖, 陈万春, 殷兴良. 具有侧向脉冲推力的旋转导弹建模与控制研究[J]. 系统工程与电子技术, 2005, 27(4): 687. ZOU Hui, CHEN Wanchun, YIN Xingliang. Modeling and control of a spinning missile with blended aero-fin lateral impulsive thrust[J]. Systems Engineering and Electronics, 2005, 27(4): 687. DOI:10.3321/j.issn:1001-506X.2005.04.030 |
| [10] |
闫亮, 段朝阳, 张公平, 等. 一种采用脉冲调制器的空空导弹直/气复合控制系统稳定性研究[J]. 导航定位与授时, 2017, 4(1): 42. YAN Liang, DUAN Chaoyang, ZHANG Gongping, et al. Research on the stability of an air-to-air missile lateral thrust and aerodynamic compound control system with a pulse modulator[J]. Navigation Positioning and Timing, 2017, 4(1): 42. DOI:10.19306/j.cnki.2095-8110.2017.01.008 |
| [11] |
周锐. 基于模糊逻辑的导弹复合控制系统优化设计[J]. 控制与决策, 2006, 21(7): 825. ZHOU Rui. Design of missile blended control system based on fuzzy logic[J]. Control and Decision, 2006, 21(7): 825. DOI:10.3321/j.issn:1001-0920.2006.07.024 |
| [12] |
刘皓, 沈毅. 敏捷导弹复合控制策略[J]. 系统工程与电子技术, 2011, 33(4): 874. LIU Hao, SHEN Yi. Blended control strategy for agile missiles[J]. Systems Engineering and Electronics, 2011, 33(4): 874. DOI:10.3969/j.issn.1001-506X.2011.04.32 |
| [13] |
周锐, 高晓颖. 导弹复合控制系统的多目标优化设计[J]. 航天控制, 2007, 25(2): 9. ZHOU Rui, GAO Xiaoying. Blended control system design of missile with aerodynamic fin and side thruster using multi-objective optimization[J]. Aerospace Control, 2007, 25(2): 9. DOI:10.3969/j.issn.1006-3342.2007.02.003 |
| [14] |
HUO Xin, PENG Jiping, MA Kemao, et al. A pitch autopilot design for blended aero and reaction-jet air-to-air missile via piecewise sliding mode control[C]// 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC). Nanjing: IEEE, 2016: 2181. DOI: 10.1109/CGNCC.2016.7829130
|
| [15] |
CHANG Yafei, YUAN Ruyi, FAN Guoliang, et al. A blended autopilot for dual control missile using generalized predictive and adaptive terminal sliding mode control[J]. IFAC Proceedings Volumes, 2014, 47(3): 2515. DOI:10.3182/20140824-6-ZA-1003.01229 |
| [16] |
林德福, 王辉, 王江, 等. 战术导弹自动驾驶仪设计与制导律分析[M]. 北京理工大学出版社, 2012: 9. LIN Defu, WANG Hui, WANG Jiang, et al. Autopilot design and guidance law analysis for tactical missiles[M]. Beijing Institute of Technology Press, 2012: 9. |
| [17] |
THUKRAL A, INNOCENTI M. A sliding mode missile pitch autopilot synthesis for high angle of attack maneuvering[J]. IEEE Transactions on Control Systems Technology, 1998, 6(3): 359. DOI:10.1109/87.668037 |
| [18] |
赵玉杰, 廖志忠, 段朝阳, 等. 基于终端滑模的直接力/气动力复合控制系统设计[J]. 导航定位与授时, 2015, 2(3): 49. ZHAO Yujie, LIAO Zhizhong, DUAN Chaoyang, et al. Design of blended lateral thrust and aerodynamic control system based on terminal sliding mode[J]. Navigation Positioning and Timing, 2015, 2(3): 49. DOI:10.3969/j.issn.2095-8110.2015.03.008 |
| [19] |
ZUO Zongyu, LIN Tie. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Systems Science, 2014, 47(6): 1. DOI:10.1080/00207721.2014.925608 |
| [20] |
HÄRKEGÅRD O. Dynamic control allocation using constrained quadratic programming[J]. Journal of Guidance Control & Dynamics, 2009, 27(6): 1028. DOI:10.2514/6.2002-4761 |
 2019, Vol. 51
2019, Vol. 51


