2. 中国科学技术大学 科学岛分院, 合肥 230026;
3. 光学辐射重点实验室, 北京 100854
2. Branch School of Science Island, University of Science and Technology of China, Hefei 230026, China;
3. Science and Technology on Optical Radiation Laboratory, Beijing 100854, China
随着微波遥感的发展,毫米波遥感技术得到了更多的关注和利用,这主要利益于毫米波段位于红外与普通微波之间的中间区域,除具有微波共性外,还有其优于一般微波的性能,因此,毫米波遥感在微波遥感领域发挥着越来越重要的作用[1].其中,W波段毫米波的频谱范围覆盖75~110 GHz,是毫米波的重要工作频段.在这一波段,大气对电磁波的传输信号产生吸收效应,吸收机理主要是空气分子的振动和转动跃迁,对大气传输特性的合理分析和预测对毫米波探测、通讯等系统设计具有重要的现实意义[2-3].在自然大气成分中,对毫米波的主要吸收气体有水汽、氧气、臭氧、一氧化二氮、一氧化碳、甲烷等[4-5].国内外较多的研究工作集中在水汽和氧气对毫米波的吸收特性上,吸收谱的模式大多采用近似公式或经验公式[6],对于其他分子的吸收特性研究较少.例如Rosenkranz计算了微波氧气吸收系数[7],Waters计算了水汽吸收系数[8],Liebe提出了MPM(millimeter wave propagation model)修正模型,考虑了29条水汽和44条氧气强吸收线[9],该模型得到了世界各国研究人员的认可,并成为大气毫米波实际应用的参考模型之一[10].毫米波在对流层的传输中,水汽和氧气是产生信号衰减的主要因素,但在斜程到空间的传输或不同高度上的水平传输过程中,由于各种气体分子的浓度随高度变化,对毫米波信号衰减的程度也不相同,因此研究传输路径上各吸收气体对信号的衰减作用是十分必要的.
本文基于HITRAN2008大气分子吸收光谱参数数据库,分析了水汽、氧气、臭氧、甲烷等大气主要成分的吸收谱线,充分考虑谱线远翼吸收作用,利用逐线计算方法(LBL)计算了这些气体分子在W波段的吸收谱,对W波段毫米波在均匀和非均匀传输路径上的大气衰减效应进行分析.
1 大气传输特性计算模型大气传输的吸收无论是在远红外波段、亚毫米波段还是毫米波段,其理论依据仍是以分子的能级跃迁产生吸收而使传输能量消耗.当分子从高能级到低能级状态跃时,对毫米波的吸收出现在某些离散的频率上,表征分子吸收谱线的物理参数包括谱线的中心波长、谱线强度S、谱线半宽度a,线型函数F.单个分子在一种跃迁下的吸收谱线如图 1所示,对于多种能级跃迁或多种分子的吸收情况,要对每个吸收谱线进行求和,才能得到总的吸收系数.严格地在数学上对每个谱线进行求和的计算方法为逐线计算法,计算公式为
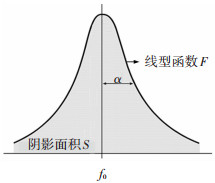
|
图 1 分子吸收谱线的特征参数 Fig. 1 Characteristic parameters of molecular absorption spectral line |
| $ k(f) = \sum\limits_i {{S_i}} F. $ |
其中:k(f)总吸收系数,f为需要计算的频率,Si为第i条谱线的积分强度,F表示线型函数.
大气透过率与吸收系数的关系式为
| $ \tau = {\rm{e}}_{\Delta r}^{{\rm{ - }}\int {k{\rm{d}}r} }. $ |
其中:r为传输距离.可以看出计算毫米波大气传输首先需要确定对毫米波具有吸收作用的大气分子,然后选取合适的线型函数并计算其谱线强度,最终由吸收系数得到传输路径上的衰减.
1.1 大气主要成分对W波段毫米波吸收特性HITRAN大气分子吸收光谱参数数据库记录了主要大气成分的吸收参数[11],本文采用了HITRAN2008,分析了大气中主要成分的吸收谱线随波段的分布情况,如表 1所示.
| 表 1 吸收谱线分布 Tab. 1 Absorption spectral line distribution |
由表 1数据可以看出,水汽、氧气在W波段均没有吸收线,而臭氧、一氧化二氮、一氧化碳和甲烷存在若干吸收谱线,因此,在后续的衰减计算过程中重点考虑水汽、氧气毫米波段的吸收谱线对W波段的远翼吸收作用,以及臭氧、一氧化二氮、一氧化碳和甲烷在W波段的吸收作用.
1.2 分子谱线吸收线型函数吸收谱线的线型函数由谱线增宽机制决定,通常分为Lorentz线型、Doppler线型以及同时考虑上述两种线型的Voigt混合线型,Lorentz线型适用于稠密气体条件,Doppler线型适用于稀薄气体条件,Voigt线型不仅适用于两者之间的中间状态,也适用于稠密大气和稀薄大气条件[12-13]. Voigt线型的一般表达式为
| $ {F_{\rm{L}}}\left( {f, {f_0}} \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\frac{{{a_{\rm{L}}}}}{{{{\left( {f - {f_0}} \right)}^2} + {a_{\rm{L}}}^2}}, $ |
| $ {F_{\rm{D}}}\left( {f, {f_0}} \right) = \frac{1}{{{a_{\rm{D}}}}}\sqrt {\frac{{\ln 2}}{{\rm{ \mathsf{ π} }}}} \exp \left[ { - 1.2\left( {\frac{{f - {f_0}}}{{{a_{\rm{D}}}}}} \right)} \right], $ |
| $ {F_{\rm{V}}}\left( {f, {f_0}} \right) = {F_{\rm{L}}}\left( {f, {f_0}} \right){F_{\rm{D}}}\left( {f, {f_0}} \right). $ |
为了补偿谱线的远翼吸收,Gross提出了动力线型[8],该线型是在实验室谱线测量数据的基础上统计得到的,具体公式为
| $ \begin{array}{l} {F_{\rm{G}}}\left( {f, {f_0}} \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\frac{{4f{f_0}{a_{\rm{L}}}}}{{{{\left( {{f^2} - {f_0}^2} \right)}^2} + 4{f^2}{a_{\rm{L}}}^2}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{a_{\rm{L}}} = {a_0}\left( {\frac{P}{{{P_0}}}} \right)\sqrt {\frac{{{T_0}}}{T}} . \end{array} $ |
其中:FV(f, f0)为Voigt线型函数;FL(f, f0)为Lorentz线型函数;FD(f, f0)为Doppler线型函数;FG(f, f0)为动力线型;f0为谱线的中心频率;aL为Lorentz谱线半宽度;aD为Doppler谱线半宽度;α0为参考态谱线半宽(温度T0=296 K, 压强P0=1.013 25×10-5 Pa);P为气体总压;T为绝对温度.
1.3 大气物理参数为了能够计算斜程或不同高度水平路径的大气衰减,需要大气物理参数随高度的分布数据,具体为温度、压力、湿度、主要组分的密度等数据,本文所有廓线数据均采用了1976美国标准大气数据,温度、压力等廓线数据见参考文献11. 表 2给出了吸收气体密度随高度的分布情况.
| 表 2 0~100 km主要吸收气体密度表 Tab. 2 Density of the main absorption gases in 0-100 km |
吸收谱线的确定考虑了谱线吸收强度以及谱线远翼吸收两个因素.为了充分计算水汽和氧气的远翼吸收,水汽选取20~1100 GHz的92条吸收线,氧气选取50~850 GHz的106条吸收线,谱线分布见图 2(b).臭氧、一氧化二氮、一氧化碳、甲烷的谱线选取波段为30~300 GHz.谱线分布见图 2(c)~2(d).
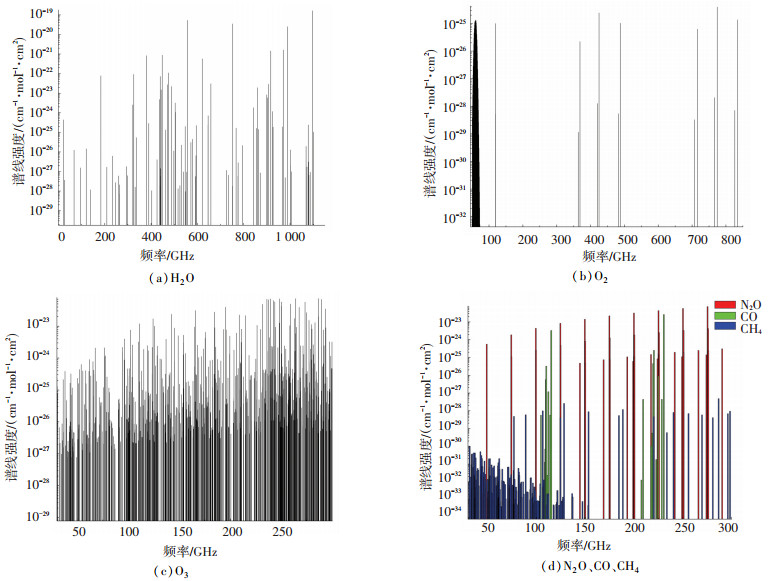
|
图 2 吸收谱线分布图 Fig. 2 Distributiondiagram of absorption spectral line |
从谱线强度来看,水汽的吸收谱线强度最大,均值为10-24cm-1/(mol·cm-2),高于其他分子的吸收谱线强度,最大值为10-19cm-1/(mol·cm-2).甲烷的吸收谱线强度均值最小,为10-33cm-1/(mol·cm-2).从谱线随频率的分布来看,氧气的吸收谱线集中在50~70 GHz,出现谱线重叠.一氧化二氮、一氧化碳的吸收谱线集中在100~230 GHz.水汽、臭氧、甲烷的谱线分布随频率分布较均匀.
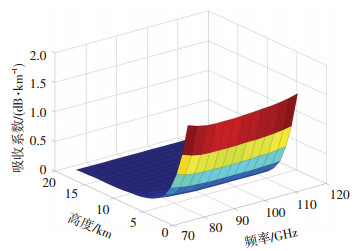
将大气数据中的温度、压力廓线数据代入式(6)、(7),即可求得每根谱线的线型函数,再由式(1)可计算出不同大气高度的吸收系数谱,如图 3所示.

|
图 3 吸收曲线 Fig. 3 Absorption curves |
从图 3中数据可以看出,气体的吸收系数与其在大气中的密度分布密切相关,密度大吸收系数也大,密度小吸收系数也相应减小.水汽、氧气、一氧化二氮、一氧化氮、甲烷吸收系数最大值均为近地面0 km高度,臭氧的吸收系数最大值出现在20 km左右高度.从各图的数据对比来看,水汽的吸收系数最大,且与频率成线性,在110 GHz达到1.6 dB/km.氧气的吸收系数最大值为0.22 dB/km,吸收系数曲线在100 GHz出现一个凹谷.臭氧的吸收系数分别在93.9、96.3 GHz出现两个尖峰,吸收系数最大值为5.5×10-3 dB/km.一氧化二氮在75.3、100.5 GHz出现两个尖峰,吸收系数最大值为6×10-5 dB/km.一氧化碳的吸收系数随频率的增加而增大,最大值为5×10-6 dB/km.甲烷的吸收系数分别在77.4、88.2、105.6 GHz出现3个尖峰,吸收系数最大值为10-8 dB/km.将各气体的吸收系数进行求和,即可得到总的吸收系数[14-15]. 图 4为0~20 km不同大气高度吸收系数变化图.从图中数据可以看出,吸收系数随频率增加而增大,基本呈线性趋势,此外,吸收系数还随大气高度增加而减小,当高度升至10 km,吸收系数下降为10-2 dB/km,即毫米波信号在近地面稠密大气的衰减强烈.
|
图 4 总的吸收系数分布图 Fig. 4 Distribution diagram of total absorption coefficient |
得到吸收系数后,利用式(2)即可计算不同传输路径的大气衰减.均匀大气传输路径为该段距离的大气温度、压强等参数不变,一般用于水平探测衰减的计算. 图 5为温度为288 K,压强为1.013×105 Pa,传输距离分别为1、5、10 km的透过率变化曲线.可以看出,透过率随传输距离增加而减小.
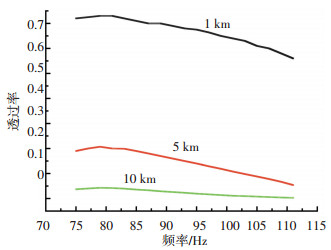
|
图 5 透过率变化曲线图 Fig. 5 Transmission curves |
非均匀大气传输路径是指温度、压强、空气密度等表征大气状态的参数发生变化,具体计算所需参数参照1976美国标准大气数据. 图 6为压强不变,温度改变时透过率的变化情况,计算条件为压强1.013×105 Pa,传输路径为1 km,温度分别为T1(273 K)、T2(288 K)、T3(300 K).可以看出,当压强和传输距离一定,温度越高,透过率越大.
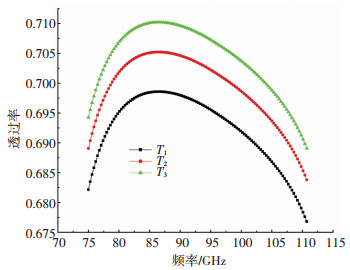
|
图 6 透过率变化曲线图 Fig. 6 Transmission curves |
图 7为温度不变,压强改变时透过率的变化情况,计算条件为温度288 K,压强分别为P1(1.013×105 Pa)、P2(8.9×104 Pa)、P3(7.9×104 Pa).可以看出,当温度和传输距离一定,压强越高,透过率越小.
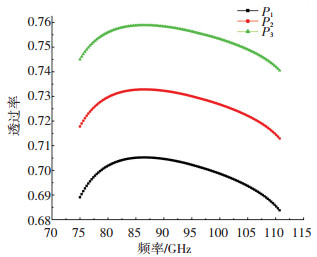
|
图 7 透过率变化曲线图 Fig. 7 Transmission curves |
综合图 5、6的计算结果,可进一步推断出靠近地面的大气比高空大气对毫米波信号的衰减强烈,因为通常低空大气温度高且压强大.
整层大气的衰减计算方法是将大气按照高度分层,认为每一层大气性质相同,分别计算各个高度大气层的单层大气透过率后,将各层透过率求和,可得到整个大气层传输路程上总透过率谱.计算条件为大气高度为0~100 km,各层厚度为1 km,大气模式为1976美国标准大气模式,计算结果如图 8所示.从图中结果可以看出,各层的透过率随高度的增加而增大,10 km之后的透过率达到0.99.
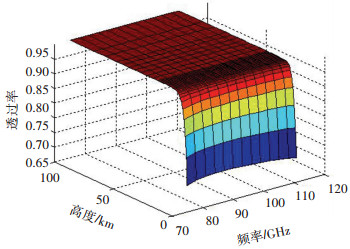
|
图 8 非均匀路径透过率变化曲线图 Fig. 8 Transmission curves in inhomogeneous path |
将本文计算结果与Liebe模型计算结果进行比对,结果如图 9所示.计算条件为1976美国标准大气模式,垂直向下观测100 km传输路径.
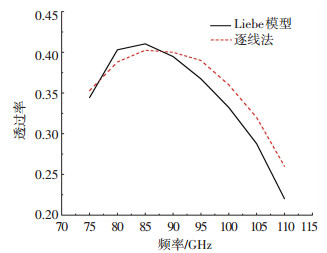
|
图 9 透过率计算结果对比图 Fig. 9 Comparison of the calculated results of transmission |
图中虚线为逐线法计算结果,实线为Liebe模型计算结果,从对比结果来看,两条曲线变化趋势一致,在80~90 GHz吸收线集中的峰值附近偏差较小,在偏离吸收峰的90~110 GHz波段偏差较大,最大偏差为15%,原因为Liebe模型考虑了两种主要吸收气体水汽(29条谱线)和氧气的谱线吸收(44条谱线),逐线法考虑了92条水汽和106条氧气吸收线,且加入了臭氧、一氧化碳、甲烷等微量吸收气体的吸收作用,以此提高计算精度.此外,Liebe模型将吸收分成谱线吸收和连续吸收两部分进行衰减计算,逐线法采用Gross动力线型对谱线远翼的吸收进行修正.产生连续吸收的物理机制尚未确定,目前较认可的说法是强吸收线的远翼产生的,也就是说修正吸收线的远翼线型是提高吸收系数计算精度的主要工作之一.此外,利用94 GHz的测试系统进行水平传输测量,发射端和接收端距离为100 m,发射功率为60 mW,测量时间为2017年8月9日,环境参数:温度为293 K,压强为1.013×105 Pa,相对湿度为60%,测量的能量衰减为0.161 8 dB,本文的模型计算结果为0.155 8 dB,相对偏差为3.7%,验证了理论模型的正确性.
4 结论1) 大气中各吸收气体对毫米波的衰减作用与其密度相关,密度越大衰减作用越强.水汽、氧气对毫米波的衰减严重,且集中0~10 km大气高度,其他成分对毫米波的衰减较弱.
2) 通过逐线法与Liebe模型方法计算结果分析,建立精确的远翼吸收线型函数是提高衰减计算精度的重要工作.
3) 利用94 GHz的测试系统进行了水平传输路径的测量数据与理论计算数据比对,验证了理论计算模型的精度。由于受到测试设备和测试场地的限制,今后将继续深入开展斜程及水平远距离传输测试研究。
| [1] |
FUKAO S, HAMAZU K, DOVIAK R J. Radar for meteorological and atmospheric observations[M]. Heidelberg: Springer, 2014: 5.
|
| [2] |
张颖, 李悠. 面向太赫兹应用的平面结构聚合物电光传感器[J]. 仪器仪表学报, 2017, 38(5): 1227. ZHANG Ying, LI You. Electro-optic polymer sensor with coplanar electrodes structure for THz applicaition[J]. Chinese Journal of Scientific Instrument, 2017, 38(5): 1227. |
| [3] |
周亮, 王振环, 孙东辰, 等. 现代精密测量技术现状及发展[J]. 仪器仪表学报, 2017, 38(8): 1870. ZHOU Liang, WANG Zhenhuan, SUN Dongchen, et al. Present situation and development of modern precision measurement technology[J]. Chinese Journal of Scientific Instrument, 2017, 38(8): 1870. |
| [4] |
石广玉. 大气辐射学[M]. 北京: 科学出版社, 2008: 84. SHI Guangyu. Atmospheric radiation[M]. Beijing: Science Press, 2008: 84. |
| [5] |
王金虎, 葛俊祥, 魏鸣, 等. 两种相态降水粒子对微波、毫米波衰减特性的影响分析[J]. 遥感技术与应用, 2017, 32(6): 1048. WANG Jinhu, GE Junxiang, WEI Ming, et al. Effects analysis of two-phase precipitations on microwave and millimeter-wave attenuation characteristics[J]. Remote Sensing Technology and Application, 2017, 32(6): 1048. |
| [6] |
聂伟, 阚瑞峰, 许振宇, 等. 基于TDLAS技术的水汽低温吸收光谱参数测量[J]. 物理学报, 2017, 66(20): 204204. NIE Wei, KAN Ruifeng, XU Zhenyu, et al. Measuring spectral parameters of water vapor at low temperature based on tunable diode laser absorption spectroscopy[J]. Acta Physica Sinica, 2017, 66(20): 204204. DOI:10.7498/aps.66.204204 |
| [7] |
ROSENKRANZP W. Shape of the 5 mm oxygen band in the atmosphere[J]. IEEE Trans on Antennas and Remote Sensing, 1975(4): 198. |
| [8] |
刘亚旭.大气毫米波辐射特性及应用研究[D].南京: 南京理工大学, 2010: 14 LIU Yaxu. Atmospheric millimeter wave radiation characteristics and application[D]. Nanjing: Nanjing University of Science and Technology, 2010 |
| [9] |
LIEBE H J. MPM—an atmospheric millimeter-wave propagation model[J]. International Journal Infrared and Millimeter Waves, 1989, 10(6): 631. DOI:10.1007/BF01009565 |
| [10] |
唐义平, 李卫, 李兴国, 等. 亚毫米波的大气传输研究[J]. 红外与激光工程, 1997, 26: 26. TANG Yiping, LI Wei, LI Xingguo. Research on the atmospheric transmission characteristics of submillimeter wave[J]. Infrared and Laser Engineering, 1997, 26: 26. |
| [11] |
饶瑞中. 现代大气光学[M]. 北京: 科学出版社, 2015: 115. RAO Ruizhong. Modern atmospheric optics[M]. Beijing: Science Press, 2015: 115. |
| [12] |
谈和平, 夏新林, 刘林华, 等. 红外辐射特性与传输的数值计算:计算辐射学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006: 73. TAN Heping, XIA Xinlin, LIU Linhua, et al. Numerical computation of infrared radiation characteristics and transmission: computational radiation[M]. Harbin: Harbin Institute of Technology Press, 2006: 73. |
| [13] |
董世奎, 谈和平, 余其铮, 等. 300~3000 K水蒸气红外辐射谱带模型参数[J]. 热能动力工程, 2001, 16(1): 33. DONG Shikui, TAN Heping, YU Qizheng, et al. Infrared radiative spectral band-model parameters for water vapor in the 300-3000 K temperature range[J]. Journal of Engineering for Thermal Energy and Power, 2001, 16(1): 33. DOI:10.3969/j.issn.1001-2060.2001.01.009 |
| [14] |
宋立众, 聂玉明, 段舒雅. 一种电磁耦合馈电双极化毫米波微带天线设计[J]. 哈尔滨工业大学学报, 2015, 47(11): 93. SONG Lizhong, NIE Yuming, DUAN Shuya. Design of a dual polarized millimeter wave microstrip antenna fed by electromagnetic coupling[J]. Journal of Harbin Institute of Technology, 2015, 47(11): 93. |
| [15] |
张超, 朱莉, 林琳. 毫米波/亚毫米波大气传输特性研究[J]. 微波学报, 2015, 31(增刊2): 14. ZHANG Chao, ZHU Li, LIN Lin. Research on the atmospheric transmission characteristics of millimeter wave/submillimeter wave[J]. Journal of Microwaves, 2015, 31(S2): 14. |
 2019, Vol. 51
2019, Vol. 51


