2. 哈尔滨工业大学 电气工程及自动化学院, 哈尔滨 150001
2. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
DOA估计是一种利用阵列接收信号获取信号方向信息的技术,被广泛应用于雷达、声呐、无线通信和地震学的研究[1-2].在过去几十年中,均匀线阵由于其构造简单,成为应用最多的阵列几何模型,但是当被测信号源数目接近阵元数目时,估计精确度降低,可估计的信号源数目受阵元数目的限制.而且在均匀线阵下,为避免角度模糊,阵元间距离被限制在信号半波长内,这使得阵列孔径受到限制,继而限制了分辨率的提高.在实际应用中,例如5G超密度蜂窝网络下[3],为保证DOA估计算法的自由度和分辨率,大量的阵元数目和相关射频模块会使计算复杂度和硬件成本急剧增加.近年来,逐渐兴起的互质阵列几何模型可以很好地解决上述问题[4].互质阵突破了阵元间距对阵列孔径的限制,提高了DOA估计算法的分辨率,且在相同阵元数目的情况下具有更高的自由度,很好地平衡了估计性能和复杂度问题.与传统的稀疏阵列相比,如最小冗余阵[5]和最小孔阵列[6],互质阵的系统简洁、结构灵活,因而引起了信号处理领域学者的极大关注,具有广阔的应用前景.
多重信号分类技术[7]是解决DOA估计最重要的方法之一,通过对频谱进行谱峰搜索来获得角度估计值.但是为了保证较高的估计分辨率而设定一个小的空间谱搜索间距时,会造成计算量急剧增多.旋转不变子空间技术是另一种重要的适用于均匀线阵的子空间类DOA估计算法.文献[8-9]中介绍了基于稀疏阵列的ESPRIT-like算法,由一对稀疏互质的均匀线阵分别获得接收信号,再根据互质关系[10],通过解相位模糊获得唯一的DOA估计解,但这种算法没有充分利用稀疏阵列对有效孔径的扩展,DOA估计的自由度也没有实质性的提高.为充分利用互质阵的自由度优越性,本文将ESPRIT算法引入阵列优化领域,从互质优化阵中选择一对具有相同均匀线阵几何结构的子阵列,由子阵列的位移不变性可推出信号子空间之间的旋转不变性.基于推导出的互质阵协方差矩阵,研究了子阵列信号子空间的旋转算子,并通过对旋转算子特征值分解得到DOA估计值.为进一步降低计算量,本文通过酉变换将协方差矩阵从复数域转换到实数域,使DOA估计算法更加高效.
空间平滑方法是单快拍或信号源完全相干情况下的一种预处理技术,用来恢复协方差矩阵的秩,此外将阵列数据进行托普利兹矩阵重构[11],可以直接得到与空间平滑方法相同的信号子空间,计算量更小,实质也相当于空间平滑方法.阵列信号在进行空间平滑预处理之后,有效阵列孔径取决于平滑子阵的阵元数,因此在平滑处理后,阵列有效孔径减小,分辨率降低.文献[12]中提出了均匀线阵下的有效孔径提高方法(SSIA),但只适用于单快拍情况.文献[13]提出的算法可以在多快拍下提高有效孔径,但是只能估计个数小于阵元数的信号源.文献[14]综合了二者的优点,可以在多快拍下提高有效孔径且精确度有所提高,但由于是均匀线阵,估计自由度受限.为了进一步增大有效阵列孔径,提高估计分辨率和自由度,本文提出一种基于互质阵列的矩阵重叠预处理技术,将空间平滑后的阵列协方差矩阵重叠,利用重叠后的矩阵进行角度估计.矩阵重叠扩展了阵列孔径,又因为空间平滑协方差矩阵分割出的两个子阵具有相同的信号子空间,算法具有可行性.文章提出的算法优于现有算法,进行了充分的仿真实验验证,相比重叠之前,分辨率和精确度均有提高.
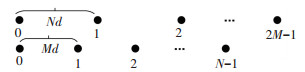
1 互质阵列和信号模型建立 1.1 互质阵列互质阵列由两个间距不等的均匀线阵交替组成,这两个均匀线阵的阵元间距等于半波长的整数倍,且这两个倍数是一对互质的整数. 图 1是互质阵列几何模型的一种,构成互质阵的两均匀线阵如图 2所示,阵元数目分别为2M、N(M < N),对应的阵元间距分别为Nd、Md.其中M, N为互质的整数,d=λ/2,λ为入射波波长.两均匀线阵的阵元位置分别表示为

|
图 1 互质阵阵元位置 Fig. 1 The non-uniform coprime array |
|
图 2 构成互质阵的两个均匀线阵 Fig. 2 The two uniform linear arrays consructing the coprime array |
| $ {S_1} = \left\{ {0,Nd,2Nd, \cdots ,\left( {2M - 1} \right)Nd} \right\}, $ | (1) |
| $ {S_2} = \left\{ {0,Md,2Md, \cdots ,\left( {N - 1} \right)Md} \right\}, $ | (2) |
式中S1、S2为两个间距不等的均匀线阵,互质阵列的阵元位置为S=S1∪S2.
1.2 信号模型设空间有K个远场窄带不相关信号源,这些信号以不同的方位角θ1, θ2, ..., θK,θk∈[-π/2, π/2)入射到互质阵列上,t时刻阵列的输出信号数学模型为
| $ {x_s}(t) = \sum\limits_{k = 1}^K a \left( {{\theta _k}} \right){s_k}\left( t \right) + n\left( t \right) = \mathit{\boldsymbol{A}}s\left( t \right) + n\left( t \right), $ | (3) |
| $ \mathit{\boldsymbol{A}} = \left[ {a\left( {{\theta _1}} \right),a\left( {{\theta _2}} \right), \cdots ,a\left( {{\theta _K}} \right)} \right] \in {C^{(2M + N - 1) \times K}}, $ | (4) |
| $ \mathit{\boldsymbol{a}}\left( {{\theta _k}} \right) = {\left[ {1, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{d_i}\sin {\theta _k}}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{d_{2M + N - 1}}\sin {\theta _k}}}} \right]^{\rm{T}}}. $ | (5) |
式中:A为阵列导向矢量矩阵,s(t)为零均值信号矢量,n(t)为零均值高斯白噪声,di∈S表示第i个阵元相对参考阵元点的位置,βk=(2πd/λ)sinθk表示空间频率,θk为DOA估计值.根据以上定义可得阵列的协方差矩阵为
| $ {\mathit{\boldsymbol{R}}_{{\rm{xs}}}}\left( t \right) = E\left[ {\mathit{\boldsymbol{x}}\left( t \right){\mathit{\boldsymbol{x}}^{\rm{H}}}\left( t \right)} \right] = \sum\limits_{k = 1}^K {\sigma _k^2} \mathit{\boldsymbol{a}}\left( {{\theta _k}} \right){\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {{\theta _k}} \right) + \sigma _n^2\mathit{\boldsymbol{I}}, $ | (6) |
式中:σk2为第k个信号功率,σn2为噪声方差,I为单位阵.
2 空间平滑矩阵重叠算法 2.1 算法详述协方差矩阵的表达式a(θk)aH(θk)中有
| $ {S_{{\rm{diff}}}} = \left\{ {{d_p} - {d_q}|{d_p},{d_q} \in S} \right\}, $ | (7) |
式中Sdiff按升序排列,这样可利用的阵元数目从|S|就上升到了Sdiff.由于互质阵列的特殊构造使得Sdiff在原点附近包含一个均匀线阵,记为SdiffULA.对于阵元数目分别为2M、N的均匀线阵构成的互质阵列,虚拟阵元均匀部分阵元数目为2MN+2M-1,图 3为M=3, N=5时,互质阵列的实际阵元位置、虚拟阵元位置以及虚拟阵元均匀部分位置.
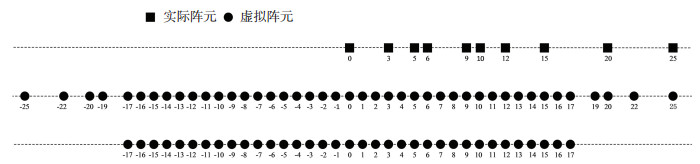
|
图 3 互质阵列实际阵元位置、虚拟阵元位置、虚拟阵元均匀部分位置 Fig. 3 The actual array, virtual array, and uniform part of virtual array of the coprime array |
为获得虚拟阵列的接收信号信息,首先将协方差矩阵Rxs(t)转换为列向量
| $ {\rm{vec}}\left( {{\mathit{\boldsymbol{R}}_{\mathit{xs}}}} \right) = {\rm{vec}}\left( {\sum\limits_{k = 1}^K {\sigma _k^2} a\left( {{\theta _k}} \right){a^{\rm{H}}}\left( {{\theta _k}} \right)} \right) + \sigma _n^2{\rm{vec}}\left( \mathit{\boldsymbol{I}} \right), $ | (8) |
式中vec(·)表示矢量化(将矩阵转换为列向量).由于不同实际阵元的相位差也可能相同,因此虚拟阵列的一个阵元可能是不同的实际阵元的相位差,需要对一个相位差对应的多个相关值进行去冗余.
式(8)经过去冗余后表示为
| $ {r_{{\rm{diff}}}} = \mathit{\boldsymbol{F}}{\rm{vec}}\left( {{\mathit{\boldsymbol{R}}_{{\rm{xs}}}}} \right), $ | (9) |
式中rdiff为去冗余后的一列协方差;
| $ {\left\langle \mathit{\boldsymbol{F}} \right\rangle _{{m_0},{\rm{:}}}} = {\rm{vec}}{\left( {\mathit{\boldsymbol{Z}}\left( {{m_0}} \right)} \right)^{\rm{T}}},{m_0} \in {S_{{\rm{diff}}}}, $ | (10) |
其中矩阵Z(m0)满足
| $ \begin{array}{l} {\left\langle {\mathit{\boldsymbol{Z}}\left( {{m_0}} \right)} \right\rangle _{{d_p},{d_q}}} = \\ \left\{ {\begin{array}{*{20}{l}} {\left| {\frac{1}{{M\left( {{m_0}} \right)}}} \right|,}&{{d_p} - {d_q} = {m_0},{d_p},{d_q} \in S,}\\ 0&{其他.} \end{array}} \right. \end{array} $ | (11) |
式中M(m)为阵列权值[15],满足
| $ M\left( {{m_0}} \right) = \left\{ {\left( {{d_p},{d_q}} \right) \in {S^2}|{d_p} - {d_q} = {m_0}} \right\}. $ | (12) |
当m0∈SdiffULA时,得到
| $ {\mathit{\boldsymbol{R}}_{{\rm{ss}}}} = \left[ {\begin{array}{*{20}{c}} {{J_0}r_{{\rm{diff}}}^{{\rm{ULA}}}}&{{J_1}r_{{\rm{diff}}}^{{\rm{ULA}}}}& \ldots &{{J_{L - 1}}r_{{\rm{diff}}}^{{\rm{ULA}}}} \end{array}} \right] \in {C^{{M_{{\rm{sub}}}} \times L}}, $ | (13) |
| $ {\mathit{\boldsymbol{J}}_l} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{O}}_{{M_{{\rm{sub}}}} \times \left( {L - 1 - l} \right)}}}&{{\mathit{\boldsymbol{I}}_{{M_{{\rm{sub}}}} \times {M_{{\rm{sub}}}}}}}&{{\mathit{\boldsymbol{O}}_{{M_{{\rm{sub}}}} \times l}}} \end{array}} \right],0 \le l \le L - 1. $ | (14) |
式中Rss为空间平滑协方差矩阵,Jl为选择矩阵.实际有限快拍下,接收信号为x,有限快拍下空间平滑协方差矩阵表示为
| $ {{\mathit{\boldsymbol{\tilde R}}}_{{\rm{ss}}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_0}\tilde r_{{\rm{diff}}}^{{\rm{ULA}}}}&{{\mathit{\boldsymbol{J}}_1}\tilde r_{{\rm{diff}}}^{{\rm{ULA}}}}& \cdots &{{\mathit{\boldsymbol{J}}_{L - 1}}\tilde r_{{\rm{diff}}}^{{\rm{ULA}}}} \end{array}} \right] \in {C^{{M_{{\rm{sub}}}} \times L}}. $ | (15) |
平滑后子阵长度为Msub,只能估计数目小于Msub个的信源,阵列的有效孔径,也就是虚拟阵列有效阵元数从|SdiffULA|降到Msub,自由度和有效孔径都因平滑而减小.
针对上述问题本文提出重叠矩阵的方法,具体步骤为选定一个重叠度Δ,按列分割空间平滑协方差矩阵,分割出的子矩阵有相同的信号子空间,将分割出的两个子矩阵重叠.重叠扩张了协方差矩阵的行数,相当于增大了有效孔径.具体实现过程为
| $ {\boldsymbol{J}_{{\rm{ss1}}}} = {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}_{L - \mathit{\Delta }}}}\\ {{\boldsymbol{O}_{\mathit{\Delta } \times \left( {L - \mathit{\Delta }} \right)}}} \end{array}} \right]_{L \times \left( {L - \mathit{\Delta }} \right)}}, $ | (16) |
| $ {\boldsymbol{J}_{{\rm{ss2}}}} = {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{O}_{\mathit{\Delta } \times \left( {L - \mathit{\Delta }} \right)}}}\\ {{\boldsymbol{I}_{L - \mathit{\Delta }}}} \end{array}} \right]_{L \times \left( {L - \mathit{\Delta }} \right)}}, $ | (17) |
| $ {\boldsymbol{\tilde R}_{{\rm{aug}}}} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\tilde R}}_{{\rm{ss}}}}{\boldsymbol{J}_{{\rm{ss1}}}}}\\ {{{\boldsymbol{\tilde R}}_{{\rm{ss}}}}{\boldsymbol{J}_{{\rm{ssa}}}}} \end{array}} \right]_{2{M_{{\rm{sub}}}} \times (L - \mathit{\Delta })}}. $ | (18) |
式中J为选择矩阵,
协方差矩阵
由于
| $ T:{{\boldsymbol{\tilde R}}_{{\rm{aug}}}} \to {\boldsymbol{\tilde R}}_{{\rm{aug}}}^{\rm{T}}{\boldsymbol{\tilde R}}_{{\rm{aug}}}^{\rm{T}} = {\boldsymbol{Q}}_{2{M_{{\rm{ab}}}}}^{\rm{H}}{{\boldsymbol{\tilde R}}_{{\rm{aug}}}}{{\boldsymbol{Q}}_{(L - \mathit{\Delta })}}, $ | (19) |
其中酉矩阵Q在奇数和偶数情况表示为
| $ {\mathit{\boldsymbol{Q}}_{2n + 1}} = 1/\sqrt 2 \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&0&{{\rm{j}}{\mathit{\boldsymbol{I}}_n}}\\ 0&{\sqrt 2 }&0\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_n}}&0&{ - {\rm{j}}{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_n}} \end{array}} \right]; $ | (20) |
| $ {\mathit{\boldsymbol{Q}}_{2n}} = 1/\sqrt 2 \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&{{\rm{j}}{\mathit{\boldsymbol{I}}_n}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_n}}&{ - {\rm{j}}{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_n}} \end{array}} \right]; $ | (21) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{H}}_1} = 2Re\left\{ {\mathit{\boldsymbol{Q}}_{2m}^{\rm{H}}{\mathit{\boldsymbol{J}}_{{\rm{aug}}}}{\mathit{\boldsymbol{Q}}_{2{M_{{\rm{sub}}}}}}} \right\}.}\\ {{\mathit{\boldsymbol{H}}_2} = 2Im\left\{ {\mathit{\boldsymbol{Q}}_{2m}^{\rm{H}}{\mathit{\boldsymbol{J}}_{{\rm{aug}}}}{\mathit{\boldsymbol{Q}}_{2{M_{{\rm{sub}}}}}}} \right\};} \end{array}} \right. $ | (22) |
| $ {\mathit{\boldsymbol{J}}_{{\rm{aug}}}} = {\mathit{\boldsymbol{I}}_2} \otimes {\mathit{\boldsymbol{J}}_2}; $ | (23) |
| $ {\mathit{\boldsymbol{J}}_2} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{O}}_{m \times 1}}}&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right]. $ | (24) |
式(20)、(21)中In,Πn分别为n维单位矩阵和反对角单位阵.对酉变换后的协方差矩阵
重叠后矩阵的行数增大1倍,相当于有效孔径增大了1倍.但是自由度并没有增加1倍.自由度受两个因素影响,首先估计K个信号角度需满足(2Msub-2)≥K, 还需满足L-Δ≥K,可得(Msub)min=(K+2)/2和Lmin=K+Δ,再根据空间平滑的数量关系可知|SdiffULA|min=(Msub)min+Lmin-1=3K/2+Δ,估计K个信号至少需要3K/2+Δ个阵元,意味着单快拍下,|SdiffULA|个阵元,可估计2(|SdiffULA|-Δ)/3个信号源.当重叠度Δ取一个较小值时,趋近于2/3|SdiffULA|.而对于一对互质实数M、N实际阵元数目为2M+N-1, 可构造出|SdiffULA|=2MN+2M-1个均匀的虚拟阵元, 因此算法可估计多于实际阵元数目的信号.
以上给出了本文自由度的具体分析,下面给出理论上一般线阵的自由度情况分析.
对于任意一个线阵,定义一个集合:
| $ {A_\theta } = \left\{ {a\left( \theta \right):\theta \in \left[ { - {\rm{ \mathit{ π} }}/2,{\rm{ \mathit{ π} }}/2} \right)} \right\}, $ | (25) |
式中a(θ)为阵列导向矢量.使Aθ线性相关的最小整数记为D(Aθ)∈N.对于任意一个M元线阵,有D(Aθ)≤M+1.对于M元均匀线阵,M个导向矢量都线性独立,因此D(Aθ)=M+1.
文献[16]中给出,无噪声条件下,K个信源能被唯一估计的条件为
| $ K < \frac{{D\left( {{A_\theta }} \right) - 1 + {\rm rank}(S)}}{2}, $ | (26) |
| $ S = \left[ {s\left( 1 \right), \cdots ,s\left( L \right)} \right], $ | (27) |
式中L为采样快拍数.均匀线阵下,由于rank(S)≤K且D(Aθ)=M+1,式(26)可简化为
| $ K < D\left( {{A_\theta }} \right) - 1 \le M. $ | (28) |
文献[16]还给出,如果信号源角度固定,且信号矢量是从一些绝对连续的分布中随机抽取的,那么K个信源可以被唯一稳定估计的条件为
| $ K < \frac{{2{\rm rank}\left( S \right)}}{{2{\rm rank}\left( S \right) + 1}}\left( {D\left( {{A_\theta }} \right) - 1} \right). $ | (29) |
单快拍情况下rank(S)=1,因此式(29)中给出的DOA估计自由度接近2/3D(Aθ).然而文献[17]指出式(29)中给出的自由度值在实际有限信噪比条件下难以达到.
3 仿真及性能分析为了验证文章提出算法的有效性,将本文空间平滑(SS)矩阵重叠U-ESPRIT算法与SS U-ESPRIT算法以及SS MUSIC算法估计性能进行比较.文章采用均方根误差评价算法的精确度,均方根误差公式为
| $ E = \sqrt {\frac{1}{{QK}}\sum\limits_{q = 1}^Q {\sum\limits_{k = 1}^K {{{\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \theta } }_{k,q}} - {\theta _k}} \right)}^2}} } } , $ | (30) |
式中
首先,为了确定矩阵的最优重叠度Δ,对不同重叠度下的估计均方根误差进行比较.从图 4中可以看出,Δ在4以内波动对估计精确度影响不大,最终取Δ=2.

|
图 4 均方根误差随重叠度变化曲线 Fig. 4 E of DOA estimates vs. degree of overlapping |
图 5、6分别给出了经矩阵重叠预处理后,U-ESPRIT算法和MUSIC算法的估计拟合曲线.在快拍数为80,信噪比为0 dB条件下,估计12个均匀分布在-60°~60°之间的信号源.可以看出在互质阵列下,这两种算法都能估计数目多于阵元数的信号源,但MUSIC算法的谱峰不够尖锐,这是因为小采样快拍数或噪声干扰严重时,噪声子空间与信号子空间难以完全分离,导致噪声子空间与导向矢量的正交性变差,空间谱谱峰不尖锐,甚至出现漏峰、错峰现象,而且由于角度搜索是离散搜索,而信号源的角度分布是连续的,造成估计精确度受空间谱的搜索间距限制,但小的搜索间距又会造成计算量的急剧增加,导致MUSIC算法在计算量方面的缺陷.在Windows10系统下Intel Core i3-3217U处理器1.8 GHz主频4 GB内存环境下,对以上实验重复进行1 000次,U-ESPRIT算法和MUSIC算法所用的运算时间分别为6.07、131.48 s,后者远远大于前者,因而U-ESPRIT算法要优于MUSIC算法.
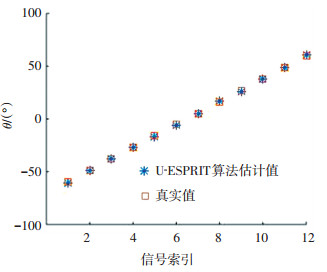
|
图 5 U-ESPRIT算法拟合曲线 Fig. 5 Fitting curve of U-ESPRIT algorithm |
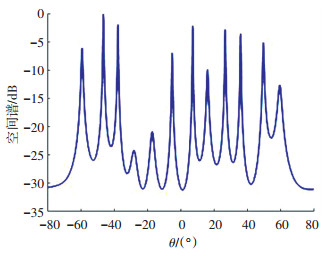
|
图 6 MUSIC算法拟合曲线 Fig. 6 Fitting curve of MUSIC algorithm |
图 7给出了采样快拍数为80,信噪比在-10 dB到25 dB变化时,均方根误差变化曲线.仿真结果为对每个信噪比采样点进行2 000次蒙特卡洛实验的统计结果.经矩阵重叠后,DOA估计精度有所提高.但在信噪比小于-5 dB时,精确度提高不明显,这是因为矩阵重叠后,噪声也被重叠.
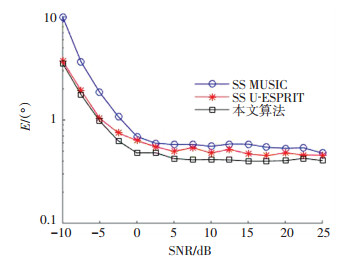
|
图 7 均方根误差随信噪比变化曲线 Fig. 7 E of DOA estimates vs. SNR |
图 8给出了信噪比为10 dB,快拍数不同时的均方根误差变化曲线.可以看出在小快拍情况下,矩阵重叠后,算法的精确度有所提高.这是由于矩阵重叠增加了协方差矩阵的数据量,在小采样快拍情况下,精确度提高更加明显.
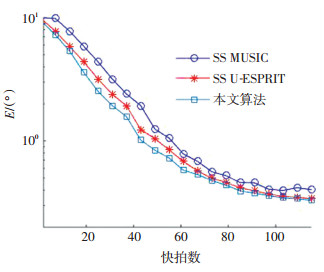
|
图 8 均方根误差随快拍数变化曲线 Fig. 8 RMSE of DOA estimates vs. snapshot |
图 9给出了互质阵列和均匀线阵两种阵列模型下,不同DOA估计算法的分辨率.可以看出与均匀线列相比,互质阵列在分辨率方面有很大优势,且经过矩阵重叠预处理后分辨率进一步提升.这是由于矩阵重叠增加了阵列的有效孔径,进而提升了分辨率.
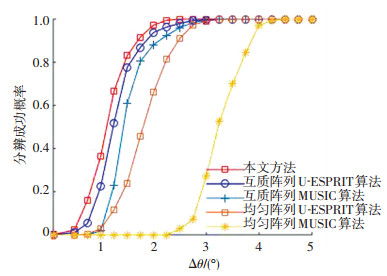
|
图 9 几种算法的分辨率比较 Fig. 9 Resolution comparison of several algorithms |
对空间平滑造成孔径损失的问题,文章提出一种互质阵列下的矩阵重叠预处理方法,该方法通过分割空间平滑协方差矩阵,将其子阵重叠来扩展阵列有效孔径,弥补了空间平滑孔径损失的问题,提高了DOA估计的分辨率和自由度.由于该方法增加了协方差矩阵的数据量,在低快拍下,估计精确度也有明显提高.文章研究表明互质阵列下U-ESPRIT算法在精确度和计算效率方面均有优势.理论分析和仿真结果均验证了该预处理方法和U-ESPRIT算法的有效性.
| [1] |
GU Yujie, ZHANG Yinin, GOODMAN N A. Optimized compressive sensing-based direction-of-arrival estimation in massive MIMO[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. New Orlean: IEEE Press, 2017: 3181
|
| [2] |
SHI Zhiguo, ZHOU Chengwei, GU Yujie, et al. Source estimation using coprime array: a sparse reconstruction perspective[J]. IEEE Sensors Journal, 2017, 17(3): 755. |
| [3] |
GE Xiaohu, TU Song, MAO Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72. |
| [4] |
VAIDYANATHAN P P, PAL P. Sparse sensing with coprime arrays[C]//Signals, Systems and Computers. Pacific Grove: IEEE Press, 2010: 1405
|
| [5] |
ZOLTOWSKI M D, SILVERSTEIN S D, MATHEWS C P. Beamspace root-MUSIC for minimum redundancy linear arrays[J]. IEEE Transactions on Signal Processing, 1993, 41(7): 2502. |
| [6] |
BLOOM G S, GOLOMB S W. Applications of numbered undirected graphs[J]. Proceedings of the IEEE, 1977, 65(4): 562. DOI:10.1109/PROC.1977.10517 |
| [7] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276. |
| [8] |
SUN Fenggang, GAO Bin, CHEN Lizhen, et al. A low-complexity ESPRIT-based DOA estimation method for co-prime linear arrays[J]. Sensors, 2016, 16(9): 1367. DOI:10.3390/s16091367 |
| [9] |
LI Jianfeng, JIANG Defu, ZHANG Xiaofei. DOA estimation based on combined unitary ESPRIT for coprime MIMO radar[J]. IEEE Communications Letters, 2017, 99: 1. |
| [10] |
ZHOU Chengwei, SHI Zhiguo, GU Yujie, et al. DECOM: DOA estimation with combined MUSIC for coprime array[C] // Wireless Communications & Signal Processing (WCSP). Hangzhou: IEEE Press, 2013: 119
|
| [11] |
LIU Chunlin, VAIDYNANTHAN P P. Remarks on the spatial smoothing step in coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438. |
| [12] |
THAKRE A, HAARDTM, GIRIDHAR K. Single snapshot spatial smoothing with improved effective array aperture[J]. IEEE Signal Processing Letters, 2009, 16(6): 505. |
| [13] |
SEKINE K, KIKUMA N, HIRAYAMA H, et al. DOA estimation using spatial smoothing with overlapped effective array aperture[C]//Microwave Conference Proceedings. New Delhi: IEEE press, 2013: 1100
|
| [14] |
IWAI T, HIROSE N, KIKUMA N, et al. DOA estimation by MUSIC algorithm using forward-backward spatial smoothing with overlapped and augmented arrays[C]// International Symposium on Antennas and Propagation. Vancouver: IEEE Press, 2015: 375
|
| [15] |
PAL P, VAIDYNANTHAN P P. Coprime sampling and the music algorithm[C]//Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop. Arizona: IEEE Press, 2011: 289
|
| [16] |
WAX M, ZISKIND I. On unique localization of multiple sources by passive sensor array[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 996. |
| [17] |
NEHORAI A, STARER D, STOICA P. Direction-of-arrival estimation in applications with multipath and few snapshots[J]. Circuits, Systems & Signal Processing, 1991, 10(3): 327. |
 2019, Vol. 51
2019, Vol. 51


