便携式落锤弯沉仪(portable falling weight deflectometer,PFWD)或称轻型落锤弯沉仪(light weight deflectometer,LWD),作为一种用于测量包括路基(单层体系)和基层(双层体系)刚度的快速无损检测仪器[1],研究其影响深度是确定PFWD配置参数与被检测对象相匹配的关键问题.
数值模拟方法采用有限元软件对PFWD的测试过程进行动态仿真模拟,分析不同影响因素对测试结果的影响[2-3].文献[4]利用刚性承载板中心下弹性半空间体z轴上的应力σz来分析落锤自由下落对土石填料产生的冲击影响深度.文献[5]通过室内填筑试验,研究LWD作用影响深度为267~280 mm.文献[6]在室内填筑的细粒土体中埋设土压力盒,结果表明落锤冲击能量70%消耗在40~50 cm土层内,该研究成果被写进了《铁路工程土工试验规程》[7]条文说明.以上无论是数值模拟还是试验研究,对于影响深度的定义不统一,不同的应力衰减程度(90%或70%)会有不同的影响深度结果,且没有考虑施加的荷载水平.对PFWD的影响深度的研究局限在标准配置下(板直径30 cm,锤质量为10 kg,某一固定高度使承载板底下产生应力集度0.1 MPa)的影响深度,而对组合配置下的影响深度少有研究.由于目前研究和应用主要针对单层结构的路基,其结果无法直接应用到公路工程中双层结构的底基层(基层)结构,为此需要研究双层结构下刚性承载板测定弯沉的应力衰减规律和影响深度,进而有针对性研究提出双层结构下PFWD检测试验配置参数,用于指导工程实际应用.
1 PFWD工作原理及动荷载特性分析 1.1 PFWD的工作原理在1981年德国马格德堡首先出现了携带方便的PFWD(LWD)[8],欧美市场上主要有德国ZORN ZFG型、HMP LFG型、丹麦PRIMA 100、芬兰Loadman型.前两类只有位移传感器,而后两类同时配备荷载和位移传感器,测量结果更全面可靠.
PFWD的基本原理是将某一重量的落锤提升至某一固定高度,然后释放让其自由下落,落锤冲击置放在路基(或路面)表面的承载板及底座上产生冲击荷载,在冲击荷载作用下,路基(或路面)表面产生竖向位移.由此,压力传感器和位移传感器将荷载和位移的时程数据记录下来,计算动态变形模量Evd的公式为
| $ {E_{{\rm{vd}}}} = \frac{{f\left( {1 - {\mu ^2}} \right)\sigma a}}{d}. $ |
式中:Evd为动态变形模量,MPa;μ为泊松比,μ=0.35(默认);σ为荷载板下的动应力峰值,MPa;a为承载板半径,mm;d为实测承载板中心位移峰值,mm;f为应力分布系数,均布荷载f=2(默认),刚性荷载f=π/2.
动态变形模量Evd是指土体在一定大小的竖向冲击力Fs和冲击时间ts作用下抵抗变形能力的参数,是90年代德国提出的路基压实质量控制标准.尽管PFWD是动力加载,反算模量时应当按照动力参数反算,文献[9]通过动静反算对比表明,PFWD实测的动、静模量基本一致.
1.2 动荷载特性分析为了进一步了解PFWD冲击荷载的产生原理,对其荷载施加装置的作用原理进行简化,如图 1所示.

|
图 1 PFWD作用原理 Fig. 1 Action principle of PFWD |
图中m为落锤的质量,h为下落的高度,k为弹簧的弹性常数,x为弹簧压缩量,由文献[10]可知PFWD产生的最大荷载为
| $ {F_{\max }} = k{x_{\max }} = \sqrt {2kmgh} . $ |
综上可见,影响PFWD动荷载的主要是锤重m,落高h和缓冲弹簧(橡胶)的弹性系数k,可合理地选择这些参数,以实现针对不同的路基、路面工况施加不同的荷载,已知PFWD在锤重10 kg,落高72.5 cm,承载板半径15 cm时,产生0.1 MPa的最大荷载,若假定弹性系数k一定,则其他配置下板下荷载为
| $ p = 0.1\sqrt {\frac{{mh}}{{725}}} \frac{{{{15}^2}}}{{{\delta ^2}}}. $ | (1) |
式中:p为最大荷载,p=Fmax/(πδ2),MPa;m为锤重,kg;h为落高,cm;δ为板半径,cm.
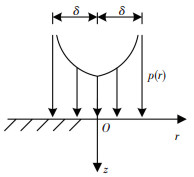
2 单层结构应力衰减分析 2.1 单层结构中竖向应力解对PFWD的应用研究,国内一般局限在路基检测中,路面力学分析中,路基往往视为单层结构. PFWD直接以刚性承载板作用于路基表面,通过落锤的冲击作用使得路基表面产生弯沉,所以用PFWD进行检测时,理论模型可采用刚性承载板下的弹性半空间体模型,如图 2所示.
|
图 2 刚性承载板荷载示意图 Fig. 2 Schematic diagram of rigid bearing plate load |
图 2中以板中心为原点O,经过原点竖直向下为z轴,板径向为r轴,刚性承载板下的压应力为
| $ p(r) = \left\{ {\begin{array}{*{20}{l}} {\frac{p}{2}\frac{1}{{\sqrt {1 - \frac{{{r^2}}}{{{\delta ^2}}}} }}, r < \delta ;}\\ {0, r > \delta } \end{array}} \right. $ |
式中p(r)为压应力.
由文献[11]可知刚性承载板下弹性半空间体对称轴(z轴)上竖向应力σz解析解为
| $ {\sigma _{z, r = 0}} = - \frac{p}{2}\frac{{1 + 3\frac{{{z^2}}}{{{\delta ^2}}}}}{{{{\left( {1 + \frac{{{z^2}}}{{{\delta ^2}}}} \right)}^2}}}. $ | (2) |
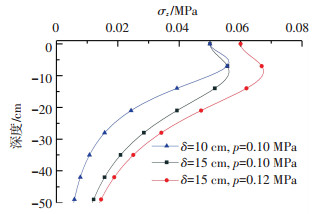
从式(2)中可以看出,对于单层结构,对称轴上竖向应力只与荷载大小、板半径和深度有关,图 3为不同板半径和不同平均荷载集度下板底中心处的竖向应力曲线.
|
图 3 不同板半径δ和不同荷载平均集度p下板底中心竖向应力曲线 Fig. 3 Vertical stress curves at the bottom under different plate radii and loads |
从图 3可以看出,板中心处竖向应力沿着深度方向均是先增加后减小,z=0和z=δ处竖向应力均为-p/2.同一板半径,荷载越大,竖向应力曲线右移,曲线形式是相似的,如δ=15 cm的两条曲线;对于相同荷载,半径越小,σz减小更快,如p=0.10 MPa的两条曲线.
2.2 应力余量应用PFWD对单层结构(路基)进行检测时,其测试深度即落锤自由下落对其产生的冲击影响深度,是需要考虑的一个重要问题.利用刚性承载板中心下弹性半空间体z轴上的应力σz来分析落锤自由下落对路基产生的冲击影响深度,从式(2)可知荷载p变化时,σz的曲线形式总是相似的.定义应力余量θ为刚性承载板中心下弹性体z轴上的应力σz与表面中心处(即O点)的应力之比,即
| $ \theta = \frac{{{\sigma _{z, r = 0}}}}{{{\sigma _{z = 0, r = 0}}}} \times 100\% . $ | (3) |
由式(2)、(3)得到,弹性半空间体对称轴上应力余量θ为
| $ \theta = \frac{{1 + 3\frac{{{z^2}}}{{{\delta ^2}}}}}{{{{\left( {1 + \frac{{{z^2}}}{{{\delta ^2}}}} \right)}^2}}} \times 100\% . $ | (4) |
这样仅需要研究θ,便可知σz的深度分布,由式(4)可以反算出影响深度z, 计算公式为
| $ \frac{z}{\delta } = \sqrt {\frac{{3 - 2\theta + \sqrt {9 - 8\theta } }}{{2\theta }}} . $ |
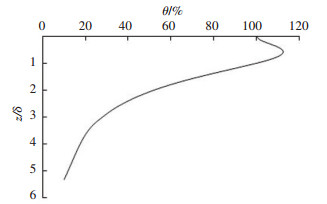
由此可见,应力余量θ只取决于深度与板半径相对大小z/δ,如θ=30%,即衰减70%,此时z=2.88δ;若θ=10%,即衰减90%,此时z=5.32δ. 图 4为半空间体(单层)θ与z/δ的关系曲线.
|
图 4 应力余量θ与z/δ的关系 Fig. 4 Relationship between θ and z/δ |
从图 4中看出,竖向应力必然遵循这样的衰减规律:并不是自板底(z=0)沿着深度方向一直单调衰减,而是在厚度为0~δ时,应力是一个先增加后减小的过程,此后在z=δ时,竖向应力的大小与板底中心竖向应力相等,而后是沿着深度方向一直衰减,图 4描述了半空间体任意荷载,任意板半径作用下对称轴上的竖向应力衰减规律.
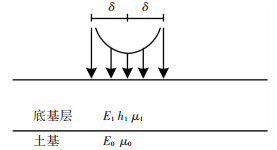
3 双层结构应力衰减分析应用PFWD对底基层(基层)进行试验检测时,此时路面力学模型对应为双层结构,如图 5所示.层与层在泊松比、模量存在差异,因而应力衰减必然要考虑到这些参数的影响.对于多层结构,不能用初等函数表示出应力分量解析解,为此需要通过COMSOL软件建立模型进行因素影响分析.
|
图 5 刚性荷载作用下双层结构示意图 Fig. 5 Schematic diagram of double-layer structure under rigid load |
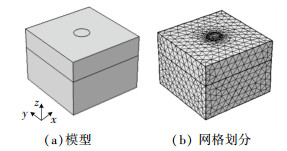
建立路面三维实体模型,图 6为模型及网格划分.荷载圆位于表面中心位置,半径用δ表示,荷载集度用p表示,模型尺寸为10δ×10δ×Hi的长方体,分为两层,其中i=0或1,i=0代表下承层,i=1代表检测层,两层结构材料模量、泊松比分别用Ei、μi表示,层间设为连续接触,下层底为固定约束,四周均为辊轴约束.
|
图 6 模型及网格划分 Fig. 6 Model and mesh |
当PFWD用于半刚性基层压实质量控制时,新摊铺的混合料铺筑在路基之上,刚压实完毕的模量(刚度)尚处于一个低水平,随着养生开始,刚度迅速增长,7 d养生后模量会增长10~20倍.对于双层结构,由于上下层模量、泊松比往往不同,尤其是模量变化大,需要研究其对应力衰减的影响。本节模型设定δ=15 cm,p=0.1 MPa,H0=1.5 m,H1=2δ=30 cm,μ0=μ1=0.35。
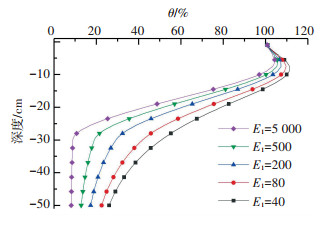
3.2.1 上层模量对应力衰减的影响设定下层模量E0=40 MPa,上层模量E1=40~5 000 MPa,以此研究随着半刚性基层模量的增长,应力衰减程度的变化规律,分析结果如图 7所示.从中可以看出,以上、下层模量相等(E1=E0)时作为参考,当上层模量大于下层模量时(E1> E0),衰减曲线向左偏移,即加速衰减,体现了半刚性基层扩散应力的作用,半刚性基层从摊铺压实至养生期结束,正是模量从低水平增长到高水平的过程,这期间下层(路基)模量基本稳定,上下层之间的模量存在显著差异,因而PFWD用于压实质量检测与养生结束后板体质量检测时的影响深度必然不同.
|
图 7 上层模量E1对竖向应力衰减的影响(E1≥E0) Fig. 7 Effect of upper layer modulus E1 on vertical stress (E1≥E0) |
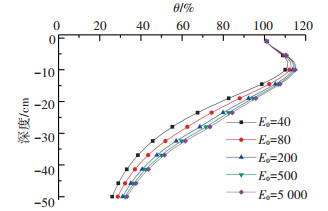
以上分析均是假定下层为路基,因此模量很小且变化不大,而工程中底基层施工验收合格后,便是基层施工,或是基层分层铺筑,下层对应就是下基层.这样下层模量(刚度)就会处在较高水平且变化较大.为模拟材料铺筑在不同结构层之上,设上层模量E1=40 MPa(表征压实完毕后的基层),下层模量E0=40~5 000 MPa,以此研究下层刚度变化对应力衰减程度的影响,分析结果如图 8所示.
|
图 8 下层模量E0对竖向应力衰减的影响(E1≤E0) Fig. 8 Effect of underlying layer modulus E0 on vertical stress (E1≤E0) |
从图 8可见,以上、下层模量相等时(E0=E1)作为参考,随着下层模量的增长,衰减曲线向右偏移,即延缓衰减,表明下承层刚度越大,层底竖向应力越大,PFWD落锤作用影响深度会变大,表明随着道路施工层位越来越高,对于底基层与基层压实质量控制的PFWD影响深度也不同.
3.2.3 相对模量对应力衰减的影响从以上单变量的分析可见,应力衰减是与上下层相对模量大小有关的,为此设定不同的上下层模量比E1/E0和不同的层厚H1/δ,计算上层层底(z=-H1)的竖向应力σz,研究不同模量比对层底应力余量θ的影响规律,模型计算结果如图 9所示.

|
图 9 双层结构下应力余量θ计算图 Fig. 9 Calculation of θ under double-layer structure |
图 9为不同层厚H1/δ下应力余量θ随模量比E1/E0的衰减曲线.整体上看,对于特定的层厚,随着E1/E0的增大,应力余量θ逐渐减小;对于特定的E1/E0,随着层厚的增加,应力余量也随之减小.
当E1/E0=1时,即模型退化为单层结构,H1/δ=1时,模型计算结果θ=97%,而将z/δ=-H1/δ=-1代入式(4),得单层结构的理论应力余量θ=100%,模型计算结果与理论接近,只有3%的偏差.同样当H1/δ=2时,模型计算结果θ=49%,理论应力余量θ=52%,模型计算结果与理论很接近,模型计算结果可以满足工程应用需要.
3.3 泊松比对应力衰减的影响以上分析中,均是假定上下层泊松比是相等的,工程实际中,基层材料往往采用半刚性材料,泊松比的变化范围很小.为研究泊松比对衰减的影响,图 10为不同泊松比的竖向应力衰减曲线(H1=30 cm,δ=15 cm,E0=40 MPa,E1=500 MPa,μ0=0.4).

|
图 10 泊松比μ对竖向应力衰减的影响 Fig. 10 Influence of Poisson's ratio on vertical stress |
从中可以看出,检测层的泊松比在0.25~0.40之间变化时,竖向应力衰减曲线几乎重合在一起,即泊松比对应力衰减影响极小,在实际工程应用中可以忽略不计.
4 影响深度分析铁路路基领域研究者通过在土体不同深度中埋设压力盒试验研究PFWD的影响深度[6],其施加承载板板下荷载集度固定为0.1 MPa(该值被认为是列车高速运行时对路基产生的最大动应力),以应力衰减70%的深度作为影响深度,则影响深度为40 cm左右[7, 12-13],满足路基施工中填土每碾压30 cm厚度检测一次的要求.铁路领域应用的PFWD一般是ZFG或LFG型,采用标准配置:直径为30 cm承载板,落锤10 kg,下落高度固定约72.5 cm.
在道路工程领域中,目前很多研究者将其用在路基压实质量检测中,采用标准配置时,其影响深度均沿用铁路领域中的规定.当将PFWD应用到(底)基层检测中,力学模型变为双层结构,上下层存在模量差异,表面施加的荷载水平自然要随之改变.同时,施加不同的荷载水平必然产生不同的影响深度.考虑表面施加的荷载水平不同,若仍按照应力衰减百分比定义影响深度显然是不准确的,相同的衰减百分比,施加的荷载不同,影响深度不同,应当以应力衰减至某一绝对水平来定义影响深度.铁路路基领域中以应力衰减70%,即对称轴z轴上的竖向应力从0.05 MPa衰减至0.015 MPa的深度为影响深度,为保持与路基检测影响深度一致,本研究规定对称轴z轴竖向应力衰减至0.015 MPa时的深度为影响深度.
本研究所用的PRIMA 100配备有10 kg和15 kg重锤,承载板有直径10、20、30 cm可选,通过改变PFWD的配置(锤重、板半径组合)即可施加不同大小的表面荷载p,板底中心竖向应力沿着深度向下衰减,令竖向应力衰减至0.015 MPa可计算出该配置下的荷载影响深度. 表 1为计算得到的PFWD不同配置下的道路结构层(基层)影响深度.
| 表 1 PFWD检测影响深度 Tab. 1 Action depth of PFWD |
计算过程分3步:1)确定施加荷载水平;2)确定影响深度所对应的应力余量值;3)结合E1/E0的值,从图 9中读取影响深度值,比如:当板半径δ=15 cm,锤重m=15 kg,代入式(1)得p=0.122 MPa,θ=0.015/(0.122/2)=24.5%,若E1/E0=2,查图 9可知交点处于H1/δ=2.6~2.8,即H1=39~42 cm,以此类推.
5 PFWD参数配置影响PFWD测量结果的配置参数有锤重、落高、承载板尺寸,最显著的因素是承载板尺寸和锤重,而落锤高度对PFWD模量影响很小可忽略.此外还有承载板与材料层之间的接触,良好接触才能确保测试结果的准确[14-15].在实际中频繁改变高度不利于维持稳定的荷载水平,且高度对检测的模量值影响不大,将落锤高度固定为72.5 cm不变,且仅通过改变锤重和承载板尺寸来施加不同荷载水平. 10 cm的承载板尺寸过小,基层混合料公称最大粒径一般为26.5~31.5 mm,此接触面积不具代表性,而且操作中一旦落锤提升,重心过高不利于设备保持平稳放置,影响测量准确性,因而只推荐选用20 cm以上的承载板.
PFWD应用广泛的领域之一就是压实质量控制,目前研究和应用主要针对单层结构的路基,其结果无法直接应用到公路工程中双层结构的底基层(基层)结构,以下分类论述不同工况下配置参数选择.
1) 路基土上摊铺底基层时(压实未养生),此时水稳底基层模量接近或稍高于下承层(路基土)模量,层厚度为20~30 cm,结合表 1的影响深度,采用标准配置即可(锤重10 kg,30 cm承载板).
2) 底基层上新铺压实未养生的基层,下层的底基层和路基,可视为整体复合模量接近底基层的单层,新铺层刚度远低于下承层的刚度(E1/E0 < 1),且压实未养生层刚度还处于低水平,为了防止荷载水平过大或材料含水量过大产生塑性变形,同时考虑到摊铺层厚度在20~30 cm,标准配置即可满足.
3) 对于养生7 d后的底基层板体刚度检测,底基层模量相较路基大很多,上下层模量比E1/E0处在5~10之间,小尺寸承载板与底基层顶面可以更容易紧密接触,提高检测结果的准确可靠性,推荐锤重10 kg和20 cm承载板组合,而对于养生7 d后的基层板体刚度检测,该组合配置仍可满足.
综上分析,PFWD主要应用于基层压实质量控制和板体刚度检测两方面,配置锤重10 kg,对应的承载板直径分别为30 cm和20 cm.
6 结论1) 定义应力余量θ为刚性承载板对称轴(z轴)上的应力σz与表面中心处(即σz=0)的应力之比,单层结构中应力衰减程度的大小只取决于深度与板半径相对大小z/δ,双层结构中还取决于模量比E1/E0,但与表面施加的荷载大小无关.
2) 荷载中心处的竖向应力σz, 并不是自板底(z=0)沿着深度方向一直单调衰减,而是在厚度为0~δ时,应力σz是一个先增加后减小的过程,此后在z=δ时,竖向应力的大小与z=0的竖向应力相等,此后是沿着深度方向一直衰减.
3) 以对称轴竖向应力衰减至0.015 MPa时的厚度作为影响深度,计算出了不同PFWD配置下的基层结构适宜检测深度,结合工程实际推荐了配置参数组合,用于新铺层检测推荐锤重10 kg和30 cm承载板,养生7 d后的底基层(基层)的刚度检测,推荐锤重10 kg和20 cm承载板.
| [1] |
STEINERT B C, HUMPHREY D N, KESTLER M A. Portable falling weight deflectometer study: NETCR52[R]. Maine: University of Maine, 2005
|
| [2] |
周文. PFWD测试工作特性仿真研究[J]. 公路工程, 2009, 34(6): 112. ZHOU Wen. Research on PFWD simulation technology[J]. Highway Engineering, 2009, 34(6): 112. DOI:10.3969/j.issn.1674-0610.2009.06.027 |
| [3] |
李跃军.路基强度的快速无损检测、评价与控制研究[D].长沙: 中南大学, 2011 LI Yuejun. Research on rapid nondestructive detection, evaluation and control of subgrade strength[D]. Changsha: Central South University, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10533-1012474083.htm |
| [4] |
王复明, 渠建伟, 王运生. 便携式落锤弯沉仪PFWD在土石填料压实质量控制中的应用[J]. 铁道建筑, 2008, 415(9): 67. WANG Fuming, QU Jianwei, WANG Yunsheng. Application of PFWD (portable falling weight deflectometor) to quality control over compactness of filled soil-stone[J]. Railway Engineering, 2008, 415(9): 67. DOI:10.3969/j.issn.1003-1995.2008.09.024 |
| [5] |
NAZZAL M D. Field evaluation of in-situ test technology for Qc/QA during construction of pavement layers and embankments[D]. Baton Rouge: Louisiana State University, 2003 https://www.researchgate.net/publication/234476024_Field_Evaluation_of_in-Situ_Test_Technology_for_QCQA_during_Construction_of_Pavement_Layers_and_Embankments
|
| [6] |
李怒放. DBM型动态变形模量测试仪的研制及其工程应用[D].成都: 西南交通大学, 2005 LI Nufang. The development of the measuring instrument for dynaminc deformation modulus and its application in engineering[D]. Chengdu: Southwest Jiaotong University, 2005 http://cdmd.cnki.com.cn/Article/CDMD-10613-2008038545.htm |
| [7] |
中华人民共和国铁道部.铁路工程土工试验规程: TB 10102-2010[S].北京: 中国铁道出版社, 2011: 423 Ministry of Railways of the People's Republic of China. Code for soil test of railway engineering: TB 10102-2010[S]. Beijing: China Railway Publishing House, 2011: 423 |
| [8] |
ELHAKIM A F, ELBAZ K, AMER M I. The use of light weight deflectometer for in situ evaluation of sand degree of compaction[J]. HBRC Journal, 2014, 10(3): 298. |
| [9] |
查旭东, 袁盛杰, 肖秋明. 冲击荷载作用下的路基动力反算[J]. 长沙理工大学学报, 2014, 11(4): 1. ZHA Xudong, YUAN Shengjie, XIAO Qiuming. Subgrade dynamic backcalculation under impact loading[J]. Journal of Changsha University of Science and Technology (Natural Science), 2014, 11(4): 1. DOI:10.3969/j.issn.1672-9331.2014.04.001 |
| [10] |
唐伯明, 李锦华, 谭忠明. PHONIX FWD量测性能评价[J]. 华东公路, 1995, 6: 24. TANG Boming, LI Jinhua, TAN Zhongming. Evaluation of PHONIX FWD measurement performance[J]. East China Highway, 1995, 6: 24. |
| [11] |
郭大智. 层状弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001: 64. GUO Dazhi. Layered elastic system mechanics[M]. Harbin: Harbin Institute of Technology Press, 2001: 64. |
| [12] |
Road and Transportation Research Association.Supplementary technical terms and conditions of contract and guidelines for earthworks in road construction: ZTVE-StB 94[S]. Cologne: Earthworks and Foundation Engineering Task Force, 1994
|
| [13] |
GEORGE V, KUMAR A. Studies on modulus of resilience using cyclic tri-axial test and correlations to PFWD, DCP, and CBR[J]. International Journal of Pavement Engineering, 2018, 19(11): 976. |
| [14] |
STAMP D H, MOONEY M A. Influence of lightweight deflectometer characteristics on deflection measurement[J]. Geotechnical Testing Journal, 2013, 36(2): 216. |
| [15] |
MAKWANA P. Structural evaluation and quality assurance of flexible pavement using light weight deflectometer[J]. Journal of Civil & Structural Engineering, 2016, 6(3): 160. |
 2019, Vol. 51
2019, Vol. 51


