2. 吉林大学 汽车工程学院,长春 130022
2. College of Automotive Engineering, Jilin University, Changchun 130022, China
驾驶员安全辅助、安全预防和安全管理等技术是智能交通研究的重点.由于驾驶员存在生理、心理局限性,易出现由于对行驶环境感知不明、驾驶疲劳等导致的误判、误操作等行为,从而导致交通事故.而过街行人,由于缺乏相关的保护措施,更易受到道路事故的伤害[1-2].车路协同(cooperative vehicle infrastructure system, CVIS)技术为准确的行人碰撞风险识别和预警提供了可能.
CVIS环境下行人碰撞规避研究一直受到学者们的关注.文献[3]提出了一种基于车路协同与机器视觉的行人防碰撞系统.文献[4]提出了基于Wi-Fi系统检测的行人防碰碰预警系统.文献[5]比较了在IEEE 802.11p和WiFi通讯环境下的行人检测范围.对于驾驶员主动避碰驾驶方法的研究,文献[6]提出了一种基于人工势场的车辆换道避碰算法.文献[7]建立了基于总相对动能密度最小的车队协同避碰算法.文献[8]基于概率导航函数对碰碰风险分析进行识别,并实例验证了行人过街路径规划行为.文献[9]考虑了行人对车辆的安全避碰距离,采用泰森多边形法分析了行人流特征.从现有的研究来看,对行人碰撞的规避,学者们主要关注于行人检测及危险预警,而对车辆如何进行避障驾驶关注的较少;现有的避碰算法以车队纵向避碰为主,对于车辆换道等横向避碰算法的研究不多.
本文基于速度障碍法(velocity obstacle,VO)的基本原理,将过街行人视为速度障碍,提出一种在CVIS环境下的车辆对行人自主避碰的模型预测控制(model predictive control, MPC)算法,以期在降低驾驶人对行人的碰撞风险的同时提高车辆的运行效率.
1 速度障碍模型速度障碍理论是由文献[10]提出的一种与运动中的障碍物避碰的算法,广泛应用于机器人路径规划中.文献[11]基于速度障碍圆弧法对自动飞行器的主动避障路径进行规划.文献[12]将速度障碍法应用于非直线运动的船舶的避障研究中.速度障碍法目前在城市交通领域的应用还不多见.文献[13]构建了基于速度障碍的结伴行人运动模型.与机器人相比,行人的行为具有主观性,不容易受到约束,因此在车辆与行人的碰撞规避中更应该把重点放置于对车辆驾驶的操作控制.
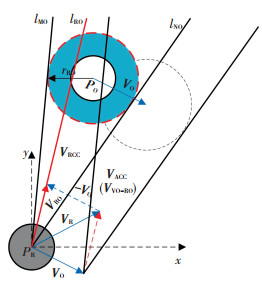
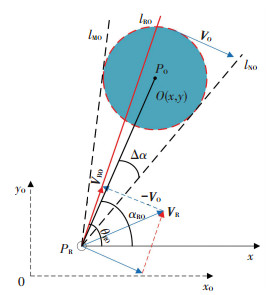
1.1 障碍锥将某一移动物体表示为R,在此为机动车,障碍物用O表示,在此为行人.其半径分别为rR与rO.根据车辆和障碍物之间的相对尺寸大小对已知障碍物O进行“膨化”处理,“膨化”后的区域记作PO,其圆半径记作rRO=rR+rO. 图 1为障碍物对车辆所产生的速度障碍锥示意图,图 2为速度障碍的表达,射线lMO和lNO为车辆至障碍圆的两条切线. PO与PR分别为车辆与行人的位置,VO与VR为车辆与行人的车速.
|
图 1 速度障碍示意图 Fig. 1 Schematic of velocity obstacle |
|
图 2 速度障碍表达 Fig. 2 Representation of velocity obstacle |
障碍物O与车辆R之间的相对速度为VRO= VR- VO,若将O视为静止,那么此时的场景即相当于一辆车速为VRO的机动车沿着lRO方向向障碍物O行驶,基于障碍锥(collision cone)的概念,当车辆与障碍物的相对速度矢量位于障碍锥内时,则该障碍物属于威胁障碍.即将发生碰撞的条件描述为
| $ {\mathit{\boldsymbol{V}}_{{\rm{RCC}}}} = \left\{ {{\mathit{\boldsymbol{V}}_{{\rm{RO}}}}|{l_{{\rm{RO}}}} \cap {P_{\rm{O}}} \ne \phi } \right\}, $ |
其中VRCC为VRO的速度集合,即图 1中射线lMO与lNO围成的锥形区域,若VRO∈ VRCC,则R将与O发生碰撞.
1.2 速度障碍将示意图 1中速度障碍锥沿障碍物的速度矢量VO方向平移,得到绝对速度障碍锥VACC(absolute collision cone).其中VACC= VRCC⊕VO,⊕为闵可夫斯基运算符.基于二维平面速度障碍法原理,车辆R的速度VR末端点位于VACC等同于VRO位于VRCC,将所有末端点位于VACC的车速VR用VRnew表示,即由行人O移动而导致的车辆R的速度障碍描述为
| $ {\mathit{\boldsymbol{V}}_{{\rm{VO - RO}}}}\left( {{\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) = \left\{ {{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}}|\left( {{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}} - {\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) \in {\mathit{\boldsymbol{V}}_{{\rm{RCC}}}}} \right\}. $ |
为了克服上述算法在个体避让障碍物时出现的震荡现象,速度障碍原理提出了互动速度障碍的概念.如果R选择的新的相对速度VROnew= VRnew- VO等于当前相对速度VRO和任意一个位于VRCC范围之外的速度的平均值,称这个互惠的速度障碍为互动速度障碍(interactive velocity obstacle,IVO).个体选择的碰撞速度矢量V-Rnew′符合关系式:
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{\rm{IVO}} - {\rm{RO}}}}\left( {{\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) = \left\{ {\mathit{\boldsymbol{V}}_{ - {\rm{Rnew}}}^\prime |\mathit{\boldsymbol{V}}_{ - {\rm{Rnew}}}^\prime - {\mathit{\boldsymbol{V}}_0} = \frac{{{\mathit{\boldsymbol{V}}_{{\rm{RO}}}} + {\mathit{\boldsymbol{V}}_{{\rm{ROany}}}}}}{2},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{V}}_{{\rm{ROany}}}} \in {\mathit{\boldsymbol{V}}_{{\rm{RCC}}}}} \right\}, \end{array} $ |
其等价形式为
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{\rm{IVO}} - {\rm{RO}}}}\left( {{\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) = \left\{ {\mathit{\boldsymbol{V}}_{ - {\rm{Rnew}}}^\prime |2\mathit{\boldsymbol{V}}_{ - {\rm{Rnew}}}^\prime - {\mathit{\boldsymbol{V}}_{\rm{R}}} - {\mathit{\boldsymbol{V}}_{\rm{O}}} \in {\mathit{\boldsymbol{V}}_{{\rm{RCC}}}}} \right\},即\\ 2\mathit{\boldsymbol{V}}_{ - {\rm{Rnew}}}^\prime - {\mathit{\boldsymbol{V}}_{\rm{R}}} \in {\mathit{\boldsymbol{V}}_{{\rm{VO - RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right). \end{array} $ |
对于R来说,需要进一步考虑优先的互让方向,即比较VROnew、VRO、PO-PR的关系,如果VROnew与VRO的方向位于PO-PR的同一侧,可采用VIVO-RO(vO)作为速度障碍.相反的,如果VROnew与VRO的方向分别位于PO-PR的同一侧,可采用VIVO-RO(vO)作为速度障碍[14].其中αRO=∠(PO-PR),θRO为VRO与x轴的夹角,θROnew是VROnew与x轴的夹角.综上,将此复合速度障碍定义为
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{\rm{HIVO - RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right) = \\ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_{{\rm{VO - RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right),\left( {{\theta _{{\rm{ROnew}}}} - {\alpha _{{\rm{RO}}}}} \right)\left( {{\theta _{{\rm{RO}}}} - {\alpha _{{\rm{RO}}}}} \right) \le 0;}\\ {{\mathit{\boldsymbol{V}}_{{\rm{IVO}} - {\rm{RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right),\left( {{\theta _{{\rm{ROnew}}}} - {\alpha _{{\rm{RO}}}}} \right)\left( {{\theta _{{\rm{RO}}}} - {\alpha _{{\rm{RO}}}}} \right) > 0.} \end{array}} \right. \end{array} $ |
本文通过相对速度矢量VRO之间的夹角差(θRO-αRO)与障碍锥的半顶角Δα大小关系进行障碍威胁判断.
基于速度障碍的判定方法,当满足下式时,两个移动物体之间存在碰撞风险,表明O对R构成威胁,即
| $ - \Delta \alpha < \left( {{\theta _{{\rm{RO}}}} - {\alpha _{{\rm{RO}}}}} \right) < \Delta \alpha , $ | (1) |
由此得到速度障碍的判定方法为
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{\rm{VO - RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right) = \left\{ {{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}}| - \Delta \alpha < \angle \left( {{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}} - {\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\alpha _{{\rm{RO}}}} < \Delta \alpha } \right\}, \end{array} $ | (2) |
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{\rm{IVO}} - {\rm{RO}}}}\left( {{\mathit{\boldsymbol{v}}_{\rm{O}}}} \right) = \left\{ {{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}}| - \Delta \alpha < \angle \left( {2{\mathit{\boldsymbol{V}}_{{\rm{Rnew}}}} - {\mathit{\boldsymbol{V}}_{\rm{R}}} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{\mathit{\boldsymbol{V}}_{\rm{O}}}} \right) - {\alpha _{{\rm{RO}}}} < \Delta \alpha } \right\}. \end{array} $ | (3) |
在CVIS环境下,障碍物(行人)的位置PO(xO, yO)和速度矢量VO(vOx, vOy)信息可通过路侧设备采集,并通过无线网络实时传输给机动车.此时机动车可根据其当前与行人的相对位置及相对速度关系,对碰撞风险进行评估,并且可以通过评估结果对风险进行规避.
2 基于行人识别的智能车辆自主避碰控制器设计智能车辆自主避碰控制器的核心模块,如图 3所示,由3部分组成:1)由路侧设备采集过街行人的运动信息,并通过通信手段传输给车辆.车载传感器采集车辆状态信息.车辆的信息处理设备处理采集得到的行人与车辆的位置信息. 2)车辆的模型预测控制器通过对信息流输入量进行响应,实施车辆跟驰与换道策略的选择和切换,确保车辆在当前状态和环境下的控制目标以及满足相应的约束条件.3)控制算法通过动态改变相应的控制目标与约束条件得到车辆执行机构或车辆模型所需要的控制量输入,从而完成车辆的自主避碰控制.

|
图 3 智能车辆自主避碰控制器框架 Fig. 3 Framework of autonomous collision avoidance controller for intelligent vehicles |
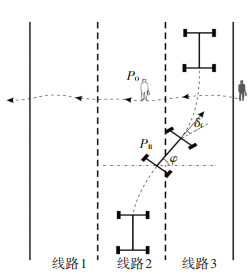
为了检验本文所设计控制器对行人避碰的控制效果.在此设计两个控制场景:一是机动车受到道路上其他车辆的限制,不能自由换道,车辆采取速度控制策略对行人进行避让,在当前车道上加速或减速;二是机动车可以自由换道.当车辆检测到过街行人时除了直行速度控制外,车辆还可以采用换道控制策略进行避让,将由控制目标的优化结果进行最终操作决策.依据判断车辆换道至相邻车道行驶的可行性,车辆可以在向左或向右换道进行选择.如图 4描述了车辆向右侧换道对行人进行碰撞规避的情形,当行人走行至PO位置时,车辆向右侧换道至PR.
|
图 4 车辆右侧换道避碰行人 Fig. 4 Right lane change behavior of vehicle to avoid collision for pedestrians |
本文提出的模型预测控制器采用的车辆运动学模型.在地面固定坐标系OXY下,车辆运动学方程为ζ · = x ·
| $ \dot \zeta = \left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot \varphi } \end{array}} \right] = \left[ \begin{array}{l} \cos \varphi \\ \sin \varphi \\ \tan {\delta _{\rm{f}}}/l \end{array} \right] \cdot v. $ | (4) |
式中:(x, y)为车辆后轴中心坐标,φ为车辆航向角,δf为车辆前轮偏角,v为车辆后轴速度,l为轴距,通常为2.5~2.7 m.
设T为离散时间的一个步长,则得到离散化的车辆运动学模型为
| $ \begin{array}{l} \zeta \left( {n + 1} \right) = \left[ {\begin{array}{*{20}{l}} {x\left( {n + 1} \right)}\\ {y\left( {n + 1} \right)}\\ {\varphi \left( {n + 1} \right)}\\ {v\left( {n + 1} \right)}\\ {\delta \left( {n + 1} \right)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {x(n) + T \cdot v(n)\cos (\varphi (n))}\\ {y(n) + T \cdot v(n)\sin (\varphi (n))}\\ {\varphi (n) + T \cdot v(n)/(l \cdot \tan (\delta (n))}\\ {v(n) + \Delta v(n)}\\ {\delta (n) + \Delta \delta (n))} \end{array}} \right]. \end{array} $ | (5) |
式中:Δv为车辆的加/减速度,Δδ为车轮偏转角增量.
模型预测控制器第n步的输入量为Δu(n)=[Δv(n), Δδ(n)]T,车辆随着控制变量的变化而改变方向与速度.
3.2 车辆控制模型建立 3.2.1 控制目标模型优化目标是在机动车对行人碰撞风险规避的前提下使得车辆速度变化最小同时满足驾驶员操作的舒适性.对于换道行为,舒适性体现在车辆转向角不要变化太大.确定控制目标函数为
| $ \min J = \sum\nolimits_{i = 1}^n {{{\left\| {\Delta u\left( {{t_i}} \right)} \right\|}^2}} , $ | (6) |
其中ti为第i个时间步,n为时间步的数量.
3.2.2 约束条件1) 位置关系约束.基于车辆的运动关系,车辆的加速度、速度、位移之间的关系满足如下关系式.
速度约束为
| $ {V_{\rm{R}}}\left( {{t_i}} \right) = {V_R}\left( {{t_{i - 1}}} \right) + {u_{\rm{R}}}\left( {{t_{i - 1}}} \right) \cdot T, $ | (7) |
| $ \delta \left( {{t_i}} \right) = \delta \left( {{t_{i - 1}}} \right) + \Delta \delta \left( {{t_{i - 1}}} \right) \cdot T, $ | (8) |
| $ \varphi \left( {{t_i}} \right) = \varphi \left( {{t_{i - 1}}} \right) + \frac{{{V_{\rm{R}}}\left( {{t_{i - 1}}} \right)}}{l}\tan \left( {\delta \left( {{t_{i - 1}}} \right)} \right) \cdot T. $ | (9) |
位移约束为
| $ {y_{\rm{R}}}\left( {{t_i}} \right) = {y_{\rm{R}}}\left( {{t_{i - 1}}} \right) + {V_{\rm{R}}}\left( {{t_{i - 1}}} \right) \cdot T \cdot \sin \left( {\varphi \left( {{t_{i - 1}}} \right)} \right), $ | (10) |
| $ {x_{\rm{R}}}\left( {{t_i}} \right) = {x_{\rm{R}}}\left( {{t_{i - 1}}} \right) + {V_{\rm{R}}}\left( {{t_{i - 1}}} \right) \cdot T \cdot \cos \left( {\varphi \left( {{t_{i - 1}}} \right)} \right). $ | (11) |
其中:VR(ti)为第i个时间步的车辆R的速度;uR(ti-1)为第i-1个时间步的车辆R的加速度;T为时间步长,通常取1 s;δ(ti)为第i个时间步的车辆前轮偏角;Δδ(ti-1)为第i-1个时间步的车辆前轮偏角角速度;φ(ti)为第i个时间步的车辆航向角;yR(ti)为第i个时间步的车辆R的y轴方向上的位移;xR(ti)为x轴方向上的位移.
车辆间的位置约束为当前车辆直行时与当前车道的前、后车满足最小车头间距;换道时,与相邻车道上的前、后车满足最小车头间距,即
| $ \int_i^{i + 1} {\left( {{V_{{\rm{Rfront}}}}(t) - {V_{\rm{R}}}(t)} \right){\rm{d}}t} \ge {G_{\min }}, $ | (12) |
| $ \int_i^{i + 1} {\left( {{V_{\rm{R}}}(t) - {V_{{\rm{Rback}}}}(t)} \right){\rm{d}}t} \ge {G_{\min }}, $ | (13) |
| $ \int_i^{i + 1} {\left( {{{V'}_{{\rm{Rfront}}}}(t) - {V_{\rm{R}}}(t)} \right){\rm{d}}t} \ge {G_{\min }}, $ | (14) |
| $ \int_i^{i + 1} {\left( {{V_{\rm{R}}}(t) - {{V'}_{{\rm{Rback}}}}(t)} \right){\rm{d}}t} \ge {G_{\min }}, $ | (15) |
其中:VRfront为当前车道上的前导车速度,VRback为当前车道后车的速度,VRfront′相邻车道上的前导车的速度,VRback′相邻车道上的后车的速度,Gmin为车辆间不碰撞所需保持的最小车头间距,i=1, 2, …, m,j=m+1, m+2, …, n.
2) 避碰条件.结合式(1)、(2)、(3)得到车辆的避碰约束为
| $ \left| {\arctan \left( {\frac{{{V_{{\rm{O}}y}}\left( {{t_{i - 1}}} \right) - {V_{\rm{R}}}\left( {{t_i}} \right)\sin \left( {\varphi \left( {{t_i}} \right)} \right)}}{{{V_{{\rm{O}}x}}\left( {{t_{i - 1}}} \right) - {V_{\rm{R}}}\left( {{t_i}} \right)\cos \left( {\varphi \left( {{t_i}} \right)} \right)}}} \right) - {\alpha _{{\rm{RO}}}}} \right| > \Delta \alpha , $ | (16) |
| $ \left| {\arctan \left( {\frac{{2{V_{\rm{R}}}\sin \left( {\varphi \left( {{t_i}} \right)} \right) - {V_{\rm{R}}}\left( {{t_{i - 1}}} \right)\sin \left( {\varphi \left( {{t_{i - 1}}} \right) - {V_{{\rm{O}}y}}\left( {{t_{i - 1}}} \right)} \right)}}{{2{V_{\rm{R}}}\cos \left( {\varphi \left( {{t_i}} \right)} \right) - {V_{\rm{R}}}\left( {{t_{i - 1}}} \right)\cos \left( {\varphi \left( {{t_{i - 1}}} \right) - {V_{{\rm{O}}x}}\left( {{t_{i - 1}}} \right)} \right)}}} \right) - {\alpha _{{\rm{RO}}}}} \right| > \Delta \alpha . $ | (17) |
| $ 其中:{\alpha _{{\rm{RO}}}} = \arctan \frac{{{y_{\rm{O}}}\left( {{t_i}} \right) - {y_{\rm{R}}}\left( {{t_i}} \right)}}{{{x_{\rm{O}}}\left( {{t_i}} \right) - {x_{\rm{R}}}\left( {{t_i}} \right)}}, $ | (18) |
| $ \Delta \alpha = \arcsin \frac{{{r_{{\rm{RO}}}}}}{{\sqrt {{{\left( {{y_{\rm{O}}}\left( {{t_i}} \right) - {y_{\rm{R}}}\left( {{t_i}} \right)} \right)}^2} + {{\left( {{x_{\rm{O}}}\left( {{t_i}} \right) - {x_{\rm{R}}}\left( {{t_i}} \right)} \right)}^2}} }}, $ | (19) |
| $ {\theta _{{\rm{RO}}}} = \arctan \frac{{{V_{\rm{R}}}\left( {{t_i}} \right)\sin \left( {\varphi \left( {{t_{i - 1}}} \right)} \right) - {V_{{\rm{O}}y}}\left( {{t_{i - 1}}} \right)}}{{{V_{\rm{R}}}\left( {{t_i}} \right)\cos \left( {\varphi \left( {{t_{i - 1}}} \right)} \right) - {V_{{\rm{O}}x}}\left( {{t_{i - 1}}} \right)}}, $ | (20) |
| $ {\theta _{{\rm{ROnew}}}} = \arctan \frac{{{V_{\rm{R}}}\left( {{t_i}} \right)\sin \left( {\varphi \left( {{t_i}} \right)} \right) - {V_{{\rm{O}}y}}\left( {{t_{i - 1}}} \right)}}{{{V_{\rm{R}}}\left( {{t_i}} \right)\cos \left( {\varphi \left( {{t_i}} \right)} \right) - {V_{{\rm{O}}x}}\left( {{t_{i - 1}}} \right)}}. $ | (21) |
式中:yO(ti)、xO(ti)为第i个时间步行人的y轴、x轴方向上的位移;VOy、VOx(ti-1)为第i-1个时间步行人的y轴、x轴方向上的速度.在模型中,这4个参数为已知数据,通过路侧设备检测获得.
3) 参数取值约束.为保证优化结果符合实际情况,同时使得智能车辆驾驶过程更加平稳,需要设置相应的约束条件为
| $ {\mu _{\min }} \le \mu \left( {{t_i}} \right) \le {\mu _{\max }}, $ | (22) |
| $ 0 \le {V_{\rm{R}}}\left( {{t_i}} \right) \le {V_{{\rm{Rmax}}}}. $ | (23) |
其中μmax、VRmax分别为车辆最大的加/减速度与速度约束.
在横向控制中,考虑到机动车转向的实际操作可能,将车辆车轮偏角增量约束、航向角约束设置为
| $ - {9.4^\circ }/{\rm{s}} < \Delta \delta \left( {{t_i}} \right) < {9.4^\circ }/{\rm{s,}} $ | (24) |
| $ - {10^\circ } < \varphi \left( {{t_i}} \right) - \varphi \left( {{t_{i - 1}}} \right) < - {10^\circ }. $ | (25) |
4) 避碰决策约束分为以下3种情况.
直行避碰.当前车辆与相邻车道上的后车、前车的距离均小于最小车头间距,此时当前车辆采取直行避碰策略:
| $ {X_{\rm{R}}}\left( {{t_i}} \right) - X_{{\rm{Rback}}}^\prime \left( {{t_i}} \right) \le {G_{{\rm{min}}}}, $ | (26) |
| $ X_{{\rm{Rfront}}}^\prime \left( {{t_i}} \right) - {X_{\rm{R}}}\left( {{t_i}} \right) \le {G_{{\rm{min}}}}. $ | (27) |
其中:XR(ti)为第i个时间步当前车辆的位置,XRback′(ti)为第i个时间步相邻车道后车的位置,XRfront′(ti)为第i个时间步相邻车道前车的位置.换道避碰.当前车辆与当前车道上的后车、前车的距离均小于最小车头间距,且相邻车道上的前、后车均大于最小车头间距,存在换道空间.此时当前车辆采取换道策略:
| $ {X_{\rm{R}}}\left( {{t_i}} \right) - {X_{{\rm{Rback}}}}\left( {{t_i}} \right) \le {G_{{\rm{min}}}}, $ | (28) |
| $ {X_{{\rm{Rfront}}}}\left( {{t_i}} \right) - {X_{\rm{R}}}\left( {{t_i}} \right) \le {G_{{\rm{min}}}}. $ | (29) |
| $ {X_{\rm{R}}}\left( {{t_i}} \right) - {{X'}_{{\rm{Rback}}}}\left( {{t_i}} \right) \ge {G_{{\rm{min}}}}, $ | (30) |
| $ {{X'}_{{\rm{Rfront}}}}\left( {{t_i}} \right) - {X_{\rm{R}}}\left( {{t_i}} \right) \ge {G_{{\rm{min}}}}. $ | (31) |
其中XRback(ti)为第i个时间步当前车道后车的位置,XRfront(ti)为第i个时间步相邻车道前车的位置.
自主避碰.当前车辆与其他车辆的位置关系不满足式(26)~(31)时,当前车辆自主选择直行或是换道策略.
4 仿真场景验证为验证所提出的模型预测控制器的控制效果,在MATLAB环境中搭建仿真场景,设计不同的行人走行路径进行仿真实验.
rRO为一个空身的行人在人行横道活动时的活动圈半径,不同直径的活动圈对行人活动的影响是不同的.在此假设是单个行人,依据文献[15],取rRO=1.34 m.通常上述值反映的是行人与行人之间的舒适距离,在机动车与行人的交互过程中,行人通常会要求更大的心理安全距离,根据问卷调查,将此圆半径设置为2 m.设置仿真初始值:在t0时刻,假设机动车坐标
实验1 设置11个时间步仿真,即i∈[1,11].设置过街行人的位置坐标、速度矢量分别为
| $ \begin{array}{l} \left( {{x_{\rm{O}}}\left( {{t_i}} \right);{y_{\rm{O}}}\left( {{t_i}} \right)} \right) = \left( {6,5,4,3,2,1,0, - 1, - 2,} \right.\\ \left. { - 3, - 4;40,41,42,43,44,45,46,47,48,49,50} \right), \end{array} $ |
| $ \begin{array}{l} \left( {{v_{{\rm{O}}x}}\left( {{t_i}} \right);{v_{{\rm{O}}y}}\left( {{t_i}} \right)} \right) = \left( { - 1, - 1, - 1, - 1, - 1, - 1,} \right.\\ \left. { - 1, - 1, - 1, - 1, - 1;1,1,1,1,1,1,1,1,1,1,1} \right). \end{array} $ |
假设车辆满足跟驰约束,通过仿真实验,得到实验结果如图 5所示.结果显示:由行人的坐标来看,大约在第6个时间步的时候,行人到达交织点,即46 m处.而机动车在6 s时已到达50 m处.机动车采用加速策略进行避让.

|
图 5 车辆直行加速 Fig. 5 Acceleration for straight movement vehicles |
实验2 设置行人位置坐标、速度矢量分别为
| $ \begin{array}{l} \left( {{x_{\rm{O}}}\left( {{t_i}} \right);{y_{\rm{O}}}\left( {{t_i}} \right)} \right) = \left( {6,5,4,3,2,1,0, - 1, - 2,} \right.\\ \left. { - 3, - 4;50,51,52,53,54,55,56,57,58,59,60} \right), \end{array} $ |
| $ \begin{array}{l} \left( {{v_{{\rm{O}}x}}\left( {{t_i}} \right);{v_{{\rm{O}}y}}\left( {{t_i}} \right)} \right) = \left( { - 1, - 1, - 1, - 1, - 1, - 1,} \right.\\ \left. { - 1, - 1, - 1, - 1, - 1;1,1,1,1,1,1,1,1,1,1,1} \right). \end{array} $ |
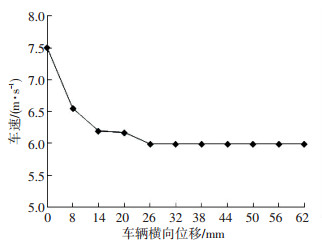
通过仿真实验,得到实验结果如图 6所示.结果显示,由行人的坐标来看,大约在第6个时间步的时候,行人已经到达交织点56 m处,此后行人通过交织点.而机动车在9 s后才到达该点,两者相差3 s.机动车采用减速策略进行避让.
|
图 6 车辆直行减速 Fig. 6 Deceleration for straight movement vehicles |
设置12个时间步仿真,i∈[1,12].设置过街行人的位置坐标、速度矢量分别为
| $ \begin{array}{l} \left( {{x_{\rm{O}}}\left( {{t_i}} \right);{y_{\rm{O}}}\left( {{t_i}} \right)} \right) = \left( {6,5,4,3,2,1,0, - 1, - 2, - 3,} \right.\\ \left. { - 4, - 5;40,41,42,43,44,45,46,47,48,49,50,51} \right), \end{array} $ |
| $ \begin{array}{l} \left( {{v_{{\rm{O}}x}}\left( {{t_i}} \right);{v_{{\rm{O}}y}}\left( {{t_i}} \right)} \right) = \left( { - 1, - 1, - 1, - 1, - 1, - 1,} \right.\\ \left. { - 1, - 1, - 1, - 1, - 1;1,1,1,1,1,1,1,1,1,1,1} \right). \end{array} $ |
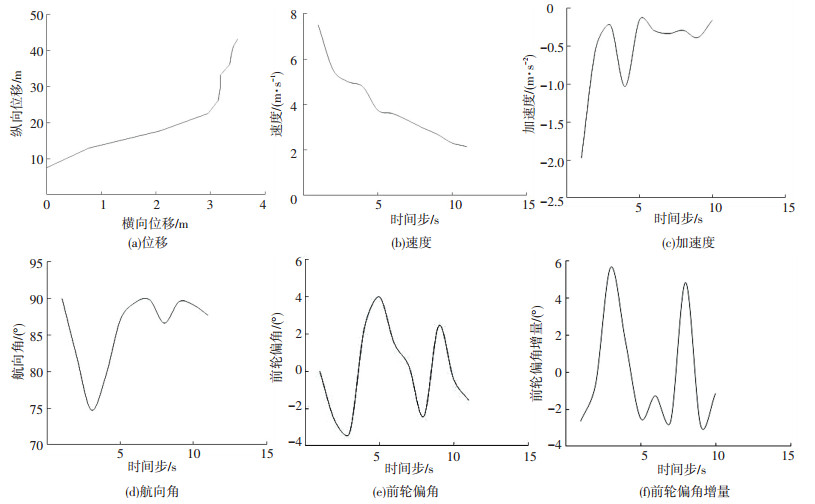
本文假设车辆满足换道约束,通过仿真实验,得到实验结果如图 7所示.结果显示,在满足车辆变化率最小的目标下,车辆的控制策略是先直行9 m,减速后再向右侧换道,控制车辆一共行驶43 m.车辆采用了减速让行策略,即行人通过潜在冲突点后车辆再到达该点.从加速度及速度变化来看,车辆在直行阶段速度快,在转向换道阶段速度变缓,速度标准差为1.102 s.从航向角变化来看,车辆的航向角在转向开始之初变化快,然后逐渐变缓,航向角稳定在90°左右,这些特征都与车辆实际的换道过程相符合,因此实验结果有效.此外,算法求解出的车辆换道时间为10 s,不会引起乘坐人员的不适.
|
图 7 车辆换道策略结果分析 Fig. 7 Analysis of the result of vehicle's lane changing strategies |
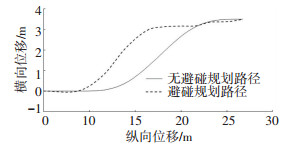
借鉴文献[16]中研究成果,采用七次多项式对无避碰状态下的车辆的换道轨迹进行规划,选择与避碰车辆相同的起终点,得到车辆的规划换道路径,如图 8所示,图中的虚线为计算得到的避碰的车辆规划换道路径,从图中可以看到,两条曲线的变化趋势基本吻合,说明仿真过程中的车辆各种动力学信息与现实中车辆换道过程的状态信息相符合.但是,从轨迹对比明显可以看出,避碰条件下车辆会提前进行换道,以规避风险.此处引入风险感知系数k评价两种情况下的风险感知,其中k与车辆的速度v成反比,与车辆距离障碍点的距离l成正比,即
|
图 8 避碰与无避碰状态下换道轨迹对比 Fig. 8 Comparison of the lane change trajectories under collision avoidance and no collision avoidance |
| $ k = \frac{l}{v}, $ | (32) |
则刚开始换道时两种情形的风险感知系数:1)无避碰规划路径中的风险感知系数k1=(43-13.5)/7.5= 3.933;2)避碰规划路径中的风险感知系数k2=(43-7.5)/5.5=6.455.同理,求出换道过程中其他各点的风险感知系数.则无避碰规划路径中的平均风险感知系数k1 =2.062,避碰规划路径中的平均风险感知系数k2 =3.681.由于k1 < k2,故避碰规划路径安全性更高.
5 结论1) 基于速度障碍理论构建了车辆对行人自主避碰控制的车辆预测模型,对控制方法的基本原理、控制目标、约束条件等进行了分析,并通过仿真方法对控制的实施效果进行验证.仿真结果表明,该控制方法实现了车辆对过街行人的避让,且从结果来看该控制方法合理、有效、可行.这丰富和扩展了智能车安全驾驶辅助技术的研究理论框架和分析方法,为复杂环境下的车辆避碰系统设计提供了依据.
2) 从仿真结果来看,车辆的换道曲线并不平滑,与现实会有细微偏差,这是因为遗传算法在求解最优化结果时存在不稳定的原因,因此研究更为稳定且效果更高的求解算法应用于智能车辆的轨迹规划是非常必要的.
3) 仿真场景的设计目前考虑的是单辆车与单个行人的情况,将仿真场景设计成多辆车与多个行人的情形将是下一步研究的重点.
| [1] |
ROTHMAN L, HOWARD A W, CAMDEN A, et al. Pedestrian crossing location influences injury severity in urban areas[J]. Injury Prevention Journal of the International Society for Child & Adolescent Injury Prevention, 2012, 18(6): 365. |
| [2] |
PFORTMUELLER C A, MARTI M, KUNZ M, et al. Injury severity and mortality of adult zebra crosswalk and non-zebra crosswalk road crossing accidents: a cross-sectional analysis[J]. PloS One, 2014, 9(3): e90835. |
| [3] |
吕能超, 旷权, 程启超, 等. 基于车路协同与机器视觉的行人防碰撞系统[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(4): 702. LV Nengchao, KUANG Quan, CHENG Qichao, et al. Pedestrian-vehicle collision avoidance system based on cooperative vehicle infrastructure system and machine vision[J]. Journal of Wuhan University of Technology (Traffic Science and Engineering Edition), 2015, 39(4): 702. DOI:10.3963/j.issn.2095-3844.2015.04.006 |
| [4] |
ANAYA J J, MERDRIGNAC P, SHAGDAR O, et al. Vehicle to pedestrian communications for protection of vulnerable road users[C]//Intelligent Vehicles Symposium Proceedings. New York: Curran Associates, Inc., 2014: 1037
|
| [5] |
LIU Zhenyu, PU Lin, ZHU Konglin, et al. Design and evaluation of V2X communication system for vehicle and pedestrian safety[J]. The Journal of China Universities of Posts and Telecommunications, 2015, 22(6): 18. |
| [6] |
黄子超, 吴青, 马育林.基于模型预测控制与环境势场建模的车队协同驾驶方法研究[C]//第十一届中国智能交通年会大会论文集.北京: 电子工业出版, 2016: 249 HUANG Zichao, WU Qing, MA Yulin. A study on collaborative platoon driving method based on APF method and MPC control[C]//Proceedings of the 11th China Intelligent Transportation Conference. Beijing: Publishing House of Electronics Industry, 2016: 249 |
| [7] |
徐成.部分车辆联网条件下多车协同避撞算法研究[D].北京: 清华大学, 2015 XU Cheng. Research on the algorithm of coordinated collision avoidance in partial-connected driving environment[D]. Beijing: Tsinghua University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10003-1016712692.htm |
| [8] |
SHV N, SHOVAL S, HACOHEN S. Dynamic model for pedestrian crossing in congested traffic based on probabilistic navigation function[J]. Transportation Research Part C Emerging Technologies, 2017, 86: 78. |
| [9] |
XIAO Yao, GAO Ziyou, QU Yunchao, et al. A pedestrian flow model considering the impact of local density: Voronoi diagram based heuristics approach[J]. Transportation Research Part C Emerging Technologies, 2016, 68: 566. |
| [10] |
FIORINI P. Motion planning in dynamic environments using velocity obstacles[J]. International Journal of Robotics Research, 1998, 17(7): 760. |
| [11] |
杨秀霞, 周硙硙, 张毅. 基于速度障碍圆弧法的UAV自主避障规划研究[J]. 系统工程与电子技术, 2017, 39(1): 168. YANG Xiuxia, ZHOU Weiwei, ZHANG Yi. Automatic obstacle avoidance planning for UAV based on velocity obstacle arc method[J]. System Engineering and Electronic Technology, 2017, 39(1): 168. |
| [12] |
HUANG Yamin, GELDER P, WEN Yuanqiao. Velocity obstacle algorithms for collision prevention at sea[J]. Ocean Engineering, 2018, 151: 308. |
| [13] |
蔡逸飞.基于速度障碍的结伴行人运动模型[D].南京: 南京理工大学, 2017 CAI Yifei. A group pedestrian model based on velocity obstacle theory[D]. Nanjing: Nanjing University of Science & Technology, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10288-1017053097.htm |
| [14] |
ZHONG Xunyu, ZHONG Xungao, PENG Xiafu. Velocity change space based dynamic motion planning for mobile robots navigation[J]. Neurocomputing, 2014, 143(2): 153. |
| [15] |
美国交通研究委员会. 道路通行能力手册[M]. 北京: 人民交通出版社, 2007. Transportation Research Board. Highway capacity manual[M]. Beijing: China Communication Press, 2007. |
| [16] |
王畅, 郭应时, 郑楚清.基于七次多项式的智能车换道轨迹规划与仿真[C]// 2012中国汽车工程学会汽车安全技术学术会议.芜湖: 安徽师范大学出版社, 2012 WANG Chang, GUO Yingshi, ZHENG Chuqing. Lane change trajectory planning and simulation for intelligent vehicle based on 7 polynomials[C]//2012 China Automotive Engineering Society Automotive Safety Technology Conference. Wuhu: Anhui Normal University Press, 2012 |
 2019, Vol. 51
2019, Vol. 51


