短时交通流的预测是交通管理部门采取交通控制和诱导措施的重要依据.通过对短时交通流的预测,可以提前调整交通管理控制手段,提高交通运行效率.为了更好反应道路交通运行状态,交通流的短期实时预测是智能交通领域研究重点.交通流数据是时间序列数据,随着机器学习及深度学习的推进,对交通流的预测方法也在不断改善.
早期交通流的预测是基于传统统计学理论.对于统计模型,如将时间序列模型应用于交通流预测领域[1].采用卡尔曼滤波的对交通量预测,引入线性系统状态方程对整体状态进行最优估计[2].马尔科夫预测模型利用时间序列转移概率预测未来时间序列的状态,但不适用于长期预测[3].
在机器学习预测方法中,文献[4]利用模糊神经网络建立了每个路段及整个路网的交通流预测模型,采用模拟测试数据进行验证;文献[5]采用动态小波神经网络进行实际交通流预测,文献[6]提出采用SVM回归模型的交通状态实时预测.文献[7]提出了基于时间维度、上游路段、下游路段和时空参数4种状态向量的K近邻模型,研究各参数对预测精度的影响.文献[8]提出采用深度信念网络对数据先进行特征学习提取,再采用顶层SVM模型进行预测.文献[9]提出了采用分布式梯度优化决策树筛选特征向量建立DUTP-GBDT模型.
当前深度学习方法广泛应用在时间序列数据预测中.文献[10]通过对循环神经网络精细化调参实现了对城市快速路车速的实时预测.文献[11]采用多网格搜索优化参数选取的LSTM模型对飞机故障事件序列进行预测.文献[12]采用LSTM和ARMA对惯性器件的随机误差进行了误差滤波拟合.
目前对于LSTM参数选取研究多是采用遍历多网格搜索算法、控制变量精细调参,计算开销大.针对高速公路交通流时间序列数据,提出一种GA-LSTM循环神经网络的交通流预测方法.采用遗传算法优化LSTM网络参数,以预测误差最小为目标,采用广深高速公路交通数据展开实验,同其他时间序列预测模型进行对比,结果显示GA-LSTM模型在交通流短时预测中适应性更好,具有良好的预测性能.
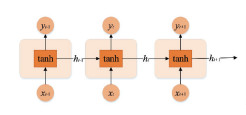
1 长短期记忆模型介绍循环神经网络(recurrent neural network,RNN)是在网络结构中以单元结构连接为有向图的神经网络[13],RNN神经网络可以存储神经元当前时刻的输入与之前时刻的输出关系[14]. RNN神经网络近年也被用在非线性时间序列数据的预测中[15].图 1为简单的RNN的典型链式结构.
|
图 1 RNN典型链式结构 Fig. 1 RNN typical chain structure |
对于给定的输入序列xt(i = 1,2,...,N),隐藏层序列模块ht为
| $ {h_t} = {f_a}\left( {{W_{xh}}{x_t} + {W_{hh}}{h_{t - 1}} + {b_h}} \right). $ | (1) |
其中:Wxh,Whh分别表示从输入x到隐藏状态h、隐藏状态h到自身的连接权值,下标t为时间;bh为偏置矢量;fa为隐藏层的激活函数.
输出序列yt为
| $ {y_t} = {f_b}\left( {{W_{ho}}{h_t} + {b_y}} \right). $ | (2) |
其中:Who表示从隐藏状态到输出y的连接权值,by为偏置矢量,fb为输出层的激活函数.
RNN实现长期记忆计算的功能与前n次计算相关,由于功能有限,RNN的记忆能力很弱,计算量加大导致模型训练时间增加,并产生梯度消失和梯度爆炸问题.基于对RNN神经网络进行改进,通过在链式结构中引入LSTM模块,LSTM具有复杂的动力学结构,可以从输入数据中学习长期计算记忆信息[16].
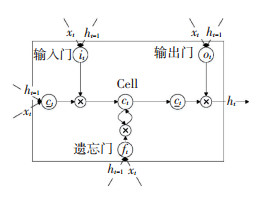
如图 2所示,在LSTM的计算单元中有输入门it、遗忘门ft、输出门ot,单元状态ct、隐藏状态ht,采用激活函数和逐点乘法运算形成门限,使LSTM单元具有计算长距离历史信息的能力.
|
图 2 LSTM计算单元内部结构 Fig. 2 Internal structure of the LSTM calculation unit |
输入门it决定需要更新的单元,表示为
| $ {i_t} = \sigma \left( {{W_{xi}}{x_i} + {W_{hi}}{h_{t - 1}} + {W_{ci}}{c_{t - 1}} + {b_i}} \right). $ | (3) |
其中W和b分别为权值矩阵和偏移量.
遗忘门ft决定需要保留的历史信息,表示为
| $ {f_t} = \sigma \left( {{W_{xf}}{x_t} + {W_{hf}}{h_{t - 1}} + {W_{cf}}{c_{t - 1}} + {b_f}} \right). $ | (4) |
进而对模型的状态进行更新,有
| $ {c_t} = {f_t}{c_{t - 1}} + {i_t}\tanh \left( {{W_{xc}}{x_t} + {W_{hc}}{h_{t - 1}} + {b_c}} \right). $ | (5) |
输出门ot在LSTM单元输出计算结果为
| $ {o_t} = \sigma \left( {{W_{xo}}{x_t} + {W_{ho}}{h_{t - 1}} + {W_{co}}{c_t} + {b_o}} \right). $ | (6) |
其中σ为激活函数.
获得隐藏状态信息为
| $ {h_t} = {o_t}\tanh \left( {{c_t}} \right). $ | (7) |
其中tanh为激活函数.
LSTM的训练时,首先按照前向传播计算LSTM单元的输出值,计算LSTM单元的误差值并反向传播;根据误差值,计算权值梯度;采用优化算法进行梯度下降,实时递归[17]并更新权值.
神经网络优化算法包括随机梯度下降(stochastic gradient descent,SGD)、将梯度积累改变成指数加权移动平均RMSprop算法、自适应学习速率的AdaGrad算法、适应性时刻的Adam算法等. Adam算法在迭代过程中采用平稳梯度代替了原始随机梯度,并引入纠偏机制,使学习速率保持在确定范围,在深度学习中使用较多[18].
大规模神经网络具有耗时长和容易过拟合的缺陷[19].通常采用集成方法训练多个模型进行集成学习,提高模型泛化能力.文献[20]提出dropout方法在模型训练过程中,暂时以概率P随机丢弃隐藏层神经元,则每个批次数据都在训练不同的网络,得出精度较高的预测结果.
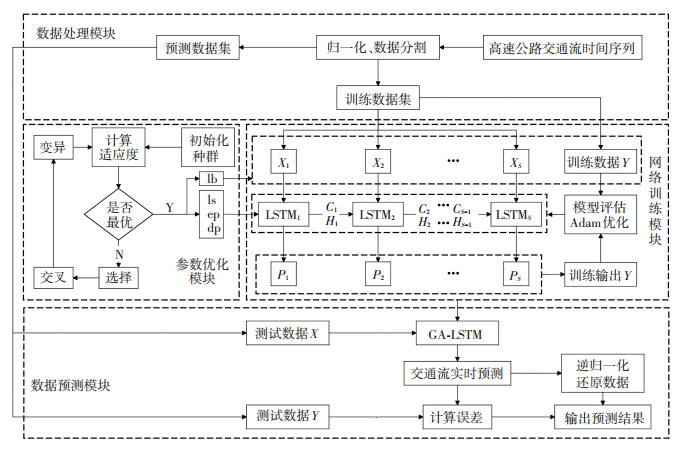
2 基于GA-LSTM的交通流预测模型 2.1 模型预测流程建立GA-LSTM交通流预测模型,整体框架如图 3所示,包括数据处理模块、参数优化模块、网络训练模块、网络预测模块.采用遗传算法对数据时间窗步长(look_back,lb)、LSTM模型中的网络隐藏层(lstm_nets,ls)、训练次数(epochs,ep)、dropout(dp)4个参数在搜索空间优化,确定最佳参数组合.将交通流时间序列作为输入数据,将下一阶段交通流的预测值作为输出矩阵,通过长短期记忆循环神经网络迭代自适应调整模型权重,拟合形成GA-LSTM模型.将测试数据输入进行预测,将预测结果与实际测试数据进行误差对比并输出.
|
图 3 基于GA-LSTM的交通流预测框架 Fig. 3 Traffic flow prediction framework based on GA-LSTM |
交通流数据是非平稳随机序列,本文构建的GA-LSTM模型对数据导入后进行归一化,将特征映射到(0,1)区间里,将交通量转化为有监督学习模式,将上一阶段的数据作为当前阶段数据的输入[21].
在数据处理模块中,读取获得原始交通流时间序列
| $ {d_i} = \frac{{{f_{di}} - \mathop {\min }\limits_{1 \le j \le n} \left\{ {{f_{dj}}} \right\}}}{{\mathop {\max }\limits_{1 \le j \le n} \left\{ {{f_{dj}}} \right\} - \mathop {\min }\limits_{1 \le j \le n} \left\{ {{f_{dj}}} \right\}}}. $ | (8) |
获得新数据序列D={d1,d2,…,dn},分为训练数据集和测试数据集分别为dtr={d1,d2,…,dm}和dte={dm+1,dm+2,…,dn}.
对数据进行时间窗步长处理,设定时间窗步长lb设定为S,则处理后数据输入为
| $ X = \left\{ {{X_1},{X_2}, \cdots ,{X_S}} \right\}. $ | (9) |
| $ {X_i} = \left\{ {{d_i},{d_{i + 1}}, \cdots ,{d_{m - S + p - 1}}} \right\},1 \le i \le S;i,S \in N. $ | (10) |
实际对比数据为
| $ Y = \left\{ {{Y_1},{Y_2}, \cdots ,{Y_S}} \right\}, $ | (11) |
| $ {Y_i} = \left\{ {{d_{i + 1}},{d_{i + 2}}, \cdots ,{d_{m - S + p}}} \right\}. $ | (12) |
遗传算法是基于生物进化理论发展形成的启发式搜索算法,将目标问题转化为生物进化过程,通过交叉、变异、复制等操作产生新的种群,淘汰适应度低的解.现将问题通过二进制编码形成基因和个体,组成种群.通过对种群个体适应度通过轮盘赌算法进行选择,对个体进行交叉、变异,形成新的种群,迭代运算至满足目标问题.
LSTM模型的预测精度同参数取值密切相关,需要对ls、lb、ep、dp在搜索空间内寻优.多网格搜索算法和精细调参的方式,本质都是对搜索空间的遍历寻优.本文采用遗传算法对LSTM涉及到的参数进行调整优化,获取搜索空间的最优解,形成复合GA-LSTM模型.主要流程步骤为:1)种群初始化并解码. 2)将LSTM神经网络的均方误差作为适应度函数. 3)将解的个体进行选择交叉变异操作. 4)若适应度函数目标值达到最优值,则进行下一步;否则返回第3步. 5)步获得适应度目标值和最佳参数. 6)计算基于最佳参数的预测均方误差. 7)终止条件判断.若种群迭代次数满足,则停止计算,此时LSTM网络全局最优参数组合[ls,lb,ep,dp];否则返回第6步.
2.4 网络训练将处理好的测试数据X输入到GA-LSTM隐藏层中,GA-LSTM单元受前一阶段训练模型影响,输出预测数据为
| $ P = \left\{ {{P_1},{P_2}, \cdots ,{P_S}} \right\}, $ | (13) |
| $ {P_p} = {\rm{GA - LST}}{{\rm{M}}_{{\rm{cal}}}}\left\{ {{X_p},{C_{p - 1}},{H_{p - 1}}} \right\}. $ | (14) |
式中Cp-1、Hp-1分别为前一GA-LSTM单元的状态和输出,GA-LSTMcal为循环神经网络的计算过程.网络训练损失函数采用均方误差,即
| $ L = \sum\limits_{i = 1}^{S\left( {m - S} \right)} {{{\left( {{p_i} - {y_i}} \right)}^2}} /[S(m - S)]. $ | (15) |
在GA-LSTM模型中采用经遗传算法选定好的参数,优化目标为损失函数最小化,采用Adam优化算法对网络迭代更新调整模型权重、降低预测误差.
2.5 网络预测采用训练好GA-LSTM模型,对输入预测数据进行预测.
在训练集中实际数据Y的最后一行数,即
| $ {Y_f} = \left\{ {{d_{m - S + 1}},{d_{m - S + 2}}, \cdots ,{d_m}} \right\}. $ | (16) |
采用GA-LSTM模型对Yf进行预测,输出结果为
| $ {P_f} = {\rm{GA - LSTM}}\left( {{Y_f}} \right) = \left\{ {{P_{m - S + 2}},{P_{m - S + 3}}, \cdots ,{P_{m + 1}}} \right\}. $ | (17) |
GA-LSTM网络在m+1时刻预测数值为Pm+1,将Yf的数据剔除第1个,增加Pm+1,组合形成新的数据为
| $ {Y_{f + 1}} = \left\{ {{d_{m - S + 2}},{d_{m - S + 3}}, \cdots ,{P_{m + 1}}} \right\}. $ | (18) |
并将Yf+1输入到GA-LSTM,以此方法得到Pm+2,进行迭代,从而获取预测的时间序列为
| $ {P_{te}} = \left\{ {{P_{m + 1}},{P_{m + 2}}, \cdots ,{P_n}} \right\}. $ | (19) |
将预测结果Pte与真实数据dte进行还原对比,求出模型预测精度.
3 实验评估指标与环境 3.1 实验对比模型支持向量机回归. SVM算法在分类和回归处理中均有应用.在处理回归问题时让所有样本点逼近超平面,求出总偏差最小的超平面[22].本文采用高斯径向基函数(RBF),将交通量映射到高维空间(Hilbert空间)后执行线性回归运算.
最近邻算法回归. KNN采用K个邻近数据来代表样本.通过找出样本的K个欧氏距离邻近数据,将这些数据的属性的平均值赋给该样本,得到该样本的属性[23].将不同距离的邻近数据对该样本产生的影响赋给不同权重[7].结合网格搜索和交叉验证,提高预测精度,实现近似线性可分.
BP神经网络回归.神经网络是由一组相互连接的神经元组成,彼此连接有权重控制.数据结构对特征变量比较适应度灵活,可以设置多个非线性的隐藏层,适合对复杂非线性数据进行预测[24].在回归预测中采用非线性函数输出,采用Adam和反向传播算法进行训练.在训练数据量大的情况下预测效果好.
传统LSTM神经网络回归. LSTM神经网络采用门限结构对循环神经网络进行改造,解决了循环神经网络在较长时间序列回归预测中的梯度消失和梯度爆炸问题.文献[10]在研究车速预测时选用dropout为0.2,文献[19]研究选用时间窗步长、网络隐藏层进行组合研究.综合上述研究,本文选定对比LSTM模型的时间窗步长为3,网络隐藏层数为50,epochs为200,dropout为0.2.
3.2 实验评估指标为了定量分析GA-LSTM模型性能,采用均方误差(EMS)和均方根误差(ERMS)作为评估指标,并与SVM、KNN、BP、LSTM算法进行对比. EMS和ERMS的值越小,代表预测精度越高.均方误差和均方根误差分别为
| $ {E_{{\rm{MS}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{Y_i} - Y_i^*} \right)}^2}} , $ | (20) |
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{Y_i} - Y_i^*} \right)}^2}} } . $ | (21) |
其中:N为数据集个数,Yi为真实数据集,Yi*为预测数据集.
3.3 实现平台实验所使用的计算机配置和软件环境如下:处理器为Intel i5-6500,内存为8.0GB;系统是Windows10(64位);程序语言版本为Python3.6.2;集成开发环境为Anaconda包中的spyder3.28版本. GA-LSTM和BP、LSTM在Keras库中以Tensorflow为后端实现,预测效果对比所用的SVM和KNN模型在scikit-learn库中实现.
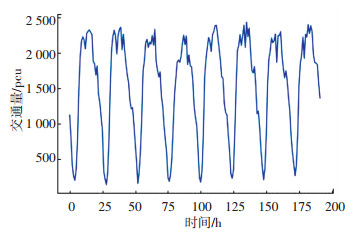
4 实验结果及分析 4.1 交通流数据采集本文选取广州某段高速公路2017年9月20日— 2017年9月27日车道高清卡口检测器的交通流数据作为预测样本.高速公路作为封闭式通行系统,交通流信息真实性高.高速公路管理部门在对车辆进行控制和诱导时,需要提前预估短时间交通流数据,本文数据采集间隔分别为5、15、30、60 min4种.实验以前7天数据为训练样本,第8天数据为测试样本.图 4为以30 min为间隔的8 d交通流数据.高速公路周末同工作日流量相当,数据具有周期性特征.采用前一阶段数据进行下一阶段数据预测.
|
图 4 交通流时间序列 Fig. 4 Traffic flow time series |
采用遗传算法优化LSTM模型参数取值,设置种群中个体为50,迭代次数为100,变异概率pm为0.1,交叉概率pc为0.6,以60 min交通流数据为样本进行分析.
1) 搜索空间. ls为网络层数,10~160,步长为10;采用4位二进制,0000代表 10. lb为时间窗步长,1~16,步长为1;采用4位二进制,0000代表 1. ep为训练次数,10~320,步长为10;采用5位二进制,00000代表 1. dp为dropout,0.2~0.51,步长为0.01;采用5位二进制,00000代表 0.20.
2) 编码.根据参数性质,采用二进制编码,个体中含有18个基因. [0101, 0101, 01010, 01010]表示为某个体,则4段染色体分别表示为参数ls、lb、ep、dp基因型.
4.2.2 遗传算法训练最优值经过训练,结果如图 5所示,在GA-LSTM模型中,可以在搜索空间快速找到近似最优解.随着迭代步数增加,如图 6所示,其最优解的均方误差在减少,实现搜索空间最优解.
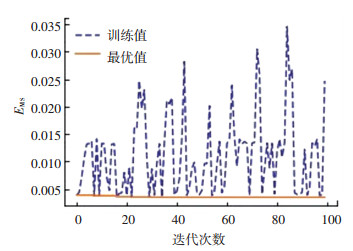
|
图 5 GA-LSTM神经网络训练曲线 Fig. 5 GA-LSTM neural network training curve |
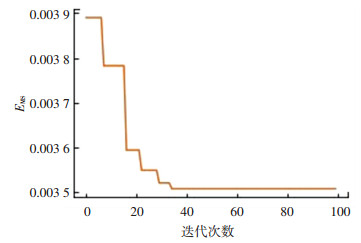
|
图 6 GA-LSTM神经网络收敛曲线 Fig. 6 GA-LSTM neural network convergence curve |
经过100次迭代,对预测误差进行统计描述见表 1.在100次迭代产生的最优值数据中,ls的搜索覆盖范围为10~160;lb的搜索覆盖范围为1~16;ep的搜索覆盖范围为20~320;dp的搜索覆盖范围为0.21~0.52.4种参数的搜索范围接近全搜索空间,所得误差近似最优解.其中最小均方误差为0.003 508,前25%位的均方误差为0.004 328.
| 表 1 100个最优参数组合信息统计描述 Tab. 1 Statistical description of 100 optimal parameter combination information |
对100个最优个体进行统计,如图 7所示,lb,ep与EMS相关性系数分别为-0.68,-0.52,在0.01的水平上显著性相关;ls、dp与EMS的相关系数分别为-0.031、0.037,相关性不大.
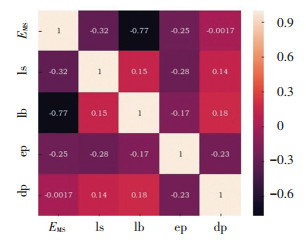
|
图 7 100个最优组合参数相关性 Fig. 7 100 optimal combination parameter correlation |
对25个最优个体统计参数精细对比,如图 8所示,lb和EMS的相关系数为-0.77,具有强相关性;ls、ep分别为-0.23、0.25,具有弱相关性;dp仅为-0.001 7,相关性不大.
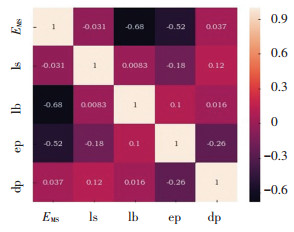
|
图 8 25个最优组合参数相关性 Fig. 8 25 optimal combination parameter correlation |
通过对大规模寻优和精细化调参对比,发现在100次迭代大范围调参过程中,lb、ep对EMS的影响显著性相关,ls、dp对EMS影响不大.在对25最优个体参数精细对比中,lb对EMS具有强相关性,ls、ep对EMS有弱相关性,dp对误差的影响不大.
4.3 预测结果及分析由参数选取分析可得,最佳时间窗步长为13,网络隐藏层数为100,epochs为200,dropout为0.37,随机种子选取7,分别绘制在5种预测模型对4种数据样本的预测结果.
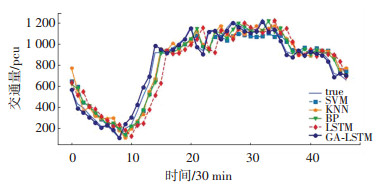
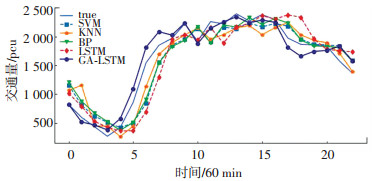
为了清晰对比5种算法预测性能,本文以30 min和60 min的数据进行展示.如图 9、10所示,5种算法均能较好拟合真实数据,相比SVM、KNN、BP、LSTM算法,GA-LSTM在交通流数据突变处表现的更加优越,趋势转变迅速,模型适应性强,预测精度更高.
|
图 9 5种模型30 min数据预测结果 Fig. 9 30 min data forecast results of five models |
|
图 10 5种模型60 min数据预测结果 Fig. 10 60 min data forecast results of five models |
经过5种不同模型的预测4种间隔数据所得EMS和ERMS见表 2.在EMS统计中,次优模型比GA-LSTM模型在4个数据集的预测中分别大6.47%、5.09%、6.16%、29.5%;在ERMS统计中,次优模型比GA-LSTM模型分别大3.18%、7.07%、3.03%、13.8%.
| 表 2 不同模型对4种间隔数据预测结果对比 Tab. 2 Comparison of prediction results of four interval datum by different models |
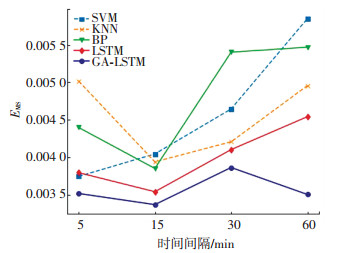
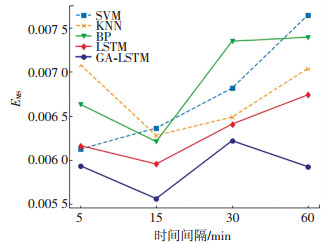
本文所用的GA-LSTM模型同SVM、KNN、BP、LSTM等方法预测精度如图 11、12所示.在5种不同时间间隔数据的预测中,GA-LSTM表现出的均方差和均方根误差均最小. SVM模型在5 min间隔样本中,预测精度和GA-LSTM模型都比较小,随着训练数据量的减少,预测误差在增大,SVM模型更适合交通流短期预测. KNN、BP神经网络、GA-LSTM模型在15 min间隔样本中取得最小误差. GA-LSTM在60 min间隔数据样本预测中优势最大,显示出在数据量较小情况下的优越性. GA-LSTM模型在5种间隔数据中均体现良好的预测性能,显示了模型良好的适用性和扩展性.
|
图 11 5种模型对不同数据预测均方误差对比 Fig. 11 Comparison of mean square error of five models for different data predictions |
|
图 12 5种模型对不同数据预测均方根误差对比 Fig. 12 Comparison of root mean square error of five models for different data predictions |
1) 在介绍LSTM循环神经网络的概念和训练过程基础上,采用遗传算法对时间窗步长、LSTM模型的网络隐藏层、训练次数、dropout四个参数进行取值优化,采用GA-LSTM模型在高速公路交通流预测方面展开研究.
2) 实验结果表明:遗传算法可以快速实现搜索空间参数最优化的取值,寻优效率高;时间窗步长同误差相关性大,训练次数在大范围寻优中影响较大,隐藏层数在精细寻优中有影响,dropout对误差影响小;与常用机器学习算法相比,GA-LSTM在数据预测中的适应性更广、精确度更高,可用于高速公路交通流的预测.
3) 本文虽然是研究短时交通流预测,但该算法也可应用在中长期的交通流预测中.随着深度学习的进一步应用,多源数据的挖掘、考虑多状态交织影响的交通流预测将会成为下一步研究方向.
| [1] |
SMITH B L, DEMETSKY M J. Traffic flow forecasting: comparison of modeling approaches[J]. Journal of Transportation Engineering, 1997, 123(4): 261. |
| [2] |
VYTHOULKAS P C. Alternative approaches to short term traffic forecasting for use in driver information systems[J]. Transportation & Traffic Theory Proceedings of International Symposium on Traffic Flow Theory & Transportation, 1993, 12: 485. |
| [3] |
CHAN K Y, DILLON T S, SINGH J, et al. Neural-network-based models for short-term traffic flow forecasting using a hybrid exponential smoothing and Levenberg-Marquardt algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 644. |
| [4] |
QUEK C, PASQUIER M, LIM B B S. POP-TRAFFIC: a novel fuzzy neural approach to road traffic analysis and prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(2): 133. |
| [5] |
JIANG Y, ADELI H. Dynamic wavelet neural network model for traffic flow forecasting[J]. Journal of Transportation Engineering, 2005, 131(10): 771. DOI:10.1061/(ASCE)0733-947X(2005)131:10(771) |
| [6] |
姚智胜, 邵春福, 高永亮. 基于支持向量回归机的交通状态短时预测方法研究[J]. 北京交通大学学报, 2006, 30(3): 19. YAO Zhisheng, SHAO Chunfu, GAO Yongliang. Research on short-term traffic state prediction based on support vector regression[J]. Journal of Beijing Jiaotong University, 2006, 30(3): 19. DOI:10.3969/j.issn.1673-0291.2006.03.005 |
| [7] |
于滨, 邬珊华, 王明华, 等. K近邻短时交通流预测模型[J]. 交通运输工程学报, 2012, 12(2): 109. YU Bin, WU Shanhua, WANG Minghua, et al. Short-term traffic flow prediction model for K-nearest neighbors[J]. Journal of Transportation and Engineering, 2012, 12(2): 109. |
| [8] |
罗向龙, 焦琴琴, 牛力瑶, 等. 基于深度学习的短时交通流预测[J]. 计算机应用研究, 2017, 34(1): 91. LUO Xianglong, JIAO Qinqin, NIU Liyao, et al. Short-term traffic flow prediction based on deep learning[J]. Journal of Computer Applications, 2017, 34(1): 91. DOI:10.3969/j.issn.1001-3695.2017.01.018 |
| [9] |
黄廷辉, 王玉良, 汪振, 等. 基于Spark的分布式交通流数据预测系统[J]. 计算机应用研究, 2018(2): 405. HUANG Tinghui, WANG Yuliang, WANG Zhen, et al. Spark-based distributed traffic data forecasting system[J]. Research on Application of Computers, 2018(2): 405. DOI:10.3969/j.issn.1001-3695.2018.02.019 |
| [10] |
王祥雪, 许伦辉. 基于深度学习的短时交通流预测研究[J]. 交通运输系统工程与信息, 2018, 18(1): 81. WANG Xiangxue, XU Lunhui. Short-term traffic flow prediction based on deep learning[J]. Journal of Transportation Systems Engineering and, 2018, 18(1): 81. |
| [11] |
王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018, 44(4): 772. WANG Xin, WU Ji, LIU Chao, et al. Exploring LSTM based recurrent neural network for failure time series prediction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(4): 772. |
| [12] |
杨其, 陈水忠, 沈淑梅, 等. LSTM网络和ARMA模型对惯性器件随机误差预测适应性分析[J]. 电光与控制, 2018, 25(3): 68. YANG Qi, CHEN Shuizhong, SHEN Shumei, et al. Adaptive analysis of random error prediction of inertial devices based on LSTM network and ARMA model[J]. Electronics Optics and Control, 2018, 25(3): 68. |
| [13] |
PASCANU R, GULCEHRE C, CHO K, et al. How to construct deep recurrent neural networks[C]// International Conference on Learning Representations. Piscataway, NJ: IEEE Press, 2014: 1235
|
| [14] |
DONG Y, LI D. Automatic Speech Recognition[M]. London: Springer Verlag, 2015: 237.
|
| [15] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(12): 3371. |
| [16] |
MA X, TAO Z, WANG Y, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J]. Transportation Research Part C, 2015, 54: 187. |
| [17] |
HOCHREITER S, SCHMIDHUBER J. Unsupervised coding with lococode[C]// International Conference on Artificial Neural Networks. Berlin, Springer Verlag, 1997: 655
|
| [18] |
KINGMA, DIEDERIK P, BA J. Adam: a method for stochastic optimization[C]//International Conference on Learning Representations.Piscataway, NJ: IEEE Press, 2014: 1572
|
| [19] |
张威威, 李瑞敏, 谢中教. 基于深度学习的城市道路旅行时间预测[J]. 系统仿真学报, 2017, 29(10): 2309. ZHANG Weiwei, LI Ruimin, XIE Zhongjiao. Urban road travel time prediction based on deep learning[J]. System Simulation Journal, 2017, 29(10): 2309. |
| [20] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[J]. Neural and Evolutionary Computing, 2012(7): 1. |
| [21] |
DUNNE S, GHOSH B. Weather adaptive traffic prediction using neurowavelet models[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 370. |
| [22] |
NÓBREGA J P, De Oliveira A L I. Improving the statistical arbitrage strategy in intraday trading by combining extreme learning machine and support vector regression with linear regression models[C]//International Conference on TOOLS with Artificial Intelligence. Piscataway, NJ: IEEE Press, 2014: 182
|
| [23] |
XU Dongwei, WANG Yongdong, JIA Limin, et al. Real-time road traffic states estimation based on kernel-KNN matching of road traffic spatial characteristics[J]. Journal of Central South University, 2016, 23(9): 2453. |
| [24] |
裴玉龙, 王晓宁. 基于BP神经网络的交通影响预测模型[J]. 哈尔滨工业大学学报, 2004, 36(8): 1034. PEI Yulong, WANG Xiaoning. Traffic impact forecast model based on the BP network[J]. Journal of Harbin Institute of Technology, 2004, 36(8): 1034. DOI:10.3321/j.issn:0367-6234.2004.08.012 |
 2019, Vol. 51
2019, Vol. 51


