随着大数据时代的发展,各种手机软件通过采集用户的GPS数据能够广泛收集居民的出行信息,通过这些数据不仅能够有效揭露居民的旅行模式[1-2],了解居民的出行活动[3-5],也能够为城市的交通规划和管理提供重要的参考[6].然而,通过不同交通方式出行的居民其出行模式存在着显著的差异[7],例如:小汽车出行通常会覆盖较大的范围并伴随着较快的速度,但是步行则恰好相反.因此,不同交通出行方式的混淆会对更深一步的挖掘居民的出行模式造成巨大的干扰.
近年来科研学者针对混合多种交通出行模式的GPS数据进行了大量的研究并取得了一定的研究成果.文献[8]利用隐马尔科夫模型对公交车、小汽车、自行车、电动车、火车、地铁、步行、摩托车等8种轨迹进行了识别.文献[9]基于手机的GPS与加速传感器数据,构建了一种多变量参数模型,在对步行和自行车轨迹的识别上能够达到90%以上的精度.文献[10]通过结合地理信息数据,提出了一种GIS算法,实现了对步行、小汽车、公交车、地铁和通勤铁路5种交通方式的轨迹识别.随着人工智能的发展,各种机器学习和深度学习算法也被广泛应用于交通轨迹的分类,文献[11]基于支持向量机(SVM),文献[12]基于神经网络(NN)均能对轨迹实现较好的分类预测.文献[13]对支持向量机、随机森林、K-近邻、决策树等机器学习方法进行了对比.文献[14]使用极端梯度提升模型(XGBoost),并结合全局特征与局部特征对轨迹进行了特征提取,实现了良好的轨迹识别效果.深度学习诸如卷积神经网络(CNN)[15]、循环神经网络(RNN)和深度神经网络(DNN)[16]等均能对GPS轨迹进行有效的交通模式分类和识别.但是现有研究在特征提取时大部分未能考虑地理信息,导致运行状态相似的公交车与小汽车轨迹较易混淆.公交车的运行轨迹与公交线路息息相关,本文基于构建的轻量级梯度提升机(LightGBM)模型,引入Fréchet距离,结合公交线路与公交站点信息进行特征提取,在提高整体轨迹识别效果的同时,也能够有效改善公交轨迹与小汽车轨迹的识别精度.
1 数据描述与处理 1.1 数据描述本文研究所涉及的数据包括被标签(交通模式已知)的GPS轨迹数据和北京市公交网与公交站点数据. GPS数据为在2007年到2012年收集到的182位志愿者的GPS轨迹数据,其中73位志愿者的数据被标签记录,包括步行、自行车、公交车、小汽车、地铁等多种交通出行方式.一条轨迹由多个GPS记录点组成,形式为{r1, r2, r3, …, rn},其中ri表示每一个GPS记录点,每一个GPS记录点记录用户其所处位置的经度、纬度、海拔高度以及时间等信息,其记录格式见表 1,其中91.5%的数据记录为每1~5 s或每5~10 m一个GPS记录点.数据获取自微软亚洲研究院官网的开源资源[17-19].北京市公交网与公交站点数据获取自2013年,包括1 543条公交线路与42 161个公交站点,公交线路由线路上的节点连接而成,形式为{b1, b2, b3, …, bm},公交线路节点与公交站点以经度坐标和纬度坐标的形式记录其地理位置,北京市公交线路和站点分布如图 1所示[20].
| 表 1 GPS记录点的数据格式 Tab. 1 Data format of GPS record point |
|
图 1 北京市公交线网与公交站点分布 Fig. 1 Distribution of bus lines and stations in Beijing |
本文研究范围为北京市(东经115.4°~117.6°,北纬39.4°~41.1°),为了减小随机误差,首先对小于10个GPS轨迹点的轨迹进行剔除,通过筛选,共获得北京市范围内7类共6 744条被标签的轨迹(分别为步行2 007条,自行车1 366条,公交车1 652条,小汽车1 118条,地铁563条,跑步2条,火车36条),平均每条轨迹包含495个GPS记录点.可知跑步以及火车出行的数据量较少,故本研究只针对步行、自行车、公交车、小汽车和地铁5类出行轨迹,共6 707条.
1.2 特征提取 1.2.1 基本信息对于每条被标签的GPS轨迹,需要提取轨迹的属性特征进行模型训练,本文研究所涉及的基本特征包括速度、加速度、转角转变量、停留率、速度转变率、转角转变率等,分别定义如下.
速度是各种交通方式最基本的行驶特征,也是区分不同交通模式的最关键指标,一条轨迹中每两个连续GPS记录点可计算一次瞬时速度,各类轨迹不同的分位速度具有不同的特征,本文对一条轨迹从5分位速度至95分位速度之间的每5分位速度值进行提取,共获得一条轨迹的19个速度特征.速度vi的计算公式为
| $ {v_i} = \frac{d}{t}. $ |
式中:vi为用户在轨迹记录点ri处的瞬时速度,d为ri与ri+1间的实际地理距离,t为ri与ri+1间的间隔时间.
加速度是一项重要的行驶特征,每两个连续瞬时速度可以进行一次加速度的计算,同样对轨迹的每5分位加速度进行提取,共获得一条轨迹的19个加速度特征.加速度ai的计算公式为
| $ {a_i} = \frac{{{v_{i + 1}} - {v_i}}}{t}. $ |
式中ai为用户在轨迹记录点ri处的瞬时加速度.
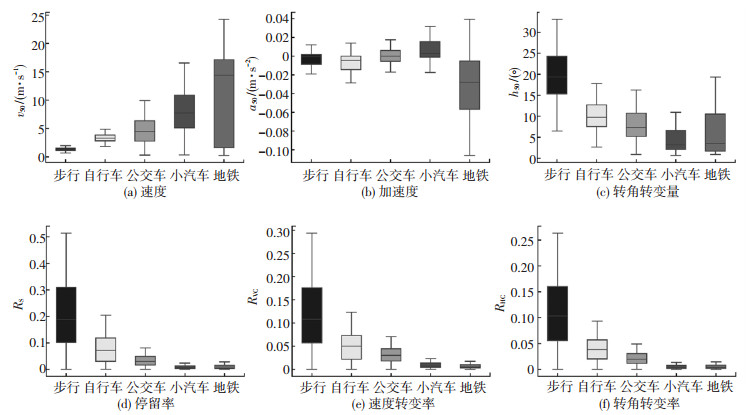
转角转变量也是轨迹的一项重要特征,如图 2(c)所示,公交车、小汽车和地铁的转角转变量较小,而步行的转角转变量则较大.每相邻两个GPS记录点可以计算一次转角转变量,同样对轨迹的每5分位转角转变量进行提取,共获得一条轨迹的19个转角转变量特征.转角转变量hi的计算公式为
|
图 2 轨迹基本特征分布 Fig. 2 Basic features distribution |
| $ {h_i} = \left| {{H_{i + 1}} - {H_i}} \right|. $ |
式中Hi为用户在轨迹记录点ri处的行驶方向与正北方向的夹角.
停留率是一条轨迹在单位距离内轨迹点瞬时速度小于某个特定阈值的轨迹点数量,其分布如图 2(d)所示,小汽车和地铁的停留率较小,步行的停留率较大.停留率RS的计算公式为
| $ R_{\mathrm{s}}=\frac{\left|P_{\mathrm{s}}\right|}{D} $ |
式中:|Ps|为轨迹中速度小于某个特定阈值的轨迹点的数量,阈值取为3.4 m/s[18],D为轨迹的路径长度.
速度转变率是一条轨迹在单位距离内速率变化大于某个特定阈值的轨迹点数量,其分布如图 2(e)所示,小汽车和地铁的速度转变率较小,步行的速度转变率较大.速度转变率RVC的计算公式为
| $ {R_{{\rm{VC}}}} = \frac{{\left| {{P_v}} \right|}}{D}. $ |
式中:|Pv|为轨迹中速率变化大于某个特定阈值的轨迹点的数量,阈值取为0.26 m/s2[18],速率变化的公式为
| $ {p_i} = \frac{{\left| {{v_i} - {v_{i + 1}}} \right|}}{{{v_i}}}. $ |
转角转变率是一条轨迹在单位距离内转角转变量大于某个特定阈值的轨迹点数量,其分布如图 2(f)所示,同样小汽车和地铁的转角转变率较小,步行的转角转变率较大.转角转变率RHC的计算公式为
| $ {R_{{\rm{HC}}}} = \frac{{\left| {{P_{\rm{c}}}} \right|}}{D}. $ |
式中|Pc|为轨迹中转角转变量大于某个特定阈值的轨迹点的数量,阈值取为19°[18].
其中50分位速度、50分位加速度、50分位转角转变量、停留率、速度转变率与转角转变率的轨迹特征分布如图 2(a)~2(f)所示.
1.2.2 公交地理信息为了对公交轨迹实现更好的识别,融入公交线路与公交站点信息以获得与公交地理信息相关的特征,本文共获得3个公交地理特征,轨迹起点距公交站点距离、轨迹终点距公交站点距离和轨迹同公交线路的Fréchet距离,分别定义如下.
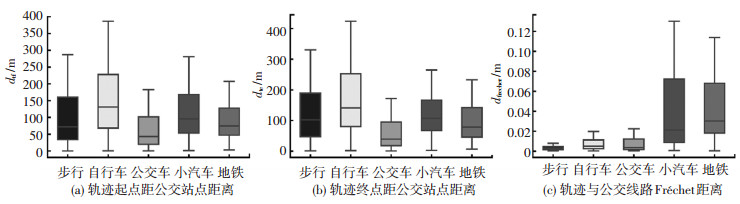
轨迹起点距公交站点距离dtf:轨迹的第一个GPS记录点与最近公交站点的地理距离,其分布如图 3(a)所示,可以看出公交轨迹的距离相对较小.
|
图 3 轨迹地理特征分布 Fig. 3 Geographic features distribution |
轨迹终点距公交站点距离dte:轨迹的最后一个GPS记录点与最近公交站点的地理距离,其分布如图 3(b)所示,同样公交轨迹的距离相对较小.
轨迹与公交线路的Fréchet距离dFréchet(P, Q):Fréchet距离是一种空间路径相似性描述的方法,其重点考虑曲线间的空间距离,对有着空间时序的曲线通过Fréchet距离能够很好地描述曲线间的空间相似程度[21].对于两条由离散的点连接而成的曲线P{r1, r2, r3, …, rn}和Q{b1, b2, b3, …, bm},Fréchet距离的计算方式为
| $ {d_{{\rm{Frécher }}}}(P,Q) = \inf \mathop {\max }\limits_{i \in [1,n],j \in [1,m]} \left\{ {d\left( {{r_i},{b_j}} \right)} \right\}. $ |
式中:P为用户轨迹,Q为公交线路,ri∈{r1, r2, r3, …, rn},bj∈ {b1, b2, b3, …, bm},bj为公交线路的节点集合,d(ri, bj)为两GPS点的距离度量函数.
对于Fréchet距离的计算通过如下步骤:1)对轨迹与公交线路进行匹配,分别筛选距轨迹起点与终点1 500 m之内(图 4中圆形区域)的公交线路集合Bf与Be,获取Bf与Be中共有的公交线路Bf∩Be作为候选公交线(图 4中的公交线路a,b,c). 2)对于每条候选公交线,截取距轨迹起点最近的公交线节点和距轨迹终点最近的公交线节点的公交线范围作为候选截断公交线. 3)分别计算轨迹与候选截断公交线的Fréchet距离,选定Fréchet距离最小值作为该轨迹的Fréchet距离特征(图 4中的公交线路a为Fréchet距离最小值所对应的公交线).

|
图 4 轨迹与公交线路Fréchet距离计算示意 Fig. 4 Calculation of Fréchet distance between trajectory and bus line |
不同轨迹的Fréchet距离分布如图 3(c)所示,可以看出步行、自行车与公交车轨迹的Fréchet距离明显较小,而小汽车与地铁轨迹的Fréchet距离则相对较大.
2 GPS轨迹交通模式识别模型 2.1 模型介绍轻量级梯度提升机(LightGBM)基于梯度提升决策树(GBDT),是一种基于直方图(Histogram)的决策树算法,其通过加法模型和前向分步算法实现学习的优化,较比传统的GBDT,LightGBM通过直方图方式对连续特征值进行分段,能够实现更快的模型训练速度并节省内存,并且通过leaf-wise的生长策略对树进行生长,并限制树的深度以防止过拟合,能够有效提高模型预测的准确率. LightGBM是微软开发的一种开源分类预测算法,本研究通过调用python的lightgbm模块实现. LightGBM的具体实现流程如下.
模型训练阶段:
输入:训练数据Xtrain, Ytrain
1、确定目标函数:
| $ {\rm{ob}}{{\rm{j}}^t} = \sum\limits_{i = 1}^n l \cdot \left( {{y_i},y_i^{(t)}} \right) + \sum\limits_{i = 1}^t \mathit{\Omega } f(i) $ |
2、初始化常数:
3、While未达到迭代次数或预设的终止条件:
{
4、计算目标函数,确定梯度下降方向与步长,更新决策树f(t)
4.1、对特征值构建直方图,计算各个切分点的增益,寻找最优分割点
4.2、带有深度限制的Leaf_wise树生长策略,限制树的深度与叶节点的最小样本数
5、更新训练结果:
| $ \hat y_i^{(t)} = \sum\limits_{k = 1}^t {{f_k}} \left( {{x_i}} \right) = \hat y_i^{(t - 1)} + {f_t}\left( {{x_i}} \right) $ |
}
模型测试阶段:
输入:测试数据Xtest
6、加权所有决策树的结果:
输出:测试结果Ytest
其中:xi为某个训练样本或测试样本的特征值,yi为训练样本或测试样本的目标值,n为训练样本的个数,
首先对轨迹特征进行标准化处理,将所有特征值缩放到[0, 1]之间,以避免各特征值量级的不同而导致的误差,公式为
| $ {X_{{\rm{std }}}} = \frac{{{X_i} - {X_{{\rm{min }}}}}}{{{X_{{\rm{max }}}} - {X_{{\rm{min }}}}}} $ |
式中:X为所有轨迹的某一特征值集合,Xi为轨迹i的原特征值,Xstd为轨迹i在进行特性标准化处理后的特征值.
然后通过决策树模型计算轨迹特征(每条轨迹63个特征)与轨迹标签(交通模式)的相关程度,并对每个特征的重要性进行排序(相关程度从大到小排序),筛选重要性排名前n的特征作为模型的输入,用于模型训练与预测.对于模型学习阶段的随机误差,采用5折交叉验证的方式分别构建训练集与测试集并重复运算100遍以保证模型学习的稳定性.
对预测结果精确程度的度量,考虑4个指标,准确率(ACC),精确率(P),召回率(R),与调和平均值(F1),其中准确率为正确分类样本所占的比例,精确率为预测结果为正样本中正确分类样本所占的比例(即查准率),召回率为实际为正样本中被正确分类样本所占的比例(即查全率),调和平均值为综合考虑对精确率与召回率的衡量.计算方式分别为
| $ {A_{{\rm{CC}}}} = \frac{{{T_{\rm{P}}} + {T_{\rm{N}}}}}{{{T_{\rm{P}}} + {T_{\rm{N}}} + {F_{\rm{P}}} + {F_{\rm{N}}}}}, $ |
| $ P = \frac{{{T_{\rm{P}}}}}{{{T_{\rm{P}}} + {F_{\rm{P}}}}}, $ |
| $ R = \frac{{{T_{\rm{P}}}}}{{{T_{\rm{P}}} + {F_{\rm{N}}}}}, $ |
| $ F1 = \frac{{2{T_{\rm{P}}}}}{{2{T_{\rm{P}}} + {F_{\rm{P}}} + {F_{\rm{N}}}}} $ |
式中:TP为将正类预测为正类的样本数量,FN为将正类预测为负类的样本数量,FP为将负类预测为正类的样本数量,TN为将负类预测为负类的样本数量.
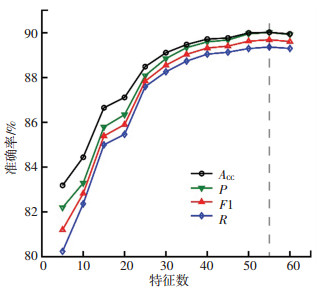
对经由决策树模型筛选的不同特征数量对其预测准确率进行统计,发现当选择特征数量为55个时,预测效果达到较好,如图 5所示,故最终选定模型的特征数n=55.
|
图 5 特征数量与预测精度的关系分布 Fig. 5 Relationship between characteristic quantity and prediction accuracy |
对于未考虑地理特征(dtf、dte与dFréchet(P, Q)),所得预测结果见表 2.
| 表 2 未考虑地理特征的预测结果统计 Tab. 2 Prediction results without reference to geographical features |
由表 2可知步行与自行车出行两种轨迹较易区分,预测精度(精确率和召回率)可达90%以上,但是公交车和小汽车两种交通轨迹较易混淆,预测精度相对稍低.公交车一般沿着公交线路行驶,加入能够突出公交轨迹的公交地理特征后,所得预测结果见表 3.
| 表 3 考虑地理特征的预测结果统计 Tab. 3 Prediction results with reference to geographical features |
可以看出,公交轨迹与小汽车出行轨迹的预测精度得到了有效的提高,公交车轨迹的精确率提高了2%左右,而小汽车轨迹的召回率提高了2.5%左右,表明公交地理特征对这两种轨迹的识别具有重要的作用.两类轨迹在加入公交地理特征前后的精度对比如图 6所示.

|
图 6 公交地理特征加入前后精度对比 Fig. 6 Comparison of prediction accuracy with and without reference to geographical features |
将LightGBM模型与其他机器学习模型:逻辑回归(LR)、K-近邻(KNN)、支持向量机(SVM)、随机森林(RF)、梯度提升决策树(GBDT)、多层感知神经网络(MLP)的预测效果进行对比,各种模型的特征选择与训练方式均保持一致,采用5折交叉验证,重复100次后取平均结果见表 4.
| 表 4 不同模型结果对比 Tab. 4 Prediction results of different models |
可以看出,较比其他机器学习模型,LightGBM模型能够实现更为有效的预测,其预测精度可达90%左右,其他模型如GBDT模型和RF模型相对次之,之后是KNN模型和MLP模型,LR模型和SVM模型则预测精度相对较差.
3 结论1) 基于被交通模式标记的GPS轨迹,利用轻量级梯度提升机(LightGBM)分类模型对交通出行轨迹进行了识别,考虑速度、加速度、转角等多种因素,并结合公交地理信息,引入Fréchet距离对GPS轨迹进行特征提取,实现了对GPS轨迹的交通模式分类.
2) 加入公交地理信息能够对公交轨迹与小汽车轨迹实现更有效地识别,公交轨迹和小汽车轨迹的预测精度均能提高2%左右.
3) 同等条件下较比其他机器学习分类模型,LightGBM能够实现更为有效的轨迹分类预测,整体预测精度达到90%(整体预测精度即综合考虑准确率、精确率、召回率与调和平均值4种指标的预测精度,其中准确率为90.02%,精确率为90.01%,召回率为89.36%,调和平均值为89.69%),其中步行和自行车出行两类轨迹预测精度可达90%以上.
4) 本研究能够对由手机软件收集的用户GPS轨迹实现有效的交通模式分类,从而更为有效地了解用户的出行行为与出行特性,能够为城市交通的规划及商业布局提供良好的基础信息.与公交轨迹相似,地铁轨迹是沿着地铁线运行,将来可结合地铁线路信息进行更深入的特征提取以对该轨迹分类方法实现进一步的优化.
| [1] |
SADEGHVAZIRI E, ROJAS M B, JIN X. Exploring the potential of mobile phone data in travel pattern analysis[J]. Transportation research record, 2016, 2594(1): 27. DOI:10.3141/2594-04 |
| [2] |
王璞, 黄智仁, 龚航. 大数据时代的交通工程[J]. 电子科技大学学报, 2013, 42(6): 806. WANG Pu, HUANG Zhiren, GONG Hang. Transportationengineering in the big data era[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(6): 806. DOI:10.3969/j.issn.1001-0548.2013.06.002 |
| [3] |
WANG P, HUNTER T, BAYEN A M, et al. Understanding road usage patterns in urban areas[J]. Scientific Reports, 2012, 2: 1001. DOI:10.1038/srep01001 |
| [4] |
HUANG Z, WANG P, ZHANG F, et al. A mobility network approach to identify and anticipate large crowd gatherings[J]. Transportation Research Part B: Methodological, 2018, 114: 147. DOI:10.1016/j.trb.2018.05.016 |
| [5] |
ZHENG Z, HUANG Z, ZHANG F, et al. Understanding coupling dynamics of public transportation networks[J]. EPJ Data Science, 2018, 7(1): 23. |
| [6] |
HE K, XU Z, WANG P, et al. Congestion avoidance routing based on large-scale social signals[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 17(9): 2613. |
| [7] |
胡晓伟, 王健, 孙广林. 有限理性下出行者方式选择行为[J]. 哈尔滨工业大学学报, 2011, 43(12): 114. HU Xiaowei, WANG Jian, SUN Guanglin. Traveler's mode choice behavior analysis under bounded rational[J]. Journal of Harbin Institute of Technology, 2011, 43(12): 114. |
| [8] |
WIDHALM P, NITSCHE P, BRANDIE N. Transport mode detection with realistic smartphone sensor data[C]//International Conference on Pattern Recognition IEEE. Tsukuba: IEEE Press, 2012
|
| [9] |
NITSCHE P, WIDHALM P, BREUSS S, et al. A strategy on how to utilize smartphones for automatically reconstructing trips in travel surveys[J]. Procedia-Social and Behavioral Sciences, 2012, 48: 1033. DOI:10.1016/j.sbspro.2012.06.1080 |
| [10] |
GONG H, CHEN C, BIALOSTOZKY E, et al. A GPS/GIS method for travel mode detection in New York City[J]. Computers, Environment and Urban Systems, 2012, 36(2): 131. |
| [11] |
BOLBOL A, CHENG T, TSAPAKIS I, et al. Inferring hybrid transportation modes from sparse GPS data using a moving window SVM classification[J]. Computers, Environment and Urban Systems, 2012, 36(6): 526. DOI:10.1016/j.compenvurbsys.2012.06.001 |
| [12] |
GONZALEZ P A, WEINSTEIN J S, BARBEAU S J, et al. Automating mode detection for travel behaviour analysis by using global positioning systems-enabled mobile phones and neural networks[J]. IET Intelligent Transport Systems, 2010, 4(1): 37. DOI:10.1049/iet-its.2009.0029 |
| [13] |
JAHANGIRI A, RAKHA H A. Applying machine learning techniques to transportation mode recognition using mobile phone sensor data[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2406. |
| [14] |
XIAO Z, WANG Y, FU K, et al. Identifying different transportation modes from trajectory data using tree-based ensemble classifiers[J]. ISPRS International Journal of Geo-Information, 2017, 6(2): 57. DOI:10.3390/ijgi6020057 |
| [15] |
DABIRI S, HEASLIP K. Inferring transportation modes from GPS trajectories using a convolutional neural network[J]. Transportation Research Part C: Emerging Technologies, 2018, 86: 360. |
| [16] |
ENDO Y, TODA H, NISHIDA K, et al. Classifying spatial trajectories using representation learning[J]. International Journal of Data Science and Analytics, 2016, 2(3/4): 107. |
| [17] |
ZHENG Y, ZHANG L, XIE X, et al. Mining interesting locations and travel sequences from GPS trajectories[C]//Proceedings of the 18th International Conference on World Wide Web. Madrid: ACM Press, 2009: 791
|
| [18] |
ZHENG Y, LI Q, CHEN Y, et al. Understanding mobility based on GPS data[C]//Proceedings of the 10th International Conference on Ubiquitous Computing. New York: ACM Press, 2008: 312
|
| [19] |
ZHENG Y, XIE X, MA W Y. Geolife: a collaborative social networking service among user, location and trajectory[J]. IEEE Data Eng Bull, 2010, 33(2): 32. |
| [20] |
LONG Y, THILL J C. Combining smart card data and household travel survey to analyze jobs-housing relationships in Beijing[J]. Computers, Environment and Urban Systems, 2015, 53: 19. |
| [21] |
FRECHET M M. Sur quelques points du calcul fonctionnel[J]. Rendiconti del Circolo Matematico di Palermo (1884-1940), 1906, 22(1): 1. |
 2019, Vol. 51
2019, Vol. 51


