交通拥堵在大城市已发展成为常发性拥堵.为治理拥堵，基于静态交通流分配理论，研究满足交通出行需求的路网供给方案^[1]；基于动态交通流分配理论，研究时变交通需求的实时管理与控制方案^[2]；基于交通拥堵收费理论，研究拥堵收费政策对交通出行需求的影响^[3]等.然而，在处理拥堵问题时，由于这些预测模型的输入变量与假设条件繁多等因素，使得其在实际应用中变得十分复杂.考虑到预测类模型的缺点，提出基于实时监测的宏观基本图理论(macroscopic fundamental diagram, MFD)，用于分析路网的性能，并通过控制策略提高其运行效率；在MFD曲线中存在未饱和(under-saturated)、饱和(saturated)、超饱和(over-saturated)3种状态，分别对应路网中畅通、半拥堵与拥堵3种交通状态^[4]；在区域交通实验与仿真中，拥堵交通流布局不均匀性可影响MFD的散点形状及其存在性^[5-6].形成界限清晰MFD曲线的充分条件是道路网络中所有路段处于单一状态(畅通或拥堵状态)^[7]；在考虑路径选择的条件下，分别基于动态交通流与静态交通分配所形成的MFD曲线具有相同形状^[8].而且，静态交通流分配假设路段车流为稳定交通流，车辆呈均匀分布，路段具有相同流入与流出量，满足形成界限清晰MFD曲线的充分条件，因此，可基于静态交通流分配来获取完整且界限清晰的MFD曲线，用于道路网络性能分析.

传统静态交通流分配(本文指无路段容量约束确定性交通分配)，采用随流量单调递增的路阻函数，主要刻画畅通状态下出行者路径选择与流量分配特征，可称之为静态畅通交通流分配模型.为提高路段阻抗函数的精确性，构建包含速度与交通密度的路阻函数^[9]与不受路段通行能力限制的路阻函数^[10]等.同时，从路段流量与通行能力关系的角度，认为路段流量始终低于通行能力，超过部分将在路段上产生拥堵排队现象^[11]；或者假设当流量接近路段容量或路段最大承受能力时阻抗变化将会十分显著^[12].理论上，拥堵路段的阻抗函数随流量的增加呈单调递减的特征，与传统畅通路段单调递增路阻函数截然不同.因此，利用传统静态畅通交通流分配，仅能获取未饱和状态部分的MFD曲线.如果要基于静态交通流分配，评价拥堵状态交通流分配特点与网络供给特征，并获取超饱和状态MFD曲线，则需要构建静态拥堵交通流分配模型.

关于静态拥堵交通流分配研究相对较少，文献[13-14]提出了基于贝叶斯模型的随机用户均衡模型；文献[15-16]基于静态观点，构建单调递减函数描述拥堵路段阻抗特性，提出了“疏解率”的概念与拥堵非平衡分配方法描述拥堵网络流量，并尝试用于路网服务水平评价.国外学者从静态角度出发，基于排队理论研究拥堵状态下的流量分配问题，提出了近似动态交通流分配方法^[17-19].本文基于随交通流单调递减的拥堵路阻函数，分析拥堵状态下道路用户路径选择特征，给出拥堵状态下的用户均衡与系统最优原理；构建用户均衡与系统最优的静态拥堵交通流均衡分配模型，并证明拥堵用户均衡模型与拥堵用户均衡原理的等价性、模型解的唯一性；给出求解静态拥堵用户均衡模型求解算法；通过算例与传统静态畅通交通分配进行对比分析.

1 拥堵路段阻抗函数

路段交通流有畅通和拥堵两种.畅通定义为路段密度小于临界密度的状态；拥堵定义为路段密度大于临界密度的状态.路段畅通时，由于车流速度随密度的增加而减少、流量随密度的增加而增加，路段通过时间则表现为随着流量单调递增现象.因此，畅通路阻函数呈现单调递增的特征.然而，路段拥堵时，当路段密度继续增大，时间阻抗继续增大，但流量逐渐减少.因此，时间阻抗呈现为随流量单调递减的现象，这与畅通路段阻抗函数单调递增的特点截然相反.因此，要实现拥堵状态下的静态交通分配，需要引入拥堵路段阻抗函数.本文中，阻抗只考虑时间因素.

函数需具备连续、单调递减、允许“阻塞零流”情况、流量允许部分“超载”等特性；同时，还必须体现拥堵路段上的车辆数随着疏解流量的增加而逐渐减少的拥堵疏解现象(拥堵状态下，路段的实际通过流量定义为疏解流量，实际通过时间定义为疏解时间).参考BPR阻抗函数，建立拥堵路段阻抗函数^[15]为

$ {t_a}\left( {{x_a}} \right) = {t_{m,a}}{\left( {1 + \alpha {x_a}/{c_a}} \right)^\beta }. $

(1)

其中t_{m, a}为“阻塞零流”路段的行驶时间，定义为阻塞疏解时间，为了理论计算与实际应用方便，可将车辆在路段拥堵时的最大通过时间作为阻塞疏解时间，本文t_{m, a}取一个足够大的有限值；x_a为路段拥堵状态下的分配流量，即疏解流量；c_a为路段a通行能力；α、β为性能参数，且α>0，β < 0，β < 0可以满足函数的单调递减特性.

在传统畅通路段阻抗函数中，当畅通路段流量为零时，即“畅通零流”路段，说明该路段未被使用，对应的阻抗是路段的自由流状态通过时间；此时，从需求角度判断路段的交通状态，当x_a < c_a时，说明路段需求流量低于路段通行能力，路段为畅通状态，当x_a>c_a时，说明路段需求流量高于路段通行能力，路段为拥堵状态.而在拥堵路段阻抗函数中，当路段疏解流量趋于零时，定义为“阻塞零流”路段，说明该路段已被使用而且拥堵程度非常严重；此时，从供给角度判断路段的交通状态，当x_a < c_a时，说明路段疏解流量低于路段通行能力，路段为拥堵状态，当x_a>c_a时，说明路段疏解的流量高于路段通行能力，路段为畅通状态.

静态拥堵分配中，假设路段车流密度处处均匀，路段具有相同的流入与流出量，车流速度一致.因此，拥堵路段上的车辆数N_a的公式计算为

$ {N_a}\left( {{x_a}} \right) = {t_a}\left( {{x_a}} \right) \cdot {x_a}. $

(2)

式中，由于拥堵路段阻抗函数引入了“阻塞零流”，使得在x_a=0时，N_a(x_a)=0，与实际观察到最大车辆数N_max不相符.这主要因为，理论上，当x_a=0时，t_{m, a}=+∞，而且，$\lim\limits_{x_{a} \rightarrow 0} N_{a}\left(x_{a}\right)=x_{a} \cdot t_{m, a}=N_{\max }$.而在实际中，由于道路网的开放性，路段流量几乎不为零.因此，为了实际应用与理论研究方便，定义x_a≤δ时，路段处于“阻塞零流”状态，δ为足够小的数值.同时，为了确保拥堵车辆数随流量单调递减的过程，各项系数取值时要满足：

$ \left\{ {\begin{array}{*{20}{c}} {{N_{\max }} = {x_a} \cdot {t_{m,a}},\;\;\;{x_a} = \delta ;}\\ {\frac{{{\rm{d}}{N_a}\left( {{x_a}} \right)}}{{{\rm{d}}{x_a}}} = \left[ {{t_a}\left( {{x_a}} \right) + {x_a} \cdot \frac{{{\rm{d}}{t_a}\left( {{x_a}} \right)}}{{{\rm{d}}{x_a}}}} \right] < 0,\quad {x_a} \ge \delta .} \end{array}} \right. $

(3)

2 拥堵交通流分配均衡原理

传统静态畅通交通分配的流量为道路用户的需求流量(畅通条件下，需求流量可以完全加载至路网上，需求以流量的形式体现)，刻画在路网所有路段均畅通的条件下，路段随着承载的车辆增加，需求流量逐渐增加、阻抗增大的特性，并采用单调递增的路阻函数描述该特性.

本文提出的静态拥堵交通流分配，其分配流量为拥堵状态下路网的实际通过流量，即疏解流量(拥堵条件下，需求不能被完全分配至路网，需求以车辆数或密度的形式体现)，刻画在路网所有路段均拥堵的条件下，随着路段所承载车辆数(或密度)的减少，疏解流量逐步增加、阻抗减小的特性，并构造单调递减路阻函数描述该特性.此时，所有路段均满足拥堵状态下的交通特性，从而所有路径均为被使用路径.根据其流量的大小分为非“阻塞零流”路径和“阻塞零流”路径. “阻塞零流”路径表明这类路径处于阻塞状态，其疏解时间为该路径所包含路段的最大行驶时间之和.

2.1 拥堵用户均衡原理

在用户均衡原理中，假设道路用户在完全信息情况下尽量选择可用的最短路径.在静态畅通交通流分配时，新增用户对某条最短路径的选择，将会导致该路径密度、需求流量与出行时间的增加.从而在路网均衡时，同一OD对间所有被使用路径的出行时间相等且最小的，未被使用的路径的出行时间小于或等于最小出行时间，最终大量需求流量选择较短路径上，从而流量集中在较短路径上，较长路径流量较少，甚至未被使用.

在静态拥堵交通流分配时，全部路径均处于拥堵状态，新增用户选择最短路行为，将导致该最短路径车辆数增加与疏解流量的减少(密度增大的添堵行为).道路用户大部分会选择并集中于最短路径，导致最短路径密度增大、速度减小、流量减少、时间增加；而相对较少的用户选择较长路径，较长路径的拥堵情况得到“缓和”，密度减小、速度增大、流量增加、时间减少，直至同一OD间所有路径疏解时间趋于相等，网络达到拥堵用户均衡状态.若存在路径需求极大，导致其处于极限阻塞状态、流量趋于“零”，这些路径即为“阻塞零流”路径. “阻塞零流”路径虽然比其他更长的非“堵塞零流”路径疏解时间稍短，但由于其被用户选择最多、已承载最大车辆数而不能继续分担疏解流量、流量值趋于“零”；因此，在拥堵用户均衡时，同一OD对间所有非“阻塞零流”路径的疏解时间相等而且最大，并大于或等于“阻塞零流”路径(若存在)的疏解时间，若不存在“阻塞零流”路径，则同一OD对间的所有路径疏解时间相等.最终拥堵均衡状态下，疏解流量集中在较长路径上，较短路径由于承载更多需求(车辆数)，拥堵较严重，流量较小.考虑到实际路网不存在完全堵塞的路径，本文中的“阻塞零流”路径存在与否取决于具体应用时对其流量取值范围的定义.因此在实际路网中，若路网达到拥堵用户均衡状态时，所有路径均存在流量，且同一OD对间所有路径出行时间相等，这与Wardrop用户均衡原理^[1]不矛盾.

基于Wardrop用户均衡原理的假设得到拥堵用户均衡条件：在路网所有路段处于拥堵状态下，道路用户在完全信息情况下尽量地选择可用的最短路径，当路网处于拥堵均衡时，路网中同一OD间的所有非“阻塞零流”路径的疏解时间相等且最大的，且大于或等于“阻塞零流”路径(若存在)疏解时间.但在真实路网中，严格意义上的绝对“阻塞零流”不存在，因此拥堵用户均衡条件可进一步理解为：拥堵状态下，路网处于拥堵均衡时，同一OD对间所有路径疏解时间均相等.

2.2 拥堵系统最优均衡原理

在系统最优的静态均衡分配过程中，其前提假设为交通系统管理者期望看到的交通流分配结果，路网在管理者协调指挥下达到最优的一种状态.

静态拥堵交通流分配流量是拥堵状态下路网的疏解流量，从管理者的角度来看，整个拥堵网络疏解交通过程中所有用户的总疏解时间越小越好.因此，静态拥堵交通流分配的系统最优均衡原理定义为：在拥堵条件下，交通流量应该按照使得路网中总疏解时间最小的原则进行分配.

3 拥堵交通流均衡分配模型 3.1 拥堵用户均衡分配模型

1) 均衡分配模型.参考静态畅通交通流用户均衡分配的Beckmann模型^[1]，构建拥堵状态下的用户均衡分配模型为

$ \max :Z\left( X \right) = \sum\limits_a {\int_0^{{x_a}} {{t_a}} } (w){\rm{d}}w, $

(4)

$ {\rm{s}}.{\rm{t}}.\left\{ {\begin{array}{*{20}{c}} {\sum\limits_k {f_k^{rs}} = {q_{rs}},}\\ {f_k^{rs} \ge 0,}\\ {{x_a} = \sum\limits_r {\sum\limits_s {\sum\limits_k {f_k^{rs}} } } \delta _{a,k}^{rs}.} \end{array}} \right. $

(5)

其中：x_a为路段a的疏解流量；t_a为路段a的疏解时间；t_a(x_a)为路段a疏解时间函数；q_rs为OD对rs间的疏解流量；f_k^rs为OD对rs间路径k的疏解流量；δ_{a, k}^rs为路径-路段关联变量，如果路段a属于rs间路径k，值为1，否则值为0.

同时，为证明该模型与拥堵用户均衡原理的等价性与模型最优解的唯一性，引入：c_k^rs为rs间路径k的疏解时间；u_rs为拉格朗日乘子，也表示rs间拥堵均衡时的路径疏解时间.

2) 模型等价性证明.为证明用户均衡分配模型与用户均衡原理的等价性，构建拉格朗日函数为

$ L = Z\left( X \right) + \sum\limits_{rs} {{u_{rs}}} \left( {{q_{rs}} - \sum\limits_k {f_k^{rs}} } \right), $

(6)

根据K-T条件，∀k, r, s, 式(6)须满足

$ f_k^{rs}\frac{{\partial L}}{{\partial f_k^{rs}}} = 0,\frac{{\partial L}}{{\partial f_k^{rs}}} \le 0. $

(7)

对u_rs求偏导，可知$\frac{\partial L}{\partial u_{r s}}=q_{r s}-\sum\limits_{k} f_{k}^{rs}=0 \forall r$, s.

对OD对mn间路径l的疏解流量求偏导，得

$ \frac{{\partial L}}{{\partial f_l^{mn}}} = \frac{{\partial Z}}{{\partial f_l^{mn}}} + \frac{\partial }{{\partial f_l^{mn}}}\sum\limits_{rs} {{u_{rs}}} \left( {{q_{rs}} - \sum\limits_k {f_k^{rs}} } \right). $

(8)

其中$\frac{\partial Z}{\partial f_{l}^{m n}}=\sum\limits_{b \in L} \frac{\partial Z}{\partial x_{b}} \frac{\partial x_{b}}{\partial f_{l}^{m n}}$，

因为$\frac{\partial Z}{\partial x_{b}}=\frac{\partial}{\partial x_{b}} \sum\limits_{a} \int_{0}^{x_{a}} t_{a}(w) \mathrm{d} w=t_{b}$，$\frac{\partial x_{b}}{\partial f_{l}^{m n}}=\delta_{b, l}^{m n}$，

所以

$ \frac{{\partial Z}}{{\partial f_l^{mn}}} = \sum\limits_b {{t_b}} \delta _{b,l}^{mn} = c_l^{mn}, $

(9)

同时，由于$\frac{{\partial f_k^{rs}}}{{\partial f_l^{mn}}} = \left\{ \begin{array}{l} 1, \\ 0, \end{array} \right.\begin{array}{*{20}{c}}\; \; \; {{\rm{若\; }}m = r, n = s, l = k; }\\ {{\rm{其它}}{\rm{.}}} \end{array}$

所以，式(8)第二项为

$ \frac{\partial }{{\partial f_l^{mn}}}\sum\limits_{rs} {{u_{rs}}} \left( {{q_{rs}} - \sum\limits_k {f_k^{rs}} } \right) = - {u_{mn}}, $

(10)

由式(8)~(10)可知，$\frac{\partial L}{\partial f_{l}^{m n}}=c_{l}^{m n}-u_{m n}$.

因此，∀k, r, s, K-T条件式(7)可转化为

$ \left\{ {\begin{array}{*{20}{c}} {f_k^{rs}\left( {c_k^{rs} - {u_{rs}}} \right) = 0,}\\ {c_k^{rs} - {u_{rs}} \le 0.} \end{array}} \right. $

(11)

式(11)对路网中任一OD中所有路径均成立.由式(11)可知，当f_k^rs>0，则有c_k^rs=u_rs；当f_k^rs=0，则有c_k^rs≤u_rs.式(11)的实际意义可理解为:在同一OD对间，某条路径为非“阻塞零流”路径时，其拥有相等且最长的路径阻抗u_rs；当“阻塞零流”路径存在时，即若存在f_k^rs=0，其路径阻抗小于或等于最长路径阻抗u_rs，f_k^rs=0可理解为流量趋于“零”的这一类路径，这类路径由于阻抗相对较小，被用户选择最多，从而承载最大车辆数而不能继续分担和疏解流量、流量值趋于“零”.在实际拥堵路网中，严格意义上的完全“堵塞零流”路径是不存在的，即拥堵路网总满足f_k^rs>0，因此，式(11)也进一步表示拥堵用户均衡状态下同一OD对所有路径疏解时间均相等.从而，该模型K-T条件的实际意义与拥堵用户均衡原理是等价的，所以本文建立的静态拥堵交通流分配模型满足拥堵用户均衡分配.

3) 解的唯一性证明.拥堵状态下用户均衡分配模的优化目标函数式(4)，可转换最小化的目标函数为

$ \min :M = - Z = - \sum\limits_a {\int_0^{{x_a}} {{t_a}} } (w){\rm{d}}w. $

(12)

由于式(12)为凸函数，其约束条件式(5)为线性函数，所以优化模型(4)~(5)为凸规划问题.对于凸规划问题，假如其目标函数严格凸，则模型最优解具有唯一性.

目标函数的Hessian矩阵为

$ {\nabla ^2}M\left( X \right) = - {\nabla ^2}Z\left( X \right) = - \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{t_1}}}{{{\rm{d}}{x_1}}}}&{}&{}\\ {}&{\frac{{{\rm{d}}{t_2}}}{{{\rm{d}}{x_2}}}}&{}\\ {}&{}&{\frac{{{\rm{d}}{t_n}}}{{{\rm{d}}{x_n}}}} \end{array}} \right]. $

(13)

由于式(1)为单调递减函数，即$\frac{\mathrm{d} t_{n}}{\mathrm{d} x_{n}} < 0$ < 0，所以式(13)为正定矩阵，目标函数(12)为严格凸函数.因此，拥堵用户均衡分配模型的解具有唯一性.

3.2 拥堵系统最优分配模型

参考静态畅通交通流系统最优分配模型，构建静态拥堵系统最优分配模型为

$ \min :Z\left( X \right) = \sum\limits_a {{t_a}\left( w \right) \cdot {x_a}} , $

(14)

$ {\rm{s}}.{\rm{t}}.\left\{ {\begin{array}{*{20}{c}} {\sum\limits_k {f_k^{rs}} = {q_{rs}},}\\ {f_k^{rs} \ge 0,}\\ {{x_a} = \sum\limits_r {\sum\limits_s {\sum\limits_k {f_k^{rs}} } } \delta _{a,k}^{rs}.} \end{array}} \right. $

(15)

模型(4)~(5)与模型(14)~(15)约束条件相同.可以通过对目标函数式(14)的变形，将系统最优分配模型的优化目标(14)转化为用户均衡分配模型目标函数形式，其中

$ \begin{array}{l} \sum\limits_a {{t_a}} (w) \cdot {x_a} = \sum\limits_a {\int_0^{{x_a}} {\rm{d}} } \left[ {{t_a}(w) \cdot {x_a}} \right] = \\ \;\;\;\;\;\;\;\;\;\sum\limits_a {\int_0^{{x_a}} {\left[ {{t_a}(\omega ) + \omega \frac{{{\rm{d}}{t_a}(\omega )}}{{{\rm{d}}\omega }}} \right]{\rm{d}}\omega } } , \end{array} $

(16)

令

$ {t_a}\left( {{x_a}} \right) + \omega \frac{{{\rm{d}}{t_a}\left( {{x_a}} \right)}}{{{\rm{d}}{x_a}}} = T\left( {{x_a}} \right), $

则式(16)为

$ \sum\limits_a {{t_a}} (w) \cdot {x_a} = \sum\limits_a {\int_0^{{x_a}} {\left[ {T\left( \omega \right)} \right]{\rm{d}}\omega } } . $

由式(3)可知，T(x_a) < 0，因此，拥堵系统最优分配模型目标函数(14)可以转换为用户均衡分配模型目标函数形式，即

$ \max :Z\left( X \right) = \sum\limits_a {\int_0^{{x_a}} {\left[ { - T\left( \omega \right)} \right]{\rm{d}}\omega } } . $

4 求解算法

静态拥堵用户均衡分配模型可采用迭代加权法进行求解.算法可反复迭代所有拥堵路段的疏解流量而趋于均衡^[20].具体步骤：1)初始化.初始化路段阻塞疏解时间，按t_a⁰=t_{m, a}0计算，选择疏解时间最大的路径加载流量进行疏解(使拥堵路径逐渐畅通)，求得所有拥堵路段的疏解流量{x_a^l}，l=0. 2)更新疏解时间.根据新的路段疏解流量计算拥堵路段的疏解时间t_a^l=t_a(x_a^l). 3)计算附加疏解流量.根据更新后的疏解时间和OD疏解流量，选择疏解时间最大的路径进行全有全无分配，计算各路段的附加疏解流量{y_a^(l)，∀a∈A. 4)更新路段疏解流量.采用迭代加权法更新路段疏解流量：$\left\{x_{a}^{(l+1)}=x_{a}^{(l)}+\frac{1}{l}\left(y_{a}^{(l)}-x_{a}^{(l)}\right)\right\}$，∀a∈A. 5)检验精度.假如$\sqrt {\sum\limits_a {{{\left({x_a^{(l + 1)} - x_a^{(l)}} \right)}^2}} } /\sum\limits_a {x_a^{(l)}} \varepsilon $(ε为预设收敛迭代精度)，则最终路网各拥堵路段分配疏解流量为x_a^(l+1)；否则，l=l+1，返回第2步继续进行迭代.

5 算例分析

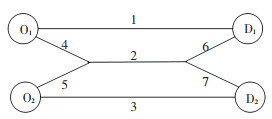
假设道路网络如图 1所示，由两对OD、4条路径组成. O₁D₁的分配流量是200，包含路径1(路段1)、路径2(路段4—2—6)；O₂D₂的分配流量是300，包含路径3(路段3)、路径4(路段5—2—7).各路段属性见表 1.

畅通路段阻抗函数与畅通路段车辆数计算公式分别为t_a(x_a)=t₀[1+0.15(x_a/c_a)⁴]，N_a(x_a)=x_a·t_a(x_a)；拥堵路段阻抗函数与拥堵路段车辆数计算公式分别为$\hat{t}_{a}\left(x_{a}\right)=t_{m a}\left(1+0.1 \hat{x}_{a} / c_{a}\right)^{-60}$，${\hat N_a}\left({{x_a}} \right) = {\hat x_a} \cdot {t_a}\left({{{\hat x}_a}} \right)$.本例中，带“^”上标的均表示拥堵状态，而且，假设所有路段的阻塞疏解时间为自由流的350倍，远小于无穷大，相应地定义，$\hat{x}_{a} \leqslant 34$时路段处于阻塞状态(阻塞疏解时间取值越大，阻塞状态流量越趋近于0).

路段流量的分配结果见表 2.静态畅通与拥堵用户均衡分配结果对比见表 3；静态拥堵用户均衡与拥堵系统最优分配结果对比见表 4.

在相同的OD分配流量下，静态畅通交通分配与拥堵交通分配含义不同.

以O₁D₁为例(包含路径1、2)，OD分配流量为200，在静态畅通交通分配中，分配流量意味着OD对之间的需求流量为200.其中路径1需求流量为181，路径2需求流量为19，均小于两条路径通行能力，此时两条路径车辆数较少，路径1、2均处于畅通状态.分配结果体现了畅通状态下，需求流量可以完全分配至路段上，且集中在较短路径上(路径1).

在静态拥堵交通分配中，分配流量意味着OD对之间的疏解流量为200.其中路径1疏解流量为89，路径2疏解流量为111，此时两条路径车辆数较多，路径需求远大于通行能力，同时路径的疏解流量也远小于路径的需求(需求大于疏解流量的部分在起点排队，未进入路网)，两条路径的密度均大于通行能力时的临界密度，处于拥堵状态.分配结果体现了拥堵状态下，过多的需求选择较短路径(路径1)，反而导致路径1流量下降，较少的需求选择较长路径(路径2)，从而路径2流量相对较大.这符合实际拥堵路网中可观测到的流量现象，即在拥堵状态下，较短路径承担过多的需求，反而更加拥堵、流量较小，较长路径承担需求相对较少，相对畅通、流量较大.这是因为，拥堵状态下大量用户对较短路径的选择，会导致较短路径的密度增加、速度减小、流量减少.较长路径由于被相对少量的用户选择，密度相对较小，速度较大，流量较大，分配结果也意味着拥堵状态下较长路径(路径2)单位时间内疏解的车辆数更多.同理，O₂D₂以及路径3、路径4也符合上述分析结果.因此，拥堵用户均衡分配可以合理描述路段全拥堵时路段流量实际通过情况.

由表 4可知，两对OD的总分配流量为500，拥堵用户均衡状态时，路网中所有用户的平均疏解时间242.82；路网处于系统最优状态时，路网中所有用户的平均疏解时间242.59.在拥堵用户均衡状态下，路网所有路段均拥堵，同一OD对所有出行者疏解时间均相等.在路网分配相等的OD流量下，拥堵用户均衡状态比拥堵系统最优状态路网承载的总车辆数更多，说明用户均衡状态下，路网更为拥挤.拥堵系统最优状态时，路网中所有用户总疏解时间最小，用户的平均疏解时间更短，路段更畅通，路网状态最佳.因此，拥堵用户均衡分配模型和拥堵系统最优分配模型分配结果分别满足拥堵用户均衡原理与拥堵系统最优原理.

从交通需求角度，当超饱和交通需求处于稳定、长时间持续的情况下，局部区域可形成稳定的完全拥堵状态.在这种完全拥堵的部分区域内，可采用本文提出的模型进行交通分配.完全拥堵状态的静态分配模型，可以保留静态模型的基本特点(易于计算、易于理解、数学严格性、相对稳定)，也能克服传统静态分配模型的缺点(只适用于畅通状态)，同时刻画拥堵空间蔓延下的稳定状态.然而，实际路网中通常处于半拥堵状态，即部分路段畅通、部分路段拥堵.这是由于目前的超饱和交通需求具有非稳定、持续时间短的特点.因此，半拥堵状态可以看作是拥堵蔓延发生或消散的中间发展状态.如何将完全拥堵的静态交通分配模型与完全畅通的静态交通分配模型相结合，去分析半拥堵状态交通流分配问题是未来的研究方向.需要强调的是，本文提出的拥堵交通流分配模型可作为半拥堵静态交通流分配的核心部分之一.

6 结论

1) 针对传统静态交通流分配不能有效解决拥堵条件下交通流分配问题，基于拥堵路段阻抗和完全信息条件，提出拥堵条件下的用户均衡与系统最优原理，构建静态拥堵用户均衡模型和拥堵系统最优模型，证明拥堵用户均衡模型与拥堵用户均衡原理等价性与模型最优解的唯一性，给出拥堵用户均衡模型的求解算法.

2) 算例表明，拥堵用户均衡分配模型与拥堵系统最优分配模型可以合理描述拥堵用户均衡原理与系统最优均衡原理，且拥堵用户均衡分配模型可以合理描述路网处于全拥堵状态下各路段实际通过的流量.

3) 全拥堵交通流分配模型有助于分析路网本身特性，可应用于由拥堵蔓延导致的局部全拥堵区域，可作为半拥堵静态交通流分配的核心部分之一.同时，静态拥堵交通流分配模型丰富了传统静态交通流分配方法，对于分析大城市拥堵路网的交通特征具有重要的理论与实际意义.