2. 重庆市轨道交通建设办公室, 重庆 400014
2. Chongqing Rail Transit Construction Office, Chongqing 400014, China
直线电机轮轨交通采用直线感应电机LIM(linear induction motor)进行非黏着牵引和制动,由钢轮钢轨支承和导向.直线感应电机的定子(初级线圈)固定在车辆底部,常称作直线电机;转子(次级线圈)固定在轨道上,常称作感应板.其车辆具有爬坡能力强、曲线通过性好、车辆限界小、轴重轻等优点,可增大线路限制坡度、减小线路最小曲线半径、降低隧道断面尺寸和桥梁荷载,使选线更灵活,进而降低工程造价.此外,行车时动力性能好、对车辆构件和轨道结构的损耗小,使得运营过程中车辆安全平稳、车辆和线路的养护维修工作量少、产生的振动噪声小,故运营费用低.适合在地形条件复杂、建筑物密集、轨道交通线网密布和地下空间资源紧张的城市中应用.但目前规范中对该种轨道交通线路参数匹配的规定仍与传统轮轨地铁基本一致[1],不能充分发挥其选线灵活的优势.
国内已建立了单节车辆-线路动力学模型,并对直线电机轮轨交通线路动力响应进行了初步研究,而目前国外相关研究较少.文献[2]建立了具备径向转向架的直线电机车辆-线路动力学模型,通过改变曲线参数,对线路参数的合理匹配进行了研究;文献[3]分析了曲线参数对车辆动力响应的效应;文献[4]研究了轨道不平顺对系统动力响应的影响;文献[5]基于车辆-轨道横垂向耦合动力学模型,对轨道几何不平顺影响下的系统动力学特性进行了研究;文献[6]研究了直线电机隔振优化;文献[7]运用SIMPACK多体动力学软件和SIMULINK联合仿真方法,基于车辆-线路动力学模型,分析了直线电机对车辆系统动力学性能的影响.文献[8]通过建立考虑直线电机电磁力的车辆-线路模型,模拟了车辆在通过地面和高架桥这两种敷设方式线路时的动力学响应,分析了在垂向电磁力影响下车辆运行在高架桥上的安全性和稳定性.文献[9]分析了直线电机与感应板间气隙对车辆的动力学效应;文献[10]研究了纵断面线路参数、车速等对系统动力响应的影响.
目前有关直线电机轮轨交通的研究,主要侧重于单节车辆的垂向动力学、横向动力学及横垂向动力学,而对多节编组列车动力学模型的研究很少.国内外相关动力学模型中,均将垂向电磁力简化为弹性元件,规定气隙(直线电机与感应板之间的间隙)为垂向电磁力大小的唯一决定因素,而未考虑车速对电磁力的影响.对车速、线路参数、轨道不平顺共同作用下的动力响应变化规律缺乏研究,致使对规范中线路参数匹配、车辆限界的修改缺乏依据.
本文以首都机场线列车和线路参数[11-12]为基础,建立了直线电机轮轨交通列车-线路动力学模型,列车所受垂向电磁力大小随气隙和车速的变化而时刻改变.对东直门站到三元桥站地下区间的列车-线路系统进行了动力学仿真计算,其中计算所得车体加速度与现场采集数据相吻合.
本文分析了直线电机垂向电磁力、曲线半径、超高、列车时速、轨道不平顺对系统动力响应的影响,为优化规范中线路参数匹配和车辆限界提供了理论依据.
1 模型建立建立了直线电机列车-线路动力学模型,每节车辆的车体、转向架均具有6个自由度(伸缩、横移、沉浮、侧滚、摇头、点头),轮对具有5个自由度(伸缩、横移、沉浮、侧滚、摇头).轮轨法向力由Hertz非线性弹性接触理论确定,纵向及横向蠕滑力由经Johnson-Vermeulen理论修正过的Kalker理论确定. 图 1为每节车的动力学模型示意图.

|
图 1 车辆动力学模型示意图 Fig. 1 Schematic diagram of vehicle dynamics model |
采用架悬式电机悬挂方式,将车载直线电机与转向架直接连接.首都机场线车辆的基本参数如下:转向架轴距为1.9 m,转向架质量为4.096 t,转向架中心距为12 m,轴重为10 t,轮对内侧距为1.356 m,车轮直径为0.66 m,一系悬挂横向跨距为1.18 m,二系悬挂横向跨距为1.677 m,垂向减振器横向跨距为2.388 m,旁承横向跨距为1.18 m,车体质量为25.5 t,车体长度为16.5 m,车体宽度为2.5 m,车辆高度为3.15 m,车辆底板离轨面高度为0.8 m,车钩缓冲器容量为76 kJ,车钩缓冲器最大行程为0.14 m.
本文模型采用美国六级轨道不平顺谱实现了轨道随机不平顺.模型中同时设置了高低、水平、轨向、轨距这4种轨道不平顺类型,其不平顺峰值分别为8.6、8.2、8.6、8.2 mm,以4种不平顺组成的复合不平顺来模拟首都机场线的轨道不平顺情况.
直线电机与感应板之间存在三向相互作用力:纵向力为列车驱动力,其与多种阻力的合力对列车的作用效果由列车在行驶过程中的纵向加速度表示,不单独设置纵向电磁力;垂向力为吸引力,给列车提供竖直向下的作用力,电机结构确定后,垂向电磁力主要受列车运行速度和气隙影响;横向力相对较小,本模型中横向电磁力取1 kN定值.
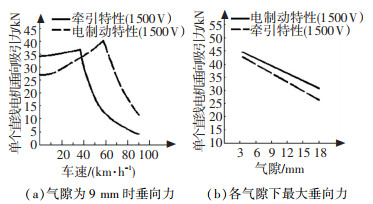
首都机场线列车所用直线电机的垂向电磁力特性[12]可简化成图 2中的曲线.
|
图 2 直线电机垂向电磁力特性 Fig. 2 Vertical electromagnetic force characteristics of LIM |
本文假设在任意车速下,随着气隙变化,垂向电磁力的变化趋势与图 2(b)中最大垂向力的变化趋势相同,故可将垂向力简化为
| $F_{\mathrm{d}}=F_{\mathrm{d} 0}-\beta_{\mathrm{d}}\left(z_{\mathrm{ag}}-z_{\mathrm{ag} 0}\right), $ | (1) |
| $F_{\mathrm{b}}=F_{\mathrm{b} 0}-\beta_{\mathrm{b}}\left(z_{\mathrm{ag}}-z_{\mathrm{ag} 0}\right). $ | (2) |
式中:Fd为牵引工况下单电机的垂向吸引力,kN;Fd0为9 mm气隙时牵引工况下单电机的垂向吸引力,kN;Fb为制动工况下单电机的垂向吸引力,kN;Fb0为9 mm气隙时制动工况下单电机的垂向吸引力,kN;zag为列车行驶时的瞬时气隙,mm;zag0=9 mm为北京机场线列车直线电机初始气隙;βd=1.11 kN/mm为牵引工况下每增大1 mm气隙引起的垂向力减小量;βb=0.96 kN/mm为制动工况下每增大1 mm气隙引起的垂向力减小量.
2 复合线路动力响应首先对东直门站至三元桥站区间内车-线动力系统进行仿真,并采集实际运行车体横、垂向加速度的时程曲线,平纵断面线路参数见表 1、2.首都机场线列车全长67.7 m,实行4节车辆编组,规定头车为1号车辆,则2号与3号车辆间车钩的纵向中点为列车中心点.表中平面曲线为凹曲线时的转角为正,凸曲线时为负;上坡坡度为正,下坡坡度为负.
| 表 1 线路平面参数 Tab. 1 Plane parameters of lines |
| 表 2 线路纵断面参数 Tab. 2 Parameters of longitudinal profile |
由表 1、2可知,列车中心点行程(简称行程)为120.6~421.6 m时平面线路变化较剧烈,为180 m的小半径曲线段;行程为2 440.1~2 622.8 m、2 829.5~2 913.5 m时纵断面线路变化较剧烈,坡度代数差可达30‰.除此之外线路变化均较缓.
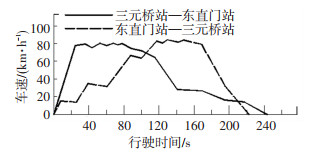
基于目前首都机场线列车实际运行曲线图[13],将东直门站—三元桥站区间列车运行曲线进行简化,得到图 3.因首都机场线列车由4节动车组成,故每节车辆纵向速度均按图 3中速度时程曲线设置.
|
图 3 列车运行曲线 Fig. 3 Train operation curve |
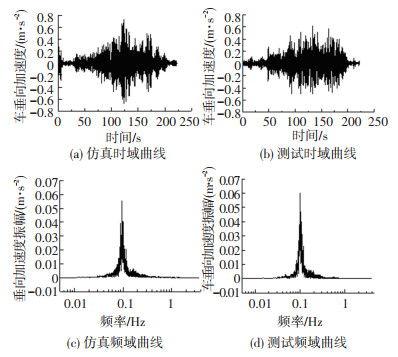
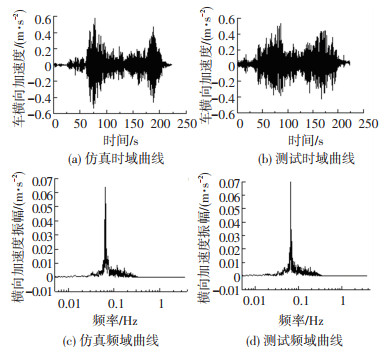
将加速度传感器固定在列车各节车辆的地板上,利用数据采集系统同步采集4节车的横、垂向加速度,得到各车辆实际运行于东直门站—三元桥站区间时的加速度变化时程曲线.采用二阶巴特沃斯低通滤波器进行滤波,临界频率设为150 Hz.采集数据与仿真结果在时域与频域两方面均吻合.以图 4、5为例,可知在变速行驶过程中,车体垂向振动的主频率约为0.1 Hz,横向振动的主频率约为0.06 Hz.
|
图 4 1号车辆垂向加速度 Fig. 4 Vertical acceleration of head vehicle |
|
图 5 1号车辆横向加速度 Fig. 5 Lateral acceleration of head vehicle |
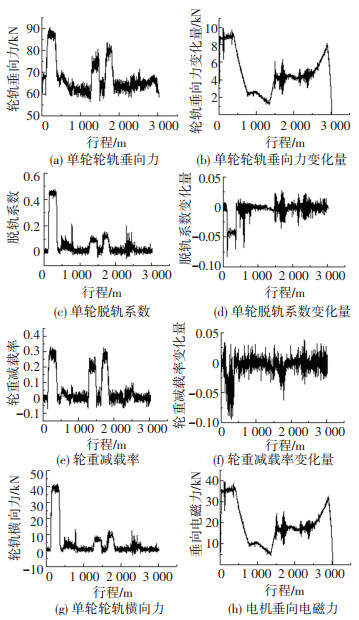
计算发现,各节车辆经过线路同一位置时的动力响应值差别很小. 图 6中展示了1号车的1号轮对和1号直线电机的动力响应变化规律.按列车是否受垂向电磁力作用,计算得两个工况下的系统动力响应,将考虑垂向电磁力的计算结果与不考虑垂向电磁力的计算结果相减,得动力响应变化量曲线.受垂向电磁力影响较大的动力响应变量为轮轨垂向力、脱轨系数、轮重减载率,几乎不受影响的为车体横、垂向加速度.当列车行驶至东直门站附近平面小半径曲线段时轮轨力、脱轨系数、轮重减载率均显著增大,脱轨系数减小量和轮重减载率减小量均显著增大.
|
图 6 动力响应时程曲线 Fig. 6 Time history curve of dynamic response |
对比图 6(b)、6(h),单轮轮轨垂向力变化量约为其所在转向架上直线电机垂向电磁力的1/4,即每台直线电机的电磁力可近似成被平均分配在其所连接转向架对应的4个车轮上.因电机垂向电磁力给列车提供向下的吸引力,与没有垂向电磁力的工况相比,会使轮轨垂向力变大,致使脱轨系数和轮重减载率均变小,以增大列车运行安全性.垂向电磁力会使各轮对与左右轨之间的蠕滑导向力重新分配,使左右轮轨垂向力重新分配、横向力减小.经仿真发现电磁力导致的左右轮轨垂向力重新分配量、横向力减小量相对较小,故将其忽略,可大致确定脱轨系数和轮重减载率的减小量,即
| $\Delta T=\frac{Q}{P}-\frac{Q}{P+\Delta P}=\frac{Q(\Delta P)}{P(P+\Delta P)}=\frac{T(\Delta P)}{P+\Delta P}, $ | (3) |
| $\begin{array}{l} \Delta D = \frac{{\left| {{P_z} - {P_y}} \right|}}{{{P_z} + {P_y}}} - \frac{{\left| {{P_z} - {P_y}} \right|}}{{{P_z} + {P_y} + 2\Delta P}} = \\ \frac{{\left| {{P_z} - {P_y}} \right|(2\Delta P)}}{{\left( {{P_z} + {P_y}} \right)\left( {{P_z} + {P_y} + 2\Delta P} \right)}} = \\ \frac{{D(2\Delta P)}}{{{P_z} + {P_y} + 2\Delta P}} \end{array} $ | (4) |
式中:ΔT为脱轨系数减小量;Q为单轮轮轨横向力,kN;P为单轮轮轨垂向力,kN;ΔP为电磁力引起的单轮轮轨垂向力增量,kN;T为无电磁力时的脱轨系数;ΔD为轮重减载率减小量;Pz为左轮轮轨垂向力,kN;Py为右轮轮轨垂向力,kN;D为无电磁力时的轮重减载率.
如图 6(d)、6(f)所示,脱轨系数和轮重减载率只在东直门站附近平面小半径曲线段显著降低.由式(3)、(4)可知,T和ΔP对ΔT的影响较大,D和ΔP对ΔD的影响较大.小半径曲线较易使T和D显著增大,多数情况下P的增速相对较慢,且ΔP变化量小,故易使ΔT和ΔD增大.高车速较易增大T和D,但会减小ΔP.故车通过小半径曲线段时垂向电磁力易导致脱轨系数和轮重减载率的显著消减.
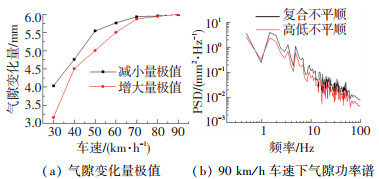
3 单一线路动力响应经仿真得可知,曲线地段线路参数变化对气隙影响很小,气隙受轨道不平顺和车速影响显著. 图 7为直线地段车速大小、轨道不平顺对气隙的影响.
|
图 7 气隙变化规律 Fig. 7 Variation regularity of air gap |
轨道垂向不平顺和感应板垂向不平顺共同决定了静态气隙的大小,列车在行驶中所受轮轨垂向力主要由轨道垂向不平顺影响,致使直线电机产生较大垂向振动,静态气隙与电机垂向振动位移叠加,形成了动态气隙.应避免出现因动态气隙太小而导致直线电机与感应板剐蹭,以及气隙太大导致牵引效率显著降低.由图 7(a)可知,气隙变化量小于6 mm,故初始静态气隙为9 mm时,动态气隙始终能较好满足安全性和牵引效率的要求.
从图 7(b)可知,同时考虑4种不平顺类型的复合不平顺影响下,气隙峰值频段为1.2~2 Hz,因车速为90 km/h,故波长段为12.5~20.8 m的线路不平顺激扰对气隙影响显著,建议在养护维修时采用10 m弦长法,对轨道垂向不平顺和感应板垂向不平顺进行重点管理.
基于控制变量法设置变量工况,研究车速、曲线半径、超高对列车动力响应的影响规律.针对各个变量工况,从4节车的全部计算结果中提取各类动力响应变量的最大值,研究工况变量对动力响应变量最大值的影响规律.经分析可知:1)脱轨系数、轮重减载率、轮轨横向力、轮轨垂向力、车体横向加速度、车体横向位移这6个动力响应变量同时受曲线半径、超高和车速的显著影响;2)车体垂向加速度与车速的平方成正比关系;3)过超高下随车速增大,6类动力响应缓慢减小,欠超高下随车速增大,6类动力响应快速增大;4)欠超高下随半径减小,6类动力响应快速增大,过超高下随半径减小,6类动力响应缓慢减小.因由脱轨系数和轮轨横向力可确定轮轨垂向力,故合理的线路条件只需同时满足5类动力响应不超规范限值. 图 8为动力响应变量最大值与车速、曲线半径、超高之间的关系曲线,缓和曲线长度统一设为50 m.

|
图 8 动力响应最大值规律 Fig. 8 Regularity of maximum dynamic response |
设置15个车速变量值:20、25、30、35、40、45、50、55、60、65、70、75、80、85、90 km/h;设置20个曲线半径变量值:300、350、400、450、500、550、600、650、700、750、800、850、900、950、1 000、1 200、1 500、2 000、2 500、3 000 m;设置32个超高变量值:5、10、15、20、25、30、35、40、45、50、55、60、65、70、75、80、85、90、95、100、105、110、115、120、125、130、135、140、145、150、155、160 mm.经排列组合可设置9 600个工况进行仿真,对全部工况的各动力响应变量最大值分别进行拟合,即
| $T_{\max }=0.005\;9\left(\frac{v^{2}}{R}-\frac{h}{8.7}\right)^{2}+0.000\;21\left(\frac{h v^{2}}{R}\right)+0.05, $ | (5) |
| $D_{\max }=0.001\;9\left(\frac{v^{2}}{R}-\frac{h}{10}\right)^{2}+0.053, $ | (6) |
| $Q_{\max }=0.63\left(\frac{v^{2}}{R}-\frac{h}{11}\right)^{2}+5.15, $ | (7) |
| $a_{\max }=0.008\;3\left(\frac{v^{2}}{R}-\frac{h}{11.3}\right)^{2}+0.11, $ | (8) |
| $s_{\max }=0.32\left(\frac{v^{2}}{R}-\frac{h}{10.8}\right)^{2}+31. $ | (9) |
式中:Tmax为脱轨系数最大值;v为车速,km/h;R为曲线半径,m;h为超高,mm;Dmax为轮重减载率最大值;Qmax为单轮轮轨横向力最大值,kN;amax为车体横向加速度最大值,m/s2;smax为车体横向位移最大值,mm.
当v为20~70 km/h、R为100~250 m(即低速过小半径曲线段),动力响应值仍符合拟合公式.由式(5)~(9)确定均衡超高,即
| $\begin{aligned} h_{\mathrm{q}}=& \frac{(10.3+10+11+11.3+10.8)}{5} \times \frac{v^{2}}{R}=\\ & \frac{10.7 v^{2}}{R}, \end{aligned} $ | (10) |
式中hq为均衡超高,mm.
已知均衡车速和曲线半径,由式(10)确定的均衡超高约为由规范所确定均衡超高的90.7 %.规范中确定均衡超高时将车体简化为质点,对质点进行力学计算.而本文模型与实际车辆更接近,其弹性悬挂系统使均衡超高减小.悬挂系统和电磁垂向吸引力可减小曲线处列车与轨道间的动力冲击.基于式(5)~(9)可由v、R和h确定5类动力响应变量的最大值,综合考虑这5类动力响应变量的限值,可总结出:1)在已知v和R的条件下确定超高合理取值范围;2)在已知R和h的条件下确定允许通过的车辆最大时速;3)在已知v和h的条件下确定最小曲线半径;4)欠超高、过超高、可设最大超高的允许值.由式(10)可基于v和R确定h的最佳值(均衡超高),但实际通过同一条曲线段的各列车时速会有差异,进而产生过超高或欠超高.故需基于均衡超高、过超高允许值、欠超高允许值来确定超高取值范围,进而可确定实际车速与均衡车速差值的允许范围.与规范相比发现,过超高允许值、欠超高允许值、最大超高、各半径对应的最大车速均显著增大,各车速下的最小曲线半径明显减小.随着v、h增大或R减小,脱轨系数和车体横向加速度较易超过限值,说明式(5)和式(8)对线路参数设置的影响显著.所得拟合公式可为车速、曲线半径、超高之间取值的合理匹配提供理论依据.
因超高影响,列车在曲线地段上会产生明显的侧滚角,悬挂系统的弹性效应会使车体侧滚角小于超高角,但轨道不平顺会增大侧滚角,经仿真发现侧滚角峰值约等于超高角.本文提出曲线段车体横向位移最大值与车速、曲线半径、超高的关系公式,并规定车体侧滚角最大值为超高角,可为曲线段合理车辆限界的确定提供理论依据,从而合理确定曲线段线路间距加宽值、曲线站台与车辆轮廓线间隙取值、曲线站台最小半径、隧道和桥梁断面尺寸.在同时满足Tmax、Dmax、Qmax、amax不超限的前提下,基于式(9)可确定不同速度与线路匹配下,曲线段车辆限界的相关尺寸、线路加宽值、站台间隙,并发现计算结果小于规范中相关尺寸.
对比有无电磁力的各动力响应计算结果,发现脱轨系数和轮重减载率因垂向电磁力的施加而显著减小,如图 9所示.当车速较大时,半径越小则动力响应消减作用越强;当半径较大时,低车速使动力响应消减作用更加显著.

|
图 9 垂向电磁力影响下动力响应减小量的最大值 Fig. 9 Maximum of dynamic response reduction under vertical electromagnetic force |
1) 垂向电磁力对脱轨系数和轮重减载率有一定消减作用,进而提高车辆的曲线通过能力.曲线半径较小时,消减作用更显著.
2) 所提出各动力响应变量最大值拟合公式可为车速、曲线半径、超高之间取值的合理匹配提供理论依据.与规范相比,过超高允许值、欠超高允许值、最大超高、某曲线半径下允许最大车速均显著增大,各车速下的最小曲线半径减小,均衡超高约减小10 %.
3) 所提出曲线段车体横向位移最大值拟合公式可为曲线段合理车辆限界的确定提供理论依据,从而合理确定曲线段线路间距加宽值、曲线站台与车辆轮廓线间隙取值、曲线站台最小半径、隧道和桥梁断面尺寸.
| [1] |
中华人民共和国住房和城乡建设部.城市轨道交通直线电机牵引系统设计规范: CJJ 167—2012[S].北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for design of urban rail transit by linear motor: CJJ 167—2012[S]. Beijing: China Building Industry Press, 2012 |
| [2] |
赵金顺, 万传风, 张勇, 等. 直线电机轨道交通车线耦合模型的动力响应研究[J]. 铁道学报, 2006, 28(5): 129. ZHAO Jinshun, WAN Chuanfeng, ZHANG Yong, et al. Research on dynamic response of coupled model between vehicle and track for LIM track transportation[J]. Journal of the China Railway Society, 2006, 28(5): 129. DOI:10.3321/j.issn:1001-8360.2006.05.024 |
| [3] |
龙许友, 魏庆朝, 赵金顺. 直线电机地铁车辆曲线通过建模与仿真[J]. 系统仿真学报, 2007, 19(13): 3105. LONG Xuyou, WEI Qingchao, ZHAO Jinshun. Modeling and simulation of curve negotiation of linear metro vehicle[J]. Journal of System Simulation, 2007, 19(13): 3105. DOI:10.3969/j.issn.1004-731X.2007.13.054 |
| [4] |
龙许友, 魏庆朝, 冯雅薇, 等. 轨道不平顺激励下直线电机车辆/轨道动力响应[J]. 交通运输工程学报, 2008, 8(2): 9. LONG Xuyou, WEI Qingchao, FENG Yawei, et al. Dynamic response of linear metro vehicle/track excited by track irregularity[J]. Journal of Traffic and Transportation Engineering, 2008, 8(2): 9. DOI:10.3321/j.issn:1671-1637.2008.02.003 |
| [5] |
熊嘉阳, 曹亚博, 吴磊, 等. 轮轨纵向几何不平顺对直线电机地铁车辆动态行为的影响[J]. 西南交通大学学报, 2015, 50(6): 1074. XIONG Jiayang, CAO Yabo, WU Lei, et al. Effect of longitudinal geometric irregularities of wheel and rail on dynamic behavior of metro vehicle driven by linear motor[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1074. DOI:10.3969/j.issn.0258-2724.2015.06.014 |
| [6] |
宗凌潇, 马卫华, 罗世辉. 直线电机地铁车辆电机的隔振优化分析[J]. 机械工程学报, 2015, 51(18): 119. ZONG Lingxiao, MA Weihua, LUO Shihui. Optimization analysis of vibration isolation of linear motor of metro vehicles[J]. Chinese Journal of Mechanical Engineering, 2015, 51(18): 119. DOI:10.3901/JME.2015.18.119 |
| [7] |
胡彦.直线电机地铁车辆动力学性能研究[D].成都: 西南交通大学, 2009 HU Yan. Research on dynamic performance of LIM vehicle[D]. Chengdu: Southwest Jiaotong University, 2009. DOI: 10.7666/d.y1573405 |
| [8] |
顾戌华, 夏禾, 郭薇薇. 直线电机列车-桥梁系统动力分析[J]. 振动工程学报, 2008, 21(6): 608. GU Xuhua, XIA He, GUO Weiwei. Dynamic analysis of LIM train-bridge system[J]. Journal of Vibration Engineering, 2008, 21(6): 608. DOI:10.3969/j.issn.1004-4523.2008.06.012 |
| [9] |
魏庆朝, 夏景辉, 臧传臻, 等. 气隙对直线电机地铁系统动力响应的影响[J]. 交通运输工程学报, 2017, 17(6): 10. WEI Qingchao, XIA Jinghui, ZANG Chuanzhen, et al. Influence of air gap on dynamic response of LIM metro system[J]. Journal of Traffic and Transportation Engineering, 2017, 17(6): 10. DOI:10.3969/j.issn.1671-1637.2017.06.002 |
| [10] |
魏庆朝, 臧传臻, 聂鑫路, 等. 纵断面线路参数对直线电机列车的动力影响[J]. 铁道工程学报, 2018, 35(1): 42. WEI Qingchao, ZANG Chuanzhen, NIE Xinlu, et al. Dynamic influence of profile parameters on LIM train[J]. Journal of Railway Engineering Society, 2018, 35(1): 42. DOI:10.3969/j.issn.1006-2106.2018.01.008 |
| [11] |
李妙迪, 余乐, 邢爱东, 等.北京市轨道交通首都机场工程施工图设计第二篇线路[Z].北京: 北京市市政工程设计研究总院, 2007 LI Miaodi, YU Le, XING Aidong, et al. Capital airport line design[Z]. Beijing: Beijing General Municipal Engineering Design & Research Institute Co., Ltd., 2007 |
| [12] |
CRC-庞巴迪联合体.北京首都国际机场工程直线电机车辆技术规格书[Z].北京: 北京市市政工程设计研究总院, 2006
|
| [13] |
崔霆锐, 宗立明, 李熙, 等. 北京地铁机场线直线电机国产化应用研究[J]. 电机与控制应用, 2016, 43(1): 35. CUI Tingrui, ZONG Liming, LI Xi, et al. Localization research on LIM for the airport line of Beijing subway[J]. Electric Machines & Control Application, 2016, 43(1): 35. DOI:10.3969/j.issn.1673-6540.2016.01.007 |
 2019, Vol. 51
2019, Vol. 51


