随着地铁信号系统的发展,列车自动驾驶系统已成为保证列车运行控制系统高效运行的关键环节.列车自动驾驶系统以参考速度曲线作为速度跟踪控制的依据[1-2],参考速度与列车实际运行能力间的偏差会直接影响自动驾驶系统的速度控制效果.目前对地铁列车速度的仿真计算模型大多采用传统大铁路列车使用的牵引计算方法[3-4],列车受力包括运行阻力和和列车施加的牵引、制动力,其中牵引/制动力按列车牵引/制动特性曲线取值,列车运行阻力(包括基本运行阻力和线路附加阻力)通常采用根据大量试验总结得到的经验公式计算[5-9].对于线路附加阻力的计算,目前发展出单质点、多质点和均质棒三种模型.根据既有研究结果,均质棒模型具有最优的计算精度[10-12].基于常规地铁列车仿真计算模型也有一些扩展研究,文献[13]考虑不同信号闭塞方式和列车间相互作用,针对多列车运行场景进行了仿真研究;文献[14]在计算列车运行速度曲线计算中考虑了牵引和制动的加载和卸载过程;文献[9]考虑工程设计限制,构造用于速度控制的仿真模型.在上述列车运行计算模型中,均将向列车施加的控制力指令等同于车辆实际实现的控制力,该假设忽略了地铁列车牵引/制动系统对控制力指令的“缓变式”处理过程以及车辆控制力产生的动态过程,给列车参考速度的仿真计算带来偏差.本文基于已有的地铁列车牵引计算模型,考虑地铁列车牵引/制动系统对控制指令的冲击限制处理及牵引/制动系统的动态响应过程,构造改进模型来提高列车参考速度仿真精度.
1 地铁列车速度仿真的常规模型地铁列车运行速度受到多种因素影响,通常根据列车受力分析,将这些因素归纳为车辆自身施加的控制力、基本阻力、线路附加阻力,列车加速度atrain和列车速度vtrain分别表示为
| $a_{\text {train }}=\left(F_{\text {conmand }}-W_{\text {basic }}-W_{\text {line }}\right) / M_{\text {train }}^{\prime}, $ | (1) |
| $\mathrm{d} v_{\text {train }} / \mathrm{d} t=a_{\text {train }}. $ | (2) |
其中Fcommand、Wbasic、Wline分别为列车自身施加的控制力、基本阻力、线路附加阻力;Mtrain′为列车动态质量,Mtrain′=Mtrain+Minertia,其中Mtrain为列车静态质量,Minertia为列车惯性质量.
列车控制力根据运行工况的不同(牵引或制动),分别由牵引或制动系统通过自身的反馈控制过程来实现,控制力的幅值受到列车牵引/制动特性的约束.基本阻力按戴维斯公式计算,线路附加阻力包括坡道附加阻力和曲线附加阻力,采用均质棒模型,将列车视为质量按长度均匀分配的质量带,按列车长度在线路上的分布来计算[3-4].
常规模型通常采用作用力作为列车运行参考速度的控制量,而地铁列车的牵引/制动控制系统一般以加速度作为控制量进行处理,将式(1)中的合力方程转变为加速度的形式,可表示为
| $a_{\text {train }}=a_{\text {command }}-d_{\text {basic }}-d_{\text {line }}. $ | (3) |
式中acommand、dbasic、dline分别为要求列车实现的指令加速度、基本阻力减速度、线路附加阻力减速度.其中阻力减速度及线路附加阻力减速度计算公式[3-4]分别为
| $d_{\mathrm{basic}}=\left(c_{0}+c_{1} v_{\mathrm{train}}+c_{2} v_{\mathrm{train}}^{2}\right) / M_{\mathrm{train}}^{\prime}, $ | (4) |
| $d_{\text {line }}=M_{\text {train }} g\left(\omega+\frac{600}{R}\right) / M_{\text {train }}^{\prime}. $ | (5) |
式中c0、c1、c2为非负常数项;g为重力加速度;ω、R分别为列车在当前位置按车长计算的平均坡道千分度和平均曲线半径.
由式(1)~(5)可知,由于基本阻力减速度和线路附加阻力减速度的计算方法较为成熟,列车速度的计算精度主要受指令加速度处理过程的影响.在常规模型中,对要求列车实现的指令加速度acommand、列车牵引/制动控制系统要实现的目标加速度atarget、列车牵引/制动系统通过控制实现的响应加速度aresponse不作区分,均等同于指令加速度,即有
| $a_{\text {command }}=a_{\text {target }}=a_{\text {response }}. $ | (6) |
考虑从指令加速度acommand到目标加速度atarget的冲击限制处理过程,以及从目标加速度atarget到响应加速度aresponse的牵引/制动动态响应过程,构造包括冲击限制模型和牵引/制动响应模型的改进模型.
2.1 冲击限制模型地铁列车牵引/制动系统的目标加速度atarget对时间的变化率为冲击率(jerk),对冲击率的约束称为冲击限制.冲击率关系到列车运行的稳定性和舒适度,影响地铁列车的运行质量.文献[15]要求列车牵引/制动控制系统应达到的冲击限制为1 m/s3[15],实际地铁项目中的车辆招标文件通常要求列车在牵引和制动(包含常用制动、快速制动和保持制动)时的冲击率不大于0.75 m/s3[16].列车牵引/制动控制系统可将“阶跃式”的加速度指令按照列车冲击限制要求转换为“缓变式”的加速度指令[17].
令atarget(t-Δt)为上一控制周期满足冲击限制约束的目标加速度,在改进模型中进行冲击限制约束的目标是使当前周期目标加速度atarget(t)满足列车冲击限制要求,即
| $\left|a_{\text {target }}(t)-a_{\text {target }}(t-\Delta t)\right| / \Delta t \leqslant \eta_{\text {jerk }, \text { max }}. $ | (7) |
式中ηjerk, max为列车最大冲击率限制值.
在进行冲击限制处理时,令âtarget(t)=acommand(t).若âtarget(t)-atarget(t-Δt)/Δt≤ηjerk, max,则atarget(t)=âtarget(t),改进模型与常规模型相同,无需进行冲击限制处理;当|âtarget(t)-atarget(t)-Δt|/Δt>ηjerk, max时,存在牵引/制动冲击,需按式(7)的等式形式计算atarget(t),可得由指令加速度acommand计算目标加速度atarget的冲击限制模型为
| ${a_{{\rm{turget }}}}(t) =\\ \left\{ {\begin{array}{*{20}{l}} {{a_{{\rm{command }}}}(t), 若\left| {{a_{{\rm{command }}}}(t) - {a_{{\rm{target }}}}(t - \Delta t)} \right|/\Delta t \le {\eta _{{\rm{jerk, max }}}};}\\ {{a_{{\rm{target }}}}(t - \Delta t) + \Delta t \cdot {\eta _{{\rm{jeth }}, {\rm{ max }}}}, 若\left[ {{a_{{\rm{conmand }}}}(t) - {a_{{\rm{target }}}}(t - \Delta t)} \right]/\Delta t > {\eta _{{\rm{jerk, max}}}};}\\ {{a_{{\rm{target }}}}(t - \Delta t) - \Delta t \cdot {\eta _{{\rm{jeth }}, {\rm{ max }}}}, 若\left[ {{a_{{\rm{target }}}}(t - \Delta t) - {a_{{\rm{command }}}}(t)} \right]/\Delta t > {\eta _{{\rm{jerk, max }}}}{\rm{. }}} \end{array}} \right. $ | (8) |
在地铁列车实际运行过程中,牵引/制动冲击通常发生在“阶跃式”指令加速度变化阶段,如列车在停车状态下收到一个较大牵引指令加速度时,或列车以较大制动减速度制动停车时.
2.2 牵引/制动响应模型在常规模型中,认为列车牵引/制动系统的实际响应加速度与目标加速度相同,没有考虑牵引/制动系统产生加速度的动态响应过程,无法准确反映列车的动态特性.在改进模型中,将列车的牵引/制动控制系统跟踪目标加速指令的过程近似为具有传输延迟的一阶系统,描述方程[18]为
| $\dot{a}_{\text {response }}(t)=-\frac{1}{T_{\mathrm{s}}} a_{\text {response }}(t)+\frac{K}{T_{\mathrm{s}}} a_{\text {target }}\left(t-T_{\mathrm{d}}\right). $ | (9) |
式中Ts、Td分别为牵引/制动控制系统的响应时间和传输延时,K为牵引/制动系统的响应特性系数.
为方便数值计算,将该模型改写为差分方程形式,牵引/制动系统的加速度响应模型可表示为
| $a_{\text {response }}(k)=b_{1} a_{\text {response }}(k-1)+b_{2} a_{\text {target }}(k-n-1). $ | (10) |
式中k表示控制周期号,n表示控制加速度传输延迟的周期数,b1、b2为模型参数.可根据列车目标加速度和响应加速度的测试数据,采用带有输入控制的自回归滑动平均模型(ARMAX),应用最小二乘法对加速度响应模型的模型参数b1、b2进行估计,并根据最小化代价函数准则来确定延迟周期数n.由于牵引系统和制动系统在特性方面的差异,列车在牵引工况下的牵引响应模型和制动工况下的制动响应模型的模型参数可能会略有不同.
考虑到地铁列车牵引/制动加速度响应过程的实际特点,在改进模型中用牵引/制动响应模型(10)代替常规模型(6)中的aresponse=atarget.综合上述分析,在改进模型中用aresponse代替acommand,代入式(3),响应加速度可表示为
| $a_{\text {response }}=a_{\text {train }}+d_{\text {basic }}+d_{\text {line }}. $ | (11) |
列车运行实测数据来源于哈尔滨地铁某线列车自动驾驶系统的测试数据,该路线正线开通段长4.6 km,包括5座地下车站,试车线长1.2 km,包括3个虚拟车站.运行测试时,在每一个站间运行区间,自动驾驶系统向列车输入指令加速度,并通过数据记录设备保存自动驾驶系统的相关计算数据、输出指令及当前列车运行状态信息.测试中对应的列车长119.32 m,动态质量为218.78 t,静态质量为208.88 t,基本阻力减速度经验公式(4)中的参数c0=4.97,c1=1.126×10-3、c2=6.636×10-5,重力加速度取9.81 m/s2,列车的冲击限制为0.75 m/s3.测试使用的线路坡道和曲线数据来自地铁公司技术文件,列车响应加速度测量值由实测的列车位置、速度和加速度数据根据式(11)获得.
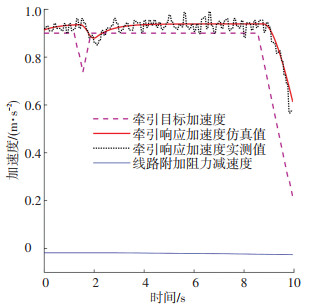
3.2 响应模型的验证及仿真分析由于列车牵引响应模型和制动响应模型具有相同的结构,图 1、图 2以牵引响应模型为例,验证2.2节所提出的响应模型的正确性,并证明该模型在提高速度仿真精度上的作用. 图 1中牵引目标加速度的最大冲击率为0.5 m/s3,满足列车冲击限制要求,有atarget=acommand,无需进行冲击限制处理,仅考察响应模型对速度计算精度的影响.该算例使用的测试数据为正线测试数据,根据列车位置计算得到线路附加阻力减速度如图 1所示.
|
图 1 牵引响应模型验证 |
|
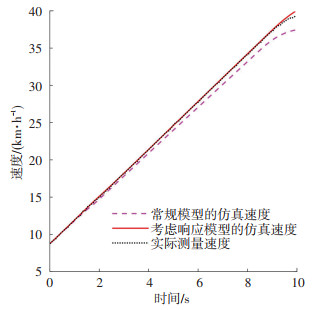
图 2 牵引响应模型对速度仿真的影响 Fig. 2 Influence of traction response model on speed simulation |
根据实测的牵引目标加速度和牵引响应加速度数据采用最小二乘法进行参数估计,得到牵引响应模型参数为:n=4,b1=0.927 3,b2=0.075 83. 图 1给出了牵引系统响应模型的目标加速度、响应加速度仿真值、响应加速度实测值曲线对比结果.从图中可以看出,牵引响应加速度的仿真值与实测值符合程度较高,表明该响应模型能较好地描述牵引系统的加速度响应过程. 图 2给出了对应图 1中的牵引目标加速度情况下,常规模型、考虑牵引响应的改进模型的速度仿真结果与实测速度的对比.随着计算时间的增加,仿真速度与实测速度之间的偏差会通过加速度偏差累积而逐渐增大,但考虑牵引响应的改进模型与实测速度之间的偏差要远小于常规模型产生的偏差.以图 2中的仿真结束时刻(t=10 s)为基准点,计算基于常规模型、响应模型的参考速度仿真结果与实际测量值的偏差,分别为-4.78%,1.63%,表明在常规模型基础上考虑响应模型可提高参考速度仿真精度.
3.3 改进模型对列车速度仿真的影响分析为分析冲击限制模型对速度仿真的影响,将制动指令加速度设置为“陡降式”,基于3.2节响应模型对参考速度影响的分析结果,通过修改冲击限制模型中列车最大冲击率的设置值,构造了两个改进模型.改进模型1和改进模型2均考虑响应模型,只在是否应用冲击限制模型上有所区别.在改进模型1中,令列车最大冲击率ηjerk, max=+∞,相当于不考虑冲击限制只考虑响应模型;在改进模型2中,令ηjerk, max=0.75 m/s3,相当于同时考虑冲击限制模型和响应模型.改进模型1和改进模型2采用同一组测试数据,包括“陡降式”指令加速度和响应加速度.本算例的测试数据为试车线测试数据,试车线为平直线路,线路附加阻力减速度为0.
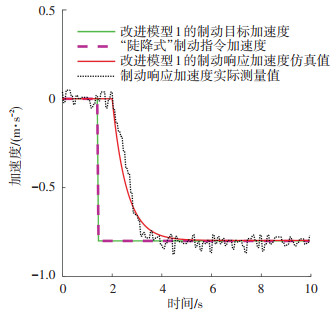
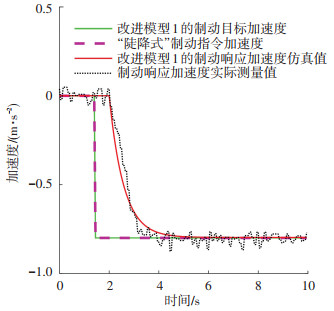
改进模型1和改进模型2的指令加速度、目标加速度、响应加速度仿真值和实测值分别如图 3、4所示.
|
图 3 改进模型1的制动响应模型 Fig. 3 Braking response model of improved model 1 |
|
图 4 改进模型2的制动响应模型 Fig. 4 Braking response model of improved model 2 |
在图 3中,由于改进模型1不考虑冲击限制,其目标加速度曲线与指令加速度曲线重合;在图 4中,改进模型2考虑了冲击限制模型,通过对指令加速度进行冲击限制处理生成缓变的目标加速度.根据目标加速度和制动响应加速度实测值,采用最小二乘法分别对改进模型1和改进模型2中的制动响应模型进行参数估计,得到改进模型1的制动响应模型参数n=11,b1=0.918,b2=0. 082;改进模型2的制动响应模型参数n=11,b1=0.529,b2=0.471.改进模型1和改进模型2的估计数据拟合度分别为90.92%、91.85%,最终预测误差分别为8.52×10-4、6.85×10-4,均方差分别为8.37×10-4、6.74×10-4,可见同时考虑冲击限制模型和响应模型的改进模型2比仅考虑响应模型的改进模型1有更高的加速度仿真精度.从图 3、4可以看出改进模型2考虑冲击限制模型得到的制动响应加速度计算值更接近实测值,说明对冲击限制模型的列车最大冲击率参数设定偏差会影响到列车响应模型的参数估计精度.
分别应用常规模型、改进模型1、改进模型2根据图 3、4中的“陡降式”指令加速度,对参考速度进行仿真计算,3种模型的计算结果与实测速度的对比如图 5所示.
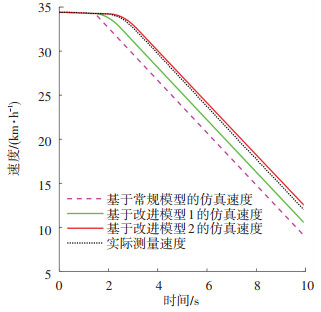
|
图 5 常规模型及改进模型仿真速度与实测速度的对比 Fig. 5 Comparison of measured speed and speed calculated by general model and the improved model |
以图 5中仿真结束时刻(t=10 s)为基准点,计算基于常规模型、改进模型1、改进模型2的仿真结果与实际速度测量值相比的参考速度仿真偏差,分别为-24.72%、-12.51%、4.00%.结果表明在常规模型基础上考虑响应模型提高参考速度仿真精度,在响应模型基础上考虑冲击限制模型可以进一步提高参考速度仿真精度.
4 结论1) 地铁列车运行参考速度计算的常规模型中将指令加速度等同于响应加速度,忽略了列车对指令加速度的冲击率约束过程和列车牵引制动系统对目标加速度的动态响应过程.改进模型在常规模型基础上,加入了由指令加速度生成目标加速度的冲击限制模型,和由目标加速度处理生成响应加速度的响应模型.
2) 响应模型符合列车加速度的实际变化规律,与常规模型相比,在牵引工况下和制动工况下,参考速度仿真精度可分别提高3.15%和12.21%.在响应模型基础上考虑冲击限制模型可进一步提高参考速度仿真精度,与仅考虑响应模型的情况相比,完整改进模型的参考速度计算精度可提高8.51%.改进模型的参考速度计算结果略高于实际测量值,在列车自动驾驶速度控制方面具有更好的安全性.
| [1] |
唐涛, 黄良骥. 列车自动驾驶系统控制算法综述[J]. 铁道学报, 2003, 25(2): 98. TANG Tao, HUANG Liangji. A survey of control algorithm for automatic train operation[J]. Journal of the China Railway Society, 2003, 25(2): 98. DOI:10.3321/j.issn:1001-8360.2003.02.021 |
| [2] |
荀径, 杨欣, 宁滨, 等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14. XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14. DOI:10.3969/j.issn.1001-8360.2014.04.003 |
| [3] |
丁勇. 列车运行计算与设计[M]. 北京: 北京交通大学出版社, 2011: 49. DING Yong. Train operation calculation and design[M]. Beijing: Beijing Jiaotong University Press, 2011: 49. |
| [4] |
饶忠. 列车牵引计算[M]. 北京: 中国铁道出版社, 2010: 24. RAO Zhong. Train traction calculation[M]. Beijing: China Railway Publishing House, 2010: 24. |
| [5] |
LIU R, GOLOVITCHER I. Energy-efficient operation of rail vehicles[J]. Transportation Research Part A: Policy and Practice, 2003, 37(10): 917. DOI:10.1016/j.tra.2003.07.001 |
| [6] |
LU S, HILLMANSEN S, HO T K, et al. Single-train trajectory optimization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 743. DOI:10.1109/TITS.2012.2234118 |
| [7] |
宿帅, 唐涛. 城市轨道交通ATO的节能优化研究[J]. 铁道学报, 2014, 36(12): 50. SU Shuai, TANG Tao. Optimal train control for ATO system[J]. Journal of the China Railway Society, 2014, 36(12): 50. DOI:10.3969/j.issn.1001-8360.2014.12.009 |
| [8] |
王青元, 冯晓云. 列车准点节能运行的控制工况最优切换研究[J]. 中国铁道科学, 2016, 37(2): 91. WANG Qingyuan, FENG Xiaoyun. Optimal switching for control conditions of punctual and energy efficient operation of train[J]. China Railway Science, 2016, 37(2): 91. DOI:10.3969/j.issn.1001-4632.2016.02.13 |
| [9] |
徐意. 城市轨道交通列车控制仿真模型研究[J]. 交通运输系统工程与信息, 2017, 17(5): 82. XU Yi. Modeling and simulation for trains control in urban rail transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(5): 82. DOI:10.16097/j.cnki.1009-6744.2017.05.012 |
| [10] |
石红国, 彭其渊, 郭寒英. 城市轨道交通牵引计算模型[J]. 交通运输工程学报, 2005, 5(4): 21. SHI Hongguo, PENG Qiyuan, GUO Hanying. Traction calculation model of urban mass transit[J]. Journal of Traffic and Transportation Engineering, 2005, 5(4): 21. |
| [11] |
朱晓敏, 徐振华. 基于单质点模型的城市轨道交通列车动力学仿真[J]. 铁道学报, 2011, 33(6): 14. ZHU Xiaomin, XU Zhenhua. Dynamic simulation of urban rail transit train based on single-particle model[J]. Journal of the China Railway Society, 2011, 33(6): 14. DOI:10.3969/j.issn.1001-8360.2011.06.003 |
| [12] |
唐金金, 周磊山, 佟路, 等. 单列高速列车运行仿真模型与算法[J]. 中国铁道科学, 2012, 33(3): 109. TANG Jinjin, ZHOU Leishan, TONG Lu, et al. Simulation model and algorithm for single high-speed train operation[J]. China Railway Science, 2012, 33(3): 109. DOI:10.3969/j.issn.1001-4632.2012.03.18 |
| [13] |
刘剑锋, 丁勇, 刘海冬, 等. 城市轨道交通多列车运行模拟系统研究[J]. 交通运输系统工程与信息, 2005, 5(1): 79. LIU Jianfeng, DING Yong, LIU Haidong, et al. Multi-train movement simulation system for urban rail transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2005, 5(1): 79. DOI:10.3969/j.issn.1009-6744.2005.01.015 |
| [14] |
林颖, 王长林. 车载ATO运行等级模式曲线的计算模型研究[J]. 铁道学报, 2013, 35(7): 50. LIN Ying, WANG Changlin. Computational model of operation level type profile of onboard ATO[J]. Journal of the China Railway Society, 2013, 35(7): 50. DOI:10.3969/j.issn.1001-8360.2013.07.008 |
| [15] |
地铁车辆通用技术条件: GB/T 7928—2003[S].北京: 中国标准出版社, 2004 General technical specification for metro vehicles: GB/T 7928—2003[S]. Beijing: China Standards Press, 2004 |
| [16] |
张安. 北京昌平线地铁车辆[J]. 机车电传动, 2011(3): 56. ZHANG An. Metro vehicle of Beijing Changping line[J]. Electric Drive for Locomotives, 2011(3): 56. DOI:10.13890/j.issn.1000-128x.2011.03.016 |
| [17] |
马沂文. 《地铁车辆通用技术条件》(GB/T 7928—2003)标准解读(待续)[J]. 电力机车与城轨车辆, 2005, 28(6): 64. MA Yiwen. Standard interpretation of general technical specification for metro vehicles (GB/T 7928—2003) (continued)[J]. Electric Locomotives & Mass Transit Vehicles, 2005, 28(6): 64. DOI:10.3969/j.issn.1672-1187.2005.06.023 |
| [18] |
于振宇, 陈德旺. 城轨列车制动模型及参数辨识[J]. 铁道学报, 2011, 33(10): 38. YU Zhenyu, CHEN Dewang. Modeling and system identification of the braking system of urban rail vehicles[J]. Journal of the China Railway Society, 2011, 33(10): 38. DOI:10.3969/j.issn.1001-8360.2011.10.007 |
 2019, Vol. 51
2019, Vol. 51


