作为近距离交通的有效方式,自行车交通是当前中国城市客运交通的重要组成部分,在城市客运出行结构中占有重要的地位.与此同时,随着城市化进程的加速及人民生活水平的不断提高,中国机动车保有量也呈现出几何增长趋势,机非互相影响是中国城市交通运行的主要特征之一.对于横断面形式为单幅路或两幅路的城市道路,机动车与路侧自行车仅通过标线分隔或混行,无疑对交通运行效率与安全造成不利影响,而如何量化及消除其影响还有待研究.
中国现行的《城市道路工程设计规范》[1]给出了一条自行车道的宽度为1 m,但并未就自行车道宽度的计算给出具体方法.在分析路侧自行车干扰对机动车交通的影响方面,文献[2]对比分析了信号交叉口的电动自行车对交通运行的安全影响.文献[3]分析了信号交叉口左转机非混合车流的离散特性,研究了其对左转机动车通行能力的影响.文献[4]对有无机非分隔设施条件下的驾驶人舒适性感知进行了研究.文献[5]构建了左转自行车对直行机动车通行的影响分析模型.文献[6]定量分析了自行车对机动车的摩擦干扰和阻滞干扰.文献[7]研究了无物理隔离路段的机动车与非机动车速度特征.文献[8]借鉴美国联邦公路局函数模型,构建了综合考虑机非干扰、对向干扰和横向干扰的路阻函数模型.文献[9]提出了一种考虑摩擦干扰的自行车与机动车混合交通流元胞自动机模型.文献[10]结合自行车元胞自动机改进模型和机动车改进模型,描述了存在摩擦干扰时车流的运行规律,分析了当自行车密度改变时机动车运行速度的变化.文献[11]通过对自行车流特性的研究和分析,研究了自行车流的微观、中观及广义元胞自动机建模.文献[12]研究了机非划线分隔道路的自行车交通流对机动车运行的影响.文献[13]分析给出了信号交叉口机非隔离设施的设置条件.
综上所述,已有的相关研究对如何减轻机非冲突考虑较少,而中国许多城市的自行车出行比例较高,且很多道路仅是采用划线分隔机动车与非机动车,存在机非冲突隐患.本文拟基于机非冲突次数与自行车数量关系分析,研究给出能够保证机非冲突不达到严重等级的自行车道宽度计算方法,从而为城市道路交通规划、设计与管理部门提供依据与参考.值得指出的是,《城市道路工程设计规范》[1]中给出的一条自车行道宽度为1 m,其依据为“自行车车身宽度0.6 m和根据《中华人民共和国道路交通安全法实施条例》规定的载物宽度,左右都不得超出车把0.15 m,并考虑行驶时的左右摆幅宽度”,本文即依据《城市道路工程设计规范》[1]中给出的一条自行车道宽度,基于机非冲突分析研究自行车道总宽度的计算方法.而电动自行车的车身宽度明显大于普通自行车的0.6 m,对于有电动自行车通行的一条自行车道宽度,现行规范中尚未有规定,因此,本文的研究对象不包括电动自行车,研究成果适用于不允许电动自行车使用的自行车道.
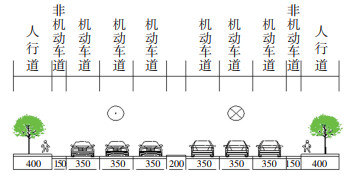
1 数据调查与分析 1.1 调查地点与调查内容本次调查选取河北省廊坊市的主、次干路及支路各1条,主干路为光明西道(廊坊一中附近),路段长520 m,设计速度为50 km/h,双向6车道,机动车道宽21 m,两幅路断面;次干路路段为丰盛路(建华里小区附近),长450 m,设计速度为40 km/h,双向4车道,机动车道宽度14 m,单幅路断面;支路路段为建设路(廊坊三中附近),长310 m,设计速度30 km/h,双向2车道,机动车道宽度7.0 m,单幅路断面. 3条调查路段均采用标线分隔机动车与自行车,无物理隔离设施.调查地点均存在路侧自行车干扰(本文的调查路段基本无电动自行车,故未考虑电动自行车,在统计数据时也未计入其交通量),自行车道宽1.5 m,即一条自行车道.调查路段的横断面布置具体见图 1~3,百度地图实景及相邻路网见图 4~9.
|
图 1 主干路横断面布置 Fig. 1 Cross-sectional layout of arterial road |
|
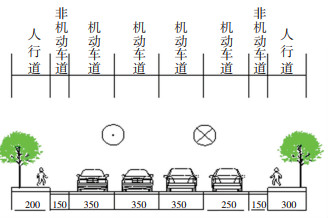
图 2 次干路横断面布置 Fig. 2 Cross-sectional layout of sub-arterial road |

|
图 3 支路横断面布置 Fig. 3 Cross-sectional layout of branch road |

|
图 4 光明西道百度实景图 Fig. 4 Baidu view map of Guangming West Road |
|
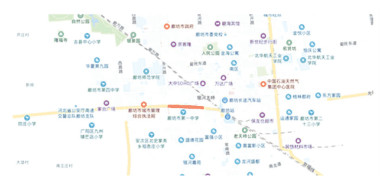
图 5 光明西道相邻路网 Fig. 5 Adjacent road network of Guangming West Road |

|
图 6 丰盛路百度实景图 Fig. 6 Baidu view map of FengshengRoad |
|
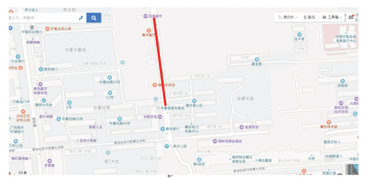
图 7 丰盛相邻路网 Fig. 7 Adjacent road network of Fengsheng road |

|
图 8 建设路百度实景图 Fig. 8 Baidu view map of Jianshe Road |
|
图 9 建设路相邻路网 Fig. 9 Adjacent road network of Jianshe Road |
调查时间为2018年4月25日(星期三)上午高峰期7:30—8:00,每组数据的调查时段按1 min计.需要获取的数据包括:路侧自行车数量、机非冲突次数.目前,关于交通冲突能够被广泛接受的定义是:在道路上,两个及两个以上交通参与者在运行或静止过程中,如果双方感知到危险的存在,若不采取任何措施则必然会有事故产生,而一旦采取措施即能完全避免事故发生,这种从交通参与者感知到危险存在持续到事故被有效制止的过程称为交通冲突.本文认为机非冲突过程中驾驶人与骑行者所采取的措施包括制动和改变行驶轨迹,在对视频数据提取的过程中,判定机动车与自行车之间产生冲突的依据即为当二者接近时驾驶人或骑行者采取了制动或转向操作.本文所研究的机非冲突主要是指机动车或自行车压线或跨线侵入对方行使空间(自行车道或机动车道).此外,本文研究的主要目的是基于机非冲突数量与单车道自行车数量的关系建模,计算不发生严重冲突所需要的自行车道宽度,在整个研究过程中并不需要自行车速度数据,故现场观测并未调查自行车速度数据.
需要注意的是,必须保证数据的同步性,即自行车数量与机非冲突次数同时观测.采用视频观测法,在路段适当位置架设摄像机,对最外侧机动车流和自行车进行摄像记录.自行车数量与机非冲突次数可由视频资料查取,在对视频数据处理过程中若发现提取数据异常会直接纠正,故处理得到的数据中并无异常数据点.提取的视频数据见表 1,调查样本总计90组.
| 表 1 路侧自行车数量与机非冲突次数数据 Tab. 1 Data of the number of roadside bicycle and the number of conflict between automobile and bicycle |
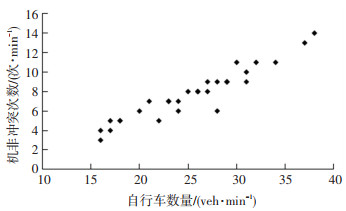
表 1中,路侧自行车数量为1 min内1条自行车车道的数值,机非冲突次数为1 min内自行车与邻近车道(与自行车道邻近的车道,即最外侧车道)机动车的冲突数量数据.根据表 1中的数据,得到主、次干路及支路机非冲突次数与路侧自行车数量的散点图,如图 10~12所示.
|
图 10 主干路机非冲突次数与路侧自行车数量散点图 Fig. 10 Scatter points of the number of conflict on arterial road and the number of roadside bicycle |
|
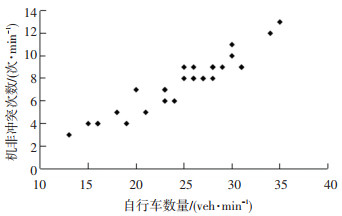
图 11 次干路机非冲突次数与路侧自行车数量散点图 Fig. 11 Scatter points of the number of conflict on sub-arterial road and the number of roadside bicycle |
|
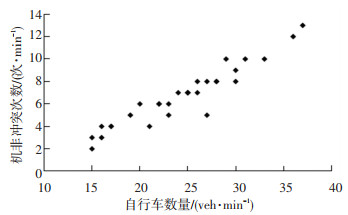
图 12 支路机非冲突次数与路侧自行车数量散点图 Fig. 12 Scatter points of the number of conflict on branch road and the number of roadside bicycle |
从图中可以看出,随着路侧自行车数量的增加,邻近车道的机非冲突次数逐渐增大.根据本此调查采集到的视频,发现外侧车道机动车受干扰的因素包括两种情况:一是自行车进入机动车道行驶,产生机非冲突;二是自行车虽未驶入机动车道,但由于压线行驶或距离机非分隔标线过近,造成机动车横向净距不足,从而导致机非冲突.
2 机非冲突次数与自行车数量关系模型 2.1 主干路对图 4的散点分别进行可能的函数关系拟合,得到主干路路侧自行车数量与机非冲突次数的可能关系函数式,见表 2.
| 表 2 主干路机非冲突次数与自行车数量拟合函数 Tab. 2 Fitting functions of the number of conflict on arterial road and the number of roadside bicycle |
由表 2及其相关参数可知,对于主干路路侧自行车数量与机非冲突次数关系的拟合,二次函数拟合程度更高,因此采用幂函数表示为
| $N_{1}=0.004\;9 q_{\mathrm{B} 1}^{2}+0.166\;3 q_{\mathrm{B} 1}+0.163\;5. $ | (1) |
式中:N1为主干路机非冲突次数,次/min;qB1为主干路路侧单车道自行车数量,veh/min.
2.2 次干路对图 5的散点分别进行可能的函数关系拟合,得到次干路路侧自行车数量与机非冲突次数的可能关系函数式,见表 3.
| 表 3 次干路机非冲突次数与自行车数量拟合函数 Tab. 3 Fitting functions of the number of conflict on sub-arterial road and the number of roadside bicycle |
由表 3及其相关参数可知,对于次干路路侧自行车数量与机非冲突次数关系的拟合,幂函数拟合程度更高,因此采用幂函数表示为
| $N_{2}=0.082\;6 q_{\mathrm{B} 2}^{1.4017}. $ | (2) |
式中:N2为次干路机非冲突次数,次/min;qB2为次干路路侧单车道自行车数量,veh/min.
2.3 支路对图 6的散点分别进行可能的函数关系拟合,得到支路路侧自行车数量与机非冲突次数的可能关系函数式,见表 4.
| 表 4 支路机非冲突次数与自行车数量拟合函数 Tab. 4 Fitting functions of the number of conflict on branch road and the number of roadside bicycle |
由表 4及其相关参数可知,对于支路路侧自行车数量与机非冲突次数关系的拟合,二次函数拟合程度更高,因此采用二次函数表示为
| $N_{3}=0.004\;9 q_{\mathrm{B} 3}^{2}+0.176\;1 q_{\mathrm{B} 3}-0.665\;3 $ | (3) |
式中:N3为支路机非冲突次数,次/min;qB3为支路路侧单车道自行车数量,veh/min.
3 机非冲突分级与自行车道宽度计算 3.1 基于事故预测的机非冲突分级文献[14]研究得到交通冲突转化为交通事故的概率为0.000 1,本文取该值作为本文的机非事故发生概率.根据式(1)~(3),可以得到城市主、次干路和支路机非事故日发生数量(12 h)的预测模型分别为
| $A_{1}=0.000\;35 q_{\mathrm{B} 1}^{2}+0.011\;97 q_{\mathrm{B} 1}+0.011\;77, $ | (4) |
| $A_{2}=0.005\;9 q_{B 2}^{1.401\;7}, $ | (5) |
| $A_{3}=0.000\;35 q_{\mathrm{B} 3}^{2}+0.012\;671 q_{\mathrm{B} 3}-0.047\;9. $ | (6) |
式中:A1为主干路日机非事故预测数量,次/d;A2为次干路日机非事故预测数量,次/d;A3为支路日机非事故预测数量,次/d.
根据式(4)~(6),可推导出主、次干路和支路对应不同机非事故日发生数量的路侧单车道自行车数量计算公式分别为
| $q_{\mathrm{B} 1}=-17.1+\sqrt{258.8+2857.1 A_{1}}, $ | (7) |
| $q_{\mathrm{B} 2}=\left(169.5 A_{2}\right)^{0.713}, $ | (8) |
| $q_{\mathrm{B} 3}=-18.1+\sqrt{464.5+2\;857.1 A_{3}}. $ | (9) |
随着机非冲突次数的增多,会导致机非事故发生,本文取机非事故平均每周发生一次对应的机非冲突为严重冲突[14],即每天发生机非事故的数量为1/7次,在式(7)~(9)中,将1/7次分别代入A1、A2、A3,分别得到
| $\begin{aligned} q_{\mathrm{B} 1} &=524 \text { veh}/(\mathrm{h} \cdot \ln ), \\ q_{\mathrm{B} 2} &=582\;\mathrm{veh} /(\mathrm{h} \cdot \ln ) , \\ q_{\mathrm{B} 3} &=686 \mathrm{veh} /(\mathrm{h} \cdot \ln ). \end{aligned} $ |
取机非事故平均每月发生一次对应的机非冲突为一般冲突[14],即每天发生机非事故的数量为1/30次,在式(7)~(9)中,将A1、A2、A3分别代入1/30次,分别得到
| ${q_{{\rm{B}}1}} = 103{\rm{\;veh}}/({\rm{h}} \cdot \ln ), $ |
| $q_{\mathrm{B} 2}=206 {\rm{\;veh}}/(\mathrm{h} \cdot \ln ), $ |
| $q_{\mathrm{B} 3}=334{\rm{\;veh}}/ (\mathrm{h} \cdot \ln ). $ |
综上计算,城市干路机非冲突分级见表 5,当城市主、次干路和支路的路侧非机动车数量分别达到或超过524、582、686 veh/(h·ln)时,本文认为其产生的机非冲突较为严重,此时需拓宽自行车道,增加自行车道数量;或增设物理分隔设施,避免机非冲突.
| 表 5 基于路侧自行车数量的机非冲突等级划分 Tab. 5 Conflict grade between automobile and bicycle based on the number of roadside bicycle |
从表 5中可以看出,随着道路等级的降低,各级机非冲突对应的自行车数量阈值随之变大,分析其原因,是由于主干路的车速要高于次干路和支路,次干路要高于支路,车速高会导致在相同的自行车数量条件下其冲突数量增加;反之,在相同的机非冲突次数条件下,其对应的自行车交通量变小.因此,呈现出划分机非冲突等级的自行车数量阈值随道路等级降低而变大的规律.
3.2 自行车道宽度计算《城市道路工程设计规范》[1]规定:受平面交叉口影响的一条自行车道的路段设计通行能力,当无分隔时,应取800~1 000 veh/h.显然本文提出的自行车数量阈值要低于规范值,规范值是从通行效率角度给出的,而本文则是从行车安全角度出发,对于保障自行车骑行者的安全具有现实意义.按照规范中的一条自行车道宽度为1 m计算,可以得到主、次干路和支路自行车道宽度的计算公式分别为
| $W_{\mathrm{B} 1}=\operatorname{INT}\left(\frac{Q_{\mathrm{B} 1}}{524}\right)+1, $ | (10) |
| $W_{\mathrm{B} 2}=\mathrm{INT}\left(\frac{Q_{\mathrm{B} 2}}{582}\right)+1, $ | (11) |
| $W_{\mathrm{B} 3}=\mathrm{INT}\left(\frac{Q_{\mathrm{B} 3}}{686}\right)+1. $ | (12) |
式中:INT代表对数字进行取整规则;WB1为主干路自行车道宽度,m;QB1为主干路路侧自行车数量,veh/h;WB2为主干路自行车道宽度,m;QB2为次干路路侧自行车数量,veh/h;WB3为支路自行车道宽度,m;QB3为支路路侧自行车数量,veh/h.
3.3 实例分析对本文调查的路段进行分析,发现现有自行车道宽度均不足,机非冲突严重,需对其进行拓宽.根据式(10)~(12),可计算得到调查路段自行车道拓宽宽度值,见表 6.从表中可以看出,各条路段在拓宽自行车道后,其机非冲突次数会明显减少,从而保证自行车安全.若要保证所有时段均不出现严重冲突,自行车道宽度应取表 6中的最大值,即主干路取5 m,次干路和支路取4 m;但考虑拓宽值过大具有实施难度,故建议主、次干路与支路路段自行车道宽度优化值分别取4、3、3 m(出现频率较高).
| 表 6 调查路段自行车道拓宽宽度计算值 Tab. 6 Width of bicycle lane of observed road sections |
值得指出的是,在红线宽度受限无法对自行车道进行拓宽时(尤其是所需自行车道宽度较宽,见表 5中的4 m和5 m),可采取机非物理分隔(如设置机非隔离栅栏)方式避免机非冲突.拓宽车道与设置机非物理分隔设施均可作为管理者的决策备选方案.
4 结论1) 对于单幅路与两幅路断面的城市主、次干路,路侧自行车数量对机非冲突次数均有影响,路侧自行车数量与机非冲突次数呈正相关,主干路和支路的关系函数均为递增的二次函数,次干路关系函数为递增的幂函数.
2) 基于构建的路侧自行车数量与机非冲突次数关系模型,以及交通冲突次数与事故数量的关系,给出了基于路侧自行车数量的机非冲突严重等级划分标准,以不达到严重冲突为目标,给出了自行车道宽度计算方法.
3) 实例分析表明,应用基于城市道路机非冲突分析的自行车道宽度计算方法,对现有的自行车道进行拓宽或合理规划新建的自行车道宽度,可以较为显著地降低机非冲突次数,保障自行车行车安全.
4) 以机动车与自行车无物理隔离设施情况展开研究,而当有物理隔离的情况下,自行车与机动车不会产生交通冲突,此时,自行车道宽度可参照《城市道路工程设计规范》中的通行能力规定(受平面交叉口影响的一条自行车道的路段设计通行能力,当有机非分隔设施时,应取1 000~1 200 veh/h)计算选取.同时,鉴于中国电动自行车保有量较大,关于电动自行车通行的自行车道宽度,将作为下一步的研究重点.
| [1] |
中华人民共和国住房和城乡建设部.城市道路工程设计规范: CJJ37—2012 [S].北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of urban road engineering: CJJ37—2012 [S]. Beijing: China Architecture & Building Press, 2012 |
| [2] |
BAI L, LIU P, CHEN Y, et al. Comparative analysis of the safety effects of electric bikes at signalized intersections[J]. Transportation Research Part D, 2013, 20(5): 48. |
| [3] |
CHEN J X, WANG W, LI Z B, et al. Dispersion effect in left-turn mixed bicycle traffic and its influence on capacity of left-turn vehicles at signalized intersections[J]. Transportation Research Record, 2014, 2468: 38. DOI:10.3141/2468-05 |
| [4] |
LI Z, WANG W, LIU P, et al. Physical environments influencing bicyclists' perception of comfort on separated and on-street bicycle facilities[J]. Transportation Research Part D, 2012, 17(3): 256. DOI:10.1016/j.trd.2011.12.001 |
| [5] |
徐良杰, 王炜. 左转自行车对直行机动车通行的影响分析模型[J]. 东南大学学报(自然科学版), 2005, 35(5): 805. XU Liangjie, WANG Wei. Analysis model of influence of left-turn bicycle on passage of straight-through vehicles[J]. Journal of Southeast University, 2005, 35(5): 805. DOI:10.3321/j.issn:1001-0505.2005.05.032 |
| [6] |
贾顺平, 彭宏勤, 郭谨一, 等. 城市混合交通中自行车对机动车行驶影响的定量分析[J]. 交通运输系统工程与信息, 2008, 8(2): 58. JIA Shunping, PENG Hongqin, GUO Jinyi, et al. Quantitative analysis of impact of bicycles on vehicles in urban mixed traffic[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(2): 58. DOI:10.3969/j.issn.1009-6744.2008.02.009 |
| [7] |
陈永恒, 王殿海, 陶志兴. 无物理隔离路段机动车与非机动车速度特性研究[J]. 交通运输系统工程与信息, 2009, 9(5): 53. CHEN Yongheng, WANG Dianhai, TAO Zhixing. Speed character study for motor vehicle and bicycle at non-barrier section[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(5): 53. DOI:10.3969/j.issn.1009-6744.2009.05.009 |
| [8] |
任刚, 刘晓庆. 混合交通条件下的城市道路实用路阻函数[J]. 中国公路学报, 2009, 22(4): 92. REN Gang, LIU Xiaoqing. Practical link performance functions for urban roads with mixed traffic[J]. China Journal of Highway and Transport, 2009, 22(4): 92. DOI:10.3321/j.issn:1001-7372.2009.04.015 |
| [9] |
贾宁, 马寿峰. 考虑摩擦干扰的机非混合交通流元胞自动机仿真[J]. 系统仿真学报, 2011, 23(2): 390. JIA Ning, MA Shoufeng. Simulation of mixed traffic flow with friction interference using cellular automata[J]. Journal of System Simulation, 2011, 23(2): 390. |
| [10] |
应力天.基元胞自动机的城市路段混合交通流建模与仿真[D].北京: 北京交通大学, 2008 YING Litian. Models and simulations on mixed traffic in urban section road based on the theory of cellular automaton[D]. Beijing: Beijing Jiaotong University, 2008 |
| [11] |
张兰渝.混合交通流下自行车流的混杂建模及研究[D].杭州: 浙江大学, 2011 ZHANG Lanyu. Studies on hybrid modeling of bicycle flow based on mixed traffic flow[D]. Hangzhou: Zhejiang University, 2011 |
| [12] |
林贵宝, 马荣国, 杨泞珲. 机非划线分割道路自行车交通流对机动车运行的影响[J]. 公路交通科技, 2016, 33(1): 112. LIN Guibao, MA Rongguo, YANG Ninghui. Impact of bicycle traffic on vehicle operation on divided road[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 112. DOI:10.3969/j.issn.1002-0268.2016.01.017 |
| [13] |
徐闯闯.信号交叉口机非隔离设施设置条件分析[D].南京: 东南大学, 2015 XU Chuangchuang. Analysis of barrier facilities setting conditions at signalized intersections[D]. Nanjing: Southeast University, 2011 |
| [14] |
成卫.城市道路交通事故与交通冲突技术理论模型及方法研究[D].长春: 吉林大学, 2004 CHENG Wei. Theoretical model and method of urban road traffic accident and conflict technique[D]. Changchun: Jilin University, 2004 |
 2019, Vol. 51
2019, Vol. 51


