2. 东南大学 交通学院,南京 210096
2. School of Transportation, Southeast University, Nanjing 210096, China
沥青混合料是一种典型的温度敏感性材料,随温度的不同,沥青混合料呈现出3种明显不同的流变学状态:玻璃态、橡胶态、粘流态.玻璃态转变温度是材料在温度变化过程中的一个临界温度,在该温度之前材料处于玻璃态,表现为模量较高的脆性体.当温度继续升高到一定范围后,材料表现为柔软而富有弹性的橡胶态.通常将玻璃态与橡胶态之间的转变区域称为玻璃态转变,所对应的转变温度定义为玻璃态转变温度.在该转变温度处,材料的物理、化学性能发生骤变,因此材料的玻璃态转变温度具有丰富的工程意义[1].
材料的玻璃态转变温度与材料的低温性能密切相关,文献[2-4]通过试验证明玻璃态转变温度与沥青混合料的低温性能密切相关.当材料处于玻璃态时,材料的分子锻链结构几乎处于冻结状态,因此材料在较小的形变便可能被破坏.而当材料的温度高于其玻璃态转变温度时,由于分子锻链开始解冻,分子运动空间变大,材料拥有较好的变形能力.
材料的玻璃态转变温度可以通过试验直接测量,测量原理主要是利用材料在玻璃态转变温度时,力学性质和物理性质发生显著变化或突变.原则上说,所有在该时刻发生显著变化和突变的物理性质,都可以用来测量材料的玻璃态转变温度[5].例如材料的体积、膨胀系数、比热容、介电常数等.
材料的玻璃态转变温度是高分子锻链运动从冻结到运动(或与之相反)的一个转变温度,因此凡是能够影响分子链柔韧性的因素都可以对玻璃态转变温度产生影响[6].而沥青混合料作为一种多相粘弹性材料,其各项性能指标和力学响应具有明显的温度、荷载依赖性,在不同气候、荷载和行车速度等条件的耦合下,材料将产生不同的粘弹响应.
综上所述,目前对于材料玻璃态转变温度的研究主要集中于探讨材料玻璃态转变温度与低温性能的相关性以及材料玻璃态转变温度的确定方法.鉴于此,本研究选取升温速率、荷载频率、应变水平3个因素模拟沥青混合料在不同气候、不同交通量下的服役行为,利用动态力学分析仪测定沥青混合料在不同条件下的玻璃态转变温度,通过对试验结果的统计分析,确定影响沥青混合料玻璃态转变温度的主要因素,并且建立多因素综合作用下沥青混合料玻璃态转变温度的预估模型.
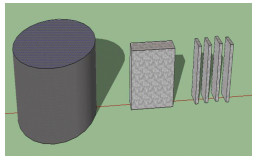
1 玻璃态转变温度影响因素分析 1.1 试验设计 1.1.1 试验材料与试件切割本试验采用的沥青混合料切片长为(60±5)mm,宽为(15±1)mm,厚为(3±0.1)mm.沥青混合料切片试件的切割分两步进行,首先将SGC压实成型的试件用切割机切割为长45 mm,宽45 mm,高10 mm的长方体试块,再用高精度切割机(切割精度10 μm)将试块切割为规定尺寸的切片试件,切割过程如图 1所示.由于试验所需沥青混合料尺寸较小,如果混合料级配较粗,可能导致试验结果变异性增大,为增加试验结果精度,本试验采用细粒式沥青混合料AC-5,矿料关键筛孔(4.75、2.36、0.075 mm)的通过率分别为100%、84.8%、10%,沥青胶浆为SBS改性沥青,沥青混合料油石比为6.5%.
|
图 1 试件切割过程示意图 Fig. 1 Procedure ofsample shaping |
沥青混合料玻璃态转变温度试验使用DMA(Q800)动态力学分析仪对沥青混合料进行温度扫描试验.即对沥青混合料试件在某一加载频率下施加恒定应变和线性加热速率,按照0.01 s的时间间隔采集沥青混合料在升温过程的粘弹参数.试验时首先将沥青混合料切片试件固定在DMA双悬臂夹具上,如图 2(a)所示,然后在弯拉受力模式下对试件进行温度扫描,如图 2(b)所示.试验采用氮气控制工作炉内的环境温度,对试件进行温度扫描时工作炉内的热电偶实时测量和采集试件温度.

|
图 2 DMA设备简介图 Fig. 2 Schematic of DMAequipment |
试验设计采用控制变量法分别探究升温速率、荷载频率、应变水平对沥青混合料玻璃态转变温度的影响.温度扫描作为材料流变特性分析的一种方法,在试验过程中材料需处于线粘弹性区域,因此在温度扫描试验前需进行应变扫描确定材料的线粘弹性区域(liner viscoelastic region, LVR).根据相关研究表明,如果沥青混合料的复数模量降低至不超过其最大复数模量的10%,则沥青混合料处于线粘弹性区间内.文献[7]发现沥青的线粘弹性区间随着温度的降低而减小;文献[8]研究发现沥青的线粘弹性区间随着频率的降低而减小.考虑到本研究试验条件组合方式较多,选择线粘弹性区间最小的情况进行应变扫描,即在温度-20 ℃、0.1 Hz的条件下利用DMA对沥青混合料切片进行应变扫描试验.通过试验得到当应变水平小于0.02%时沥青混合料处于线粘弹性区间.根据应变扫描的结果确定温度扫描试验方案如下:1)升温速率对材料玻璃态转变温度影响试验.温度过程为首先在初始温度-20 ℃恒温10 min,然后分别按照0.2、0.5、1、2、4、8 ℃/min的升温速率至80 ℃,试验的应变水平为0.003%,加载频率为10 Hz.每个升温速率下进行3次平行试验. 2)荷载频率对材料玻璃态转变温度影响试验.温度过程为首先在初始温度-20 ℃恒温10 min,然后以1 ℃/min升温速率上升至80 ℃,试验的应变水平为0.003%,试验的加载频率分别为0.1、1、10、25、50、80 Hz.每个荷载频率下进行3次平行试验. 3)应变水平对材料玻璃态转变温度影响试验.温度过程为首先在初始温度-20 ℃恒温10 min,然后以1 ℃ /min升温速率上升至80 ℃,荷载频率为10 Hz.试验的应变水平分别为0.003、0.006、0.009、0.012、0.015、0.018%.每个应变水平下进行3次平行试验.
1.2 试验数据处理与分析 1.2.1 玻璃态转变温度的确定文献[9]提出利用材料在动态力学试验中的粘弹参数的变化曲线来确定材料的玻璃态转变温度;文献[10]根据材料的动态力学性能谱提出了3种玻璃态转变温度的定义方法:1)将储能模量曲线上折点所对应的温度定义为Tg;2)将损耗模量的峰值点所对应的温度定义为Tg;3)将相位角的峰值定义所对应的温度为Tg. 3种不同的定义方法如图 3所示.

|
图 3 玻璃态转变温度定义 Fig. 3 Definition of glass transition temperature |
不同的研究采用的玻璃态转变温度的定义方法不同,本研究将复数模量E-T曲线折点所对应的温度定义为沥青混合料的玻璃态转变温度.为更加准确地获取材料的玻璃态转变温度,本研究采用Boltzmann模型对E-T曲线进行拟合,该模型函数表达式为
| $y=\frac{A_{1}-A_{2}}{1+\mathrm{e}^{\left(x-x_{0}\right) / \mathrm{d} x}}+A_{2}. $ | (1) |
式中:y为材料模量的对数值,x为温度值,A1、A2、dx、x0均为回归系数,x0为曲线拐点;y=A1、y=A2为Boltzmann函数的上下两条渐近线.
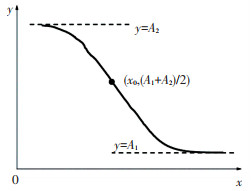
曲线特征如图 4所示,曲线折点横坐标即材料的玻璃态转变温度Tg, 计算公式为
|
图 4 Boltzmann函数 Fig. 4 Boltzmann function |
| $T_{g}=-2 \mathrm{d} x+x_{0}. $ | (2) |
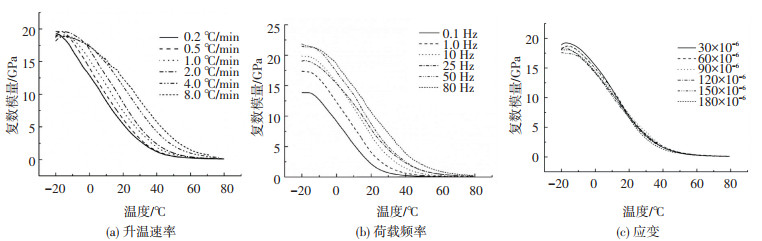
按照试验方案对沥青混合料试件进行不同升温速率、不同荷载频率以及不同应变水平下的温度扫描试验,得到图 5所示的温度谱. 图 5(a)描述了材料在不同升温速率下复数模量变化规律.由图可知:在低温和高温区,不同升温速率的E-T曲线较为接近,即在该区段内沥青混合料的复数模量水平接近.而在中温区,升温速率越高,曲线在水平方向上越偏向右侧. 图 5(b)描述了不同荷载频率下复数模量变化规律.由图可见,在中温与低温区,荷载频率越高,沥青混合料的初始复数模量越大,E-T曲线的位置越高,而随着温度的升高,不同频率的下材料的复数模量的差距逐渐缩小.图 5(c)反应了不同应变水平下复数模量E-T曲线的变化规律.由图可见,不同应变水平下材料的E-T曲线无明显变化,曲线特征几乎保持一致.
|
图 5 不同控制因素下沥青混合料温度谱 Fig. 5 Temperature spectrum of asphalt mixture under different control factors |
为明确材料的玻璃态转变温度在各试验因素下的变化规律,采用Boltzmann模型拟合上图中的温度谱曲线,并计算得到沥青混合料在不同升温速率、不同荷载频率以及不同应变水平下的玻璃态转变温度,对结果进行单因素方差分析.结果分别见表 1~6.
| 表 1 不同升温速率下沥青混合料Tg试验结果表 Tab. 1 Tg of asphalt mixture under different heating rates |
| 表 2 不同升温速率下沥青混合料Tg方差分析表 Tab. 2 ANOVA of Tg under different heating rates |
| 表 3 不同荷载频率下沥青混合料Tg试验结果表 Tab. 3 Tg of asphalt mixture under different load frequencies |
| 表 4 不同升温速率下沥青混合料Tg方差分析表 Tab. 4 ANOVA of Tg under different heating rates |
| 表 5 不同应变水平下沥青混合料Tg试验结果表 Tab. 5 Tg of asphalt mixture under different strain levels |
| 表 6 不同应变水平下沥青混合料Tg方差分析表 Tab. 6 ANOVA of Tg under different strain levels |
综合表 1~6可知,同一试验水平下不同试验样本的玻璃态转变温度的变异系数均小于15%,表明Boltzmann模型拟合结果稳定.沥青混合料的玻璃态转变随着升温速率的增加而逐渐升高.且由于F0.01(5, 12)=3.11 < 284.41,故在0.01的显著性水平下可以认为升温速率对于材料的玻璃态温度有显著影响;沥青混合料的玻璃态转变温度随着荷载频率的增大而升高.且F0.01=3.11 < 19.69,故在显著性水平0.01下可以认为荷载频率对于材料的玻璃态温度有着显著影响;不同应变水平下的玻璃态转变温度无明显变化规律,只是在某一温度左右浮动.由于F0.01(5, 12)=3.11>1.89,故在0.01显著性水平下,不同应变水平下材料的玻璃态转变温度变化较小,由此表明:在线粘弹性区域内,沥青混合料的玻璃态转变温度并无明显的应变依赖性.
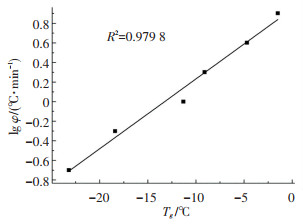
通过上述分析发现升温速率与荷载频率对沥青混合料的玻璃态转变温度有显著影响,为明确上述指标与玻璃态转变温度的关系,分别以试验的升温速率的对数值lg φ、荷载频率的对数值lg f为纵坐标、材料的玻璃态转变温度Tg为横坐标,得到如图 6、7所示的关系.
|
图 6 玻璃态转变温度与升温速率关系 Fig. 6 Relationship between Tg and hating rate |

|
图 7 玻璃态转变温度与荷载频率关系 Fig. 7 Relationship between Tg and load frequency |
由图 6可知,沥青混合料的玻璃态转变温度与升温速率对数值存在良好的线性相关性:lg φ=0.071 6 Tg+0.949 2,线性相关系数大于0.95.按照自由体积的概念,在玻璃态转变温度以上,分子通过锻链运动腾出多余的自由体积,因此在升温过程中,自由体积逐渐增大,但是由于温度升高导致锻链之间的阻力减小,这种位置调整不能及时跟进,致使沥青的体积总比该温度下最后应该具有的平衡体积小,升温速率越大,位置调整的滞后性越明显,进而导致沥青混合料的玻璃态转变温度越高.
由图 7可见,沥青混合料的玻璃态转变温度与荷载频率的对数值之间存在良好的线性相关性:lg f=-0.388 5Tg+4.516 7,两者线性相关系数大于0.95,因此荷载频率能够明显的影响材料的玻璃态转变温度.主要原因是测试频率的变化相当于沥青混合料内部自由体积分数的变化,较短的测试周期(较高的测试频率)相当于较大的自由体积分数,而较长的测试周期(较低的测试频率)相当于较小的自由体积分数.因此沥青混合料的玻璃态转变温度随着频率的增高而升高.
为确定试验因素各水平间的差异性,采用“S检验”法对设计试验水平进行事后多重比较[11].首先列出因素各水平下指标平均值的差数三角形,差数三角形的第1列按照指标平均值由大到小的顺序从上到下排列,第1行按照指标平均值由小到大从左到右排列,y(i)表示指标均值按照从大到小的第i个排列,Ai为y(i)所对应的水平.在给定的检验水平α下,计算
| 表 7 升温速率各试验水平差异性 Tab. 7 Comparison of test results under different heating rates |
| 表 8 荷载频率各试验水平差异性 Tab. 8 Comparison of test results under different load frequencies |
除个别试验水平下的玻璃态转变温度无显著性差异外,其余各水平下的试验结果均存在明显的差异性,表明了沥青混合料在不同荷载频率、不同升温速率下具有迥异的粘弹特性响应,也证明了沥青混合料是一种温度(频率)敏感性材料.沥青路面服役条件受地域气候、材料特性及结构层位等因素影响,呈现出较大的波动性,因此开展不同升温速率、不同频率下的沥青混合料的玻璃态转变温度试验,有助于掌握沥青混合料在不同服役条件下的玻璃态转变特性.
2 玻璃态转变温度多因素预测模型 2.1 全因素试验设计在沥青混合料玻璃态转变温度影响因素分析中,通过试验发现升温速率、荷载频率对材料的玻璃态转变温度有明显的影响,在线粘弹性区域内沥青混合料的玻璃态转变温度无明显的应变依赖性.为进一步探讨沥青混合料玻璃态转变温度在多因素影响下的变化规律,建立多因素下的沥青混合料玻璃态转变温度预测模型,本节试验选择升温速率A(共6个试验水平:0.2、0.5、1、2、4、8 ℃/min)、荷载频率B(共6个试验水平:0.1、1、10、25、50、80 Hz)两个试验因素进行全因素试验设计.试验材料和试验设备与前述试验相同,每个试验水平需进行3次重复试验以提高试验结果的可靠性.温度扫描试验的应变水平均为0.003%,以确保试验在材料的线粘弹区域内进行.
2.2 试验数据处理与分析试验数据的处理仍采用Boltzmann模型拟合并计算得到沥青混合料玻璃态转变温度.处理后的试验结果汇总见表 9.对试验结果进行双因素等重复试验的方差分析,方差分析结果见表 10.
| 表 9 多因素试验结果 Tab. 9 Result of multi-factor experiment |
| 表 10 多因素试验方差分析结果 Tab. 10 Variance analysis of multi-factor experiment |
上表 8中SA表示升温速率的效应平方和;SB表示荷载速率的效应平方和;SA*B表示升温速率和荷载频率的交互效应平方和;SE为误差平方和;ST为总离差平方和.通过查表得F0.01(5, 72)=3.292、F0.01(25, 72)=2.049,即在0.01显著性水平下FA、FB、FA*B均大于相应的临界值.由此可知升温速率A、荷载频率B以及A×B均对试验结果有显著影响,并且升温速率与荷载频率的交互作用高度显著.
2.3 玻璃态转变温度预测模型为准确评价沥青混合料玻璃态转变温度随升温速率、荷载频率的变化规律,采用多元回归方法寻求动态模量与频率和升温速率的综合关系,将二维平面内的Tg-f、Tg-φ关系曲线拓展到三维Tg-f-φ坐标空间内.采用二维平曲面形式,对试验结果进行拟合,拟合结果为
| $z=13.8 x+1.84 y-0.74 x y-14.7. $ | (3) |
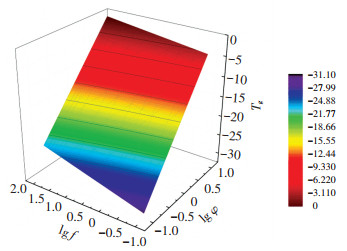
式中:z为沥青混合料的玻璃态转变温度;x为升温速率的对数值;y为荷载水平的对数值;拟合精度R2=0.97,该模型的曲面如图 8所示.
|
图 8 沥青混合料玻璃态转变温度曲面 Fig. 8 Surface of glass transition temperature of asphalt mixture |
由此可知,沥青作为一种典型的粘弹性材料,其玻璃态转变温度受升温速率、荷载频率的综合影响.在上述两因素的耦合作用下,沥青混合料的玻璃态转变温度在Tg-f-φ三维空间中呈平面分布,在低频和低升温速率下,其玻璃态转变温度较低,而在高频和高升温速率下玻璃态温度较高.而上述多因素下沥青混合料玻璃态转变温度预测模型的确立,提供了一种快速计算材料玻璃态转变温度的方法.
综合前述分析可知,荷载频率、升温速率对于沥青混合料的玻璃态转变温度存在显著影响,而沥青混合料的玻璃态转变温度在线粘弹性区域内并不存在明显的应变依赖性.鉴于大量的研究已经证明材料的玻璃态转变温度与其低温性能具有良好的相关性[12-20],因此可以预见在高升温速率、高荷载频率下,沥青混合料更容易发生低温破坏,而低升温速率和低荷载频率下,沥青混合料具有良好的变形能力,能够防止低温开裂的发生.
3 结论1) 采用Boltzmann模型拟合确定沥青混合料玻璃态转变温度的方法稳定且有效.
2) 沥青混合料的玻璃态转变温度随着升温速率的增大而升高,且玻璃态转变温度Tg与升温速率φ的对数值之间存在良好的线性关系.
3) 沥青混合料的玻璃态转变温度随着荷载频率的增大而升高,且玻璃态转变温度Tg与荷载频率f的对数值之间存在良好的线性关系.
4) 在线粘弹性范围内,沥青混合料的玻璃态转变温度在线粘弹性区域内并无明显的应变依赖性.
5) 升温速率与荷载频率对沥青混合料的玻璃态转变温度有显著影响,因此在测量材料玻璃态转变温度时需要根据材料在路面结构中的位置、材料服役地点的温度变化规律以及交通量水平确定试验的升温速率与荷载频率.
| [1] |
ZHANG Zhuyao, GRAHAM H, ADAM M. Properties of T/P92 weld metals for Ultra Super Critical (USC) power plant[J]. Microstructure Mater Properties, 2011, 6(1/2): 20. DOI:10.1504/IJMMP.2011.040435 |
| [2] |
TAN Yiqiu, GUO Meng. Study on the phase behavior asphalt mastic[J]. Construction and Building Material, 2013, 47: 311. DOI:10.1016/j.conbuildmat.2013.05.064 |
| [3] |
尹应梅.基于DMA方法的沥青混合料动态粘弹特性及剪切模量预估方法研究[D].广州: 华南理工大学, 2010 YIN Yingmei. Research on dynamic viscoclastic characteristics and shear modulus of prediction methods for asphalt mixture based on dynamic mechanical analysis (DMA) means[D]. Guangzhou: South China University of Technology, 2010 |
| [4] |
黄优, 刘朝辉, 李盛. 沥青材料玻璃态转变温度求解及低温性能分析[J]. 材料学报, 2016, 30(8): 141. HUANG You, LIU Zhaohui, LI Sheng. Glass transition temperature calculation and low temperature property analysis of asphalt[J]. Materials Review, 2016, 30(8): 141. |
| [5] |
常冠军. 粘弹性阻尼材料[M]. 北京: 国防工业出版社, 2012: 12. CHANG Guanjun. Viscoelastic damping materials[M]. Beijing: National Defense Industry Press, 2012: 12. |
| [6] |
何曼君, 陈维孝. 高分子物理[M]. 修订版. 上海: 复旦大学出版社, 2000: 241. HE Manjun, Chen Weixiao. Polymer chemistry[M]. Rev ed. Shanghai: Fudan University Press, 2000: 241. |
| [7] |
谭忆秋, 李晓琳, 吴建涛, 等. 温度及荷载频率对沥青-集料交互能力的影响[J]. 中国公路学报, 2012, 25(3): 65. TAN Yiqiu, LI Xiaolin, WU Jiantao, et al. Influence of temperature and loading frequency on the interaction ability of asphalt and aggregate[J]. China Journal of Highway and Transport, 2012, 25(3): 65. DOI:10.3969/j.issn.1001-7372.2012.03.005 |
| [8] |
AIREY G D, RAHIMZADEH B, COLLOP A C, et al. Linear viscoelastic limits of bituminous binders[J]. Asphalt Paving Technology: Association of Asphalt Paving Technologists-Proceedings of the Technical Sessions, 2002, 71: 89. |
| [9] |
SHAW M T, MACKNIGHT W J. Introduction to polymer viscoelastic[M]. 3rd ed. Wiley, New York: A John Wiley & Sons Inc. Publication, 1972.
|
| [10] |
谭忆秋. 沥青与沥青混合料[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007: 157. TAN Yiqiu. Asphalt and asphalt mixture[M]. Harbin: Harbin Institute of Technology Press, 2007: 157. |
| [11] |
赵选民. 试验设计方法[M]. 北京: 科学出版社, 2007: 16. ZHAO Xuanmin. Method of experiment design[M]. Beijing: Science Press, 2007: 16. |
| [12] |
曹丽萍, 谭忆秋, 董泽蛟, 等. 应用玻璃化转变温度评价SBS改性沥青低温性能[J]. 中国公路学报, 2006, 19(2): 1. CAO Liping, TAN Yiqiu, DONG Zejiao, et al. Evaluation for low temperature performance of SBS modified asphalt using glass transition temperature[J]. China Journal of Highway and Transport, 2006, 19(2): 1. DOI:10.3321/j.issn:1001-7372.2006.02.001 |
| [13] |
金磊, 钱振东, 郑彧. 基于DMA方法的浇筑式沥青胶浆高温性能及评价指标[J]. 东南大学学报(自然科学版), 2014, 44(5): 1062. JIN Lei, QIAN Zhendong, ZHENG Yu. High temperature performance and evaluation index of gussasphalt mortar based on DMA method[J]. Journal of Southeast University(Nature Science Edition), 2014, 44(5): 1062. DOI:10.3969/j.issn.1001-0505.2014.05.033 |
| [14] |
KRIZ P, STASTNA J, ZANZOTTO L. Effect of low temperature isothermal conditioning on glass transition in asphalt binders[C]//Conference of the Canadian Asphalt Technical Association. Ontario: CTAA, 2007: 161
|
| [15] |
ANDERSON D, MARASTEANU M. Physical hardening of asphalt binders relative to their glass transition temperatures[J]. Transportation Research Record Journal of the Transportation Research Board, 1999, 1661(1): 27. DOI:10.3141/1661-05 |
| [16] |
SOLIMAN H, SHALABY A. Characterizing the low temperature performance of hot-pour bituminous sealants using glass transition temperature and dynamic stiffness modulus[J]. Journal of Materials in Civil Engineering, 2009, 21(11): 688. DOI:10.1061/(ASCE)0899-1561(2009)21:11(688) |
| [17] |
NAM K, BAHIA H U. Effect of binder and mixture variables on glass transition behavior of asphalt pavement[J]. Association Asphalt Pavement Technologists, 2004, 73: 89. |
| [18] |
詹小丽.基于DMA方法对沥青粘弹性能的研究[D].哈尔滨: 哈尔滨工业大学, 2007 ZHAN Xiaoli. Research on the viscoelastic properties of asphalt using DMA [D]. Harbin: Harbin Institute of Technology, 2007 |
| [19] |
董雨明.硬质沥青及其混合料流变特性与低温性能研究[D].哈尔滨: 哈尔滨工业大学, 2015 DONG Yuming. Research on rheologigal property and low temperature performance of hard grade bitumen and its mixture [D]. Harbin: Harbin Institute of Technology, 2009 |
| [20] |
PELLINEN T K, WITCZAK M W, BONAQUIST R F. Asphalt mix master curve construction using sigmoidal fitting function with non-linear least squares optimization [C]//Engineering Mechanics Division Conference. New York: American Society of Mechanical Engineers, 2003: 83
|
 2019, Vol. 51
2019, Vol. 51


