2. 同济大学 交通运输学院,上海 200092
2. .College of Transportation Engineering, Tongji University, Shanghai 200092, China
沥青路面摊铺阶段作为施工过程的重要环节,容易出现混合料摊铺不均匀,导致离析的出现[1],路面的不均匀导致混合料的级配及沥青含量发生了变化,并造成路面结构性能变差[2].目前,国内外学者多数集中于研究沥青混合料均匀性对其物理、力学性能的影响,对于离析的检测,没有形成统一的标准及评价方法[3-5].传统的沥青混合料离析的检测方法费时费力且会对路面造成损害,加速路面局部的早期损害,并且均在路面铺筑完成后进行[6],不能快速地对面离析做出评价,且检测效率低.
近年来,由于数字图像处理技术具有快速,准确、自动化水平高等优点,在交通运输行业中得到广泛的应用[7].文献[8]通过数字图像处理技术表征了沥青混合料粗集料的细观结构,为沥青混合料数字图像处理技术研究的奠定了基础.文献[9]以三维图像处理技术为核心,运用数字图像处理技术对沥青混合料内部结构进行识别研究.文献[10]运用国外先进检测设备红外热像仪对沥青路面温度离析进行检测,提出了采用数字图像处理技术评价沥青混凝土的离析方法.本文尝试将数字图像处理技术引入沥青混合料摊铺均匀性的评定,提出一种快速、准确、全面的摊铺沥青路面均匀度评价方法.
1 沥青混合料数字图像的预处理为使沥青混合料图像可以进行分析计算,需要对采集到的图像进行预处理[11].本文依托玉溪至楚雄高速公路工程建设项目,在下面层AC-25型沥青混合料摊铺施工时采集照片,筛选1 085幅照片进行处理分析,以YC-001为例,如图 1所示,YC表示玉楚高速采集沥青路面图像,001表示图像编号.

|
图 1 YC-001原始图像 Fig. 1 Original image (YC-001) |
通过MATLAB软件中数字图像处理工具将沥青路面原始图像进行预处理,预处理步骤:1)将采集的RGB图像转化为灰度图像;2)对灰度图像进行自适应滤波,消除外界噪声干扰,改善图像质量;3)通过直方图均衡化增强图像的对比度,利于颗粒边缘识别;4)将直方图均衡化后的图像进行形态学处理和分水岭分割从而对集料颗粒进行识别与粘连颗粒分割,最终得到二值图像.预处理后的沥青路面二值图像如图 2所示.

|
图 2 形态学处理后的二值图像 Fig. 2 Binary image after morphology processing |
以往的沥青路面摊铺均匀性研究发现:粗集料的分布状态对沥青路面均匀性有重要影响,而细集料由于颗粒较小、数量众多,基本不存在离析问题,对均匀性评价结果影响不大,因此在图像处理中可以过滤小面积颗粒,只研究粗集料的分布状态[12].
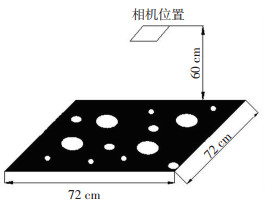
对于玉楚高速公路下面层AC-25粗粒式沥青混凝土,只考虑粒径9.5 mm以上粗集料分布均匀性的影响.沥青路面图像采集示意图如图 3所示.采集沥青路面图像时光照均匀,照相机距离路面60 cm的高度垂直路面向下拍摄,每张图片拍摄的沥青路面尺寸为72 cm×72 cm.假设集料颗粒为圆形颗粒密度相同[13],像素尺寸与实际尺寸对应关系为
|
图 3 沥青路面采集示意图 Fig. 3 Schematic diagram of asphalt pavement acquisition |
| $\frac{4 P}{2448^{2}}=\frac{{\rm{ \mathit{ π} }} d^{2}}{72^{2}} \times 10^{-2}. $ | (1) |
由式(1)计算得出,本文采集沥青路面图像9.5 mm粒径对应像素值为819,13.2 mm粒径对应像素值为1 582,16 mm对应像素值为2 324,19 mm粒径对应像素值为3 277,26.5 mm粒径对应像素值为6 376.
定义沥青路面的颗粒面积比A,描述图像对应区域中不同粒径粒料面积占此区域总面积的比值,即
| $A=\frac{\sum\limits_{i=1}^{n} P_{i}}{Z^{2}}. $ | (2) |
式中Pi为图像中各档集料每个集料颗粒的像素值,Z为二值图像的行列数.
2.2 沥青路面的颗粒面积比计算结果与分析沥青路面颗粒面积比的计算步骤:1)计算出粒径9.5 mm以上集料的颗粒面积比;2)分别计算出粒径9.5~13.2 mm、13.2~16 mm、16~19 mm、19~26.5 mm、26.5~31.5 mm各档集料颗粒面积比.
通过对比沥青路面图像上各档集料颗粒的面积比与AC-25原始路面各档集料颗粒的面积比,验证数字图像处理方法准确性.玉楚高速公路下面层采用AC-25粗粒式沥青混凝土,其合成级配见表 1.
| 表 1 AC-25合成级配 Tab. 1 Composite gradation of AC-25 |
假设沥青路面集料分布均匀、颗粒形状为圆形,由不同集料密度、质量大致推算出各档集料的颗粒面积比见表 2.
| 表 2 均匀分布下沥青路面的颗粒面积比 Tab. 2 Particle area ratio of asphalt pavement under uniform distribution |
由表 2可得图像处理法均匀分布下沥青路面的颗粒面积比相差7.58%,结果验证了采用的图像处理方法对于沥青路面摊铺均匀度分析的适用性和可靠性.
3 沥青混合料均匀性算法 3.1 基于四边静矩理论的模型建立对于二值图像上集料颗粒的分布状态,考虑到颗粒分布的均匀性与颗粒大小、位置有关,建立基于四边静矩理论的模型,进行沥青路面集料均匀性定量分析.静矩又称为截面面积矩,表示平面图形的面积A与其形心到某一坐标轴距离的乘积,一般用S来表示,即
| $S=A \times l. $ | (3) |
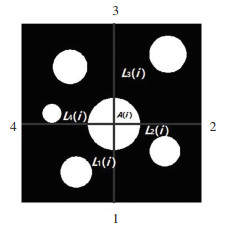
为了简化模型,方便后续计算和结果分析,作出如下假设:1)图像预处理后集料颗粒形状没有改变;2)只考虑粗集料分布状态;3)图像区域内集料颗粒的形状均为圆形且互不重叠.颗粒实际分布状态模型如图 4所示.
|
图 4 颗粒实际分布状态 Fig. 4 Actual distribution of particles |
由图 4可知,集料颗粒对第1、2、3、4条边的静矩和分别为
| $\begin{aligned} \bar{S}=& \frac{S_{1}+S_{2}+S_{3}+S_{4}}{4}=\\ & \sum\limits_{i=1}^{n} A(i) \times \frac{l_{1}(i)+l_{2}(i)+l_{3}(i)+l_{4}(i)}{4}=\\ & \sum\limits_{i=1}^{n} A(i) \times \frac{a}{2} \end{aligned} $ | (4) |
其中A(i)为第i个集料颗粒的面积;l1(i)、l2(i)、l3(i)、l4(i)为第i个集料颗粒到4条边的距离;a为图像对应区域的边长.
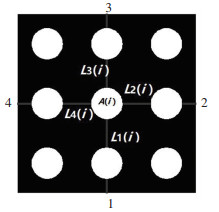
由式(4)得出,S只和集料颗粒总面积、正方形边长有关,所以对于同一二值图像,S是一个定值.将实际分布的集料颗粒按总面积相等均匀分布在二值图像上,得到颗粒理想均匀分布状态,如图 5所示.
|
图 5 颗粒理想均匀分布状态 Fig. 5 Ideal uniform distribution of particles |
由图 5可知,理想分布状态下的平均静矩和S为
| $\bar{S}=S_{1}=S_{2}=S_{3}=S_{4}=\sum\limits_{i=1}^{n} A(i) \times l_{1}(i). $ | (5) |
由式(5)可以看出,按照总面积相等原则,理想均匀分布状态下的S等于实际分布状态下的S,同时,S能够代表理想均匀分布下集料颗粒对每一条边的静矩和.定义静矩标准差DS为二值图像上集料颗粒对每条边的静矩和S(i)与理想均匀分布下集料颗粒对每条边的静矩和S的离差平方和的算术平均数的平方根,反映实际状态下每条边的静矩和与理想均匀分布下静矩和的离散程度,即
| $D_{\mathrm{S}}=\sqrt{\frac{\sum\limits_{i=1}^{4}\left(S_{i}-\bar{S}\right)^{2}}{4}}. $ | (6) |
由式(6)可知,静矩标准差的值越大,集料颗粒对每条边的静矩和与理想均匀分布下静矩和之间差异越大,沥青路面集料分布越不均匀.
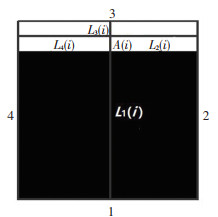
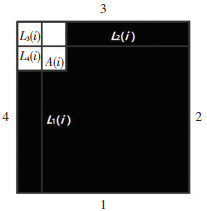
颗粒最不均匀分布状态.假设两种集料颗粒最不均匀分布状态,分别为图像区域内所有集料颗粒集中一条边分布,如图 6所示;以及图像区域内所有集料颗粒集中于一个角分布,如图 7所示.
|
图 6 颗粒集中一边分布 Fig. 6 Schematic diagram of particles' concentrated distribution on one side |
|
图 7 颗粒集中一角分布 Fig. 7 Schematic diagram of particles' concentrated distribution on a corner |
集料颗粒集中于一条边分布时静矩标准差DS1大于集料颗粒集中于一个角分布的静矩标准差DS2,由于静矩标准差DS值越大,颗粒分布越不均匀.当集料颗粒全部集中分布在正方形的一条边或一个角时,每条边的静矩和与理想均匀分布下静矩和的离散程度最大,颗粒分布最不均匀.
3.2 沥青混合料摊铺均匀度的定义由于二值图像上像素点数量过多,计算得到的静矩标准差DS值过大,用静矩标准差DS来表征集料均匀性不方便,评价标准不易确定.因此,考虑将静矩标准差DS数据标准化.本文采用Min-max标准化进行数据处理,以理想均匀分布状态下的静矩标准差DS为最小值,即DSmin;以最不均匀分布状态下的静矩标准差DS为最大值,即DSmax.将实际分布状态下的静矩标准差DS按线性变换映射到[0, 1]之内,使得数据标准化处理更加方便快捷.
定义:沥青路面摊铺均匀度为
| $U_{\mathrm{A}}=\frac{D_{\mathrm{S}_{\max }}-D_{\mathrm{S}}}{D_{\mathrm{S}_{\max }}-D_{\mathrm{S}_{\min }}}=1-\frac{D_{\mathrm{S}}}{D_{\mathrm{S}_{\max }}}. $ | (7) |
式中:DS为实际分布状态下静矩标准差;DSmax为最不均匀分布状态下静矩标准差;DSmin为理想均匀分布状态下静矩标准差,DSmin=0;
由式(7)得出,沥青路面摊铺均匀度的取值范围为0≤UA≤1,UA越接近1表示沥青路面越均匀,UA越接近0表示沥青路面越不均匀.
3.3 沥青路面摊铺均匀度评价标准文献[14-15]通过对切割圆柱试件截面进行分析,研究结果表明试件顶部到底部颗粒分布规律并无明显变化,因此本文采用沥青混合料表面颗粒分布状况进行均匀性评价.
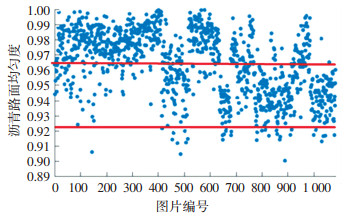
将照相机采集的1 085张玉楚高速公路沥青路面下面层摊铺时的照片用MATLAB软件进行图像处理,同时采用基于四边静矩理论模型,计算其沥青路面摊铺均匀度UA.现场采集1 085张沥青路面图像的摊铺均匀度UA散点图如图 8所示.
|
图 8 沥青路面摊铺均匀度散点图 Fig. 8 Scatter diagram of asphalt pavement paving uniformity |
通过对比结果得出,第145号图UA=0.905 885最小,第99号图UA=0.998 294最大,分别绘制出第145、99、9、144号图像,如图 9所示.

|
图 9 实际图像均匀度结果对照图 Fig. 9 Uniform distribution of actual image |
为减少钻芯取样和燃烧炉法温度过集料破碎造成的影响,分别对9、99、144、145号图像对应的路段分别取两个样本点进行钻芯取样,采样直径为100 mm,对应试件编号分别为9-1、9-2、99-1、99-2、144-1、144-2、145-1、145-2.将钻芯样本通过燃烧炉法确定配合比.样本重新筛分后级配见表 3.
| 表 3 燃烧炉法后钻芯芯样级配配合比 Tab. 3 Mixture ratio of the drilling core samples after burning |
由表 3可知,145号图两芯样级配呈明显差别,并且不符合规范标准,表明集料分布非常不均匀,其UA=0.905 885最小;而第99号两芯样级配并无明显差别,集料颗粒分布均匀,此时UA=0.998 294最大;第9号图和第144号图两芯样级配差别较小,集料颗粒分布较为均匀,UA值分别为0.945 591和0.982 355.因此,结合表 3中芯样级配对比结果和散点图中UA值数据得密集程度,得出UA值处于[0.96, 1]时,沥青路面均匀;UA值处于[0.92, 0.96]时,沥青路面较为均匀;UA值处于[0, 0.92]时,沥青路面不均匀.
4 结论1) 将数字图像处理基于应用于沥青沥青混合料摊铺均匀性评价中,通过运用MATLAB软件将现场采集的1 085张AC-25沥青混合料图像进行预处理,并通过计算预处理后图像中颗粒面积比进行验证,结果表明图像中9.5 mm以上的颗粒面积比为0.365,经过图像预处理后的沥青路面数字图像能够较好的反映原图像的颗粒分布状态;
2) 通过计算预处理后图像中9.5 mm以上颗粒对四条边的静矩和标准差,并min-max标准化,分析现场图像标准化静矩和标准差分布规律,得出均匀度评价指标,即UA值处于[0.96, 1]时,沥青路面均匀;UA值处于[0.92, 0.96]时,沥青路面较为均匀;UA值处于[0, 0.92]时,沥青路面不均匀.
3) 对图像对应区域进行钻心取样并通过燃烧炉法后进行筛分,重新筛分级配结果与本文图像法评价沥青路面摊铺均匀性结果一致,结果表明采用静矩标准差评价沥青混合料颗粒分布均匀性具有较高的可靠性和准确性.
| [1] |
丛林, 郑晓光, 郭忠印. 施工离析对沥青混合料性能的影响分析[J]. 同济大学学报(自然科学版), 2007, 35(4): 477. CONG Lin, ZHENG Xiaoguang, GUO Zhongyin. Influence of segregation in construction on asphalt mixture performance[J]. Journal of Tongji University (Natural Science), 2007, 35(4): 477. DOI:10.3321/j.issn:0253-374X.2007.04.009 |
| [2] |
BROCK J D. Segregation of asphaltic mixtures (with discussion)[C]//Association of Asphalt Paving Technologists Proc. [S.l.]: AAPT, 1985: 269
|
| [3] |
彭勇, 孙立军. 沥青混合料均匀性(离析)研究方法概述[J]. 中外公路, 2007, 27(1): 147. PENG Yong, SUN Lijun. A summary of research method of homogeneity of asphalt mixture[J]. Journal of China and Foreign Highway, 2007, 27(1): 147. DOI:10.3969/j.issn.1671-2579.2007.01.037 |
| [4] |
叶飞.路面混合料的离析评价方法研究[D].西安: 长安大学, 2012 YE Fei. Study on the appraisal of the pavement mixture segregation[D]. Xi'an: Chang'an University, 2012 |
| [5] |
唐娴, 王社良, 戴经梁. 沥青混合料离析的评价模型与评价标准[J]. 交通运输工程学报, 2010, 10(2): 1. TANG Xian, WANG Sheliang, DAI Jingliang. Evaluated model and standard of segregation for asphalt mixture[J]. Journal of Traffic and Transportation Engineering, 2010, 10(2): 1. DOI:10.3969/j.issn.1671-1637.2010.02.001 |
| [6] |
STROUP-GARDINER M, BROWN E R. Segregation in Hot-mix asphalt pavement[R]. Washington DC: National Academy Press, 2000
|
| [7] |
YUE Z Q, BEKKING W, MORIN I. Application of digital image processing to quantitative study of asphalt concrete microstructure[R]. Washington DC: Transportation Research Board, National Research Council, 1995: 53
|
| [8] |
YUE Z Q, MORIN I. Digital image processing for aggregate orientation in asphalt concrete mixtures[J]. Canadian Journal of Civil Engineering, 1996, 23: 479. |
| [9] |
SIMAP Team. Simulation imaging and mechanics of asphalt pavement[R]. Georgetown Pike: U.S. Department of Transportation Federal Highway Administration, 1998
|
| [10] |
郭大进, 沙爱民, 孙建华, 等. 运用红外热像仪改善沥青混合料温度离析效果的研究[J]. 公路交通科技, 2007, 24(5): 63. GUO Dajin, SHA Aimin, SUN Jianhua, et al. Research on the application of infrared thermal camera in asphalt pavement segregation analysis[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 63. DOI:10.3969/j.issn.1002-0268.2007.05.015 |
| [11] |
全红艳, 曹桂涛. 数字图像处理原理与实现方法[M]. 北京: 机械工业出版社, 2014. QUAN Hongyan, CAO Guitao. Principles and implementations of digital image processing[M]. Beijing: China Machine Press, 2014. |
| [12] |
秦雯.基于颗粒物质特性的路面材料离析过程研究[D].西安: 长安大学, 2011 QIN Wen. Study on segregation of pavement materials based on granular characteristics[D]. Xi'an: Chang'an University, 2011 |
| [13] |
李想, 梁乃兴, 赵毅. 基于数字图像技术沥青路面集料离析的研究[J]. 中外公路, 2014, 34(4): 90. LI Xiang, LIANG Naixing, ZHAO Yi. Research on segregation of asphalt pavement based on digital image processing technology[J]. Journal of China and Foreign Highway, 2014, 34(4): 99. |
| [14] |
吴文亮, 赵超, 田恒辽, 等. 考虑级配离析情况下燃烧炉法测定沥青含量的研究[J]. 公路工程, 2016, 41(5): 92. WU Wenliang, ZHAO Chao, TIAN Hengliao, et al. Study on combustion furnace method to test asphalt content considering the aggregate segregation[J]. Highway Engineering, 2016, 41(5): 92. DOI:10.3969/j.issn.1674-0610.2016.05.019 |
| [15] |
杜镇宇, 梁乃兴, 赵毅. 数字图像技术分析沥青路面均匀性方法[J]. 中外公路, 2017, 37(5): 62. DU Zhenyu, LIANG Naixing, ZHAO Yi. Method for analyzing the uniformity of asphalt pavement by digital image technology[J]. Journal of China and Foreign Highway, 2017, 37(5): 62. |
 2019, Vol. 51
2019, Vol. 51


