2. 哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
粗集料的形态特征包括形状,大小,角度和表面纹理[1].在机械载荷作用下,集料的形态特征对沥青混凝土的整体响应起着重要作用,而粗集料的表面纹理是影响沥青路面表面性能的关键因素[2].通过摄影测量和形态学技术对粗集料表面纹理进行分析[3],是沥青混合料研究的热点.沥青路面的抗滑性能[4]、抗磨光性能[5]及抗车辙性能[6]等直接受粗集料表面纹理的影响.因此,寻求粗集料表面纹理定量表征方法,选择合适的粗糙度评价指标,对于指导实际工程从而提高沥青混合料的路用性能具有重要意义.
文献[7]采用表面轮廓测量系统对磨光前后集料表面微观纹理的变化进行研究,结果表明标准粗糙度参数Sa可以很好地描述磨光前后纹理的变化.文献[8]采用离散傅里叶变换方法,使用纹理因素TF对集料的纹理特性进行表征,结果表明随着TF增大,车辙深度变大,使用表面更粗糙的粗集料可提高SMA抗车辙能力.文献[9]为了更好地评估不同波长的作用,将粗集料微观纹理(0.05~0.5 mm)和宏观纹理(0.5~2.56 mm)分别分成4个和两个波长带,采用功率谱密度函数PSD分析了集料微观纹理,用均方根粗糙度Rq和表面光滑深度Rp表征摩擦性能,结果表明0.05~0.25 mm的纹理波长能显著提高表面的摩擦性能.文献[10]采用二维功率谱密度2D-PSD评估磨光前后表面粗糙度和纹理变化,结果表明磨光仅在非常短的波长(<62.8 μm)下影响表面纹理.文献[11-12]采用Micro-Deval测试集料的抗磨光性能,并采用纹理指数TI表征表面纹理特性,结果表明纹理变化对磨光时的质量损失仅有很小的影响.考虑到现有测量系统都是从二维出发进行集料纹理评价,文献[13]等人开发了三维纹理开发程序MicroSYS,采用Z平面体积差异参数表征集料纹理特性,但参数的有效性还有待验证.文献[14]通过立体显微镜扫描集料颗粒,并使用Nis Elements D软件创建集料的3D图像,通过软件的交互式测量工具从3D图像获取集料轮廓.计算轮廓高程分布的平均算术偏差Ra,均方根Rq,偏度Rsk和峰度Rku,该方法显示了从单个集料获得的不同轮廓之间统计特性的可变性.目前学者们已经研究了多种测量方法和表征参数描述粗集料表面纹理,但考虑到纹理波长(微米级),准确定量的描述仍然很有困难.
集料表面纹理在一定的尺度范围内呈现出统计意义上的自相似性[15],即具有分形特性.分形是定量描述自然界不规则现象或物体的一种数学语言,它用于表示在不同尺度下,纹理具有相似结构的特性.文献[16]采用多种分维计算方法对花岗岩、玄武岩、石灰岩等粗集料表面轮廓线进行分析,结果表明粗集料表面纹理分形维数越大则粗糙程度越复杂.文献[17]采用激光轮廓仪对粗集料表面纹理曲线进行直接测量,通过轮廓滤波方法将纹理曲线分为宏观纹理和微观纹理(波长界限为2 mm).运用分形理论中对随机过程的结构函数方法,验证了表面纹理曲线的分形特性,并采用分形维数D和截距K作为评价指标定量描述粗集料的表面纹理粗糙度[18-19].但分形维数作为一个整体指标,只能反映出物体的全局特征而不能表征局部奇异性[20],且不同方法求出的分维数也不相同.此外,由文献中数据不难看出,分形维数对粗集料粗糙度不敏感,不同集料纹理曲线的分形维数差别不明显.鉴于此,亟待提出能准确全面地描述粗集料粗糙度的评价指标.文献[21]在研究硬垫层与橡胶之间的摩擦时提出了高差相关函数,结果表明相关参数可以很好地表征路面纹理特性.因此,考虑粗集料表面纹理的自相似性,本文尝试采用高差相关函数对粗集料表面纹理特性进行分析,采用自相似特征参数作为评价指标,多尺度表征厘米级到毫米级的粗集料表面纹理特性,实现不同种类集料纹理的识别.
1 理论分析 1.1 高差相关函数为了对表面纹理的粗糙度进行数学分析,假设断面轮廓高程z(x)是自仿射的,则对任意比例因子Λ,换算公式[22]为
| $ \left\{ {\begin{array}{*{20}{l}} {x \to \mathit{\Lambda} x, }\\ {z \to {\mathit{\Lambda} ^H}z.} \end{array}} \right. $ | (1) |
其中H为赫斯特指数,与分形维数D等效,对于轮廓曲线,D=2-H,0≤H≤1.
在式(1)中,使用的是二维符号.事实上,表面的自仿射特性可由相关函数描述,例如高差相关函数表示为
| $ C_{z}(\lambda)= <(z(x+\lambda)-z(x))^{2}>_{x} \sim \xi_{\perp}^{2}, $ | (2) |
式中 < …>x表示x方向上的平均值,Cz(λ)描述表面相对于水平方向的均方高度差,可以理解为一定尺度下表面的幅度方差期望值,对于自仿射曲面,在小尺度范围内,Cz(λ)遵循指数为2H=4-2D的幂定律,直至达到断面轮廓的幅度方差期望值
| $ C_{z}(\lambda)=\xi_{\perp}^{2}\left(\frac{\lambda}{\xi_{/ /}}\right)^{4-2 D}, \lambda <\xi_{/ /}. $ | (3) |
式(3)表明了小尺度范围内表面纹理的结构相似特性,而在大尺度范围下表面纹理呈现出显著的统计特性,则可得出表面幅度方差期望值
| $ C_{z}(\lambda)=\xi_{\perp}^{2}, \lambda \geqslant \xi_{/ /}. $ | (4) |
高差相关函数可对粗糙度进行多尺度表征,3个粗糙度参数D,
|
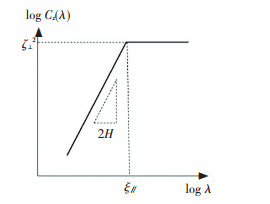
图 1 自仿射表面高差相关函数图 Fig. 1 Height difference correlation function for a self-affine surface |
在小尺度范围λ <
分形表面具有显著的分段分维特性,仅用单一的分形维数代表整个表面纹理尺度范围内的分形特性存在一定的局限性[23].对于粗集料,主要可从两个尺度研究其纹理特性:一是研究其微观纹理结构特性,二是研究最大微凸体的粗糙度.因此有必要引入两段变维分形,以更全面地描述粗集料表面纹理特性.两段变维分形的高差相关函数分别为
| $ C_{z}(\lambda)=\xi_{\perp}^{2}\left(\frac{\lambda}{\xi_{\mu}}\right)^{2 H_{1}}, \lambda_{2} <\lambda <\xi_{/ /}; $ | (5) |
| $ C_{z}(\lambda)=\xi_{\perp}^{2}\left(\frac{\lambda}{\lambda_{2}}\right)^{2 H_{2}}\left(\frac{\lambda_{2}}{\xi_{/ /}}\right)^{2 H_{1}}, \lambda <\lambda_{2}. $ | (6) |
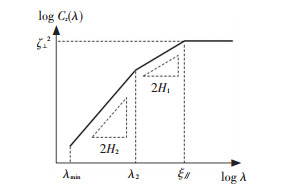
其中λ2可理解为两个尺度的水平波长界限,即微观纹理与宏观纹理的界限(见图 2),水平截止波长
|
图 2 两段变维分形相关函数图 Fig. 2 Height difference correlation function with a two scaling ranges approach |
选取粒径大小为9.5~13.2 mm的6种集料,分别为闪长岩、黄砂岩、花岗岩1、辉绿岩、花岗岩2、白云岩,其对应的磨光值依次为73、60、47、46、46、37.采用物镜60倍、目镜100倍的显微镜对集料表面进行60倍放大观察,集料特性见图 3.从图中可看出,不同种类的集料表面粗糙程度区别较为明显,其中闪长岩最为粗糙,白云岩相对最光滑.

|
图 3 粗集料表面放大图 Fig. 3 Magnification view of coarse aggregate surface |
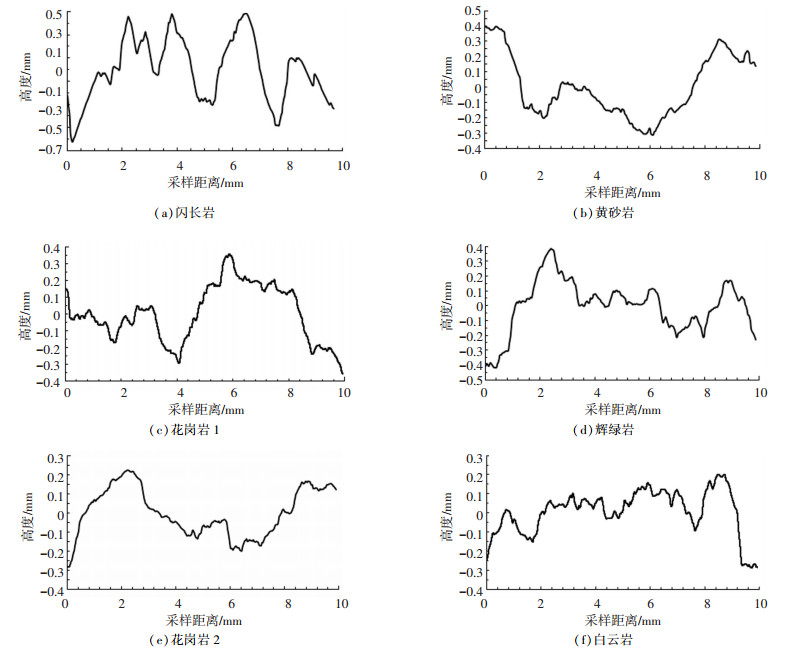
采用针描法获取集料表面轮廓曲线.试验仪器为MMD-R100D高精度轮廓仪,轮廓仪X轴测量精度为1.2 μm,光栅分辨率为0.1 μm,Z1轴测量精度为1 μm,分辨率为0.05 μm,测量速度为0.02~4 mm/s,满足集料表面形貌测量要求.测量过程中,将集料置于X方向上的精密气浮直线运动导轨,使触针与试件表面接触,通过测量系统进行设置,发出测量命令,计算机接受命令后驱动控制指令使X向运动导轨移动,集料沿X轴方向以采样间隔移动,在待测部位得到测量点的X坐标,此时触针随表面轮廓的起伏而上下移动,引起Z1轴的数字传感器输出电信号,该信号经光电转换处理电路传输至计算机进行处理,即为一个采集到的Z向坐标,重复该过程,即可得到集料表面轮廓曲线.测量仪器图及测量原理图如图 4所示.轮廓仪所采集的粗集料表面轮廓数据如图 5所示.

|
图 4 针描法测量粗集料表面轮廓曲线 Fig. 4 Needle drawing method for measuring the texture profile curve of the aggregate surface |

|
图 5 粗集料轮廓图 Fig. 5 Profile of coarse aggregate |
数据预处理主要是为了消除针描过程中的倾斜坡度误差及偏移误差.其中倾斜坡度误差来源于试件摆放不正,使得获取的粗集料表面轮廓线具有一定的倾斜坡度;偏移误差则是轮廓仪自身存在的测量误差造成.
令zi为xi处的样本i的测量信号值,N为评估信号内的样本数量,则表面轮廓的斜率b1的计算公式[24]为
| $ {b_1} = \frac{{12\sum\limits_{i = 0}^{N - 1} i {z_i} - 6(N - 1)\sum\limits_{i = 0}^{N - 1} {{z_i}} }}{{N(N + 1)(N - 1)}}, $ | (7) |
表面轮廓的偏移量b0的计算公式为
| $ {b_0} = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {{z_i}} - \frac{1}{2}{b_1}(N - 1), $ | (8) |
测量的信号值zi根据式(9)对斜率和偏移进行校正,得到校正采样信号值Zi为
| $ Z_{i}=z_{i}-b_{1} i-b_{0}, i=0、\cdots、N-1, $ | (9) |
这里表面轮廓被视为样本数量i的函数,而不是测量距离
|
图 6 误差消除效果图 Fig. 6 Effect diagram after error elimination |
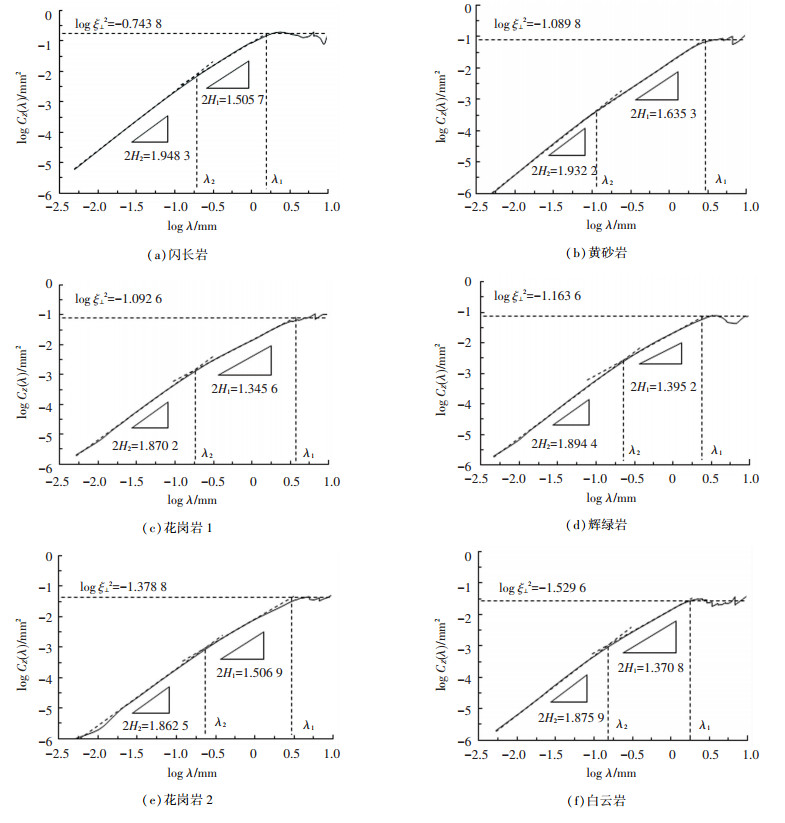
根据消除误差后的粗集料表面纹理数据,计算粗集料高差函数.各集料高差函数图如图 7所示.在log Cz(λ)与log λ的双对数曲线中,粗集料纹理曲线表现出较好的线性关系,表明粗集料表面纹理曲线在一定范围内具有分形特性.但随着尺度的增大,这种幂律关系逐渐减弱,直至
|
图 7 粗集料高差函数 Fig. 7 Height difference correlation function of coarse aggregate |
为分别求得其赫斯特指数H1和H2,需对曲线进行分段线性回归拟合.文献[21]表明赫斯特指数H或分形维数D取决于分段拟合时选择的区间间隔,分形维数随区间长度增大而增大.一般将区间设定为[5 μm, 100 μm]和[300 μm, 1 000 μm]进行拟合,拟合曲线的交点所对应的横坐标值即为λ2取值.文章根据粗集料表面纹理曲线形状,先将第一段拟合区间定为[5 μm, 100 μm],所对应的第二段拟合区间分别定为[300 μm, 1 000 μm]、[200 μm, 1 000 μm]、[150 μm, 1 000 μm]、[100 μm, 1 000 μm],拟合精度见表 1.
| 表 1 拟合精度对比图 Tab. 1 Comparison of fitting accuracy |
比较不同区间的拟合精度,可知区间[5 μm, 100 μm]和[300 μm, 1 000 μm]的拟合精度最高,最终选择区间[5 μm, 100 μm]进行第一段拟合,选择区间[300 μm, 1 000 μm]进行第二段拟合,拟合结果如图 7所示.由图 7可知,在小尺度区间[λ, λ2],粗集料粗糙度以斜率2H2递增,在大尺度区间[λ2,
| 表 2 粗集料表面参数 Tab. 2 Surface parameters of coarse aggregate |
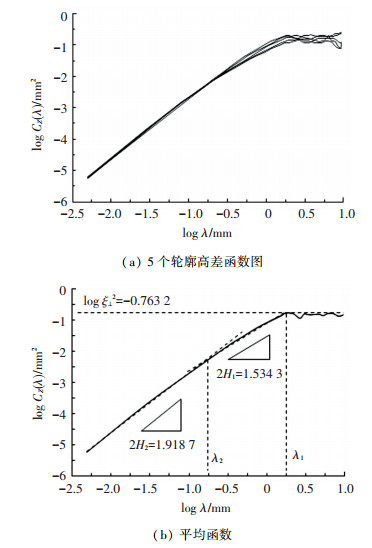
为全面反映粗集料表面纹理状况,对每个集料采集不同方向的5条轮廓曲线计算高差函数,求其平均函数并按照上述方法计算自相似特征参数,图 8以闪长岩为例.其中图 8(a),轮廓测量在不同方向进行,所求粗糙度具有典型的准各向同性特征,数据具有可重复性.图 9为粗集料微观与宏观分形维数平均值对比,图 10为各集料水平波长和幅度期望平均值对比.
|
图 8 闪长岩高差函数计算 Fig. 8 Height difference function calculation of diorite |
|
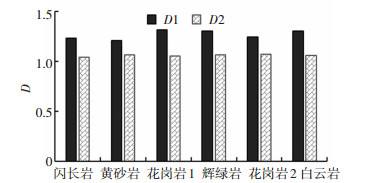
图 9 粗集料微观与宏观分形维数对比 Fig. 9 Comparison of micro texture and macro texture fractal dimensions of coarse aggregate |
|
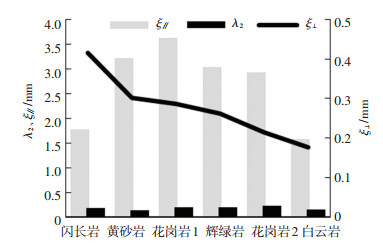
图 10 各集料尺寸参数平均值 Fig. 10 Wavelength parameters of coarse aggregate |
由图 9可知,集料宏观纹理与微观纹理的分形维数具有明显差异,各集料微观纹理分形维数均在1.05左右,宏观纹理分形维数均在1.3左右,各集料间差异不大.对于微观纹理,由于波长较小,粗糙程度相差不大,因而分形维数几乎相等;然而粗糙程度相差很大的集料,宏观纹理分形维数也相差不大,这说明分形维数对粗集料表面纹理粗糙水平不敏感.此外,若仅用分形维数作为独立参数来表达粗集料表面的粗糙程度,则存在分形维数与粗糙度唯一对应的问题[25].事实上,由D=2-H,则知只要两条直线平行,就会得到相等的分形维数,但这不能证明两个表面的粗糙度相等.导致分形维数与粗糙度不能唯一对应的原因,在于分形测量属于对轮廓曲线的相似性测量,分形维数是一种相对性的描述参数,它与测度绝对值的高低基本无关,而与多尺度测度的相对值存在依赖关系.因此,分形维数必须结合其他参数,才能准确表征粗糙程度.
由图 10可知,λ2为粗集料微观纹理与宏观纹理的界线,均在100~200 μm之间.到目前为止,在文献中没有关于长度尺度上的粗集料微观和宏观纹理的准确定义.尽管如此,它们的共同波长通常位于几百微米左右[22],因而100~200 μm应是可信的结果,另外,从岩石的结构特性来看,黄砂岩属于沉积岩,表面颗粒大小为0.05~2 mm, 试验结果为0.137 1 mm,符合实际情况;白云岩为细粒或中粒结构,表面为微细晶,因而λ2值也较小;试验用闪长岩、辉绿岩和花岗岩均属于岩浆岩,闪长岩为全晶质中性深成岩,中粒至粗粒结构,辉绿岩为浅成岩,显晶质,细-中粒结构,花岗岩为深成岩,晶体较粗大,为粗粒至巨粒结构,因此λ2值均较大;
1) 粗集料表面纹理在一定尺度范围内具有两段变维特性,粗集料微观纹理与宏观纹理的界线在100~200 μm左右,集料宏观纹理与微观纹理的分形维数具有明显差异,不同集料之间宏观纹理分形维数和不同集料之间微观纹理分形维数差异均不明显.分形维数对粗集料表面的粗糙程度不敏感,采用分形维数作为独立参数评价粗集料表面粗糙度具有很大局限性.
2) 根据水平截止波长
3) 由分形维数D,水平截止波长
| [1] |
ZHANG Dong, HUANG Xiaoming, ZHAO Yongli. Investigation of the shape, size, angularity and surface texture properties of coarse aggregates[J]. Construction & Building Materials, 2012, 34(34): 330. |
| [2] |
ARAGÃO F T S, PAZOS A R G, MOTTA L M G D, et al. Effects of morphological characteristics of aggregate particles on the mechanical behavior of bituminous paving mixtures[J]. Construction & Building Materials, 2016, 123: 444. |
| [3] |
BANGARU R S. Aggregate shape characterization in frequency domain[J]. Construction & Building Materials, 2012, 34(5): 554. |
| [4] |
REGINALD B K, EYAD A, KASSEM E, et al. A state-of-the-art review of parameters influencing measurement and modeling of skid resistance of asphalt pavements[J]. Construction & Building Materials, 2016, 114(7): 602. |
| [5] |
HUANG Chengyi. Texture characteristics of unpolished and polished aggregate surfaces[J]. Tribology International, 2010, 43(1/2): 188. |
| [6] |
CHUN S, KIM K, PARK B, et al. Evaluation of the effect of segregation on coarse aggregate structure and rutting potential of asphalt mixtures using Dominant Aggregate Size Range (DASR) approach[J]. KSCE Journal of Civil Engineering, 2017(6): 1. |
| [7] |
DUNFORDA M, PARRY A R, SHIPWAY P H, et al. Three-dimensional characterisation of surface texture for road stones undergoing simulated traffic wear[J]. Wear, 2012, 292(15): 188. |
| [8] |
LIU Yufeng, HUANG Yucheng, SUN Wenjuan, et al. Effect of coarse aggregate morphology on the mechanical properties of stone matrix asphalt[J]. Construction & Building Materials, 2017, 152: 48. |
| [9] |
KOUCHAAKI S, ROSHANI H, PROZZI J A, et al. Evaluation of aggregates surface micro-texture using spectral analysis[J]. Construction & Building Materials, 2017, 156: 944. |
| [10] |
WANG Dawei, LIU Pengfei, WANG Hao, et al. Modeling and testing of road surface aggregate wearing behaviour[J]. Construction & Building Materials, 2017, 131: 129. |
| [11] |
WANG Dawei, WANG Hainian, BU Yin, et al. Evaluation of aggregate resistance to wear with Micro-Deval test in combination with aggregate imaging techniques[J]. Wear, 2015, 338. |
| [12] |
WU Jiangfeng, HOU Yue, WANG Linbing, et al. Analysis of coarse aggregate performance based on the modified Micro Deval abrasion test[J]. International Journal of Pavement Research & Technology, 2018, 11: 185. |
| [13] |
ZUZANA F, MICHAL J. Quantification of aggregate surface texture based on three dimensional microscope measurement[J]. Procedia Engineering, 2017, 192. |
| [14] |
FLORKOVÁ Z, KOMAĈKA J. Usage of microscope method for detection of aggregate microtexture[J]. Procedia Engineering, 2015, 111. |
| [15] |
周兴林, 肖神清, 肖旺新, 等. 粗集料表面纹理粗糙度的多重分形评价[J]. 华中科技大学学报(自然科学版), 2017, 42(2): 29. ZHOU Xinglin, XIAO Shenqing, XIAO Wangxin, et al. Multi-fractal evaluation on roughness of coarse aggregate surface texture[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 42(2): 29. |
| [16] |
张肖宁, 孙杨勇. 粗集料表面纹理轮廓线分形分析及不同维数算法探讨比较[J]. 公路, 2010(12): 124. ZHANG Xiaoning, SUN Yangyong. Analysis of fractal of micro-structure curve of coarse aggregate and contrast between different dimension algorithms[J]. Highway, 2010(12): 124. |
| [17] |
周纯秀, 陈国明, 谭忆秋. 集料表面纹理粗糙度的测量[J]. 交通运输工程学报, 2009, 9(1): 50. ZHOU Chunxiu, CHEN Guoming, TAN Yiqiu. Roughness measurement of aggregate surface texture[J]. Journal of Traffic and Transportation Engineering, 2009, 9(1): 50. DOI:10.3321/j.issn:1671-1637.2009.01.011 |
| [18] |
周纯秀, 陈国明, 谭忆秋. 粗集料表面纹理粗糙度的分形测量和描述[J]. 哈尔滨工业大学学报, 2009, 41(11): 85. ZHOU Chunxiu, CHEN Guoming, TAN Yiqiu. Fractal Measurement and characterization on roughness of coarse aggregates surface texture[J]. Journal of Harbin Institute of Technology, 2009, 41(11): 85. DOI:10.3321/j.issn:0367-6234.2009.11.018 |
| [19] |
陈国明, 周纯秀, 谭忆秋. 粗集料表面纹理的分形评定及沥青混合料性能试验[J]. 交通运输工程学报, 2009(4): 1. CHEN Guoming, ZHOU Chunxiu, TAN Yiqiu. Fractal evaluation of surface texture for coarse aggregate and performance test of asphalt mixture[J]. Journal of Traffic and Transportation Engineering, 2009(4): 1. DOI:10.3321/j.issn:1671-1637.2009.04.001 |
| [20] |
LOEHLE C, LI B L. Statistical properties of ecological and geologic fractals[J]. Ecological Modeling, 1996, 85(2/3): 271. |
| [21] |
GAL A L, KLVPPEL M. Investigation and modelling of rubber stationary friction on rough surfaces[J]. Journal of Physics Condensed Matter, 2007, 20(1): 15. |
| [22] |
TORBRUEGGE S. Characterization of pavement texture by means of height difference correlation and relation to wet skid resistance[J]. Journal of Traffic & Transportation Engineering, 2015, 2(2): 59. |
| [23] |
杨发.基于胎/路耦合的沥青路面抗滑性能研究[D].东南大学, 2014 YANG Fa. Analysis of asphalt pavement skid resistance based on tire-road coupling[D]. Southeast University, 2014 http://d.wanfangdata.com.cn/Thesis/Y2758394 |
| [24] |
Characterization of pavement texture by use of surface profiles-Part 4: Spectral analysis of surface profiles: ISO/TS 13473-4-2008[S]. London: British Standards Institute, 2008
|
| [25] |
葛世荣. 粗糙表面的分形特征与分形表达研究[J]. 摩擦学学报, 1997, 17(1): 73. GE Shirong. The fractal behavior and fractal characterization of rough surfaces[J]. Tribology, 1997, 17(1): 73. DOI:10.3321/j.issn:1004-0595.1997.01.011 |
 2019, Vol. 51
2019, Vol. 51


