2. 陇东学院 土木工程学院, 甘肃 庆阳 745000;
3. 海南省交通运输厅, 海口 570216;
4. 滁州学院 地理信息与旅游学院, 安徽 滁州 239000
2. School of Civil Engineering, Longdong University, Qingyang 745000, Gansu, China;
3. Department of Transport of Hainan Province, Haikou 570216, Hainan, China;
4. School of Geographic Information and Tourism, Chuzhou University, Chuzhou 239000, Anhui, China
目前,国内外学者对饱和砂土液化研究不少,但针对地震作用下砂土液化机理及其判别方法尚未形成统一观点[1-3].文献[4]基于国内外25次大地震中的344组场地液化实测资料,分析了修正标准贯入击数与饱和砂土抗液化强度之间的非线性关系,建立了饱和砂土液化极限状态曲线或抗液化强度临界曲线经验公式;文献[5]详述了基于静力触探测试的国内砂土液化判别的规范法;文献[6]介绍了基于距离判别分析方法砂土液化预测模型及应用;文献[7]将距离判别分析方法应用于砂土液化的预测问题中,建立了砂土液化预测的距离判别模型;文献[8]采用可拓学的物元模型和聚类分析原理,提出了饱和砂土地震液化判别的可拓聚类方法;文献[9]针对汶川8.0级地震显著的砂砾土液化现象,提出基于剪切波速的砂砾土液化判别方法;文献[10]基于Fisher判别理论建立了砂土液化可能性的Fisher判别分析(FDA)模型,选取烈度、震中距、地下水位、砂层埋深、标贯击数、平均粒径、不均匀系数、剪应力比8个实测特征指标作为FDA模型的预测指标;文献[11-12]以新疆巴楚—伽师Ms6.8级地震液化现场勘察和测试为基础,提出了新的砂土液化判别公式.由此看出,由于砂土地震液化预测的影响因素较多,要作到对砂土液化合理的评价,需要针对具体工程实际进一步开展研究.
铺前大桥是海南省重点建设工程,该桥位于强震、活动断层、强风、强腐蚀区海洋环境,50 a超越概率2%地震动峰值加速度为0.59g,50 a超越概率10%地震动峰值加速度为0.35g,地震设防烈度Ⅷ度,其设计地震动峰值国内外鲜有,桥址区存在较厚的饱和砂土层,地表以下厚度1.9~14.0 m粉细砂、5.2~18.5 m含砾中细砂等易液化土层,地震砂土液化问题突出[13].鉴于此,本文基于铺前大桥桥址区岩土分布特征,利用振动台模型试验模拟了饱和粉细砂液化发展过程,分析了不同地震动强度下饱和细粉砂层的超静孔隙水压力及孔压比的变化规律,对比讨论了常用的砂土液化判别方法,提出了强震作用下的饱和粉细砂液化判别指标,为铺前大桥基础的合理设计与施工提供科学依据,并为类似工程提供技术借鉴.
1 振动台模型试验设计 1.1 试验设备与相似比试验采用三向六自由度5 m×5 m地震模拟振动台,数据采集系统为太平洋6000DAS.振动台最大载重30 t,最大位移X、Y向±80 mm、Z向±50 mm,最大加速度X、Y向1.0g、Z向0.7g,主机箱具有128个通道.
选用叠层剪切式模型箱研究饱和粉细砂的液化特征,能较准确的模拟地震作用下自由场的震动反应[14].模型箱的长宽高分别为3.7、2.1、1.7 m,如图 1所示.试验的缩尺比例为1/25,其他物理量相似比见表 1.

|
图 1 叠层剪切式模型箱 Fig. 1 Laminated shear model box |
| 表 1 试验相似比 Tab. 1 Similarity constants of each physical quantity |
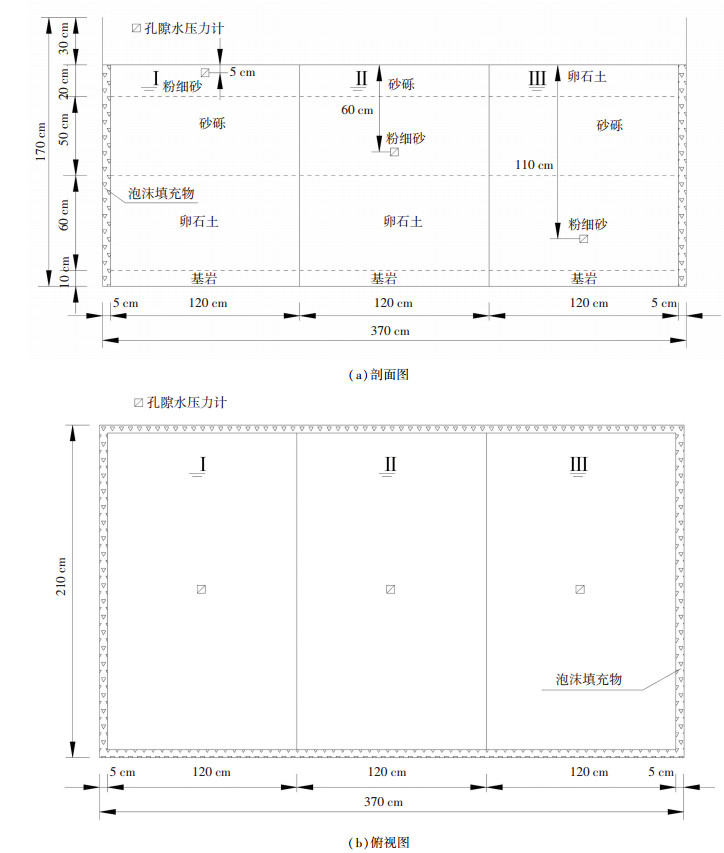
在保证模型试验可靠性的前提下,将模型箱划分为3个功能区,分别对应3种细粉砂层深度,在不同深度粉细砂层布设孔隙水压力计,土层分布及孔隙水压力计布设如图 2所示.
|
图 2 各功能区土层分布和孔隙水压力计布设 Fig. 2 Arrangement of soil layer distribution and pore water pressure gauge in each functional area |
基于铺前大桥的地质勘查资料,以土体剪切波速为主要控制指标,制作模型土.其中微风化花岗岩采用C60混凝土按照剪切波速和实际平均抗压强度62 MPa标准配制,测得其抗压强度(28 d)为58 MPa,与实际值接近.在模型箱中将土体浸泡24 h,待模型箱中水面不再下降,认为模型土完全饱和.粉细砂层、砂砾层、卵石层和微风化花岗岩的剪切波速分别为212、276、539、917 m/s.
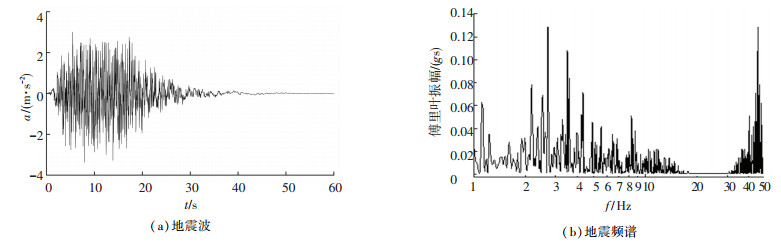
1.3 地震波选取中国地震局针对海南铺前大桥人工合成50 a超越概率10%,动峰值加速度0.35g的5010波.试验以5010波作为基准波,并采用地震波处理软件限制各地震动峰值加速度分别为0.15g、0.20g、0.25g、0.30g、0.35g、0.40g、0.45g、0.50g、0.55g、0.60g、0.80g[15]. 0.35g地震波及频谱如图 3所示.
|
图 3 地震波及频谱图 Fig. 3 Seismic spectrogram |
通过对饱和粉细砂液化振动台试验宏观现象的观察与记录,得到:当地震动强度为0.15g时,模型箱及模型土的反应较小,整体振动不明显,土层表面有少量水渗出,未出现明显喷砂冒水现象;当地震动强度为0.20g时,模型箱和模型土的振动逐渐变明显,土层表面有大量水渗出,土体产生明显的侧向位移,表层土产生裂缝,且土层表面出现不均匀沉降;当地震动强度≥0.25g(地震烈度Ⅷ度)时,表层的饱和粉细砂出现类似流体的运动特征,孔隙水从土体空隙中排出,同时伴有大量气泡冒出,且土层表面出现较明显的不均匀沉降,如图 4~6所示.

|
图 4 表层土产生裂缝 Fig. 4 Cracks in surface soil |

|
图 5 粉细砂开始液化 Fig. 5 Fine sand beginning to liquefy |

|
图 6 粉细砂完全液化 Fig. 6 Fine sand liquefaction |
可液化土振动过程中,孔压比(超静孔隙水压力与初始有效应力的比值)能比较准确的反映土体液化情况.不同深度下的粉细砂孔隙水压力μ、总应力σ及初始有效应力σ1见表 2.
| 表 2 不同深度饱和粉细砂初始有效应力 Tab. 2 Initial effective stress of fine sand with different depths |
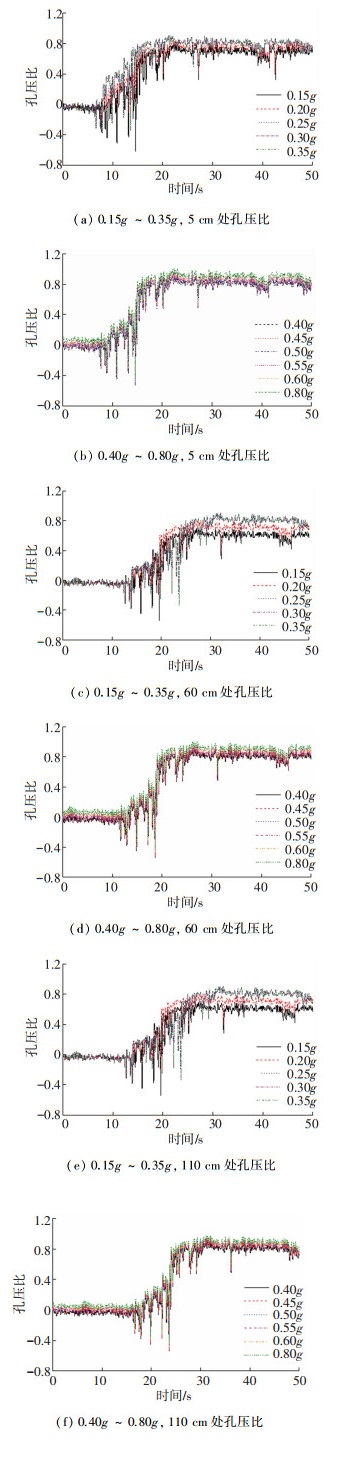
不同地震动强度、不同深度下的饱和粉细砂孔压比变化规律如图 7所示.
|
图 7 饱和粉细砂孔压比变化规律 Fig. 7 Variation of pore pressure ratio of saturated fine sand |
由图 7可看出,在不同地震动强度下,同一深度的饱和粉细砂孔压比变化规律相似.各地震动强度下,饱和粉细砂孔压比随地震动持时增加呈先在0附近震荡,而后快速震荡增加到一定值,最后趋于稳定,超静孔隙水压力增长滞后于地震动应力.
具体来讲,饱和粉细砂深度为5 cm时,各地震动强度下,超静孔隙水压力增长滞后于地震动应力9.7 s;地震动持时在9.7~22.8 s之间时孔压比呈迅速震荡增长;当地震动持时大于22.8 s后,孔压比趋于稳定.饱和粉细砂深度为60 cm和110 cm时,孔隙水压力增长分别滞后于地震动应力14.7 s和18.7 s,且分别在28.4 s和31.9 s后趋于稳定.说明浅层饱和粉细砂的超静孔隙水压力远小于深层饱和粉细砂的超静孔隙水压力,液化层上覆土层厚度越小,越容易液化,且在地震波加载完成后,浅层饱和粉细砂孔压比较深层饱和粉细砂孔压比达到稳定的时间更短.由于深层饱和粉细砂土孔隙水无法向四周扩散,只能向上进行渗流,导致上部孔隙水压力保持不变或小幅上升,上部粉细砂的孔压消散较慢,这与土层的渗透能力密切相关.
深度为5 cm、60 cm和110 cm的饱和粉细砂,当地震动强度分别≥0.15g、0.20g和0.25g时,孔压比稳定值均≥0.8.此时模型箱内土体出现大面积喷砂冒水现象,说明土体孔隙水在地震动作用下向上排出,导致土颗粒失重,当土体抗剪强度小时,土体完全液化.
此外,在地震波作用下,不同深度的饱和粉细砂孔压比均有负值出现,这是由于在地震动作用时,粉细砂发生剪胀现象,从而导致超静孔隙水压力呈现负增长,引起负孔压比的出现.
4 饱和粉细砂液化判别计算与讨论 4.1 常用液化判别方法的判定结果对比中国常用的饱和砂土液化判别方法主要为规范法和剪切波速法.其中文献[16]是根据邢台地震、通海地震、海城地震、唐山地震及国外大地震的资料和室内液化实验的研究成果,是基于实际地震时液化调查而建立的判别方法,缺乏理论基础,对深层地基土的判别结果偏于保守;文献[17]中通过计算不同深度处土层液化抵抗系数,利用计算模型中的桩土相互作用土弹簧的刚度进行折减来模拟砂土液化的影响,判别结果偏于安全;文献[18]中石兆吉法具有稳定性好、可在原位土层中进行测量等优点,但由于没有考虑上覆土层的土性、粘粒含量以及层厚等因素,具有一定的局限性;文献[19]中Seed判别法是通过研究砂土的循环阻力比与标准贯入试验建立关系得出的判别方法,该法判别计算复杂,在实际工程应用时工程技术人员不好运用,另外对深层地基土的判别也偏于不安全.
采用现行规范判别法和剪切波速法对铺前大桥桥址区粉细砂土层液化判别,抗震设防烈度为9度.公式中参数取值见表 3,判别结果见表 4.其中d1为粉细砂层顶深度,d2为粉细砂层底深度,ds为标贯深度,dw为地下水位埋深,γu为水位以上土重度,γd为水位以下土重度,ρc为黏粒含量,N为标贯击数,σ0为总上覆压力,ζ为粘粒修正系数,Kh为水平地震系数,Cv为地震剪应力折减系数,Cn为标贯修正系数,σe为有效覆盖压力.
| 表 3 粉细砂液化判别参数 Tab. 3 Liquefaction discrimination parameters of fine sand layer |
从表 4中看出,剪切波速法中Seed法和石兆吉法判别方法与振动台模型试验结果较接近,但石兆吉法对液化层深度的影响考虑不足;而文献[16]和文献[17]的判别结果一致,深度小于10 m、地震动强度≥0.10g时,细粉砂液化;深度≥10 m、地震动强度≥0.15g时,细粉砂液化,说明现行规范中的砂土液化判别方法偏于安全.
| 表 4 不同方法的粉细砂液化判别结果 Tab. 4 Discrimination results of fine sand liquefaction potential by different methods |
由于影响砂土液化的因素十分复杂,在大多数判别方法中往往只考虑其中几项,很难将所有因素全部考虑到,同时这些因素对液化程度的影响、方式还不明确,仍处于试验研究阶段,致使各种判别方法所得结果存在一定的差异,可能会造成误判,因此提出更直观、合理且适用于实际工程的粉细砂液化判别方法十分必要.
4.2 饱和粉细砂液化判别的讨论通过振动台模型试验发现,当地震动强度为0.15g时,模型箱及地基土的反应较小,振动不明显,土层表面渗出少量水,未出现明显喷砂冒水现象,此时深度为5 cm的饱和粉细砂孔压比达到0.8,60、110 cm处孔压比小于0.8;当地震动强度为0.20g时,土层表面渗出大量水,土体有明显的侧向位移,且土层表面出现不均匀沉降,此时饱和粉细砂土层埋置深度5、60 cm处孔压比达到0.8,110 cm处孔压比小于0.8;当地震动强度≥0.25g时,位于地基土表层的饱和粉细砂出现类似流体的运动特征,孔隙水从土体空隙中排出,同时伴有大量气泡冒出,且土层表面出现较明显的不均匀沉降,说明饱和粉细砂完全液化,此时孔压比均≥0.8.因此,将孔压比0.8作为海南铺前大桥桥址区饱和粉细砂液化的临界孔压比,并以孔压比作为饱和粉细砂是否液化的判据之一.按照1/25比尺反推振动台模型试验中粉细砂深度,得到饱和粉细砂液化判别方法见表 5.
| 表 5 饱和粉细砂液化判别表 Tab. 5 Discrimination table for saturated fine sand liquefaction potential |
上述判别方法基于振动台模型试验,以粉细砂深度、地震动强度和孔压比作为粉细砂液化判别标准,拓展了现有液化判别方法的判别标准,较现有常用的液化判别方法更符合工程实际.该方法简便实用,可为今后强震地区的砂土液化判别提供参考.
5 结论1) 通过开展强震作用下饱和粉细砂液化振动台试验,发现饱和粉细砂超静孔隙水压力、孔压比的增长滞后于地震动应力,且在地震波加载完成后,浅层饱和粉细砂孔压比较深层饱和粉细砂达到稳定的时间更短,上覆土层厚度对于饱和粉细砂的抗液化性能起重要影响.
2) 深度为5 cm、60 cm和110 cm的饱和粉细砂,当地震动强度分别≥0.15g、0.20g和0.25g时发生液化,孔压比稳定值均≥0.8,提出海南铺前大桥桥址区饱和粉细砂液化的临界孔压比为0.8.
3) 对比了常用砂土液化判别方法,选用饱和粉细砂深度、地震动强度和孔压比作为饱和粉细砂的液化判据,提出了一种饱和粉细砂液化判别新方法,可为海南铺前大桥及类似工程的砂土液化判别提供参考.
4) 今后需进一步研究地震波类型、土体渗透参数和覆盖层厚度对饱和粉细砂液化特性的影响,以对强震区的砂土液化判别提供理论借鉴.
| [1] |
冯忠居. 特殊地区基础工程[M]. 北京: 人民交通出版社, 2008. FENG Zhongju. Foundation engineering in special areas[M]. Beijing: China Communications Press, 2008. |
| [2] |
王峻, 王兰民, 李兰. 饱和砂土液化的动三轴试验判断与评价[J]. 西北地震学报, 2004, 26(3): 285. WANG Jun, WANG Lanmin, LI Lan. Thedynamic triaxial test discrimination and evaluation for liquefaction of saturated sand[J]. Northwestern Seismological Journal, 2004, 26(3): 285. DOI:10.3969/j.issn.1000-0844.2004.03.017 |
| [3] |
周燕国, 陈云敏, 柯瀚. 砂土液化势剪切波速简化判别法的改进[J]. 岩石力学与工程学报, 2005, 24(13): 2369. ZHOU Yanguo, CHEN Yunmin, KE Han. Improvement of simplified procedure for liquefaction potential evaluation of sands by shear wave velocity[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2369. DOI:10.3321/j.issn:1000-6915.2005.13.028 |
| [4] |
陈国兴, 李方明. 基于径向基函数神经网络模型的砂土液化概率判别方法[J]. 岩土工程学报, 2006, 28(3): 301. CHEN Guoxing, LI Fangming. Probabilistic estimation of sand liquefaction based on neural network model of radial basis function[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 301. DOI:10.3321/j.issn:1000-4548.2006.03.004 |
| [5] |
蔡国军, 刘松玉, 童立元, 等. 基于静力触探测试的国内外砂土液化判别方法[J]. 岩石力学与工程学报, 2008, 27(5): 1019. CAI Guojun, LIU Songyu, TONG Liyuan, et al. Evaluation of liquefaction of sandy soils based on cone penetration test[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(5): 1019. DOI:10.3321/j.issn:1000-6915.2008.05.018 |
| [6] |
金志仁. 基于距离判别分析方法的砂土液化预测模型及应用[J]. 岩土工程学报, 2008, 30(5): 776. JIN Zhiren. Prediction of sand liquefaction based on distance discriminant analysis and its application[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 776. DOI:10.3321/j.issn:1000-4548.2008.05.026 |
| [7] |
颜可珍, 刘能源, 夏唐代. 基于判别分析法的地震砂土液化预测研究[J]. 岩土力学, 2009, 30(7): 2049. YAN Kezhen, LIU Nengyuan, XIA Tangdai. Discriminant analysis model for prediction of sand soil liquefaction during earthquake[J]. Rock and Soil Mechanics, 2009, 30(7): 2049. DOI:10.3969/j.issn.1000-7598.2009.07.030 |
| [8] |
刘勇健. 饱和砂土地震液化判别的可拓聚类预测方法[J]. 岩土力学, 2009, 30(7): 1939. LIU Yongjian. Extension clustering prediction method for evaluation of seismic liquefaction of saturated sandy soil[J]. Rock and Soil Mechanics, 2009, 30(7): 1939. DOI:10.3969/j.issn.1000-7598.2009.07.011 |
| [9] |
曹振中, 袁晓铭. 砂砾土液化的剪切波速判别方法[J]. 岩石力学与工程学报, 2010, 29(5): 943. CAO Zhenzhong, YUAN Xiaoming. Shear wave velocity based approach for evaluating gravel soils liquefaction[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 943. |
| [10] |
刘年平, 王宏图, 袁志刚, 等. 砂土液化预测的Fisher判别模型及应用[J]. 岩土力学, 2012, 33(2): 554. LIU Nianping, WANG Hongtu, YUAN Zhigang, et al. Fisher discriminant analysis model of sand liquefaction and its application[J]. Rock and Soil Mechanics, 2012, 33(2): 554. DOI:10.3969/j.issn.1000-7598.2012.02.036 |
| [11] |
李兆焱, 袁晓铭, 曹振中, 等. 基于新疆巴楚地震调查的砂土液化判别新公式[J]. 岩土工程学报, 2012, 34(3): 483. LI Zhaoyan, YUAN Xiaoming, CAO Zhengzhong, et al. New evaluation formula for sand liquefaction based on survey of Bachu Earthquake in Xinjiang[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(3): 483. |
| [12] |
李兆焱, 王永志, 袁晓铭. 适用于新疆巴楚地区的CPT液化判别新方法[J]. 岩土工程学报, 2013, 35(增刊1): 140. LI Zhaoyan, WANG Yongzhi, YUAN Xiaoming. New CPT-based prediction method for soil liquefaction applicable to Bachu region of Xinjiang[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 140. |
| [13] |
冯忠居, 王溪清, 李孝雄, 等. 强震作用下的砂土液化对桩基力学特性影响[J]. 交通运输工程学报, 2019, 19(1): 71. FENG Zhongju, WANG Xiqing, LI Xiaoxiong, et al. Effect of sand liquefaction on mechanical properties of pile foundation under strong earthquake[J]. Journal of Traffic and Transportation Engineering, 2019, 19(1): 71. DOI:10.3969/j.issn.1671-1637.2019.01.008 |
| [14] |
袁林娟, 刘小生, 汪小刚, 等. 振动台土-箱结构模型动力特性及反应的解析分析[J]. 岩土工程学报, 2012, 34(6): 1038. YUAN LinJuan, LIU Xiaosheng, WANG Xiaogang, et al. Analytic solution of dynamic characteristics and responses of soil-box model for shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1038. |
| [15] |
刘闯, 冯忠居, 张福强, 等. 地震作用下特大型桥梁嵌岩桩基础动力响应[J]. 交通运输工程学报, 2018, 18(4): 53. LIU Chuang, FENG Zhongju, ZHANG Fuqiang, et al. Dynamic response of rock-socketed pile foundation for extra-large bridge under earthquake action[J]. Journal of Traffic and Transportation Engineering, 2018, 18(4): 53. DOI:10.3969/j.issn.1671-1637.2018.04.006 |
| [16] |
中华人民共和国住房和城乡建设部.建筑抗震设计规范: GB 50011—2010[S].北京: 中国建筑工业出版社, 2010 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Construction Industry Press, 2010 |
| [17] |
中华人民共和国交通运输部.公路桥梁抗震设计细则: JTG/T B02-0l—2008[S].北京: 人民交通出版社, 2008. Ministry of Transport of thePeople's Republic of China. Detailed rules for seismic design of highway bridges: JTG/T B02-0l—2008[S]. Beijing: China Communications Press, 2008 |
| [18] |
石兆吉, 郁寿松, 丰万玲. 土壤液化势的剪切波速判别法[J]. 岩土工程学报, 1993, 15(1): 74. SHI Zhaoji, YU Shousong, FENG Wanling. Theshear wave velocity discrimination method for soil liquefaction potential[J]. Journal of Geotechnical Engineering, 1993, 15(1): 74. DOI:10.3321/j.issn:1000-4548.1993.01.011 |
| [19] |
SEED H B, IDRISS I M. Simplified procedure for evaluating soil liquefaction potential[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(9): 1249. |
 2019, Vol. 51
2019, Vol. 51


