由危险货物运输所引起的泄漏事故频繁发生，对人身财产和环境安全造成了重大威胁，相关机构亟需改善危险货物运输安全现状^[1].目前，运输企业普遍采用GPS卫星定位系统对危险货物车辆进行监控，一定程度上提高了运输的安全性.但此类监管只停留在车辆定位追踪层面，并没有基于轨迹数据展开分析，难以清晰地掌握车辆在途活动状态，因而无法及时发现运输过程中存在的问题并采取有效的措施.基于此不足，需要从GPS轨迹数据中识别车辆在途活动类型来提高危险货物运输行业监管水平.

近年来利用GPS数据挖掘交通信息的研究越来越普遍.然而直接从GPS数据中推断活动类型仍面临技术瓶颈.文献[2]直接利用时间间隔来区分活动类型，文献[3]利用GPS数据和辅助随车日志，基于线性SVM算法训练了活动分类器，可以将所有停车事件分为货运停车和非货运停车两类，然而现实中难以获得包含车辆真实活动的辅助信息，活动类型的识别还需依靠无监督学习方法和模型.文献[4]对比了层次聚类和基于划分的聚类方法，选择Ward’s方法来识别重复访问的目的地，以期从活动地点的空间分布特征来推断车辆出行行为.文献[5]则使用基于密度的DBSCAN算法来识别货车锚点，DBSCAN算法比Ward’s方法更能切合GPS数据的空间特性，但是对参数十分敏感.且文献[4-5]只是通过聚类显示了活动节点的空间特征，仅可看作是活动类型识别的前期工作.而文献[6]则利用经纬度乘积生成的识别码对停车事件进行简单聚类，并引入熵的概念提出了基于货车GPS数据的主要停车活动和次要停车活动二分类识别方法.既有研究仅限于解决简单的货运活动和非货运活动二分类问题，没有开展系统的特征体系构建，在缺乏辅助信息的条件下对活动类型的识别准确率低，无法满足精细化监管的需要.

本文针对GPS轨迹数据，除考虑活动的时空特点外，还引入出行链上前后活动类型的相互制约关系，提出一种基于GMM-HMM的多类危险货物运输车辆活动类型识别模型，以期有效提高活动类型识别的精度和实用性，为辅助运输监管决策提供科学依据.

1 数据预处理

在识别危货车辆出行活动类型之前，需预处理所收集的GPS数据，以提取车辆活动节点，并根据其地理空间分布聚类活动热区.

1.1 出行链活动节点提取

令$ S t=\left\{T r_{l} | l=1, 2, \cdots, n_{T}\right\}$为待处理的GPS轨迹数据集，其中n_T为待处理轨迹总数，Tr_l为St中的第l条轨迹，由某辆车某日的GPS轨迹点组成，记作$ T r_{l}=\left\{P_{i}^{l} | i=1, 2, \cdots, n_{P}^{l}\right\}$，其中P_i^l为第l条轨迹中按照时间顺序排列的第i个轨迹点，n_p^l为该轨迹的轨迹点数量.设轨迹点$P_i^l = \left( {x_i^l, y_i^l, d_i^l, t_i^l, s_i^l, h_i^l, e_i^l} \right., \left. {v_i^l, f_i^l} \right) $ ，其中$ x_{i}^{l}, y_{i}^{l}, d_{i}^{l}, t_{i}^{l}, s_{i}^{l}, h_{i}^{l}, e_{i}^{l}, v_{i}^{l}, f_{i}^{l}$分别为该轨迹点的经度、纬度、日期、时间、速度、方位角、引擎状态、车辆编号和首点标记(当i=1时为1，否则为0).由于GPS设备可能会发生定位错误和数据漂移等情况^[7-10]，本文事先对原始GPS数据进行了清洗，以保证数据属性完整、经纬度数据符合研究区域的实际情况，数据的时间属性唯一，数据误差小于规定的阈值.

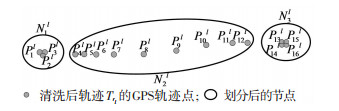
轨迹划分是推断活动节点的前提，本文基于速度变化将轨迹划分为节点.将轨迹Tr_l中速度持续为零的点或持续不为零的点列$ P_\alpha ^l, P_{\alpha + 1}^l, \cdots , P_\beta ^l(1 \le \left. {\alpha \le \beta \le n_P^l} \right)$划分为节点N_j^l，其中α, β分别为构成节点的首末轨迹点的序号.设节点N_j^l的平均速度和持续时间为$ \bar s_j^l, \Delta t_j^l$，则$ {\rm{ }}\bar s_j^l = \sum _{i = \alpha }^\beta {s_i^l} /(\beta - \alpha + 1)$, $\Delta t_{j}^{l}=t_{\beta}^{l}-t_{\alpha}^{l} $.至此轨迹Tr_l可转化为节点序列$ \left\{ {N_j^l|j = } \right.\left. {1, 2, \cdots , n_N^l} \right\}$，其中n_N^l为节点个数.例如，图 1中速度持续为零且坐标相近的点$ P_{1}^{l}, P_{2}^{l}, P_{3}^{l}$被划分为节点$ N_1^l$, 同理$ P_{13}^l - P_{16}^l$划分为节点$N_3^l $.而速度持续不为零的$P_4^l - P_{12}^l $则被抽象成节点N₂^l，节点序列表示为$ \left\{N_{1}^{l}, N_{2}^{l}, N_{3}^{l}\right\}$.

节点序列理论上由行驶节点和活动(停留)节点组成，因此活动节点的识别问题实际上可转化为节点运动状态(停留/行驶)二元分类问题.为了减少主观因素对识别的干预，本文基于决策树算法对节点的运动状态进行判断，步骤如下.

步骤1  当j=1时，初始化节点N₁^l运动状态ms₁^l为“停留”；

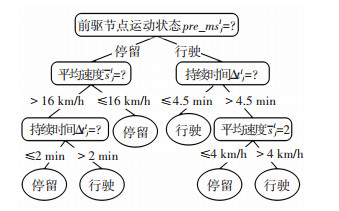
步骤2   当j>1时，根据图 2所示的分类规则依次判断节点的运动状态ms_j^l：对于当前节点N_j^l，设其前驱节点为N_j－1^l，令$ pr{e_ - }ms_j^l$为前驱节点运动状态，有$ p r e_{-} m s_{j}^{l}=m s_{j-1}^{l}$；将$ {N_j^l}$的平均速度、持续时间和前驱节点的运动状态输入到图 2的规则中，输出该节点运动状态的判断结果.

步骤3  将$ms_j^l $为“停留”的节点${N_j^l} $提取为活动节点$ A_k^l$，此时$A_{k}^{l}=N_{j}^{l}=\left\{P_{\alpha}^{l}, P_{\alpha+1}^{l}, \cdots, P_{\beta}^{l}\right\} $.轨迹Tr_l上的所有活动节点组成第l条出行链活动序列$C h_{l}=\left\{A_{k}^{l} | k=1, 2, \cdots, n_{A}^{l}\right\} $，其中$ {n_A^l}$为出行链l中活动节点个数.

1.2 活动热区识别

按照1.1的方法，处理所有的GPS轨迹，并将提取出的各条出行链的活动节点添加到同一个集合Ac中，即$A c=\left\{A_{k}^{l} | l=1, 2, \cdots, n_{T} ; k=1, 2, \cdots, n_{A}^{l}\right\} $.

在提取群体特征之前，需将所有活动节点按照地理空间坐标聚类为活动热区.文献[5]表明基于密度的聚类算法因其抗噪声能力强，能发现任意形状的簇等优点，在空间数据的聚类分析中比其他聚类方法更适用. OPTICS^[11]是最具代表性的基于密度的聚类算法之一，它克服了文献[5]提到的DBSCAN算法使用全局密度易丢失簇的缺点，可以通过点排序来识别变密度聚类结构.本文基于经典OPTICS算法, 引入随机退出技术(Dropout)，设计了D-OPTICS算法对活动热区进行识别，该算法在继承OPTICS算法优点的同时，解决了OPTICS存在的两大问题.

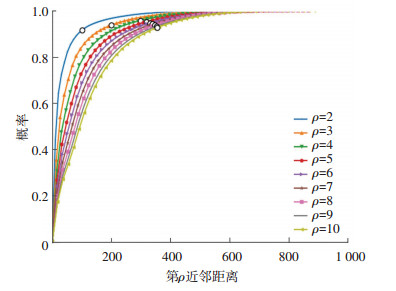
1) 最优参数确定.为确保大多数活动节点被有效聚类，在D-OPTICS中，根据活动节点数据集Ac的统计特性选择关键参数ρ(形成团簇所需的最小点数)和ε(邻域半径)的值.依次令ρ=2, 3, …, 10，对于任意活动节点$ A_{k}^{l} \in A c$，计算出与$ A_k^l$第ρ近的对象距离${{d_\rho }\left( {A_k^l} \right)} $，遍历Ac得到集合$ D_{\rho}=\left\{d_{\rho}\left(A_{k}^{l}\right)\right\}$，对D_ρ排序并绘制累积概率分布图，如图 3所示，第ρ近邻距离累积概率分布曲线均是先急剧上升后趋于平缓的曲线.将转折点(图 3中空心点)的横坐标值记为ε，计算对应于该参数组合(ρ, ε)的Ac数据集噪声比例.取噪声比例最小时对应的参数组合作为最优参数取值^[12].

2) 避免过度聚类：D-OPTICS算法中引入随机退出技术，使OPTICS有序队列中的扩展点具有随机不可连接性，可防止过度聚类，并利用高斯混合聚类对结果进行二次优化.

采用D-OPTICS对Ac中的活动节点进行聚类，得到的“类簇”即为活动热区，可表示为H_u，设$ {H_u} = \left( {{\mathop{\rm avg}\nolimits} {T_u}, {\mathop{\rm avg}\nolimits} {F_u}, E{n_u}} \right)$，其中${{\mathop{\rm avg}\nolimits} {T_u}, {\mathop{\rm avg}\nolimits} {F_u}, E{n_u}} $分别为该热区的平均活动持续时间、平均首点率和熵指数.若热区H_u包含活动节点$A_k^l $，则$A_k^l $的所属热区编号ID_k^l=u.

2 多尺度特征体系构建 2.1 多尺度特征

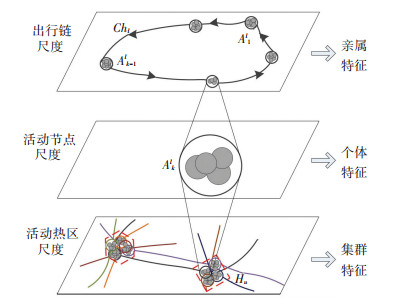
获取适合活动类型识别任务的有效特征，对正确揭示活动本质十分关键.为了防止特征缺陷所可能导致的偏颇、歪曲、有缺陷的识别结论，需要尽可能完整且层次丰富地构建相关特征^[13].遵循此原则，本文从活动节点自身、节点所处出行链以及节点所在热区3个尺度构建了个体特征、亲属特征和集群特征，图 4展示了不同尺度下所提取的特征种类以及尺度间的关系.

个体特征指的是当前所关注的活动节点$A_k^l $的个体属性，包括：所含轨迹点数F1_k^l、活动开始时间F2_k^l、持续时长F3_k^l、结束时间F4_k^l、轨迹点间平均时间间隔F5_k^l、首末轨迹点距离F6_k^l、轨迹点总移动里程F7_k^l、轨迹点间平均距离F8_k^l、迂回系数F9_k^l、经纬度标准差F10_k^l和F11_k^l、各轨迹点与活动节点中心的平均距离F12_k^l、最远距离F13_k^l; 活动节点的经纬距离F14_k^l和F15_k^l、长宽比F16_k^l、面积F17_k^l、点密度F18_k^l; 首末轨迹点方位角之差的绝对值F19_k^l、方位角改变次数F20_k^l、方位角改变度数均值F21_k^l; 平均速度F22_k^l、速度增减趋势改变次数F23_k^l; 首末轨迹点引擎状态F24_k^l和F25_k^l、引擎状态均值F26_k^l、引擎状态改变次数F27_k^l、引擎状态为熄火的轨迹点数F28_k^l.则有

$ F1_k^l = \beta - \alpha + 1, $

(1)

$ F2_k^l = t_\alpha ^l, $

(2)

$ F3_k^l = t_\beta ^l - t_\alpha ^l, $

(3)

$ F4_k^l = F2_k^l + F3_k^l, $

(4)

$ F5_k^l = F3_k^l/\left( {\beta - \alpha } \right), $

(5)

$ F6_k^l = {\rm{dist}}\left( {\left[ {x_\alpha ^l,y_\alpha ^l} \right],\left[ {x_\beta ^l,y_\beta ^l} \right]} \right), $

(6)

$ F7_k^l = \sum\nolimits_{i = \alpha + 1}^\beta {{\rm{dist}}\left( {\left[ {x_{i - 1}^l,y_{i - 1}^l} \right],\left[ {x_i^l,y_i^l} \right]} \right)} , $

(7)

$ F8_k^l = F7_k^l/\left( {\beta - \alpha } \right), $

(8)

$ F9_k^l = F7_k^l/F6_k^l, $

(9)

$ F10_k^l = \sqrt {\sum\nolimits_{i = \alpha }^\beta {{{\left( {x_i^l - \bar x_k^l} \right)}^2}/\left( {\beta - \alpha + 1} \right)} } , $

(10)

$ F11_k^l = \sqrt {\sum\nolimits_{i = \alpha }^\beta {{{\left( {y_i^l - \bar y_k^l} \right)}^2}/\left( {\beta - \alpha + 1} \right)} } , $

(11)

$ F12_k^l = \sum\nolimits_{i = \alpha + 1}^\beta {{\rm{dist}}\left( {\left[ {\bar x_k^l,\bar y_k^l} \right],\left[ {x_i^l,y_i^l} \right]} \right)} /\left( {\beta - \alpha + 1} \right), $

(12)

$ F13_k^l = \mathop {\max }\limits_{\alpha \le i \le \beta } \left( {{\rm{dist}}\left( {\left[ {\bar x_k^l,\bar y_k^l} \right],\left[ {x_i^l,y_i^l} \right]} \right)} \right), $

(13)

$ F14_k^l = \mathop {\max }\limits_{\alpha \le i \le \beta } \left( {x_i^l} \right) - \mathop {\min }\limits_{\alpha \le i \le \beta } \left( {x_i^l} \right), $

(14)

$ F15_k^l = \mathop {\max }\limits_{\alpha \le i \le \beta } \left( {y_i^l} \right) - \mathop {\min }\limits_{\alpha \le i \le \beta } \left( {y_i^l} \right), $

(15)

$ F16_k^l = \max \left( {F14_k^l/F15_k^l,F15_k^l/F14_k^l} \right), $

(16)

$ F17_k^l = F14_k^l \times F15_k^l, $

(17)

$ F18_k^l = F1_k^l/F17_k^l, $

(18)

$ F19_k^l = \min \left( {360 - \left| {h_\alpha ^l - h_\beta ^l} \right|,\left| {h_\alpha ^l - h_\beta ^l} \right|} \right), $

(19)

$ F20_k^l = \sum\nolimits_{i = \alpha + 1}^\beta {\left( {\max \left( {\left| {h_i^l - h_{i - 1}^l} \right|,0} \right)/\left| {h_i^l - h_{i - 1}^l} \right|} \right)} , $

(20)

$ F21_k^l = F19_k^l/F20_k^l, $

(21)

$ F22_k^l = \sum\nolimits_{i = \alpha }^\beta {s_i^l/\left( {\beta - \alpha + 1} \right)} , $

(22)

$ F23_k^l = \sum\nolimits_{i = \alpha + 1}^\beta {\frac{{\min \left( {\left( {s_i^l - s_{i - 1}^l} \right) \times \left( {s_{i - 1}^l - s_{i - 2}^l} \right),0} \right)}}{{\left( {s_i^l - s_{i - 1}^l} \right) \times \left( {s_{i - 1}^l - s_{i - 2}^l} \right)}}} , $

(23)

$ F24_k^l = e_\alpha ^l, $

(24)

$ F25_k^l = e_\beta ^l, $

(25)

$ F26_k^l = \sum\nolimits_{i = \alpha }^\beta {e_i^l/\left( {\beta - \alpha + 1} \right)} , $

(26)

$ F27_k^l = \sum\nolimits_{i = \alpha + 1}^\beta {\left( {\max \left( {\left| {e_i^l - e_{i - 1}^l} \right|,0} \right)/\left| {e_i^l - e_{i - 1}^l} \right|} \right)} , $

(27)

$ F28_k^l = \sum\nolimits_{i = \alpha }^\beta {\max \left( {e_i^l - 4,0} \right)} . $

(28)

式中α、β分别为构成活动节点$A_k^l $的首、末轨迹点在第l条轨迹上的序号；$ x_{i}^{l}、y_{i}^{l}、t_{i}^{l}、s_{i}^{l}、h_{i}^{l}、e_{i}^{l}$分别为第l条轨迹中第i个轨迹点的经度、纬度、时间、速度、方位角和引擎状态，而$ x_{\alpha}^{l}、y_{\alpha}^{l}、t_{\alpha}^{l}、s_{\alpha}^{l}、h_{\alpha}^{l}、e_{\alpha}^{l}$和$ x_\beta ^l、y_\beta ^l、t_\beta ^ls_\beta ^l、h_\beta ^l、e_\beta ^l$分别为i=α和i=β时对应的属性取值；$ \bar{x}_{k}^{l}、\bar{y}_{k}^{l}$分别为$A_k^l $的中心经、纬度；dist、max、min、||分别为求距离、最大值、最小值、绝对值的函数；

亲属特征围绕当前活动节点$A_k^l $在相应出行链活动序列Ch_l上所处的时空位置特点而展开，包括$A_k^l $所在物理位置的当日访问次数F29_k^l，A_k^l与前一活动节点A_k－1^l的时空距离F30_k^l和F31_k^l，A_k^l与当日出行链起点A₁^l的时空距离F32_k^l和F33_k^l.

$ F29_k^l = \sum\limits_{p = 1}^{n_A^l} {\frac{{\min \left( {{\rm{dist}}\left( {\left[ {\bar x_x^l,\bar y_p^l} \right],\left[ {\bar x_k^l,\bar y_k^l} \right]} \right) - 50,0} \right)}}{{{\rm{dist}}\left( {\left[ {\bar x_p^l,\bar y_p^l} \right],\left[ {\bar x_k^l,\bar y_k^l} \right]} \right) - 50}}} , $

(29)

$ F30_k^l = F2_k^l - F2_{k - 1}^l\left( {k > 1} \right);F30_k^l = 0\left( {k = 1} \right). $

(30)

$ F31_k^l = \left\{ {\begin{array}{*{20}{l}} {{\rm{dist}}\left( {\left[ {\bar x_k^l,\bar y_k^l} \right],\left[ {\bar x_{k - 1}^l,\bar y_{k - 1}^l} \right]} \right),}&{k > 1;}\\ {0,}&{k = 1.} \end{array}} \right. $

(31)

$ F32_k^l = F2_k^l - F2_1^l, $

(32)

$ F33_k^l = {\rm{dist}}\left( {\left[ {\bar x_k^l,\bar y_k^l} \right],\left[ {\bar x_1^l,\bar y_1^l} \right]} \right). $

(33)

式中$\bar{x}_{p}^{l}、\bar{y}_{p}^{l} $分别为$A_k^l $在同一出行链上的第p个活动节点的中心经、纬度.

集群特征刻画的是与$A_k^l $处于同一热区H_u内的所有活动节点所呈现的共性特征，提取为所在热区的平均活动持续时间F34_k^l、平均起点包含率F35_k^l和混合熵指数F36_k^l.

$ F34_k^l = {\rm{avg}}{T_u}, $

(34)

$ F35_k^l = {\rm{avg}}{F_u}, $

(35)

$ \begin{array}{l} F36_k^l = E{n_u} = \\ \;\;\; - \left( {\sum\limits_{c = 1}^C {\left( {\left( {\frac{{n_c^u}}{{n_A^u}}} \right)\ln \left( {\frac{{n_c^u}}{{n_A^u}}} \right)} \right)} + \sum\limits_{g = 1}^G {\left( {\left( {\frac{{n_g^u}}{{n_A^u}}} \right)\ln \left( {\frac{{n_g^u}}{{n_A^u}}} \right)} \right)} } \right). \end{array} $

(36)

式中n_A^u为热区H_u所含活动节点总数，n_c^u为运营商c的车辆在该热区内产生的活动节点数，C为在该热区停留车辆涉及的运营商总数，n_g^u为在该热区运输g类货物的活动节点数，G为该热区运输的所有货物种类数.

2.2 特征降维

为减少原始多维特征空间中冗余信息所造成的误差，需要对数据进行降维.考虑到所用的数据缺乏标签，选用无监督降维方法.主成分分析(PCA)和因子分析(FA)是目前最常用的无监督降维方法，本文比较了分别使用PCA和FA方法将数据降到不同维度时的平均对数似然得分，对数似然值越大，表明效果越好.由图 5可知，随着维数的增加，两种方法的对数似然值均逐渐上升，但FA的降维效果始终优于PCA；且降维到20维时，FA的得分已接近收敛.因此选用FA方法变换得到的20维特征向量作为后续模型的特征输入.

3 活动类型识别 3.1 模型选择

隐马尔科夫模型(HMM)^[14]作为序列数据处理和统计学习的一种重要概率模型，具有建模简单，物理意义明确等优点.考虑到所构建的特征为多维连续特征，可假定每维特征均服从混合高斯分布.因此本文选用基于混合高斯模型的隐马尔科夫模型(GMM-HMM)识别车辆出行链的活动类型.

识别模型定义如下：所有可能的活动类型集合为$ S=\left\{S_{1}, S_{2}, \cdots, S_{N}\right\}$，初始活动类型的概率向量为$ \pi=\left(\pi_{i}\right), i=1, 2, \cdots, N, N$为可能的活动类型数，$ \pi_{i}=P\left(i_{1}=S_{i}\right)$；状态转移概率矩阵$a_{i j}=P\left(i_{k+1}=S_{j} | i_{k}=S_{i}\right), i=1, 2, \cdots, N ; j=1, 2, \cdots $；π和A决定出行链活动序列Ch_l内各活动的类型，记为活动类型序列$ I q=\left(i_{1}, \cdots, i_{k}, \cdots, i_{n_{A}}\right), n_{A}$为待观测活动个数；各活动类型对应的可观测特征序列为$O q=\left(o_{1}, \cdots, o_{k}, \cdots, o_{n_{A}}\right) $，由观测概率矩阵B来决定，且$o_{k}=\left(F_{1}, F_{2}, \cdots, F_{n_{F}}\right)^{\mathrm{T}} $，其中F为可观测特征变量，n_F为特征变量个数，根据降维结果取n_F= 20；特别地，因本研究中提取的特征变量是连续值，B无法用常规矩阵的形式表示，因此以混合高斯模型(GMM)来拟合B，即令$\mathit{\boldsymbol{B}} = {\left[ {{b_j}(\mathit{\boldsymbol{o}})} \right]_{n \times 1}}, {b_j}(\mathit{\boldsymbol{o}}) = \mathit{\Sigma} _{m = 1}^M{\omega _{jm}}{b_{jm}}(o) = \mathit{\Sigma} _{m = 1}^M{\omega _{jm}}{(2\pi )^{ - {n_F}/2}}{\rm{|}}\sum\nolimits_{jm} {} | ^{- 0.5}$ $ \times \exp \left\{ { - 0.5{{\left( {o - {\mu _{jm}}} \right)}^{\rm{T}}}\mathit{\Sigma} _{jm}^{ - 1}\left( {o - {\mu _{jm}}} \right)} \right\} $，其中o为特征向量可取的一组数值，ω_jm为混合系数，M为高斯个数，Σ_jm为协方差矩阵，$|\sum\nolimits_{jm} | $为协方差行列式，μ_jm为特征均值向量，${{{\left( {o - {\mu _{jm}}} \right)}^{\rm{T}}}} $为$ {\left( {o - {\mu _{jm}}} \right)}$的转置；将B输入到连续HMM模型中，最终建立的GMM-HMM模型为λ=(π, A, B).

3.2 参数估计

Baum-Welch算法是一种广泛使用的方法来估计HMM的参数，算法步骤如下.

步骤1   初始化GMM-HMM模型参数.对于活动识别模型，参数的初值设定尤为重要，因为危险货物运输过程涉及的车辆车型复杂，承载的介质种类繁多，不同的运输出行链无法共享相同的初始参数矩阵.本研究提出了如下HMM模型初始化思路：

1) 采用岭回归方法初始化参数π和A：以调查收集的带活动类型标签的小规模出行链数据作为训练集，为每条出行链提取V维属性向量$ \mathit{\boldsymbol{Z}} = {\left( {{z_1}, {z_2}, \cdots , {z_V}} \right)^{\rm{T}}}$，如出行链长度、总耗时、活动总时长等；用岭回归方法训练一个带有系数矩阵w的线性模型来表征出行链属性和HMM参数(π, A)之间的关系；对于活动类型未知且属性矩阵为${\mathit{\boldsymbol{\hat Z}}} $的任一出行链，则可按照系数矩阵w预测得到参数(π, A)的初始值$ \left( {{\pi ^{(0)}}, {\mathit{\boldsymbol{A}}^{(0)}}} \right) = \mathit{\boldsymbol{\hat Z}}w$.

2) 采用K-Means聚类^[15]方法将训练集中的数据分为N类，计算均值及协方差矩阵以初始化参数B，记作B⁽⁰⁾.至此，模型参数可初始化为$ {\lambda ^{(0)}} = \left( {{\pi ^{(0)}}, {\mathit{\boldsymbol{A}}^{(0)}}, {\mathit{\boldsymbol{B}}^{(0)}}} \right)$，令n=0开始迭代.

步骤2   利用EM算法迭代学习参数.根据当前参数估计值λ⁽ⁿ⁾计算Q函数：

$ \begin{array}{l} Q\left( {\lambda ,{\lambda ^{(n)}}} \right) = \sum\limits_{Iq} {\log {{\rm{ \mathsf{ π} }}_{{i_1}}}P\left( {Oq,Iq|{\lambda ^{(n)}}} \right)} + \\ \;\;\;\;\;\;\sum\limits_{Iq} {\left( {\sum\limits_{k = 1}^{{n_A}} {\log } {a_{{i_k}\;\;{i_{k + 1}}}}} \right)} P\left( {Oq,Iq|{\lambda ^{(n)}}} \right) + \\ \;\;\;\;\;\;\sum\limits_{Iq} {\left( {\sum\limits_{k = 1}^{{n_A}} {\log {b_{{i_k}}}\left( {{o_k}} \right)} } \right)} P\left( {Oq,Iq|{\lambda ^{(n)}}} \right). \end{array} $

(37)

然后分别极大化式(37)的各项，以确定模型参数的新估计值${\lambda ^{(n + 1)}} = \mathop {\arg \max }\limits_\lambda Q\left( {\lambda , {\lambda ^{(n)}}} \right) $.

步骤3   重复步骤2，直到收敛，得到模型参数$ {\lambda ^{(n + 1)}} = \left( {{\pi ^{(n + 1)}}, {\mathit{\boldsymbol{A}}^{(n + 1)}}, {\mathit{\boldsymbol{B}}^{(n + 1)}}} \right)$.

3.3 活动解码

在学习好的参数基础上，使用Viterbi算法求取最佳活动类型序列.维特比算法实际是用动态规划求概率最大的出行链活动类型序列.定义第k个活动的类型为S_i观测到特征o_k的概率为δ_k(i)，使δ_k(i)最大的第k－1个活动的类型为ψ_k(i).步骤如下：当k=1时，初始化$ \delta_{1}(i)=\pi_{i} b_{i}\left(o_{1}\right), \psi_{1}(i)=0$，其中i=1, 2, …, N；对k=2, 3, …, n_A，依次令${\delta _k}(i) = \mathop {\max }\limits_{1 \le j \le N} \left[ {{\delta _{k - 1}}(j){a_{ij}}} \right]{b_i}\left( {{o_k}} \right), {\psi _k}(i) = \arg \mathop {\max }\limits_{1 \le j \le N} \left[ {{\delta _{k - 1}}(j){a_{ji}}} \right] $；最终$i_{{n_A}}^* = \arg \mathop {\max }\limits_{1 \le j \le N} {\delta _{{n_A}}}(i) $，回溯最优路径，可知对$ k = {n_A} - 1, {n_A} - 2, \cdots , 1$，有$ i_k^* = {\psi _{k + 1}}\left( {i_{k + 1}^*} \right)$，求得最优活动类型序列为：$I q^{*}=\left(i_{1}^{*}, i_{2}^{*}, \cdots, i_{n_{A}}^{*}\right) $.

4 实验结果和分析

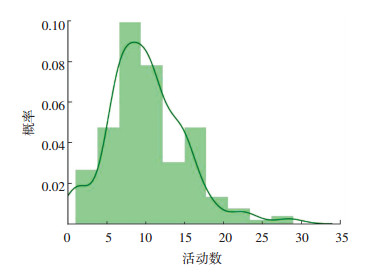
本文获取了2015年11月1日至11月7日期间，属于108家企业共计1115辆危险品车辆的大规模GPS数据，约有400万条记录.另外还收集了相应车辆的属性数据，这些车辆的可搭载介质主要涉及第1、2、3、4、6、8类危险货物，代表爆炸品、压缩气体、易燃液体、易燃固体、有毒物质和腐蚀品^[16].按照第1节的方法预处理GPS数据，最终识别出26 176个活动节点，聚类得到1 609个活动热区，形成了3 358条出行链.出行链活动数的概率分布如图 6，日均活动数为8.6个.为了更好地初始化GMM- HMM模型参数，调查了其中的182条出行链数据的真实活动类型标签(称为小规模数据).调查可知出行链包含装载(L)、卸载(U)、归场(Y)、交通堵塞(J)、信号灯等待(T)、途中休息(R)、夜间住宿(H)、手续办理(O)和其他(E)九类活动.

利用式(1)~(36)，对26 176个活动节点进行多尺度特征构建，并用FA方法降维得到20维特征向量.设HMM模型的隐藏状态数N=9，在活动类型识别之前，先用第3.1节方法，以60%的小规模出行链数据初始化模型参数.在此基础上，为大规模数据集中的每条出行链训练一个GMM-HMM模型推测活动序列，最终识别出所有出行链上活动节点的类型.

由于缺少大规模出行链数据的真实活动信息，因此本文一方面使用剩余40%的小规模出行链数据的真实活动标签来评估活动识别准确性；另一方面，利用POI信息间接评估大规模活动的识别效果.

4.1 直接评估

利用式(38)所定义的评估指标F1分值来直接度量危险货物运输车辆的活动类型识别模型在小规模样本集上的性能，F1是对召回率γ和精确率σ的折中.一般来说，F1分值越高，认为识别率越高.

$ F1 = 2\left( {\sigma \times \gamma } \right)/\left( {\sigma + \gamma } \right). $

(38)

对于单类活动${S_j} \in \{ L, U, \cdots , E\} , {\gamma _j} = T{P_j}/\left( {T{P_j} + } \right.\left. {F{N_j}} \right), {\sigma _j} = T{P_j}/\left( {T{P_j} + F{P_j}} \right) $，其中TP_j, FN_j分别为活动类型S_j被正确识别和被错误识别的数量；FP_j为其他活动类型被错误识别为S_j的数量；而对于整体活动类型(ALL)，$ {\gamma _{{\rm{ALL}}}} = \sum\nolimits_{j = 1}^N {} {w_j} \cdot {\gamma _j}, {\sigma _{{\rm{ALL}}}} = \sum\nolimits_{j = 1}^N {} {w_j} \cdot {\sigma _j}$，其中w_j为活动类型S_j在所有活动的样本占比.

对比调查所得的小规模真实活动数据与本文方法得到的活动类型识别结果，计算本文方法的性能对单一活动和整体活动的识别性能，结果见表 1.从表 1可以看出，本文方法对危险货物运输车辆不同类别活动的识别表现差异较大，F1分值最小低至0.48，最大可达0.88，识别错误偏向于样本占比较少的类别，存在类别不均衡现象：

一方面，装载(L)、卸载(U)、归场(Y)等货运相关活动类型的F1分值普遍高于非货运活动类型(J、T、R、H、O、E)的F1分值，这是因为货车出行主要是为了开展货运相关活动，此类活动发生频繁、特点突出，因此数据样本丰富且彼此的特征差异明显，识别效果较好；而另一方面，针对非货运相关活动，对信号灯等待(T)和手续办理(O)活动的识别效果良好；而对交通堵塞(J)和途中休息(R)、夜间住宿(H)和其他(E)活动识别效果不佳.这是由于这些活动在运输途中不常发生，数据样本占比太小，导致所包含的特征过少，很难从中提取规律，活动类型无法被正确识别.

解决样本分布不均衡问题主要是通过某一途径来使不同类别的样本数据记录均衡.如果条件支持，扩充小类数据集是最简单且高效的方法^[17].进一步分析可知，识别效果较差的4类活动J、R、H、E更容易产生于长途运输过程中.因此为了提高这四种活动类型的样本量，添加长途运输车辆的出行链数据至小规模活动数据集来优化样本分布.优化前后的识别效果指标对比见表 2，调整样本分布后本文方法对各类活动的识别性能有所提升，识别效果稳定；且对所有活动类型的总体识别效果度量指标F1分值由原来0.77提高到了0.84，换言之，活动识别率超过80%.

4.2 间接评估

兴趣点(POI)数据库通常可以从开源地图或商业API中获得，由于POI数据描述的是地点周围的POI类别标签，可以反映地点和潜在的活动类型之间的相关性^[18]，因此研究利用从百度地图API爬取的POI数据来间接验证本文方法对大规模出行链活动的识别效果，具体步骤如下：

首先设定9种活动类型对应的POI类别名称:活动类型是L/U/Y时，对应的POI类别可为公司企业、加油站(3类适用)、加气站(2类适用)、餐饮(2类适用)、医疗和科研机构(2、8类适用)；当活动类型为J/T时，POI类别为交通设施；当活动类型为R、H时，POI类别分别对应于餐饮、服务区；而活动类型为O，POI类别为公司企业或政府机构；活动类型为E时，POI类别应为汽车服务或加油站(3类除外).使用本文方法对大规模出行链节点的活动类型进行识别，并为每一节点的活动类型识别结果匹配潜在POI类别名称.然后根据经纬度信息为每一活动节点匹配其50米范围内从百度地图API爬取到的所有POI类别中标记出现次数最多POI类别名称.若潜在POI类别名称与出现次数最多POI名称的交集不为空，则认为该节点的活动类型被成功识别.对于大规模出行链数据，活动识别率定义为活动类型被成功识别的节点数占出行链总节点数的百分比，最终间接验证结果表明本方法可有效识别出大规模出行链数据中的活动类型，活动识别率(89.1%)在80%以上.

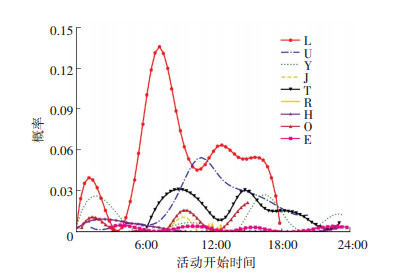
对识别出的各类活动开始时间进行分析，如图 7所示，“装载(L)”活动的典型开始时间呈现多峰值，分别在凌晨、上午和下午；“卸载(U)”的开始时间多数处于午后，峰值接近中午时分；“归场(Y)”活动有明显早出晚归的规律；“交通堵塞(J)”则主要发生于早高峰时段；白天全天均存在“信号灯等待(T)”；“途中休息(R)”集中于午间时段；“夜间住宿(H)”多数开始于午夜或是凌晨；“手续办理(O)”的开始时间与货运活动(L、U、Y)的开始时间关系密切；而“其他(E)”活动开始时间比较分散.上述开始时间的分布符合实际情况，因此本文方法的识别结果可靠性高，可以进一步服务于运输安全监管工作.

5 结论

1) 对危险货物运输车辆的GPS数据应用决策树起停分类模型提取出行链活动节点，设计D-OPTICS算法将活动节点快速聚类生成活动热区；根据个体、亲属和群体多尺度进行特征体系构建，充分考虑了车辆活动的时空特点.在此基础上，应用GMM-HMM模型以超过80%的识别率区分九类车辆活动.

2) 不同于以前研究中货运/非货运活动的两类识别结果，多类识别结果可用于确定车辆在途装载状态，分析货运表现，识别异常活动等研究中，对于促进危险货物运输安全有较强指导意义.下一步研究可从以下两方面着手：基于GMM-HMM的活动类型识别方法的识别率与HMM模型的初始参数关系密切，需要进一步收集样本，优化参数矩阵，从而避免过拟合；还需结合轨迹模式挖掘技术对各类活动的规律进行深入剖析.