机动飞行指飞机飞行状态随时间改变的飞行动作,是对航空发动机性能评价的重要指标[1].机动飞行状态会将附加的激励力即机动载荷引入到航空发动机转子系统中,并改变转子系统的非线性动力学状态.在某些参数下,可能造成系统的严重失稳,对航空发动机的安全运行造成严重威胁.此外,系统实际工作过程中,轴承的刚度特性是受转子运动状态影响而不断改变的,同时转子运动状态也会受轴承刚度变化的影响而发生变化.含碰摩故障的航空发动机在机动飞行状态下高转速运行时尤其如此,碰摩故障、轴承与转子系统相互耦合,使系统表现出强烈的非线性行为.
一直以来,高速滚动轴承-转子系统的研究都是学者们关注的热点. Harsha等[2]建立了考虑轴承径向间隙及滚道表面波纹度等因素的深沟球轴承-高速转子分析模型. Liew等[3]基于Hertz理论对齿轮系统中滚动轴承刚度的时变特征进行了分析计算. Petersen等[4]提出了一个考虑变载荷和时变刚度的滚动轴承模型,并对轴承含缺陷时的刚度变化进行了计算和分析.曹宏瑞等[5]建立了考虑离心力、陀螺力矩、轴承内圈离心膨胀和热变形的高速滚动轴承模型,并计算了轴承的时变刚度. Cao等[6]提出了一种新的基于刚性元件的滚动轴承-转子系统动态建模方法并进行了实验验证. Wu等[7]利用力与变形的关系建立了圆锥滚子轴承弯曲刚度的计算模型,并采用传递矩阵法研究了轴承变形对转子系统的影响.
Batailly等[8]利用模态坐标转换法将离散后的高自由度方程简化为低自由度的方程,基于拉格朗日乘子法研究了叶片和机匣间的碰摩问题. Groll等[9]提出了一种数值方法,求解了碰摩转子系统周期解及其稳定性,基于谐波平衡的思想,分析了系统的分岔行为.陈果等[10]建立了考虑叶片数和动态转静间隙的碰摩模型,并对模型的碰摩特性进行了研究. Ma等[11]分析了碰摩与裂纹故障耦合动力学及碰摩与油膜失稳故障耦合动力学.
杨永锋等[12-13]研究了机动飞行作用下的考虑裂纹因素的刚性支撑转子系统的非线性动力学响应.但对机动飞行的研究所建立的模型为简单平面运动,对于空间复杂飞行运动没有给出机动载荷的推导.祝长生等[14-15]利用拉格朗日方程建立了飞机在做任意机动飞行时多盘转子系统运动微分方程,用数值方法研究了飞机在水平盘旋、俯冲拉起和横滚机动飞行对转子系统的动力学影响.但是仅考虑了线性支承,忽略了大量非线性因素对系统的影响. Hou等[16-17]建立了滚动轴承支承下的转子系统在机动飞行条件下的动力学微分方程,并且考虑了碰摩及裂纹等故障,利用数值法研究了机动载荷对系统的非线性动力学影响.
为建立更符合实际工况的轴承-转子系统模型,考虑滚动轴承时变刚度与转子非线性动力学特性之间的相互影响,本文建立了爬升-俯冲机动飞行状态下含滚动轴承时变刚度的轴承-碰摩转子系统模型,讨论了轴承刚度的时变规律与转子动态特性间的相互关系,研究了机动载荷对系统非线性动力学特性的影响,并分析了含碰摩刚度的变刚度轴承-转子系统非线性动力学特性.
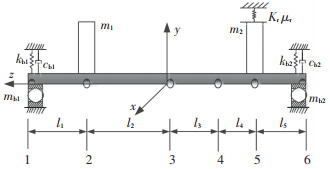
1 系统模型 1.1 机动飞行状态下轴承-转子系统模型图 1为变刚度轴承-碰摩转子系统有限元模型结构图.模型考虑了节点位移对轴承支承刚度kb1与kb2的动态影响,同时考虑在节点5处发生单点碰摩.此外,模型考虑转子偏心及滚动轴承径向间隙的影响.
|
节点1、6—高速滚动轴承;节点2、5—集中质量圆盘;m1、m2—转盘1、2的集中质量; mb1、mb2—左、右支撑轴承的集中质量;e1、e2—转盘1和2的偏心距;Jdi、Jpi(i=1, 2)—转盘1和2的直径转动惯量和极转动惯量;kb1、kb2—左、右支撑轴承的刚度;cb1、cb2—左、右轴承外圈与轴承座的连接阻尼,Kr—碰摩刚度;μr—摩擦因数 图 1 转子-滚动轴承系统模型 Fig. 1 Rotor-bearing system model |
根据Lagrange方程,对转子系统单元轴段的动力学微分方程进行推导:
| $ \begin{array}{l} m\ddot y + k\left( {2y + {l_1}{\theta _x} - {l_2}{\theta _x}} \right) + \alpha \left[ {{{\left( {y + {l_1}{\theta _x}} \right)}^2} + } \right.\\ \left. {{{\left( {x - {l_1}{\theta _y}} \right)}^2}} \right]\left( {y + {l_1}{\theta _x}} \right) + \alpha \left[ {{{\left( {y - {l_2}{\theta _x}} \right)}^2} + } \right.\\ \left. {{{\left( {x + {l_2}{\theta _y}} \right)}^2}} \right]\left( {y - {l_2}{\theta _x}} \right) + c\left( {2\dot y + {l_1}{{\dot \theta }_x} - {l_2}{{\dot \theta }_x}} \right) = \\ m{\omega ^2}e\cos \omega t + m\left( {\omega _x^2 + \omega _z^2} \right)y - m\left( {{\omega _y}{\omega _x} - {{\dot \omega }_z}} \right)x + \\ 2m{\omega _z}\dot x - m\left( {{{\ddot y}_{\rm{F}}} + {\omega _x}{{\dot z}_{\rm{F}}} - {\omega _z}{{\dot x}_{\rm{F}}} + {\omega _z}{\omega _y}z + {{\dot \omega }_x}z} \right), \end{array} $ | (1) |
| $ \begin{array}{l} m\ddot x + k\left( {2x - {l_1}{\theta _y} - {l_2}{\theta _y}} \right) + \alpha \left[ {{{\left( {y + {l_1}{\theta _x}} \right)}^2} + } \right.\\ \left. {{{\left( {x - {l_1}{\theta _y}} \right)}^2}} \right]\left( {x - {l_1}{\theta _y}} \right) + \alpha \left[ {{{\left( {y - {l_2}{\theta _x}} \right)}^2} + } \right.\\ \left. {{{\left( {x + {l_2}{\theta _y}} \right)}^2}} \right]\left( {x + {l_2}{\theta _y}} \right) + c\left( {2\dot x - {l_1}{{\dot \theta }_y} - {l_2}{{\dot \theta }_y}} \right) = \\ m{\omega ^2}e\sin \omega t + m\left( {\omega _z^2 + \omega _y^2} \right)x - m\left( {{\omega _y}{\omega _x} + {{\dot \omega }_z}} \right)y + \\ 2m{\omega _z}\dot y - m\left( {{{\ddot x}_{\rm{F}}} - {\omega _y}{{\dot z}_{\rm{F}}} + {\omega _z}{{\dot y}_{\rm{F}}} + {\omega _x}{\omega _z}z - {{\dot \omega }_y}z} \right), \end{array} $ | (2) |
| $ \begin{array}{l} {J_d}{{\ddot \theta }_y} + k\left[ { - \left( {x - {l_1}{\theta _y}} \right){l_1} + \left( {x + {l_2}{\theta _y}} \right){l_2}} \right] - \\ \alpha \left[ {{{\left( {y + {l_1}{\theta _x}} \right)}^2} + {{\left( {x - {l_1}{\theta _y}} \right)}^2}} \right]\left( {x - {l_1}{\theta _y}} \right){l_1} + \\ \alpha \left[ {{{\left( {y - {l_2}{\theta _x}} \right)}^2} + {{\left( {x + {l_2}{\theta _y}} \right)}^2}} \right]\left( {x + {l_2}{\theta _y}} \right){l_2} + \\ c\left[ { - \left( {\dot x - {l_1}{{\dot \theta }_y}} \right){l_1} + \left( {\dot x + {l_2}{{\dot \theta }_y}} \right){l_2}} \right] - {J_{\rm{p}}}\omega {{\dot \theta }_x} = \\ - {J_{\rm{p}}}\omega {\omega _x} - {J_d}{{\dot \omega }_y}, \end{array} $ | (3) |
| $ \begin{array}{l} {J_d}{{\ddot \theta }_x} + k\left[ { - \left( {y + {l_1}{\theta _x}} \right){l_1} + \left( {y - {l_2}{\theta _x}} \right){l_2}} \right] - \\ \alpha \left[ {{{\left( {y + {l_1}{\theta _x}} \right)}^2} + {{\left( {x - {l_1}{\theta _y}} \right)}^2}} \right]\left( {y + {l_1}{\theta _x}} \right){l_1} + \\ \alpha \left[ {{{\left( {y - {l_2}{\theta _x}} \right)}^2} + {{\left( {x + {l_2}{\theta _y}} \right)}^2}} \right]\left( {y - {l_2}{\theta _x}} \right){l_2} + \\ \left. {c - \left( {\dot y + {l_1}{{\dot \theta }_x}} \right){l_1} + \left( {\dot y - {l_2}{{\dot \theta }_x}} \right){l_2}} \right] - {J_{\rm{p}}}\omega {{\dot \theta }_y} = \\ - {J_{\rm{p}}}\omega {\omega _y} - {J_d}{{\dot \omega }_x}. \end{array} $ | (4) |
式中:m为圆盘质量,e为转盘的偏心距,ω为转子的转速,ϕ0为转盘偏心的初始相位,
式(1)~(4)中,方程右端包括转子不平衡力和机动飞行所引起的附加刚度、阻尼和激励力效应,机动飞行效应写成矩阵形式为
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_{\rm{F}}} = {\mathit{\boldsymbol{F}}_{{\rm{F}}1}} + {\mathit{\boldsymbol{F}}_{{\rm{F}}2}} + {\mathit{\boldsymbol{F}}_{{\rm{F}}3}} = \\ \left[ {\begin{array}{*{20}{c}} {m\left( {\omega _x^2 + \omega _z^2} \right)y - m\left( {{\omega _y}{\omega _z} - {{\dot \omega }_x}} \right)z}\\ {m\left( {\omega _x^2 + \omega _y^2} \right)z - m\left( {{\omega _y}{\omega _z} + {{\dot \omega }_x}} \right)y}\\ 0\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {2m{\omega _x}\dot z}\\ {2m{\omega _x}\dot y}\\ 0\\ 0 \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} { - m\left( {{{\ddot y}_{\rm{F}}} + {\omega _z}{{\dot x}_{\rm{F}}} - {\omega _x}{{\dot z}_{\rm{F}}} + {\omega _x}{\omega _y}x + {{\dot \omega }_z}x} \right)}\\ { - m\left( {{{\ddot z}_{\rm{F}}} - {\omega _y}{{\dot x}_{\rm{F}}} + {\omega _x}{{\dot y}_{\rm{F}}} + {\omega _x}{\omega _z}x - {{\dot \omega }_y}x} \right)}\\ { - {J_{\rm{p}}}\omega {\omega _z} - {J_d}{{\dot \omega }_y}}\\ {{J_{\rm{p}}}\omega {\omega _y} - {J_d}{{\dot \omega }_z}} \end{array}} \right]. \end{array} $ |
式中:FF1为附加刚度效应,FF2为附加阻尼效应,FF3为附加惯性力及附加惯性力矩.通常情况下,附加刚度效应远小于系统固有的刚度,附加阻尼效应与飞机横滚运动有直接关系.
设F1为飞机做水平盘旋运动时对转盘引起的附加激励力,F2为飞机做俯冲-拉起运动时对转盘引起的附加激励力,F3为飞机做横滚运动时对转盘引起的附加激励力,且
| $ {\mathit{\boldsymbol{F}}_1} = {\left[ {\begin{array}{*{20}{l}} 0&{m{\omega _y}{{\dot x}_{\rm{F}}}}&0&{{J_{\rm{p}}}\omega {\omega _y}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{F}}_2} = {\left[ {\begin{array}{*{20}{c}} { - m{\omega _z}{{\dot x}_{\rm{F}}}}&0&{ - {J_{\rm{p}}}\omega {\omega _z}}&0 \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{F}}_3} = {\left[ {\begin{array}{*{20}{l}} {2m{\omega _x}\dot z}&{2m{\omega _x}\dot y}&0&0 \end{array}} \right]^{\rm{T}}}. $ |
由此可得机动飞行对转子系统产生的附加激励力.方程的推导中并没有将转盘的欧拉角假设成小量.因此该模型不仅适用于简单飞行状况,还能用于飞机在空间任意飞行状态的研究.
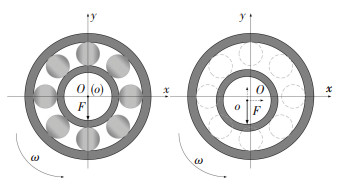
1.2 滚动轴承时变刚度模型如图 2所示,设时间t0=0时转轴轴心与轴承内圈轴心重合于坐标零点,当t1=t0+Δt时,轴承内圈随转轴运动产生位移Δ1=[δx1 δy1 φx1 φy1]T,利用Hertz接触理论和Harris滚动轴承模型,采用文献[18]计算得到的轴承主对角刚度矩阵K,即可得到t1时刻转轴对轴承的作用力F=Δ1K,将轴承对转子的支反力-F=[-Fx1-Fy1-Mx1-My1]T引入系统整体有限元模型,即可计算当t2=t1+Δt时的转轴位置Δ2=[δx2 δy2 φx2 φy2]T,以此类推即可得到轴承刚度随转子运动产生的时变规律及转子受轴承时变刚度影响所产生的非线性动力学行为.
|
图 2 滚动轴承时变刚度模型 Fig. 2 Bearing model with time-varying stiffness |
采用Rayleigh梁进行有限元建模,得动力学微分方程为
| $ \mathit{\boldsymbol{M\ddot X}} + \left( {\mathit{\boldsymbol{C}} - \omega \mathit{\boldsymbol{G}}} \right)\mathit{\boldsymbol{\dot X}} + \mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{F}}_{\rm{e}}} + {\mathit{\boldsymbol{F}}_{\rm{F}}} + \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{F}}_{\rm{P}}} + {\mathit{\boldsymbol{F}}_{\rm{h}}}. $ |
式中:Fp为单点碰摩力矩阵,采用文献[10]的新型碰摩模型计算获得,另有不平衡力矩阵Fe、重力矩阵G及轴承力矩阵Fb为
| $ {\mathit{\boldsymbol{F}}_{\rm{e}}} = {\left[ \begin{array}{l} 0,0,0,0,{m_1}{e_1}{\omega ^2}\cos \omega t,{m_1}{e_1}{\omega ^2}\sin \omega t,\\ 0,0,0,0,0,0,0,0,0,0,{m_2}{e_2}{\omega ^2}\cos \omega t,\\ {m_2}{e_2}{\omega ^2}\sin \omega t,0,0,0,0,0,0 \end{array} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{G}} = {\left[ \begin{array}{l} 0,0,0,0,0, - {m_1}g,0,0,0,0,0,0,\\ 0,0,0,0,0, - {m_2}g,0,0,0,0,0,0 \end{array} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{F}}_{\rm{b}}} = {\left[ \begin{array}{l} - {F_{x1}}, - {F_{y1}},0,0,0,0,0,0,0,0,0,0,\\ 0,0,0,0,0,0,0,0, - {F_{x2}}, - {F_{y2}},0,0 \end{array} \right]^{\rm{T}}}. $ |
本文仅考虑系统在竖直平面内迅速爬升-俯冲的飞行状态,故引入爬升-俯冲机动载荷矩阵
| $ {\mathit{\boldsymbol{F}}_{\rm{h}}} = {\left[ \begin{array}{l} 0,0,0,0,0,{m_1}{\omega _x}v,0,{J_{{\rm{pl}}}}\omega {\omega _x},0,0,\\ 0,0,0,0,0,0,0,{m_2}{\omega _x}v,0,{J_{{\rm{p}}2}}\omega {\omega _x},0,\\ {m_{{\rm{bl}}}}{\omega _x}v,0,{m_{{\rm{b}}2}}{\omega _x}v \end{array} \right]^{\rm{T}}}. $ | (8) |
式中: v为航行速度,ωx为俯仰角速度.
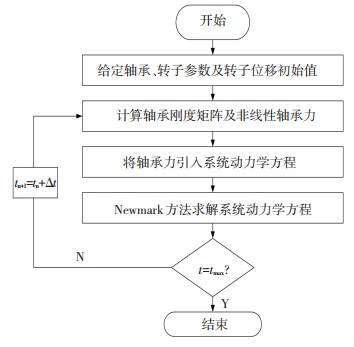
使用Newmark-β法对系统动力学方程进行求解,计算过程如图 3所示.
|
图 3 系统动力学方程求解流程图 Fig. 3 Flow chart of the dynamics equations |
轴承选用7204C角接触球轴承.转轴弹性模量E=209 GPa,泊松比μ=0.3,材料密度ρ=7 850 kg/m3,转子结构参数见表 1.
| 表 1 转子结构参数 Tab. 1 Structure parameters of rotor |
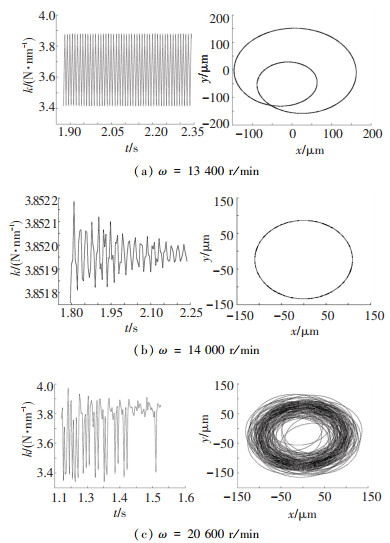
图 4给出了不同转速下轴承径向刚度时变规律图及系统轴心轨迹图.不考虑机动载荷及碰摩故障的影响,图 4(a)、(b)、(c)分别表示系统处于拟周期运动、单周期运动、混沌运动状态时轴承刚度的时变规律.可见,当系统处于单周期运动状态时,轴承刚度的波动范围较小,且随着工作时间的推移刚度趋于稳定,此时轴承刚度可近似为定值;当系统处于拟周期运动状态时,轴承刚度呈周期性变化,刚度变化范围较单周期运动时有所增大;当系统进入混沌状态后,轴承刚度的变化也失去周期性,刚度波动幅度进一步增大.
|
图 4 轴承时变刚度与系统响应 Fig. 4 Time-varying stiffness and response of the system |
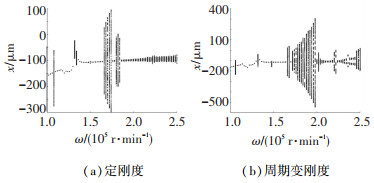
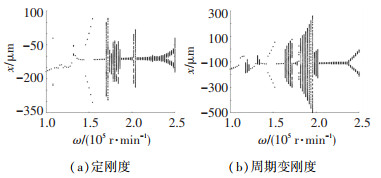
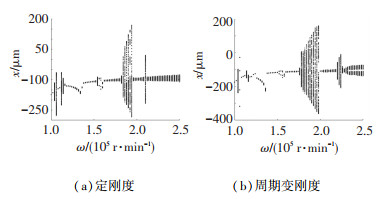
图 5~7为定刚度轴承-转子系统和周期时变刚度轴承-转子系统的分岔图.其中图 5未考虑机动载荷及碰摩故障的影响,图 6中仅引入机动载荷G=4,图 7中仅考虑碰摩刚度Kr=3×106 N/m.对比图 5与图 8(a)、图 6与图 8(b)、图 7与图 9可见,考虑轴承时变刚度的转子系统模型在各个参数影响下均表现出更丰富的非线性动力学状态. 图 9中三维频谱图横坐标频率比(Frequency ratio)代表系统共振频率与主频率比值.
|
图 5 不同轴承刚度下系统响应 Fig. 5 System response under different bearing stiffness |
|
图 6 G=4时不同轴承刚度下系统响应 Fig. 6 System response under different bearing stiffness for G=4 |
|
图 7 Kr=3×106 N/m时不同轴承刚度下系统响应 Fig. 7 System response under different bearing stiffness for Kr=3×106 N/m |
|
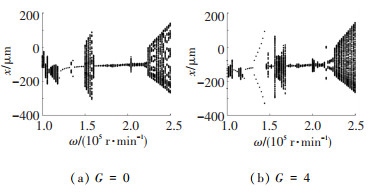
图 8 变刚度轴承-转子系统分岔图 Fig. 8 Bifurcation diagram of bearing-rotor system with variable stiffness |
|
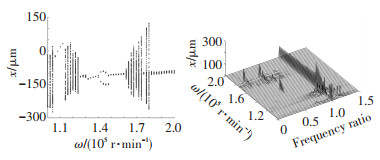
图 9 Kr=3×106 N/m时系统响应 Fig. 9 Response of the rotor system for Kr=3×106 N/m |
在转速低于15 000 r/min及高于22 600 r/min区间,系统产生大量倍周期分岔现象,且整体倍周期分岔点向低转速方向平移.轴承时变刚度对转子系统在低转速区间的影响不仅适用于航空发动机,也适用于离心机及压缩机等工业机械,而其对高转速区间的影响也是提高转子系统最高转速的限制条件之一.
综上可见,以往将系统中轴承刚度视为定值或周期变化值所建立的模型并不能准确表述系统所有的运动状态,有必要建立轴承刚度随转子瞬时运动状态改变而改变的系统模型.
2.2 机动载荷对变刚度轴承-转子系统的影响不考虑碰摩故障的影响,设G=ωxv/g为俯仰机动载荷. 图 8所示分别为不含机动载荷(G=0)和含机动载荷(G=4)时系统的整体分岔图.可见,当转速位于ω=10 000~12 000r/min时,系统稳定性提高,更多转速区间表现为单周期运动;当转速为ω=12 000~15 000 r/min时,系统分岔点提前,且含机动载荷时系统的倍周期运动区间更大,转子轴心轨迹轴向位移增大;当转速为ω=15 000~ 25 000 r/min时,系统分岔增加,稳定区间减小.可见,引入机动载荷的影响后,系统动态特性产生了较为显著的变化.
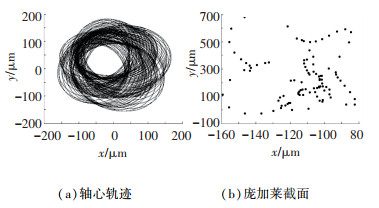
图 10为ω=16 000 r/min,机动载荷G=2时系统的轴心轨迹及庞加莱截面图.结合图 8可知,在机动载荷G=0和G=4时,系统表现为单周期运动或拟周期运动;当G=2时系统表现为混沌运动,可见在该转速区间特定机动载荷会对系统产生较大的影响.
|
图 10 G=2时系统在竖直方向上的振动响应 Fig. 10 Vertical response of the system for G=2 |
综上可见,在低转速下,机动载荷能在一定程度上提高系统的稳定性,因为在低转速下机动载荷的对系统施加的竖直方向上的离心力抑制了轴承非线性力对系统的影响.在中高转速区间特定机动载荷会导致系统进入混沌状态,应尽量避免.在超高转速区间,变刚度轴承的非线性力对系统的影响占据主导地位,机动载荷的影响相对减小.其中,将ω=10 000~14 000 r/min视为相对低转速区间,将ω=14 000~18 000 r/min视为中转速区间,将ω=18 000~22 000 r/min视为高转速区间,将ω=22 000~25 000 r/min视为超高转速区间.
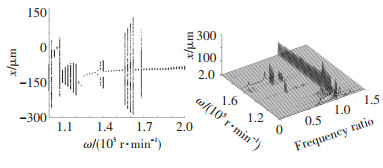
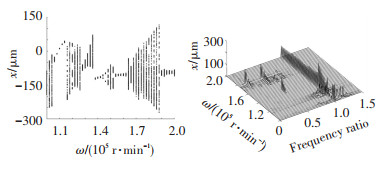
2.3 机动飞行下碰磨转子系统动力学分析考虑节点5处发生单点碰摩,图 9、11、12分别为不同碰摩刚度下系统全局分岔图和三维频谱图.由分岔图可见,当转速低于12 400 r/min时,系统运动状态受碰摩刚度影响较小;当转速高于12 400 r/min时,随着碰摩刚度的提高,系统的动力学特性变得愈加的复杂,分岔及混沌区间增加,系统稳定运动区间减小.
|
图 11 Kr=1×106 N/m时系统响应 Fig. 11 Response of the rotor system for Kr=1×106 N/m |
|
图 12 Kr=5×106 N/m时系统响应 Fig. 12 Response of the rotor system for Kr=5×106 N/m |
由频谱图可见,当转速低于12 400 r/min时,系统产生超谐共振,频率成分主要包含ω、1.14ω及1.29ω;当转速高于12 400 r/min后,频率成分以亚谐共振为主,包括0.14ω、0.43ω、0.5ω及0.71ω等,且随碰摩刚度增大频率成分增多,振幅增大.
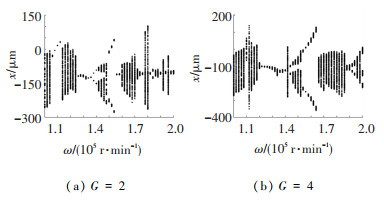
设碰摩刚度Kr=3×106 N/m,图 13为不同机动载荷下转子系统全局分岔.对比图 9可见,当系统存在碰摩故障时,随着机动载荷提高,系统稳定区间减少,倍周期运动区间增加,且在多个转速区间表现出更加复杂的分岔现象.由此可知,机动载荷的提高一定程度上等效于增大了系统的碰磨量.
|
图 13 Kr=3×106 N/m时不同机动载荷下系统响应 Fig. 13 Response of the system under different maneuvering loads for Kr=3×106 N/m |
1) 轴承时变刚度不仅对处于正常工作转速区间的转子系统动力学状态存在影响,也是限制转子系统最高转速的因素之一.为准确描述轴承、转子非线性动力学间的相互影响,有必要建立轴承刚度随转子瞬时运动状态改变而改变的系统模型.
2) 在机动载荷的作用下,系统产生的更加复杂的非线性现象.随着机动载荷的增加,系统整体稳定运动区间减少.在低转速区间,提高机动载荷能一定程度上提高系统稳定性,且在中高转速下特定机动载荷能导致系统产生强烈的非线性现象,在超高转速区间轴承非线性力的作用超过机动载荷对系统的影响.
3) 碰摩故障会对机动飞行状态下的转子系统产生明显的影响.随着碰摩刚度的提高,系统的分岔和混沌运动区间增加,系统运动稳定性降低,且碰摩故障对系统稳定性的影响随转速的提高而增大.系统频率成分以亚谐共振为主,当碰摩故障达到一定程度时会导致系统损毁失效.提高机动载荷一定程度上等效于增大了系统的碰磨量.
| [1] |
徐敏, 廖明夫. 机动飞行条件下带挤压油膜阻尼器的Jeffcott转子系统的振动特性[J]. 航空动力学报, 2003, 18(3): 394. XU Min, LIAO Mingfu. The vibration performance of the Jeffcott rotor system with SFD in maneuver flight[J]. Journal of Aerospace Power, 2003, 18(3): 394. DOI:10.3969/j.issn.1000-8055.2003.03.017 |
| [2] |
HARSHA S P. Nonlinear dynamic analysis of a high-speed rotor supported by rolling element bearings[J]. Journal of Sound & Vibration, 2006, 290(1): 65. DOI:10.1016/j.jsv.2005.03.008 |
| [3] |
LIEW H V, LIM T C. Analysis of time-varying rolling element bearing characteristics[J]. Journal of Sound & Vibration, 2005, 283(3/4/5): 1163. DOI:10.1016/j.jsv.2004.06.022 |
| [4] |
PETERSEN D, HOWARD C, PRIME Z. Varying stiffness and load distributions in defective ball bearings: analytical formulation and application to defect size estimation[J]. Journal of Sound & Vibration, 2015, 337: 284. DOI:10.1016/j.jsv.2014.10.004 |
| [5] |
曹宏瑞, 李亚敏, 何正嘉, 等. 高速滚动轴承-转子系统时变轴承刚度及振动响应分析[J]. 机械工程学报, 2014, 50(15): 73. CAO Hongrui, LI Yamin, HE Zhengjia, et al. Time varying bearing stiffness and vibration response analysis of high speed rolling bearing-rotor systems[J]. Journal of Mechanical Engineering, 2014, 50(15): 73. DOI:10.3901/JME.2014.15.073 |
| [6] |
CAO Hongrui, LI Yamin, CHEN Xuefeng. A new dynamic model of ball-bearing rotor systems based on rigid body element[J]. Journal of Manufacturing Science and Engineering, 2016, 138(7): 071007-1. DOI:10.1115/1.4032582 |
| [7] |
WU Hao, ZHOU Qiong, ZHANG Zhiming, et al. Vibration analysis on the rolling element bearing-rotor system of an air blower[J]. Journal of Mechanical Science & Technology, 2012, 26(3): 653. DOI:10.1007/s12206-011-1201-6 |
| [8] |
BATAILLY A, LEGRAND M, CARTRAUD P, et al. Assessment of reduced models for the detection of modal interaction through rotor stator contacts[J]. Journal of Sound and Vibration, 2010, 329(26): 5546. DOI:10.1016/j.jsv.2010.07.018 |
| [9] |
GROLL G, EWINS D J. The harmonic balance method with arc-length continuation in rotor/stator contact problems[J]. Journal of Sound and Vibration, 2001, 241(2): 223. DOI:10.1006/jsvi.2000.3298 |
| [10] |
陈果, 王海飞. 新型叶片-机匣碰摩模型及其验证[J]. 航空动力学报, 2015, 30(4): 954. CHEN Guo, WANG Haifei. A new blade-casing rubbing model and its verification[J]. Journal of Aerospace Power, 2015, 30(4): 954. DOI:10.13224/j.cnki.jasp.2015.04.023 |
| [11] |
MA Hui, YU Tao, HAN Qingkai, et al. Time-frequency features of two types of coupled rub-impact faults in rotor systems[J]. Journal of Sound and Vibration, 2009, 321(3/4/5): 1109. DOI:10.1016/j.jsv.2008.09.054 |
| [12] |
YANG Yongfeng, REN Xingmin, QIN Weiyang, et al. Analysis on the nonlinear response of cracked rotor in hover flight[J]. Nonlinear Dynamics, 2010, 61(1/2): 183. DOI:10.1007/s11071-009-9640-7 |
| [13] |
杨永锋, 任兴民, 秦卫阳. 俯冲拉起下裂纹转子的非线性[J]. 振动与冲击, 2007, 26(4): 21. YANG Yongfeng, REN Xingmin, QIN Weiyang. Nonlinear response analysis of a cracked Jeffcott rotor in action of dive-hike[J]. Journal of Vibration and Shock, 2007, 26(4): 21. DOI:10.3969/j.issn.1000-3835.2007.04.006 |
| [14] |
祝长生, 陈拥军. 机动飞行时航空发动机转子系统的振动特性[J]. 航空学报, 2006, 27(5): 835. DOI:10.3321/j |
| [15] |
祝长生, 陈拥军. 机动飞行时发动机转子系统动力学统一模型[J]. 航空动力学报, 2009, 24(2): 371. ZHU Changsheng, CHEN Yongjun. General dynamic model of aeroengine's rotor system during maneuvering flight[J]. Journal of Aerospace Power, 2009, 24(2): 371. DOI:10.13224/j.cnki.jasp.2009.02.012 |
| [16] |
HOU Lei, CHEN Yushu, CAO Qingjie. Turing maneuver caused response in an aircraft rotor-ball bearing system[J]. Nonlinear Dynamics, 2015, 79(1): 229. DOI:10.1007/s11071-014-1659-8 |
| [17] |
HOU Lei, CHEN Yushu, CAO Qingjie. Nonlinear vibration phenomenon of an aircraft rub-impact rotor system due to hovering flight[J]. Commun Nonlinear Sci Numer Simulat, 2014, 19(1): 286. DOI:10.1016/j.cnsns.2013.06.023 |
| [18] |
王美令.不对中转子系统的动力学机理及其振动特性研究[D].沈阳: 东北大学, 2013. WANG Meiling. Dynmamics and vibration characteristics of misaligned rotor systems[D]. Shenyang: Northeastern University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10145-1016011931.htm |
 2020, Vol. 52
2020, Vol. 52



