2. 平壤出版印刷综合大学 机械工程学院,平壤 999093
2. School of Mechanical Engineering, University of Publishing and Printing Pyongyang, Pyongyang 999093, DPR of Korea
空气箔片轴承是一种采用柔性支撑,以空气为润滑剂的自作用式动压气体轴承.一系列波拱不仅提供弹性支撑,还提供阻尼.在波箔制造过程中,波拱与波拱的连接桥会形成一个过渡圆角.由载荷产生的弯矩也作用在过渡圆角,该弯矩有利于波拱的变形.因此,过渡圆角对空气箔片轴承的刚度有影响.关于箔片几何结构对箔片轴承性能的影响,Walowit [1]和Heshmat [2-3]等进行了大量的实验和理论研究,提出了波箔结构的弹性模型,并研究了箔片轴承的稳态特性,但没有考虑顶层箔片与壳体以及波箔的摩擦力. 1999年,Iordanoff[4]考虑波箔与平箔间的接触摩擦作用,建立了波拱一端固定,一端自由以及两端都自由的刚度计算模型. 2003年,Carpino等[5]将结构阻尼设为黏性阻尼,开发了一种有限元模型,解释了库仑摩擦对箔片轴承性能的影响. 2007年,Lez等[6]使用有限元软件进行了更精确的数值分析,考虑了箔片与壳体之间以及波箔与顶层箔片之间的摩擦力,研究了箔片结构的静态和动态特性,但没有考虑波拱结构的影响. 2010年,Feng等[7]认为波箔的波拱可简化为两个刚性连接件和一个水平间隔开的弹簧.但所提出的模型忽略了波拱的切向位移,高估了波拱柔性. Peng等[8]将波箔结构模拟为弹簧和阻尼器,研究了波拱之间的相互作用,但忽略了顶层箔片和波箔之间的摩擦. Ku等[9]考虑了波箔与壳体或顶层箔片之间的摩擦力和各波拱之间的相互作用,开发了柔性箔片轴承的综合分析模型.该模型还考虑了可变载荷分布,摩擦力和波拱几何形状等对轴承刚度的影响,但没有考虑过渡圆角的作用. 2008年,Hryniewicz等[10]的数值模型考虑了在任意压力载荷下波箔和顶层箔片之间的相互作用、波拱之间的相互作用以及波箔与壳体间的摩擦力.在其模型中,通过定义3种不同的边界约束条件来分析波拱的偏转,并将结果与之前的有限元结果进行比较.但该模型忽略了波拱和顶层箔片之间局部摩擦和过渡圆角的影响. 2014年,Abdelrasoul等[11]在箔片气体推力轴承的静态分析中,考虑到波拱之间的连接桥可能会发生横向偏移并与轴承壳体表面分离的情况,构建了考虑每个波拱弯矩的模型,提出更符合现实情况的边界条件. 2016年,Lehn等[12]首次进行具有过渡圆角的波拱的研究.模拟了一个厚度的二维壳体,包括顶层箔片、波箔和过渡圆角,并为箔片气体推力轴承提供完全耦合的弹性气体动力学模型.此外,还讨论了摩擦力、接触的影响以及不同波拱相互作用机制.但没有具体提到过渡圆角本身对整个箔片轴承刚度的影响.
本文研究有过渡圆角的波拱结构的刚度特性.基于弹性变形理论,考虑了波箔与壳体或顶层箔片之间的摩擦力以及各波拱之间的相互作用,构建有过渡圆角的波拱的弯矩方程组,推导出箔片变形公式.通过与既有的箔片模型进行比较,验证本模型的有效性,结果表明,箔片轴承的刚度特性研究不应忽略过渡圆角的作用.
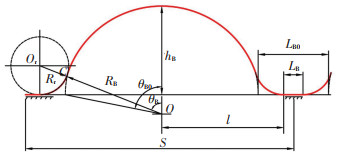
1 理论分析 1.1 波拱的几何结构由于箔片轴承的制造工艺,波箔片的两个波拱间的连接桥会产生一个过渡圆角,但这个过渡圆角在很多理论模型中常常被忽略. 图 1为一个平行于xy平面的具有过渡圆角的波拱结构.
|
图 1 具有过渡圆角的波拱结构 Fig. 1 Geometry of a single bump foil with rounding |
点O是波拱的圆心,Or是过渡圆圆心,点C是过渡圆角半径Rr和波拱半径RB之间的相切点. θB0和LB0分别是无过渡圆角的波拱弧角和波拱连接板长度,θB和LB分别是具有过渡圆角的波拱弧角和波拱连接板长度,hB是波拱高度,l是波拱半波长度,s是波拱单元长度.
波拱弧角θB有如下关系:
| $ \cos {\theta _{\rm{B}}} = \frac{{\left( {{R_{\rm{B}}} \cdot \cos {\theta _{{\rm{B}}0}} + {R_{\rm{r}}}} \right)}}{{\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)}}. $ |
波拱半波长l和波拱连接板LB可表示为
| $ l = \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}}, $ |
| $ {L_{\rm{B}}} = {L_{{\rm{B}}0}} - 2 \cdot \left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{B}}}\sin {\theta _{{\rm{B}}0}}} \right]. $ |
因此,具有过渡圆角的波拱的几何尺寸完全可由RB、θB0、LB0和Rr决定.波拱高度hB被视为相关参数(它可以由RB、Rr和θB来确定).当Rr→0时,模型变为无过渡圆角的波拱模型,因此,无过渡圆角的波拱模型是一种特殊形式.
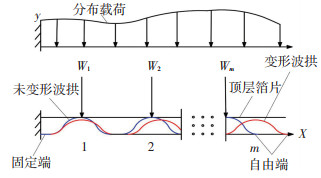
1.2 波拱的结构模型图 2是波箔在任意压力负载下的变形情况.波箔的左端固定,其右端可以在x方向(水平方向)和y方向(垂直方向)上自由移动,现假设顶层箔片紧贴在波箔的波拱顶部,设Wi为作用在第i个波拱顶部中心单位长度上的垂直载荷,y方向的局部挠度是δWi. δWi取决于波拱和壳体之间的滑动摩擦因数μ以及波拱和顶层箔片之间的滑动摩擦因数η,箔片将在载荷Wi的作用下向自由端滑动.
|
图 2 分布静载荷下箔片的变形情况 Fig. 2 Deflection of bump foil strip under static load |
本文作如下假设:
1) 顶层箔片紧贴波箔片的运动,但不会影响波拱变形;
2) 两个波拱间的连接桥不会偏离壳体表面;
3) 箔片的变形都是弹性的,且不会发生永久变形;
4) 过渡圆角半径Rr与波拱半径RB之间的相切点C位于两个中心的直线上;
5) 过渡圆角变形时,忽略过渡圆角与壳体的接触效应;
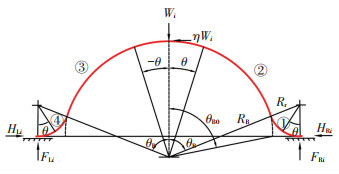
在图 3中,波箔模型分为4个部分:两个波拱弧角(②、③)和两个过渡圆角(①、④).
|
图 3 第i个波拱的受力分析 Fig. 3 Force analysis of the i-th bump in the bump foil strip |
FLi和FRi分别是第i个波拱左、右两端处所受的支座反力;HLi和HRi分别是第i个波拱左、右两端受到的切向力.第i个波拱的右端处的力平衡条件为
| $ {P_{{\rm{R}}i}} = {H_{{\rm{R}}i}} - \mu {F_{{\rm{R}}i}}. $ | (1) |
PRi是从第i+1个波拱左端通过连接桥传递到第i个波拱右端的作用力.同时,在第i个波拱的右端,还有从i+1个到N个波拱的阻碍第i个波拱滑动的作用力:
| $ {T_{{\rm{R}}i}} = \sum\limits_{n = i + 1}^{n = N} {\left( {\mu + \eta } \right){W_n}} . $ |
为确定第i个波拱的运动状态,需要对比传递力PRi和抵抗力TRi,这与Hryniewicz、Wodtke、Olszewski等[10]的方法类似.
第i个波拱的每个组成部分的任意θ单位宽度上所受的弯矩为
| $ \begin{array}{*{20}{c}} {{M_{1i}}\left( \theta \right) = - {F_{{\rm{R}}i}}{R_{\rm{r}}}\sin \theta + {H_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right),}\\ {0 < \theta \le {\theta _{\rm{B}}};} \end{array} $ | (2) |
| $ \begin{array}{l} {M_{2i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{B}}}\sin \theta } \right] + \\ \;\;\;\;\;\;{H_{{\rm{R}}i}}\left[ {{R_{\rm{r}}}\left( {1 - \cos {\theta _{\rm{B}}}} \right) + {R_{\rm{B}}}\left( {\cos \theta - \cos {\theta _{\rm{B}}}} \right)} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \theta \le {\theta _{\rm{B}}}; \end{array} $ | (3) |
| $ \begin{array}{l} {M_{3i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{B}}}\sin \theta } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{H_{{\rm{R}}i}}\left[ {{R_{\rm{r}}} + {R_{\rm{B}}}\cos \theta - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{W_i}{R_{\rm{B}}}\sin \theta - \eta {W_i}{R_{\rm{B}}}\left( {1 - \cos \theta } \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\theta _{\rm{B}}} \le \theta \le 0; \end{array} $ | (4) |
| $ \begin{array}{l} {M_{4i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {2\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{r}}}\sin \theta } \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\eta {W_i}\left[ {{R_{\rm{B}}} + {R_{\rm{r}}}\cos {\theta _{\rm{B}}} - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{W_i}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{r}}}\sin \theta } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;{H_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \theta \le {\theta _{\rm{B}}}. \end{array} $ | (5) |
式中:θB是第i个波拱的顶部中心点和C点形成的弧角.由于波箔片厚度t与波拱半径RB相比非常小,波拱可以看作一个薄的弯曲梁.当RB/t>10时,可以忽略法向力和剪切力,由此产生的误差通常<1%,很少超过5%[13].本文的RB/t的比值为186.7.因此,拉伸和剪切力的应变忽略不计,弹性应变能表示为[14-15]
| $ U = \int_0^\theta {\frac{{{M^2}}}{{2DL}}} R{\rm{d}}\theta . $ |
第i个波拱的抗弯刚度D可定义如下:
| $ D = E{t^3}/\left( {12\left( {1 - {\nu ^2}} \right)} \right). $ |
式中:E是箔片的弹性模量,t和ν分别是箔片的厚度和泊松比.
设δi是由作用力HRi和FRi引起的弹性挠度,根据卡斯蒂利亚诺的第二定理,可得
| $ \begin{array}{l} {\delta _{{\rm{H}}i}} = \frac{{\partial U}}{{\partial {H_{{\rm{R}}i}}}} = \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{1i}}}}{{DL}} \cdot \frac{{\partial {M_{1i}}}}{{\partial {H_{{\rm{R}}i}}}}{R_{\rm{r}}}{\rm{d}}\theta } + \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{2i}}}}{{DL}} \cdot \frac{{\partial {M_{2i}}}}{{\partial {H_{{\rm{R}}i}}}}{R_{\rm{B}}}{\rm{d}}\theta } + \\ \;\;\;\;\;\;\;\;\int\limits_{ - {\theta _{\rm{B}}}}^0 {\frac{{{M_{3i}}}}{{DL}} \cdot \frac{{\partial {M_{3i}}}}{{\partial {H_{{\rm{R}}i}}}}{R_{\rm{B}}}{\rm{d}}\theta } + \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{4i}}}}{{DL}} \cdot \frac{{\partial {M_{4i}}}}{{\partial {H_{{\rm{Ri}}}}}}{R_{\rm{r}}}{\rm{d}}\theta } , \end{array} $ |
| $ \begin{array}{l} {\delta _{{\rm{V}}i}} = \frac{{\partial U}}{{\partial {F_{{\rm{R}}i}}}} = \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{1i}}}}{{DL}} \cdot \frac{{\partial {M_{1i}}}}{{\partial {F_{{\rm{R}}i}}}}{R_{\rm{r}}}{\rm{d}}\theta } + \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{2i}}}}{{DL}} \cdot \frac{{\partial {M_{2i}}}}{{\partial {F_{{\rm{R}}i}}}}{R_{\rm{B}}}{\rm{d}}\theta } + \\ \;\;\;\;\;\;\;\;\int\limits_{ - {\theta _{\rm{B}}}}^0 {\frac{{{M_{3i}}}}{{DL}} \cdot \frac{{\partial {M_{3i}}}}{{\partial {F_{{\rm{R}}i}}}}{R_{\rm{B}}}{\rm{d}}\theta } + \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{4i}}}}{{DL}} \cdot \frac{{\partial {M_{4i}}}}{{\partial {F_{{\rm{R}}i}}}}{R_{\rm{r}}}{\rm{d}}\theta } . \end{array} $ |
如果假设第i个波拱的右端被固定,则由边界条件(δHi=0,δVi =0)得到下列矩阵方程:
| $ \left[ {\begin{array}{*{20}{c}} {{D_1}}&{{D_2}}\\ {{D_4}}&{{D_5}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{F_{{\rm{R}}i}}}\\ {{H_{{\rm{R}}i}}} \end{array}} \right\} = - \left\{ {\begin{array}{*{20}{c}} {{D_3}}\\ {{D_6}} \end{array}} \right\}{W_i}. $ | (6) |
式中:系数D1~D6仅是θB的函数.式(6)中的HRi、FRi解出后,代入式(1)获得PRi.为了判定第i个波拱的运动状态,需比较抵抗力TRi和传递力PRi的大小,判定如下:
如果PRi≥TRi,则第i个波拱的右端向右移动,则传递力为
| $ {P_{{\rm{R}}i}} = {T_{{\rm{R}}i}}; $ |
如果PRi < TRi,第i个波拱的右端被固定,则传递力PRi保持为
| $ {P_{{\rm{R}}i}} = {H_{{\rm{R}}i}} - \mu {F_{{\rm{R}}i}}. $ |
通过上述两个条件,第i个波拱所受的弯矩方程(2)~(5)可由PRi和FRi表示
| $ \begin{array}{l} {M_{1i}}\left( \theta \right) = - {F_{{\rm{R}}i}}{R_{\rm{r}}}\sin \theta + {P_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mu {F_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;0 < \theta \le {\theta _{\rm{B}}}; \end{array} $ | (7) |
| $ \begin{array}{l} {M_{2i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{B}}}\sin \theta } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{P_{{\rm{R}}i}}\left[ {{R_{\rm{r}}} + {R_{\rm{B}}}\cos \theta - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mu {F_{{\rm{R}}i}}\left[ {{R_{\rm{r}}} + {R_{\rm{B}}}\cos \theta - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \theta \le {\theta _{\rm{B}}}; \end{array} $ | (8) |
| $ \begin{array}{l} {M_{3i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{B}}}\sin \theta } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{{\rm{R}}i}}\left[ {{R_{\rm{r}}} + {R_{\rm{B}}}\cos \theta - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu {F_{{\rm{R}}i}}\left[ {{R_{\rm{r}}} + {R_{\rm{B}}}\cos \theta - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{W_i}{R_{\rm{B}}}\sin \theta - \eta {W_i}{R_{\rm{B}}}\left( {1 - \cos \theta } \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\theta _{\rm{B}}} \le \theta \le 0; \end{array} $ | (9) |
| $ \begin{array}{l} {M_{4i}}\left( \theta \right) = - {F_{{\rm{R}}i}}\left[ {2\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{r}}}\sin \theta } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{P_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right) + \mu {F_{{\rm{R}}i}}{R_{\rm{r}}}\left( {1 - \cos \theta } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{W_i}\left[ {\left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\sin {\theta _{\rm{B}}} - {R_{\rm{r}}}\sin \theta } \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\eta {W_i}\left[ {{R_{\rm{B}}} + {R_{\rm{r}}}\cos {\theta _{\rm{B}}} - \left( {{R_{\rm{B}}} + {R_{\rm{r}}}} \right)\cos {\theta _{\rm{B}}}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \theta \le {\theta _{\rm{B}}}. \end{array} $ | (10) |
FRi可以通过边界条件(δVi=0)和方程(7)~(10)求解:
| $ {F_{{\rm{R}}i}} = - \left( {{D_8}{P_{{\rm{R}}i}} + {D_9}{W_i}} \right)/{D_7}. $ |
式中D7~D9为系数.
一旦确定了第i个波拱右端的PRi和FRi,根据卡斯蒂利亚诺第二定理得到波拱的顶点挠度:
| $ {\delta _{{W_i}}} = \frac{{\partial U}}{{\partial {W_i}}} = \int\limits_{ - {\theta _{\rm{B}}}}^0 {\frac{{{M_{3i}}}}{{DL}} \cdot \frac{{\partial {M_{3i}}}}{{\partial {W_i}}}{R_{\rm{B}}}{\rm{d}}\theta } + \int\limits_0^{{\theta _{\rm{B}}}} {\frac{{{M_{4i}}}}{{DL}} \cdot \frac{{\partial {M_{4i}}}}{{\partial {W_i}}}{R_{\rm{r}}}{\rm{d}}\theta } $ | (11) |
将弯矩方程组代入式(11)得
| $ {\delta _{{W_i}}} = \left( {{D_{10}}{F_{{\rm{R}}i}} + {D_{11}}{P_{{\rm{R}}i}} + {D_{12}}{W_i}} \right)/DL. $ | (12) |
式中,D10~D12为系数.第i个波拱的刚度可以定义为
| $ k_i^{\rm{B}} = {W_i}/{\delta _{{W_i}}}. $ | (13) |
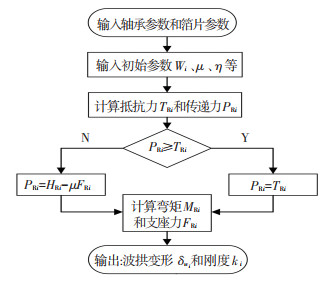
根据式(12)和(13)可以得到每个波拱的变形和刚度.数值求解流程如图 4所示.
|
图 4 波拱模型的流程 Fig. 4 Flow chart of the bump foil model |
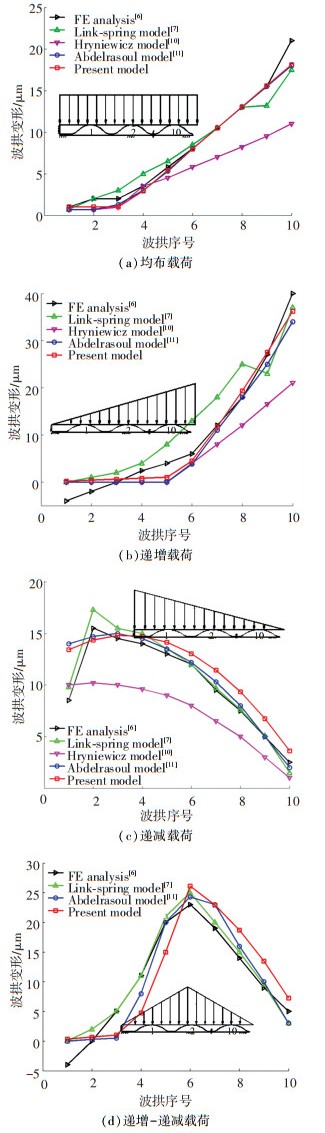
为了验证本文理论模型的有效性,轴承的几何参数选择与文献(Lez等[6],Feng和Kaneko[7],Hryniewicz等[10]和Abdelrasoul[11])中的模型参数相同,如表 1所示.其中波拱数为10.不同载荷下波拱变形情况见图 5.
| 表 1 轴承结构参数 Tab. 1 Geometrical parameters of the bearing |
|
图 5 不同载荷下波拱的变形 Fig. 5 Bumps deflection under various load distributions |
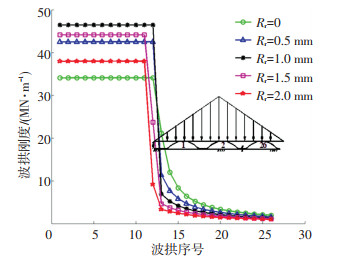
为详细分析每个波拱的刚度特性,采用具有26个波拱的波箔模型,由于递增递减载荷分布最接近箔片实际受力,图 6给出了此载荷下波拱的刚度分布情况.刚度相同的波拱所在的区域为固定区,刚度变化的波拱所在的区域为滑移区.从图 6中可看出,固定区波拱刚度明显高于滑移区波拱刚度.固定区的波拱数量越多,则波箔的刚度越大.在滑移区,波拱刚度先快速下降后逐渐趋于平缓.在4种载荷作用下,自由端的波拱刚度几乎相同.
|
图 6 在不同载荷下带有过渡圆角波拱的刚度 Fig. 6 Bumps stiffness with rounding radius under various loads |
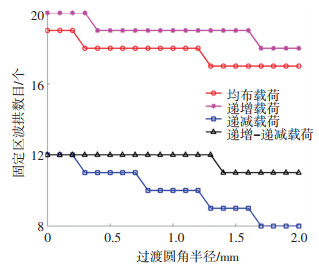
过渡圆角的引入,改变了波箔与轴承壳的接触面积,同时影响波拱的受力和各个波拱之间的传递力.固定区的波拱数量从大到小依次是递增载荷、均布载荷、递增-递减载荷和递减载荷,如图 7所示.随着过渡圆角半径的增大,4种载荷下固定区波拱的数量呈不同等级的阶梯状减少,其中递增载荷、均布载荷、递增-递减载荷和递减载荷下波拱数量分别呈二级、二级、一级、四级阶梯状减少.这说明过渡圆角半径的增大会使波拱更容易滑动.这是因为过渡圆角半径的增大,导致波拱与波拱之间的连接板越来越短,波拱与轴承壁的摩擦接触面积越来越少.
|
图 7 不同过渡圆角半径的固定区波拱数量 Fig. 7 Number of pinned-down bumps with various rounding radius |
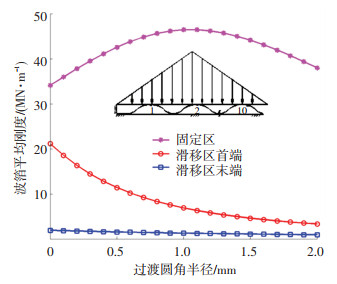
递增-递减载荷下不同过渡圆角半径的波拱刚度分布情况见图 8.随着过渡圆角半径的增大,固定区波拱刚度先增大后减小,存在一个使波拱刚度达到最大的过渡圆角半径;滑移区首端波拱刚度逐渐减小,末端波拱刚度基本不变,这是因为末端波拱接近波箔的自由端,其刚度受过渡圆角半径影响小.
|
图 8 不同过渡圆角半径的波拱刚度 Fig. 8 Bumps stiffness with various rounding radius |
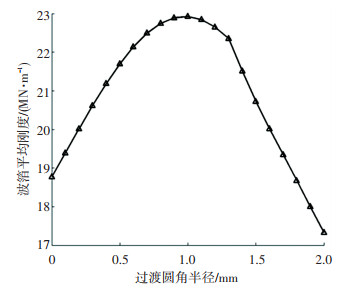
图 9分析了不同过渡圆角半径的波箔平均刚度分布情况.随着过渡圆角半径的增大,波箔平均刚度先增大后减小.对比图 9和图 8可看出,固定区波拱刚度达到最大所对应的过渡圆角半径与波箔平均刚度达到最大所对应的过渡圆角半径非常接近.
|
图 9 不同过渡圆角半径的波箔平均刚度 Fig. 9 Mean stiffness of bump foil with various rounding radius |
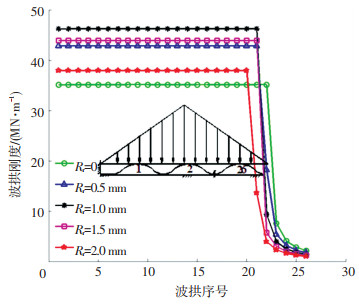
摩擦因数μ=0.300,η=0.300时的波拱刚度分布情况如图 10所示,对比图 6可看出,因为固定区波拱受力时,波拱两端受到的是静摩擦力,随着摩擦因数的增大,固定区的同一过渡圆角的波拱刚度值基本不变,但波拱数量增加;滑移区主要受滑动摩擦力影响,随摩擦因数增大,其波拱数量减少,且滑移区波拱刚度有不同程度的增加,越靠近自由端,刚度受摩擦影响越小.
|
图 10 摩擦因数μ=η=0.3时波拱的刚度 Fig. 10 Bumps stiffness with friction coefficient μ=η=0.3 |
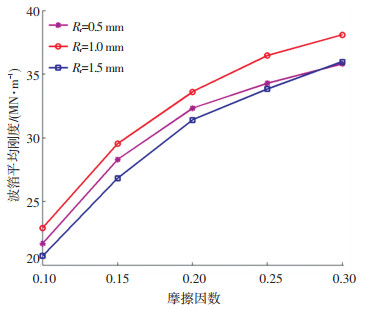
综上所述,波箔平均刚度随着摩擦因数的增大呈现非线性增大,如图 11所示.摩擦因数和过渡圆角半径通过改变固定区波拱的刚度和数量以及滑移区波拱刚度来影响波箔的刚度.这说明过渡圆角半径和摩擦因数这两个参数的不同组合,可以建立具有不同阻尼和刚度的箔片轴承.
|
图 11 不同摩擦因数的波箔平均刚度 Fig. 11 Mean stiffness of bump foil with various friction coefficients |
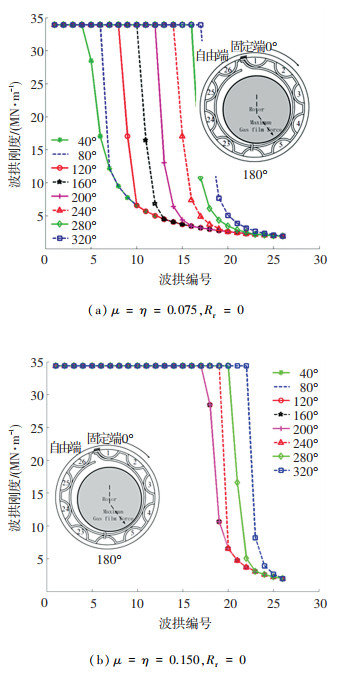
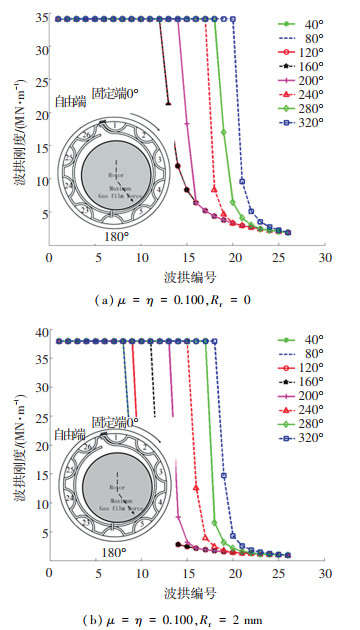
由于波箔气体轴承在实际应用中所受外载荷方向具有很大的随机性,造成气膜力在波箔结构上的分布形式也并不相同,故本文通过改变载荷峰值距固定端的距离模拟不同角度下的受载情况,以研究波箔结构刚度的各向异性.摩擦因数μ=η=0.075时, 不同承载力峰值角度下各个箔拱的刚度变化情况如图 12(a)所示,可以看出, 波箔结构刚度存在较强的各向异性,载荷峰值越靠近固定端,会导致越多的波拱向自由端产生滑移,即使固定区箔拱数量减少,从而降低整体刚度;反之,最大气膜力越靠近自由端,整体刚度越大. 图 12(b)为摩擦因数μ=η=0.150时的波箔结构刚度特性,可以看出,最大气膜力加载角度在200°之前的刚度曲线重合,说明增大摩擦因数可有效改善波箔气体轴承结构刚度的各向异性. 图 13(a)和(b)分别为过渡圆角半径Rr为0和2 mm时的波箔结构刚度特性曲线,二者分别在最大载荷加载角度160°和80°处开始出现箔拱滑移,说明随过渡圆角半径增大,滑移区箔拱数增多使得各向异性增强,但影响程度不如摩擦因数剧烈.可看出,增大摩擦因数和减小过渡圆角半径可为改善波箔气体轴承各向异性提供一定的思路.
|
图 12 不同摩擦因数下加载角度对波拱刚度影响 Fig. 12 Effect of loading angle on the bump stiffness under various friction coefficients |
|
图 13 不同圆角半径下加载角度对波拱刚度影响 Fig. 13 Effect of loading angle on the bump stiffness under various rounding radius |
1) 在4种载荷条件下,随着过渡圆角半径的增大,固定区波拱的数量呈阶梯状减少.
2) 随着过渡圆角半径的增大,固定区波拱的刚度先增大后减小,滑移区波拱的刚度逐渐减小,同时存在一个使波箔平均刚度达到最大的过渡圆角半径.
3) 圆角半径一定条件下,固定区波拱数量随摩擦系数的增大而增多,波箔结构平均刚度呈非线性增大,有效降低了各向异性;摩擦因数一定条件下,过渡圆角半径的增大使各向异性增强,但影响程度不如摩擦因数大.
| [1] |
WALOWIT J A, ANNO J N. Modern development of lubrication mechanics[M]. London: Applied Science Publishers, 1975.
|
| [2] |
HESHMAT H, WALOWIT J A, PINKUS O. Analysis of gas lubricated foil journal bearings[J]. Journal of Lubrication Technology, 1983, 105(4): 647. DOI:10.1115/1.3254697 |
| [3] |
HESHMAT H, WALOWIT J A, PINKUS O. Analysis of gas lubricated compliant thrust bearings[J]. Journal of Lubrication Technology, 1983, 105(4): 638. DOI:10.1115/1.3254696 |
| [4] |
IORDANOFF. Analysis of an aerodynamic compliant foil thrust bearing: method for a rapid design[J]. Journal of Tribology, 1999, 121(4): 816. DOI:10.1115/1.2834140 |
| [5] |
CARPINO M, TALMAGE G. A fully coupled finite element formulation for elastically supported foil journal bearings[J]. Tribology Transactions, 2003, 46(4): 560. DOI:10.1080/10402000308982664 |
| [6] |
LEZ S L, ARGHIR M, FRENE J. Static and dynamic characterization of a bump-type foil bearing structure[J]. Journal of Tribology, 2007, 129(1): 75. DOI:10.1115/1.2390717 |
| [7] |
FENG K, KANEKO S. Analytical model of bump-type foil bearings using a link-spring structure and a finite-element shell model[J]. Journal of Tribology, 2010, 132(2): 021706. DOI:10.1115/1.4001169 |
| [8] |
PENG J P, CARPINO M. Coulomb friction damping effects in elastically supported gas foil bearings[J]. Tribology Transactions, 1994, 37(1): 91. |
| [9] |
KU C P, HESHMAT H. Compliant foil bearing structural stiffness analysis: part Ⅰ: theoretical model including strip and variable bump foil geometry[J]. Journal of Tribology, 1992, 114: 394. DOI:10.1115/1.2920898 |
| [10] |
HRYNIEWICZ P, WODTKE M, OLSZEWSKI A, et al. Structural properties of foil bearings: a closed-form solution validated with finite element analysis[J]. Tribology Transactions, 2008, 52(4): 435. |
| [11] |
ABDELRASOUL M, KANEKO S. A new structural stiffness model for bump-type foil bearings: application to generation Ⅱ gas lubricated foil thrust bearing[J]. Journal of Tribology, 2014, 136(4): 216. |
| [12] |
LEHN A, MAHNER M, SCHWEIZER B. Elasto-gas dynamic modeling of air foil thrust bearings with a two-dimensional shell model for top and bump foil[J]. Tribology International, 2016, 100: 48. DOI:10.1016/j.triboint.2015.11.011 |
| [13] |
BORESI A P, SCHMIDT R J. Advanced mechanics of materials, 6th edition[M]. New York: John Wiley, 2003.
|
| [14] |
TIMOSHENKO S, GOODIER J N. Theory of Elasticity[M]. 2nd edition. New York: McGraw-Hill Book Company, 1951.
|
| [15] |
BEER F P, JOHOSTON E R, DEWOLF J T. Mechanics of Materials, 6th edition[M]. New York: McGraw-Hill Book Company, 2008.
|
 2020, Vol. 52
2020, Vol. 52


