2. 清华大学 先进核能技术协同创新中心,北京 100084;
3. 先进反应堆工程与安全教育部重点实验室(清华大学),北京 100084
2. Collaborative Innovation Center of Advanced Nuclear Energy Technology, Tsinghua University, Beijing 100084, China;
3. Key Laboratory of Advanced Reactor Engineering and Safety (Tsinghua University), Ministry of Education, Beijing 100084, China
沸腾通道内的两相流动不稳定性可能导致有害机械振动,干扰控制系统,使部件热疲劳并恶化传热性能,因而受到广泛关注. Boure等[1]、Kakac等[2]、Ruspini等[3]基于大量的实验与理论研究对该问题进行了系统的分类.对于沸水反应堆和蒸汽发生器,尤其要注意避免在高出口干度条件下发生由摩擦压降主导的第二类密度波振荡.在临界的反应堆内中子通量密度的空间分布是不均匀的,对于动力堆中常见的圆柱形堆芯,其轴向功率服从余弦函数分布,其径向功率服从贝塞尔函数分布.尽管在实际中采取各类功率分布展平措施,其热中子通量密度分布不均匀系数仍在1.4左右[4].此外,由于各种原因,冷却剂在堆芯内数量庞大的平行通道中的流量分配并不是均匀的,通常采用增加堆芯入口流动阻力的方式展平进口流量[5].
国内外学者对这些轴向和径向上的不均匀分布进行了实验与理论研究. Dijkman等[6]、Dutta等[7]通过数值模拟研究发现轴向热流余弦分布具有强烈的稳定效应.然而,Narayanan等[8]、Lu等[9]在研究多种轴向热流分布的基础上指出轴向热流余弦分布在低入口过冷度下使系统稳定性增强,在高入口过冷度下使系统稳定性减弱.黄军等[10]、Guo等[11]对低压下平行通道系统中的流动不稳定性进行了实验研究,分析了两个通道不均匀加热和入口节流的影响;夏庚磊等[12-13]采用RELAP5程序进行数值模拟,分析了系统参数的影响. Xia等[14]研究了径向不均匀加热和入口节流对流量分配不稳定性的影响,并分析了通道压降与流量变化的关系.上述对轴向热流不均匀分布的研究所得结论尚未统一,因此有必要探究其影响流动不稳定性的机理.
本文利用RELAP5/MOD4.0程序对并联沸水堆子通道系统进行数值模拟,对比了轴向热流线性分布及余弦分布工况下的流动不稳定边界,分析了系统和通道的临界相变数随径向功率和入口节流系数不均匀性增大的变化情况,系统地研究不均匀加热与入口节流对平行通道内密度波不稳定性的影响,以期为核动力设备的设计和运行提供参考和依据.
1 研究方法 1.1 模型的建立强迫循环回路中的两个并联通道作为一种典型的边界条件被广泛应用于流动不稳定性的实验与理论研究中,其特点是平行通道的总流量保持恒定.本研究采用基于两流体、非平衡、非均相两相流模型的大型热工水力瞬态分析程序RELAP5/MOD4.0进行数值模拟.程序中采用的基本守恒方程如下.
气相和液相质量守恒方程:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{v_{\rm{g}}}A} \right) = {\mathit{\Gamma }_{\rm{g}}}, \\ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{f}}}{\rho _{\rm{f}}}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{f}}}{\rho _{\rm{f}}}{v_{\rm{f}}}A} \right) = {\mathit{\Gamma }_{\rm{f}}}. \end{array} $ |
式中:t为时间,s;α为体积分数;ρ为密度,kg/m3;A为流道横截面积,m2;x为轴向坐标,m;v为流速,m/s;Γ为传质速率,kg/(m3·s);下标g、f分别为气相液相.
气相和液相动量守恒方程:
| $ \begin{array}{l} \;\;\;\;\;\;\;{\alpha _{\rm{g}}}{\rho _{\rm{g}}}A\frac{{\partial {v_{\rm{g}}}}}{{\partial t}} + \frac{1}{2}{\alpha _{\rm{g}}}{\rho _{\rm{g}}}A\frac{{\partial {v_{\rm{g}}}^2}}{{\partial x}} = - {\alpha _{\rm{g}}}A\frac{{\partial p}}{{\partial x}} + {\alpha _{\rm{g}}}{\rho _{\rm{g}}}{B_x}A - \\ {\alpha _{\rm{g}}}{\rho _{\rm{g}}}{F_{{\rm{gW}}}}{v_{\rm{g}}}A + {\mathit{\Gamma }_{\rm{g}}}A\left( {{v_{{\rm{gl}}}} - {v_{\rm{g}}}} \right) - {\alpha _{\rm{g}}}{\rho _{\rm{g}}}{F_{{\rm{gl}}}}A\left( {{v_{\rm{g}}} - {v_{\rm{f}}}} \right) - \\ C{\alpha _{\rm{g}}}{\alpha _{\rm{f}}}{\rho _{\rm{m}}}A\left[ {\frac{{\partial \left( {{v_{\rm{g}}} - {v_{\rm{f}}}} \right)}}{{\partial t}} + {v_{\rm{f}}}\frac{{\partial {v_{\rm{f}}}}}{{\partial x}}} \right], \\ \;\;\;\;\;\;\;{\alpha _{\rm{f}}}{\rho _{\rm{f}}}A\frac{{\partial {v_{\rm{f}}}}}{{\partial t}} + \frac{1}{2}{\alpha _{\rm{f}}}{\rho _{\rm{f}}}A\frac{{\partial {v_{\rm{f}}}^2}}{{\partial x}} = - {\alpha _{\rm{f}}}A\frac{{\partial p}}{{\partial x}} + {\alpha _{\rm{f}}}{\rho _{\rm{f}}}{B_x}A - \\ {\alpha _{\rm{f}}}{\rho _{\rm{f}}}{F_{{\rm{fW}}}}{v_{\rm{f}}}A + {\mathit{\Gamma }_{\rm{f}}}A\left( {{v_{{\rm{fl}}}} - {v_{\rm{f}}}} \right) - {\alpha _{\rm{f}}}{\rho _{\rm{f}}}{F_{{\rm{fl}}}}A\left( {{v_{\rm{f}}} - {v_{\rm{g}}}} \right) - \\ C{\alpha _{\rm{f}}}{\alpha _{\rm{g}}}{\rho _{\rm{m}}}A\left[ {\frac{{\partial \left( {{v_{\rm{f}}} - {v_{\rm{g}}}} \right)}}{{\partial t}} + {v_{\rm{g}}}\frac{{\partial {v_{\rm{g}}}}}{{\partial x}}} \right]. \end{array} $ |
式中:p为压力,Pa;B为质量力,m/s2;FgW和FfW为气和液相壁面曳力系数,s-1;vgI和vfI为相界面处气和液相流速,m/s;FgI和FfI为气和液相相界面曳力系数,s-1;C为虚拟质量系数.
气相和液相能量守恒方程:
| $ \begin{array}{l} \;\;\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{U_{\rm{g}}}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{U_{\rm{g}}}{v_{\rm{g}}}A} \right) = - p\frac{{\partial {\alpha _{\rm{g}}}}}{{\partial t}} - \\ \frac{p}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{g}}}{v_{\rm{g}}}A} \right)\mathit{ + }{\mathit{q}_{{\rm{wg}}}}\mathit{ + }{\mathit{q}_{{\rm{ig}}}}\mathit{ + }{\mathit{\Gamma }_{{\rm{ig}}}}h_{\rm{g}}^* + {\mathit{\Gamma }_{\rm{w}}}{h_{\rm{g}}} + {\mathit{\Phi }_{\rm{g}}}, \\ \;\;\;\;\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{f}}}{\rho _{\rm{f}}}{U_{\rm{f}}}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{f}}}{\rho _{\rm{f}}}{U_{\rm{f}}}{v_{\rm{f}}}A} \right) = - p\frac{{\partial {\alpha _{\rm{f}}}}}{{\partial t}} - \\ \frac{p}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _{\rm{f}}}{v_{\rm{f}}}A} \right)\mathit{ + }{\mathit{q}_{{\rm{wf}}}}\mathit{ + }{\mathit{q}_{{\rm{if}}}}\mathit{ + }{\mathit{\Gamma }_{{\rm{if}}}}h_{\rm{f}}^* + {\mathit{\Gamma }_{\rm{w}}}{h_{\rm{f}}} + {\mathit{\Phi }_{\rm{f}}}. \end{array} $ |
式中:U为比内能,J/kg;q为体积释热率,W/m3;h为焓值,J/kg;Φ为能量耗散项,W/m3.
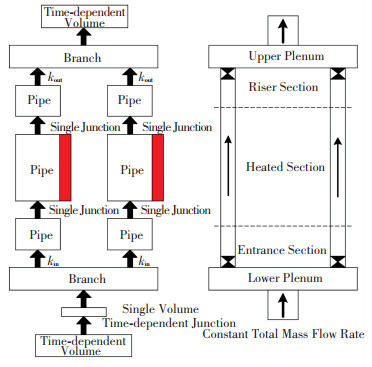
根据Guo等[11]研究中的实验装置建立的系统节点图如图 1所示.
|
图 1 RELAP5程序节点图 Fig. 1 RELAP5 nodalization |
两个几何结构相同的圆形截面竖直通道均由入口段、加热段和上升段组成,过冷水从系统底部进入,在向上流动的过程中发生相变,并以一定干度的气液两相混合物的状态流出.采用3个由单一接管部件(Single Junction)连接的管型部件(Pipe)模拟每个通道,加热功率通过内部产生热量的热构件(Heat Structure)控制,采用对流边界条件使热量从热构件传至通道内流体;分支部件(Branch)用于模拟上下两个联箱,与通道相连处设置了流动损失系数以模拟进出口节流阀的作用;时间相关控制体部件(Time-dependent Volume)用于给定入口流体的物性以及出口压力;时间相关接管部件(Time-dependent Junction)用于给定系统的入口总质量流量.经过节点敏感性分析,综合考虑计算精度与耗时,将入口段、加热段和上升段分别划分为20、50和10个控制体.
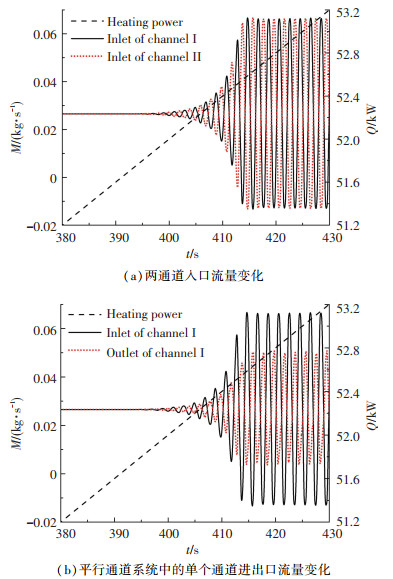
1.2 流动不稳定的判断本研究采用固定入口总质量流量同时线性增大加热功率的方式使流量发生振荡,初始时保持较大的功率增长速度以迅速接近流动不稳定边界,之后采用较小的功率增长速度以利于对流动不稳定起始的判定.经验证,这种方式与阶跃增大加热功率的方式所得流动不稳定边界相同.典型的加热功率及通道进出口质量流量变化如图 2所示.
|
图 2 平行通道流动不稳定性 Fig. 2 Flow instability in parallel channels |
系统压力2 MPa,入口温度168 ℃,入口总质量流量0.053 kg/s,两通道入口节流系数均为37.由于两个通道特性相同,功率较低时通道内处于相同质量流量的稳定流动状态,随加热功率增大,两通道入口流量发生等振幅反相振荡,振幅逐渐增大而周期保持不变,在振荡充分发展后通道的入口发生倒流,不利于核动力装置的安全可靠运行.由图 2(b)可知平行通道系统中的单个通道的进出口流量反向振荡且出口流量的振幅较小.此外,发生不稳定时通道出口处干度约为0.4.结合以上特征可知, 通道内发生了第二类密度波振荡.参照文献[11],本研究选取单个通道入口质量流量相对振幅达到10%作为判断流动不稳定发生的临界值.
1.3 模拟与实验数据的验证本研究采用Ishii等[15]提出的无量纲数表示流动不稳定边界,相变数Npch表征出口流体的相变程度,过冷度数Nsub表征入口流体的过冷度,且
| $ {N_{{\rm{pch}}}} = \frac{Q}{{M{h_{{\rm{fg}}}}}}\frac{{{\nu _{{\rm{fg}}}}}}{{{\nu _{\rm{f}}}}}, {N_{{\rm{sub}}}} = \frac{{{h_{\rm{f}}} - {h_{{\rm{in}}}}}}{{{h_{{\rm{fg}}}}}}\frac{{{\nu _{{\rm{fg}}}}}}{{{\nu _{\rm{f}}}}}. $ |
出口定干度线有助于确定系统的运行特性
| $ {N_{{\rm{sub}}}} = {N_{{\rm{pch}}}} - {x_{\rm{e}}}{\nu _{{\rm{fg}}}}/{\nu _{\rm{f}}}. $ |
式中:Q为加热功率,kW;M为质量流量,kg/s;hfg为汽化潜热,kJ/kg;νfg为饱和气液比容差,m3/kg;νf为饱和液相比容,m3/kg;hf为饱和液相焓,kJ/kg;hin为入口流体焓,kJ/kg;xe为出口热平衡含气率.
从可靠性及数值稳定性的角度出发[16],本研究选取了RELAP5/MOD4.0程序中的非平衡非均相模型和半隐式数值格式对Guo等[11]研究中的16组实验进行数值模拟,计算结果与实验结果的对比如图 3所示.

|
图 3 计算结果与实验结果的对比 Fig. 3 Comparison of computational results and experimental data |
由图 3可知,不同压力下的流动不稳定边界分布在一个条形区域内,左侧为流动稳定区间,右侧为流动不稳定区间.大多数计算结果中的临界加热功率略小于实验,相对误差在-0.9%~-14.1%,验证了模拟的准确性,也证实了RELAP5/MOD4.0程序模拟平行通道内密度波不稳定性的有效性与适用性.
2 计算结果与分析本文以典型的内部流体竖直向上流动的沸水堆子通道[16]作为研究对象,用两个并联的通道代表沸水堆堆芯数量庞大的平行通道,对轴向、径向不均匀加热以及入口节流工况下的平行通道密度波不稳定性进行研究.其中单个通道的直径为0.012 4 m,长度为3.657 6 m,壁面粗糙度为0.000 025 m,入口阻力系数变化范围为0~46,出口阻力系数为5.系统压力为7 MPa,并设置系统的总质量流量为0.264 kg·s-1.此物理模型不含绝热的入口段和上升段,经过节点敏感性分析,将单个受热通道划分为48个控制体.
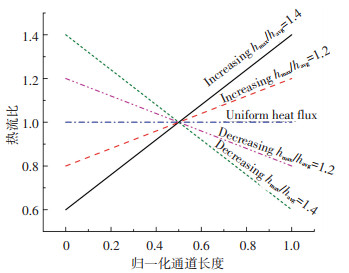
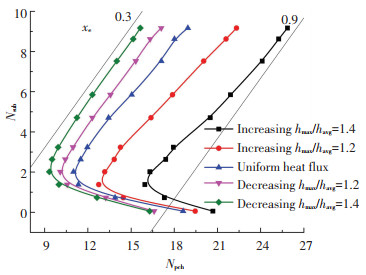
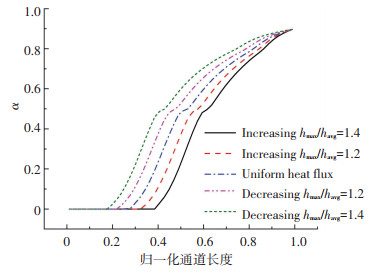
2.1 轴向不均匀加热首先对轴向加热功率线性变化的工况进行研究,以确定轴向热流不均匀分布影响流动不稳定性的机理.如图 4所示,设置了4组线性增大和减小的轴向热流密度分布,其最大热流与平均热流的比值分别为1.4和1.2.线性增大加热功率使流量发生振荡,流动不稳定起始过程中两通道入口流量随时间的变化与均匀热流工况类似,得到的流动不稳定边界如图 5所示,其中轴向热流均匀分布的结果作为对比.在不同入口过冷度下,轴向热流线性增大使系统稳定性增强而轴向热流线性减小使系统稳定性减弱.随轴向热流分布斜率逐渐增大,流动不稳定边界对应的出口热平衡含气率从不到0.3逐渐增大到超过0.9,系统稳定性得到了显著提升.其根本原因是轴向热流不均匀分布会影响沸腾边界的位置,改变单相段及两相段长度,进而改变单相段压降占通道总压降的份额. 图 6为入口温度210 ℃对应过冷度数4.706,加热功率115 kW时的空泡份额沿通道高度的分布,显然单相段长度随轴向热流分布斜率的增大而增大.由于总加热功率一定,不同轴向热流分布工况下的出口空泡份额相同.此外,由图 5可得轴向热流不均匀分布对流动不稳定的影响随入口过冷度的增大而增大.这是因为计算中沸腾边界均位于通道的前半部分,且随入口过冷度增大不断向通道出口移动,使不同轴向热流分布下从通道入口到沸腾边界的热流密度积分差异增大.
|
图 4 轴向热流线性分布 Fig. 4 Linear distribution of axial heat flux |
|
图 5 轴向热流线性分布对应流动不稳定边界 Fig. 5 Flow instability boundaries obtained from linear distribution of axial heat flux |
|
图 6 相同功率时空泡份额沿通道的分布 Fig. 6 Void fraction along the channel at same heating power |
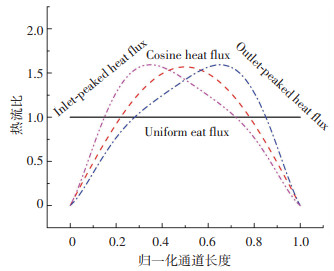
未受扰动的均匀堆芯的轴向功率服从余弦函数分布,对于实际反应堆中堆芯寿期的不同阶段,由于控制棒插入的深度不同,功率的峰值可能增大并向堆芯的顶部或底部偏移.这3种情况下的轴向热流密度分布如图 7所示,其中峰值偏向入口和出口的热流密度分布在Leung等[17]研究的基础上修改得到. 3种工况所得流动不稳定边界与均匀热流工况的对比如图 8所示.在不同入口过冷度下,轴向热流余弦分布对应临界出口热平衡含气率均大于均匀加热,系统稳定性增强.峰值偏向通道入口和出口的热流分布所对应流动不稳定边界分别处于余弦分布的两侧,因此与轴向热流余弦分布相比,峰值偏向入口会降低系统稳定性而峰值偏向出口会提高系统稳定性,这对指导反应堆的安全稳定运行具有重要意义.此外,与热流均匀分布相比,峰值偏向入口的分布在较低入口过冷度时增大系统的稳定性,在较高入口过冷度时降低系统的稳定性.
|
图 7 轴向热流余弦及峰值偏向入口及出口的分布 Fig. 7 Cosine, inlet-peaked and outlet-peaked axial heat flux distribution |
|
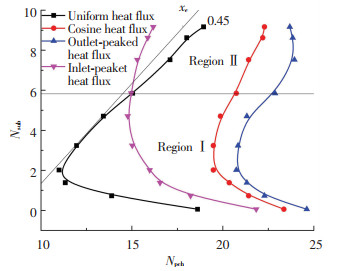
图 8 轴向热流余弦及峰值偏离中心的分布对应流动不稳定边界 Fig. 8 Flow instability boundaries obtained from cosine and peaked axial heat flux distribution |
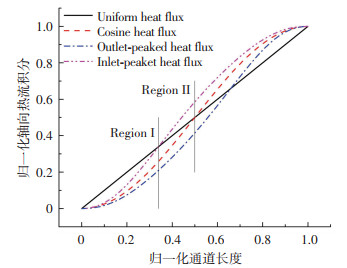
从入口到通道不同位置处的归一化热流积分如图 9所示.在整个通道长度上,热流分布的峰值越靠近通道出口,则积分热流越小,功率相同时的单相段越长,所占通道总压降份额越大,因此系统越稳定.本文不同入口过冷度下的沸腾边界都位于通道的前半部分,此时余弦分布的积分热流小于均匀分布,因此余弦加热的稳定性比均匀加热更好.此外,在图 8中以均匀与峰值偏向入口热流分布所得流动不稳定边界的交点作为入口过冷度高低的分界,并在图 9中以这两种分布对应积分热流的交点将前一半通道分成两个区间.入口过冷度较低时,沸腾边界处于区间Ⅰ,入口过冷度较高时,沸腾边界处于区间Ⅱ,积分热流曲线可以很好地解释不同流动不稳定边界的相对位置.
|
图 9 积分热流沿通道长度的分布 Fig. 9 Distribution of integral heat flux along the channel |
在Narayanan等[8]、Lu等[9]的研究中,热流余弦分布在高入口过冷度下使系统稳定性减弱,这一结果与本文并不矛盾.若沸腾边界位于通道上半部分,此时余弦分布的积分热流大于均匀分布,导致系统稳定性减弱.因此轴向热流不均匀分布时系统的稳定性取决于沸腾边界的位置以及积分热流沿通道的分布.在密度波振荡边界处,单相段与两相段的质量流量和压降存在相位差,单相段越长进而其压降占通道总压降的份额越大,使两相段的压降振幅不能平衡较大的单相段压降振幅,导致流量振荡的衰减,系统稳定性增强.
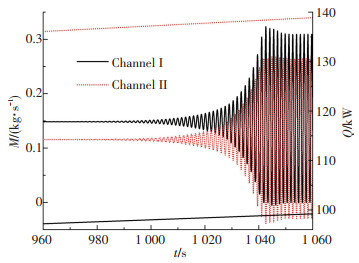
2.2 径向不均匀加热在通道轴向热流均匀分布的基础上,保持通道二的功率为通道一的1.4倍,两通道入口流量随加热功率的变化如图 10所示(入口温度255 ℃,对应过冷度数2.015).加热功率较低时两通道内处于不同流量的稳定流动状态.因为加热功率较大的通道内沸腾更加剧烈,在并联通道压降相同的条件下,对应流量较小,即两个通道内的流量不均匀分配.随加热功率线性增大,两个通道内流体同时发生反相振荡,形成密度波流动不稳定.
|
图 10 径向不均匀加热时两通道入口流量变化 Fig. 10 Variation of inlet mass flow rates under nonuniform radial heating |
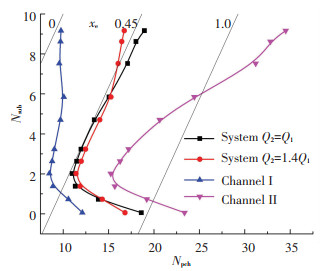
通道二功率为通道一的1.4倍时的流动不稳定边界如图 11所示,其中系统的临界相变数用发生不稳定时的总功率和流量计算,两个通道的临界相变数分别用发生不稳定时各自的功率和流量计算.还给出了两通道功率相同时的流动不稳定边界以便对比分析,此边界同时表征了系统和单个通道的稳定性.由图 11可知,两通道功率不同时系统的流动不稳定边界与功率相同时较为接近,说明径向功率不均匀分布对系统稳定性的影响并不显著.加热功率较小的通道所对应临界相变数较小而加热功率较大的通道所对应临界相变数较大,其原因是流量的不均匀分配.显然,系统的不稳定由加热功率较大的通道导致.在一些入口过冷度下功率较大的通道出口产生过热蒸汽,可能发生换热恶化甚至导致通道烧毁,应尽量避免此情况发生.
|
图 11 径向不均匀加热对应流动不稳定边界 Fig. 11 Flow instability boundaries under nonuniform radial heating |
系统及通道的临界相变数随两通道功率比的变化如图 12所示(入口温度210 ℃,对应过冷度数4.706).由图 12可知,两个通道内的稳定性差异随不均匀性增大而增大,系统的临界相变数随功率比变化不明显,说明径向功率不均匀分布对系统的稳定性影响较小.其原因可能是并联通道中和了两个通道的差异,综合了系统参数.径向功率不均匀分布引起的流量不均匀分配及传热恶化问题比流动不稳定性更值得关注.

|
图 12 径向加热不均匀性对系统和通道稳定性的影响 Fig. 12 Effect of nonuniformity of radial heating on stability of system and each channel |
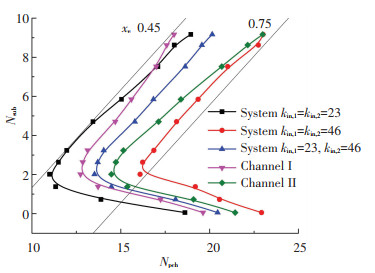
当两个通道入口节流系数不同时,也会发生类似图 10中的流量不均匀分配情况.节流系数较大的通道内流量较小而节流系数较小的通道内流量较大以保证并联通道两端压降相同.将两个通道的入口节流系数分别设置为23和46,所得系统及通道的流动不稳定边界与两种入口节流系数相等工况的对比如图 13所示. 不均匀节流时系统稳定性好于较小入口节流系数的均匀节流(kin, 1=kin, 2=23),差于对应较大入口节流系数的均匀节流(kin, 1=kin, 2=46).入口节流系数较小的通道稳定性相对均匀节流(kin, 1=kin, 2=23)增强,而入口节流系数较大的通道稳定性相对均匀节流(kin, 1=kin, 2=46)减弱.显然,系统的不稳定由入口节流系数较小的通道导致.
|
图 13 径向不均匀入口节流对应流动不稳定边界 Fig. 13 Flow instability boundaries under nonuniform radial inlet throttling |
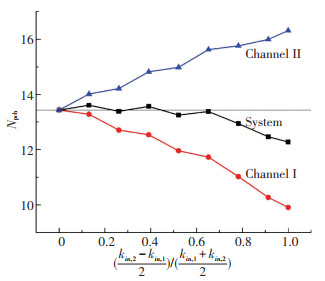
为研究入口节流不均匀性的影响,设置两通道入口节流系数之和为46,减小通道一的节流系数同时增大通道二的节流系数,所得流动不稳定的临界相变数如图 14所示(入口温度210 ℃,对应过冷度数4.706).两通道的稳定性差异随入口节流不均匀性的增大而增大.系统的稳定性介于两者之间,当不均匀性较小时,系统稳定性基本不发生变化,当不均匀性较大时,系统稳定性有减小的趋势,此结果与文献[18]中的结论相符.这是因为不均匀性较大时,改变相同大小的入口节流系数对两个通道的相对影响不同,入口节流系数较小的通道一引入的不稳定效应逐渐占据主导.
|
图 14 径向入口节流不均匀性对系统和通道稳定性的影响 Fig. 14 Effect of nonuniformity of radial inlet throttling on stability of system and each channel |
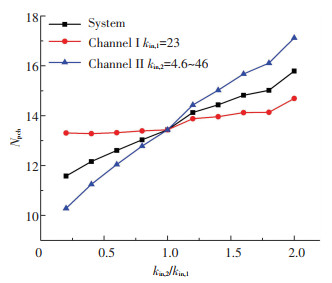
为进一步探究提高系统稳定性的方法,将通道一的入口节流系数固定为23,调节通道二的入口节流系数,所得流动不稳定的临界相变数如图 15所示(入口温度210 ℃,对应过冷度数4.706).随通道二入口节流系数增大,系统稳定性逐渐增强.其中通道二的稳定性增长较为显著,尽管通道一的入口节流系数不变,其稳定性也有较小的增长.说明增大任一通道的入口节流系数总是有利的,除自身外,其他通道与整个系统的稳定性都会增强.
|
图 15 增大单个通道的入口节流系数对系统和通道稳定性的影响 Fig. 15 Effect of increasing inlet throttling coefficient of single channel on stability of system and each channel |
1) 轴向热流不均匀分布时系统的稳定性取决于沸腾边界的位置以及积分热流沿通道的分布.
2) 与轴向热流均匀分布相比,轴向热流线性增大使系统稳定性增强而轴向热流线性减小使系统稳定性减弱;入口过冷度较低时,轴向热流余弦分布提高系统稳定性,入口过冷度较高时,系统稳定性可能增强也可能减弱.与轴向热流余弦分布相比,峰值偏向入口会降低系统稳定性; 而峰值偏向出口会提高系统稳定性.
3) 径向不均匀加热和入口节流时通道内流量发生不均匀分配,系统的流动不稳定由相对不稳定的通道即功率较大或入口节流系数较小的通道导致.
4) 径向不均匀加热对系统稳定性影响较小.对于径向不均匀入口节流,系统稳定性随不均匀性的增大有减小的趋势,可采用增大任一通道入口节流系数的方法提高系统的稳定性.
| [1] |
BOURE J A, BERGLES A E, TONG L S. Review of two-phase flow instability[J]. Nuclear Engineering and Design, 1973, 25(2): 165. DOI:10.1016/0029-5493(73)90043-5 |
| [2] |
KAKAC S, BON B. A review of two-phase flow dynamic instabilities in tube boiling systems[J]. International Journal of Heat and Mass Transfer, 2008, 51(3/4): 399. DOI:10.1016/j.ijheatmasstransfer.2007.09.026 |
| [3] |
RUSPINI L C, MARCEL C P, CLAUSSE A. Two-phase flow instabilities: a review[J]. International Journal of Heat & Mass Transfer, 2014, 71(3): 521. DOI:10.1016/j.ijheatmasstransfer.2013.12.047 |
| [4] |
谢仲生, 吴宏春, 张少泓. 核反应堆物理分析[M]. 修订本.西安: 西安交通大学出版社, 2014: 110.
|
| [5] |
于平安, 朱瑞安, 喻真烷, 等. 核反应堆热工分析[M]. 第3版. 上海: 上海交通大学出版社, 2002: 145.
|
| [6] |
DIJKMAN F J M, SLUITER M L C. One-channel non-linear digital model for boiling water hydrodynamics[J]. Nuclear Engineering & Design, 1971, 16(3): 237. DOI:10.1016/0029-5493(71)90012-4 |
| [7] |
DUTTA G, DOSHI J B. A characteristics-based finite-difference scheme for the analysis of instability in water cooled reactors[J]. Nuclear Engineering and Technology, 2008, 40(6): 477. DOI:10.5516/NET.2008.40.6.477 |
| [8] |
NARAYANAN S, SRINIVAS B, PUSHPAVANAM S, et al. Non-linear dynamics of a two phase flow system in an evaporator: the effects of (i) a time varying pressure drop (ii) an axially varying heat flux[J]. Nuclear Engineering & Design, 1997, 178(3): 279. DOI:10.1016/S0029-5493(97)00233-1 |
| [9] |
LU Xiaodong, WU Yingwei, ZHOU Linglan, et al. Theoretical investigations on two-phase flow instability in parallel channels under axial non-uniform heating[J]. Annals of Nuclear Energy, 2014, 63: 75. DOI:10.1016/j.anucene.2013.07.030 |
| [10] |
黄军, 黄彦平, 王飞, 等. 不对称节流和不对称加热对平行双通道管间脉动特性影响实验[J]. 核动力工程, 2006, 27(6): 18. HUANG Jun, HUANG Yanping, WANG Fei, et al. Experiment of effect of dissymmetry throttling and heating on oscillation between double parallel channels[J]. Nuclear Power Engineering, 2006, 27(6): 18. DOI:10.3969/j.issn.0258-0926.2006.06.005 |
| [11] |
GUO Yun, HUANG Jun, XIA Genglei, et al. Experiment investigation on two-phase flow instability in a parallel twin-channel system[J]. Annals of Nuclear Energy, 2010, 37(10): 1281. DOI:10.1016/j.anucene.2010.05.021 |
| [12] |
夏庚磊, 郭赟, 彭敏俊. 基于RELAP5的两管平行通道流动不稳定性研究[J]. 原子能科学技术, 2010, 44(6): 694. XIA Genglei, GUO Yun, PENG Minjun. Investigation on two-phase flow instability in parallel channels based on relap5 code[J]. Atomic Energy Science and Technology, 2010, 44(6): 694. |
| [13] |
夏庚磊, 董化平, 彭敏俊, 等. 环隙窄缝通道管间脉动不稳定性分析[J]. 原子能科学技术, 2011, 45(9): 1034. XIA Genglei, DONG Huaping, PENG Minjun, et al. Analysis of instability in narrow annular multi-channel system[J]. Atomic Energy Science and Technology, 2011, 45(9): 1034. |
| [14] |
XIA Genglei, SU Guanghui, PENG Minjun. Analysis of flow distribution instability in parallel thin rectangular multi-channel system[J]. Nuclear Engineering and Design, 2016, 305: 604. DOI:10.1016/j.nucengdes.2016.04.016 |
| [15] |
ISHⅡ M, ZUBER N. Thermally induced flow instabilities in two phase mixtures[C]//Proceedings of the 4th International Heat Transfer Conference. Paris: Begel House Inc, 1970: 26
|
| [16] |
AMBROSINI W, FERRERI J C. Analysis of basic phenomena in boiling channel instabilities with different flow models and numerical schemes[C]//Proceedings of the 14th International Conference on Nuclear Engineering. Miami: American Society of Mechanical Engineers, 2006: 889. DOI: 10.1115/ICONE14-89863
|
| [17] |
LEUNG L K H, GROENEVELD D C. Critical heat flux in axially non-uniform-heated channels[C]//Proceedings of the 13rd International Heat Transfer Conference. Sydney: Begel House Inc., 2006. DOI: 10.1615/IHTC13.p28.50
|
| [18] |
QIAN Libo, DING Shuhua, QIU Suizheng. Research on two-phase flow instability in parallel rectangular channels[J]. Annals of Nuclear Energy, 2014, 65: 47. DOI:10.1016/j.anucene.2013.10.035 |
 2020, Vol. 52
2020, Vol. 52


