2. 上海振华重工(集团)股份有限公司, 上海 200125
2. Shanghai Zhenhua Heavy Industries Co., Ltd., Shanghai 200125, China
在港口高效自动化的发展趋势要求下, 自动化轨道式集装箱龙门起重机(ARMG)的工作效率随之提高.但某型ARMG在高速搬运重物时, 会受到大车及小车加减速影响, 使吊具和吊重大幅摆动, 导致无法精确定位, 严重降低集装箱装卸效率.另外, 对全钢结构的ARMG设备, 高速运动带来的摇摆振动很难衰减且需要起重机金属结构及其传动机构来吸收, 会影响其寿命并带来安全隐患, 因此需要对吊具采取防摇措施.传统RMG的防摇是通过小车中的司机不断操纵小车来回移动实现的, 容易使司机产生恶心等不适症状, 且防摇效率较低, 易产生安全事故.而在自动化码头中, ARMG将不再通过司机的操纵实现防摇, 同时对其工作效率和安全性的要求也越来越高, 因此为其找到合理的防摇措施十分必要.
目前, 工程中采用的防摇方法包括机械防摇和电子防摇, 机械防摇主要通过提高悬挂刚度或安装阻尼器的方法实现, 会带来较大附加质量, 不利于钢丝绳等构件的维护.雷步忠[1]发明了集装箱起重机八绳防摇起升机构; 唐凡[2]进一步对八绳起升缠绕机构中“倒三角型”和“正三角型”这两种方式的工作原理和防摇效果进行了分析和研究; 而张氢等[3]对应用八绳防摇后RTG的防摇影响因素进行了分析; 白传悦[4]对5种利用减摆装置的机械防摇方法进行了研究和分析; 洪丁节等[5]从能量角度出发改进了八绳防摇系统并提高了总体刚度.电子防摇一般通过控制小车运行来实现防摇, 但利用小车控制吊具摆动会使小车无法准确定位, 严重影响工作效率.电子防摇主要包括开环及闭环控制, 徐军等[6]对电子防摇控制中LQR最优控制、内模控制以及模糊控制这3种典型的控制理论和方法进行了分析; 吴庆祥等[7]利用输入整形控制理论, 提出了以控制负载摆幅为目标的多段匀变速前馈防摇控制算法; 郁春丽等[8]提出了正反Posicast输入整形法, 使吊重摆幅在不同系统阻尼震荡周期内归零; Kimiaghalam等[9-10]采用遗传算法研究吊重防摇的时间最优问题; 付主木等[11]提出了一种以事件驱动为切换规则的多模型参考切换双闭环防摇控制算法; Grassin等[12]采用LQR方法通过跟踪参考轨迹来实现定位和防摇控制; Liu等[13]针对双摆模型, 设计了一个自适应滑模模糊控制器用于控制两个串联摆的摆动; 肖鹏等[14]将模糊神经网络技术应用到防摇控制系统研究中, 并给出了仿真结果; 王璐等[15]在研究桥式起重机的电子防摇控制策略时, 建立了考虑驱动小车电机变频器模型的桥机系统动力学模型; Lew等[16]对吊重运动过程中质量变化情况进行了研究, 并对比例微分控制和全状态反馈的结果进行了比较.
本文提出了一种利用吊具辅助钢丝绳作牵引的主动防摇方法, 通过辅助钢丝绳对吊具施加牵引力消耗吊具的摆动动能, 从而减小吊具偏摆幅值, 不仅避免了繁重的附加防摇装置, 而且无需通过小车实现防摇减摆功能, 提高了其定位精确性, 可更理想的实现防摇目标.
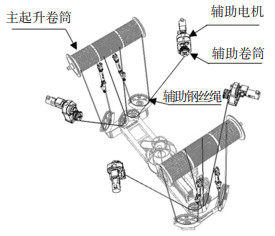
1 主动防摇方案为了实现吊具主动防摇的功能, 在ARMG吊具上添加辅助钢丝绳, 并通过图 1所示的辅助电机与卷筒牵引辅助钢丝绳, 用4个辅助电机对钢丝绳进行牵引限制吊具摆动, 实现主动防摇的功能.
|
图 1 吊具辅助钢丝绳、辅助电机及其布置方式 Fig. 1 Auxiliary wire ropes, auxiliary motors and their disposal method |
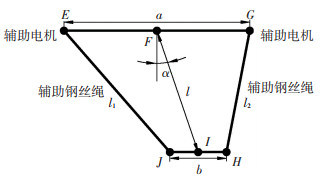
采用不同辅助电机牵引方案进行防摇控制, 可以分别实现ARMG大车和小车运动方向上的防摇目标.在实际生产作业中, 由小车运动产生的吊具摆动进行防摇的需求较大, 而且要求较高, 因此本文将从该方向对主动防摇方法进行介绍.如图 2为吊具与辅助钢丝绳以及辅助电机之间的位置关系, E、G分别为辅助电机位置, J、H为辅助钢丝绳在吊具上的连接位置, l为小车中点到吊具中点的距离, l1、l2为辅助钢丝绳绳长, a为辅助钢丝绳在小车上连接点之间的距离, b为辅助钢丝绳在吊具上连接点之间的距离, α为摆动产生的夹角.
|
图 2 吊具与辅助钢丝绳、辅助电机之间的位置关系 Fig. 2 Positional relationship between spreader, auxiliary wire ropes and auxiliary motors |
根据图 2所示的几何关系, 假设α较小, 可得
| $ l_1^2 = {l^2} + (a - b)l\alpha + \frac{{{{(a - b)}^2}}}{4}, $ | (1) |
| $ l_2^2 = {l^2} - (a - b)l\alpha + \frac{{{{(a - b)}^2}}}{4}. $ | (2) |
左右辅助钢丝绳绳长l1、l2以及夹角α将由于吊具的摆动而随时间发生变化, 因此对式(1)及式(2)对时间求导, 可得
| $ 2{l_1}{{\dot l}_1} = (a - b)l\dot \alpha , $ | (3) |
| $ 2{l_2}{{\dot l}_2} = - (a - b)l\dot \alpha . $ | (4) |
分析式(3)及式(4)可知, 当吊具如图 2所示沿逆时针方向摆动时, 左侧的辅助电机通过收缩辅助钢丝绳, 对吊具施加牵引力, 同时为了防止右侧钢丝绳收绳时发生脱绳现象, 右侧辅助电机需要施加较小的牵引力收紧钢丝绳; 当吊具沿顺时针方向摆动时, 右侧辅助电机收缩辅助钢丝绳对吊具施加牵引力, 同时左侧钢丝绳收回.根据现场装卸以及工程实际要求, 若吊具摆幅减至100 mm之内, 则表示已进入安全摆动范围, 此时可停止施加拉力.
2 主动防摇动力学建模 2.1 系统动力学方程为研究集装箱摆角响应与起重机系统的关系, 建立主动防摇系统动力学模型, 如图 3所示.主动防摇动力学模型主要由小车、起升钢丝绳及集装箱构成, α为吊具的摆角, x为吊具质心的水平位置, y为吊具质心的竖直位置, θ为吊具相对于水平位置的夹角, m为吊具总质量, α1和α2分别为图示左右起升钢丝绳与竖直方向的夹角, d为小车上左右起升滑轮间的水平距离, l为小车中点到吊具中点的距离, l0为辅助电机与吊具静止状态下的垂直距离, L1和L2为左右两边起升钢丝绳的长度, δ为辅助电机与吊具垂直距离的变化量, δ1和δ2分别为左右起升钢丝绳的伸长量, w为吊具上左右起升滑轮的距离, r为吊具高度的一半.

|
图 3 主动防摇动力学模型 Fig. 3 Dynamic model of active anti-swing |
图 3中X、Y分别表示主动防摇动力学模型水平和竖直的正方向,0表示两个方向上的零点, 同时规定转角α、α1、α2、θ逆时针转动为正, 因此由图中四边形APCQ和四边形DBPQ可知:
| $ \begin{array}{*{20}{c}} {{L_i}\sin \left( {{\alpha _i}} \right) = l\sin (\alpha ) + {{( - 1)}^i}\frac{1}{2}w\cos (\theta ) - }\\ {{{( - 1)}^i}\frac{1}{2}d,(i = 1,2);} \end{array} $ | (5) |
| $ {L_i}\cos \left( {{\alpha _i}} \right) = l\cos (\alpha ) - {( - 1)^i}\frac{1}{2}w\sin (\theta ),(i = 1,2). $ | (6) |
为了消除式(5)、(6)中的αi, 分别对两式平方后相加, 可得
| $ \begin{array}{l} L_i^2 = {\left( {l\sin (\alpha ) + {{( - 1)}^i}\frac{1}{2}w\cos (\theta ) + \frac{1}{2}d} \right)^2} + \\ \;\;\;\;\;\;\;{\left( {l\cos (\alpha ) - {{( - 1)}^i}\frac{1}{2}w\sin (\theta )} \right)^2},(i = 1,2). \end{array} $ | (7) |
若考虑钢丝绳变形, 可得
| $ {L_i} = {l_0} + {\delta _i},\;\;\;\;(i = 1,2). $ | (8) |
| $ l = {l_0} + \delta . $ | (9) |
将式(8)、(9)代入式(7)中化简可得
| $ {\delta _i} = \frac{{{w^2}{a^2}}}{{8{l_0}}} + {( - 1)^{i + 1}}\frac{w}{2}(a\alpha + \theta ) + \delta ,(i = 1,2). $ | (10) |
其中,
| $ a = (d - w)/w. $ | (11) |
根据式(10)、(11)可得吊具的动能和势能分别为
| $ {E_{\rm{K}}} = \frac{1}{2}m\left( {{{\dot x}^2} + {{\dot y}^2}} \right) + \frac{1}{2}J{{\dot \theta }^2}, $ |
| $ {E_{\rm{P}}} = mgy + \frac{1}{2}k\left( {\delta _1^2 + \delta _2^2} \right). $ |
式中:
| $ x = s + l\sin (\alpha ) + r\sin (\theta ),y = - l\cos (\alpha ) - r\cos (\theta ). $ |
图 3主动防摇动力学系统中, 广义坐标为x=[δ α θ]T, 根据拉格朗日动力学方程, 该系统的质量矩阵和刚度矩阵为
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} m&0&0\\ 0&{ml_0^2}&{mr{l_0}}\\ 0&{mr{l_0}}&{m{r^2} + J} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {2k}&0&0\\ 0&{mg{l_0} + \frac{1}{2}k{w^2}{a^2}}&{\frac{1}{2}k{w^2}a}\\ 0&{\frac{1}{2}k{w^2}a}&{mgr + \frac{1}{2}k{w^2}} \end{array}} \right]. $ |
同时, 该动力学系统中对吊具施加的外力可以表示为
| $ \mathit{\boldsymbol{f}} = {\left[ {mg - \frac{{k{w^2}{a^2}}}{{4{l_0}}} - m{l_0}\ddot s - mr\ddot s} \right]^{\rm{T}}}, $ |
于是
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{Kx}} = \mathit{\boldsymbol{f}}. $ | (12) |
结合主动防摇系统中的质量矩阵、刚度矩阵以及外力,可得其系统动力学方程为
| $ \mathit{\boldsymbol{M}}\left[ {\begin{array}{*{20}{c}} {\ddot \delta }\\ {\ddot \alpha }\\ {\ddot \theta } \end{array}} \right] + \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{l}} \delta \\ \alpha \\ \theta \end{array}} \right] = \mathit{\boldsymbol{f}}. $ | (13) |
式(13)是未考虑系统阻尼时的动力学方程, 而主动防摇是通过牵引辅助钢丝绳消耗吊具摆动动能实现的, 其效果与阻尼耗能对系统的影响相同, 因此需要在已有系统动力学方程的基础上考虑由于引入辅助钢丝绳而带来的系统阻尼, 并通过阻尼耗能等效表示牵引力的作用效果.
假设辅助钢丝绳在初始时刻与竖直方向的夹角为β, 当吊具摆动一定角度α后, 钢丝绳与竖直方向所形成的角度近似为α+β, 因此在吊具的一个摆动周期内, 牵引力F做功可以表示为
| $ {W_F} = 2 \times \int\limits_{ - {\alpha _{\max }}}^{{\alpha _{\max }}} {Fl\sin (\alpha + \beta ){\rm{d}}\alpha = 4Fl\sin \beta \sin {\alpha _{\max }}} . $ |
吊具摆动角度的变化可以表示为
| $ \alpha = {\alpha _{\max }}\sin (\omega t + \varphi ). $ |
式中:
同理, 一个周期内等效阻尼消耗的能量为
| $ {W_C} = \int\limits_0^\alpha {{c_{{\rm{eq}}}}\dot \alpha {\rm{d}}\alpha } = {c_{{\rm{eq}}}}\alpha _{\max }^2\omega ({\rm{ \mathsf{ π} }} - 2\sin (2\varphi )). $ |
因为牵引力的作用效果与阻尼耗能的效果相同, 所以钢丝绳牵引力的等效阻尼可以表示为
| $ {c_{{\rm{eq}}}} = \frac{{4Fl\sin \beta \sin {\alpha _{\max }}}}{{\alpha _{\max }^2\omega ({\rm{ \mathsf{ π} }} - 2\sin (2\varphi ))}}. $ | (14) |
若假设初相位为0, 摆幅角度较小且考虑两侧钢丝绳同时做功, 则式(14)可以简化为
| $ {c_{{\rm{eq}}}} = 8Fl\sin \beta /\left( {{\alpha _{\max }}\omega {\rm{ \mathsf{ π} }}} \right). $ | (15) |
因为牵引力做功耗能和钢丝绳阻尼耗能的效果相同, 所以利用辅助钢丝绳对吊具施加牵引力实现主动防摇的方法, 可以通过在系统中考虑阻尼等效, 因此系统的动力学方程可以由式(12)改写为
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{Kx}} + \mathit{\boldsymbol{C\dot x}} = \mathit{\boldsymbol{f}}, $ |
其中,
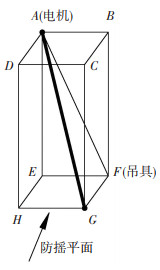
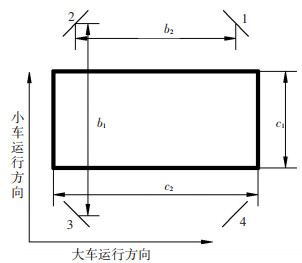
辅助钢丝绳与吊具之间会形成如图 4所示的空间关系, 前文中的牵引力F为实际牵引力在防摇平面内的分力, A为辅助钢丝绳与辅助电机的连接点, G为辅助钢丝绳与吊具的连接点, AB为辅助电机与吊具在小车行走方向的距离, AD为辅助电机与吊具在大车行走方向的距离, 平面ABFE为防摇平面, 同时根据图 5所示的辅助电机与小车的位置关系及吊具的尺寸, 可得AB=(b1-c1)/2, AD=(c2-b2)/2, 结合辅助电机与吊具在初始静止状态时的垂直距离AE=l0可知AF的长度, 即可通过余弦定理得到空间角ϕ=∠GAF, ψ=∠GAH, 以及β=∠EAF的大小.因此, 钢丝绳实际牵引力F1与其在防摇平面内的分力F之间的关系为F=F1cos ϕ, 同时若将单摆频率代替角频率, 式(15)可以简化为
|
图 4 辅助钢丝绳与吊具的空间关系 Fig. 4 Special relationship between the auxiliary wire ropes and the spreader |
|
图 5 辅助电机与小车的位置关系 Fig. 5 Position relationship between auxiliary motors and the trolley |
| $ {c_{{\rm{eq}}}} = \frac{{8{F_1}{l_0}\cos \phi \sin \beta }}{{{\alpha _{\max }}\omega {\rm{ \mathsf{ π} }}}} = \frac{{0.85{F_1}l_0^{1.5}\cos \phi \sin \beta }}{{{\alpha _{\max }}}}. $ |
由此可得辅助钢丝绳牵引力的表达式为
| $ {F_1} = = \frac{{0.07c}}{{{b_1} - {c_1}}}\sqrt {\frac{{4l_0^2 + {{\left( {{b_1} - {c_1}} \right)}^2} + {{\left( {{b_2} - {c_2}} \right)}^2}}}{{l_0^3}}} . $ | (16) |
根据经验, 影响集装箱摆动状态的主要因素有集装箱的质量m、辅助电机与吊具在静止状态时的垂直距离l0和小车行驶加速度a.为简化防摇因素, 加速度默认取最大值, 因此在后续分析中假设等效阻尼只与电机和吊具之间的垂直距离及质量有关, 各变量的数学关系可通过对吊重在不同高度下的动力学仿真以及线性拟合的方法得到.若要保证小车停止后吊具的摆幅幅值可以在2.5个周期内减少至100 mm之内这一防摇要求, 根据多次仿真结果分析, 各参数之间的关系应为
| $ {c_{{\rm{eq}}}} = 6m\left( {{l_0} - 2} \right). $ | (17) |
由式(17)可得一定工况下使吊具摆幅按防摇要求衰减的等效阻尼的大小, 并可通过式(16)获得实际辅助钢丝绳的牵引力大小.
3 仿真与实验验证 3.1 仿真由设定小车运行参数和起吊结构参数来确定不同起吊方案, 在计算机中建立主动防摇系统动力学模型并针对不同的起吊方案分别进行主动防摇下吊具的摆动响应仿真, 观察主动防摇效果.
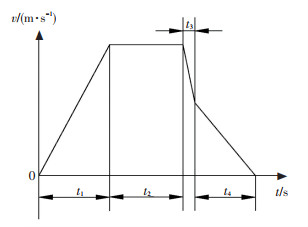
设定小车加速度为0.3m/s2, 最大速度为1.2 m/s, 减速时间为4 s且匀速运行时间≤2 s, 可得如图 6所示的小车运行速度曲线, 并可按表 1所示设计3组小车运行方案.
|
图 6 小车运行速度曲线 Fig. 6 Running speed curve of trolley |
| 表 1 3种小车运行方案 Tab. 1 Three kinds of car running scheme |
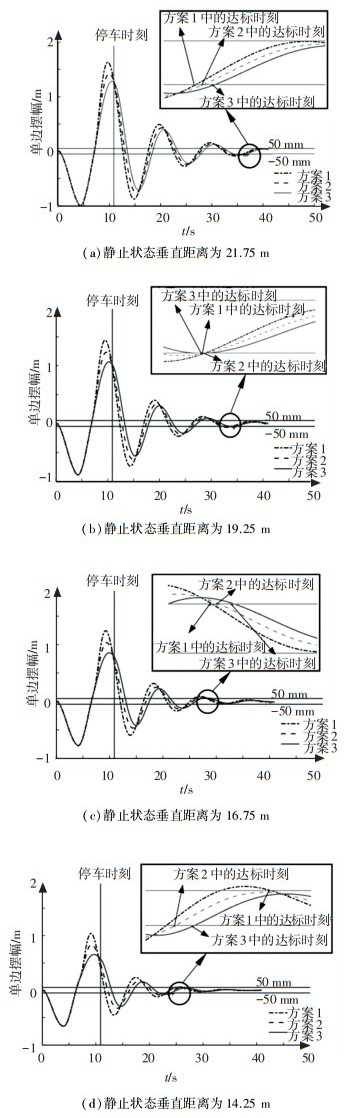
根据ARMG工作堆叠箱数、集装箱高度、最大起吊高度以及在最大起吊高度时钢丝绳伸长量, 确定了4种吊具典型垂荡高度, 并依此得到了对应的4组辅助电机与吊具在静止状态时的垂直距离, 分别是14.25、16.75、19.25和21.75 m, 并假设在这4组不同绳长下吊具质量均为40 t, 依此确定4组起吊结构方案.根据4组起吊结构方案以及3组小车运行方案, 结合在计算机中建立的考虑等效阻尼的主动防摇力学模型进行吊具的摆幅响应仿真, 得到图 7所示在不同起吊结构参数下不同小车运行参数时的摆幅响应.将吊具朝小车前进方向的摆动定义为响应中的正方向.
|
图 7 不同运行参数下的摆幅大小 Fig. 7 Swing responses of different operating parameters |
根据图 7仿真结果, 可得在第2.5个周期时不同起吊结构参数下不同小车运行参数时的摆幅大小以及在不同参数方案下辅助钢丝绳的牵引力大小见表 2.
| 表 2 不同方案下的摆幅大小以及辅助钢丝绳牵引力大小 Tab. 2 Swing responses and the forces of auxiliary wire ropes under different parameters |
由图 7和表 2可知, 在不同方案下使用主动防摇方法后均可满足在小车停车后的2.5个周期内吊具摆幅范围减少到100 mm之内, 符合安全标准, 说明防摇的主要影响因素选取正确, 且等效阻尼与辅助电机和吊具在静止状态时的垂直距离以及吊具质量之间的关系表达式拟合合理, 证明了文中提出的防摇策略在理论上是正确可行的, 可实现防摇要求.
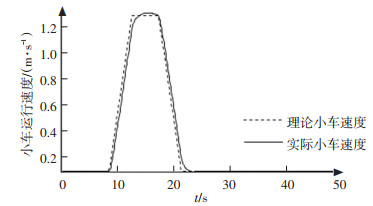
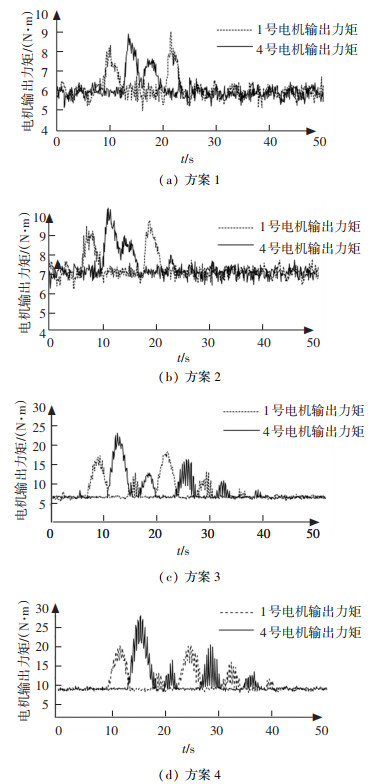
3.2 试验为验证上述基于等效阻尼的主动防摇控制算法的准确性和有效性, 以最大起升质量为40 t的某型ARMG作为实验机进行了防摇试验.试验过程中, 通过对驱动器测量求取4个辅助电机输出力矩的变化, 并通过安装在输出轴端处的增量式编码器测量各辅助电机输出角速度和转向.考虑到电机布置的对称性, 这里仅分析1号和4号辅助电机的输出力矩.在表 3的4组试验方案中, 在不同吊具质量下选择辅助电机与吊具在初始静止状态时的垂直距离为14.25, 16.75 m的两种典型垂荡高度作为试验起吊高度, 且小车按如图 8所示的速度方案在4组不同的试验方案下运行, 分别获得了如图 9所示的4组1号和4号辅助电机的输出力矩变化曲线.
| 表 3 试验方案 Tab. 3 Experimental scheme |
|
图 8 小车运行速度方案 Fig. 8 Trolly running speed scheme |
|
图 9 各组实验方案下辅助电机输出力矩曲线 Fig. 9 Output torque curves of the auxiliary motors under each experimental scheme |
由图 9可看出, 若以一侧辅助电机连续产生一次较大力矩和一次较小力矩为一个周期, 在小车运行停止后的2.5个周期内, 各实验组中的辅助电机输出力矩均变化至0附近, 说明此时集装箱摆幅已经减至安全摆动范围之内, 效果与仿真结果一致, 验证了仿真的合理性.试验过程中吊具的摇摆现象在辅助钢丝绳的牵引作用下得到了有效抑制, 高效地实现了防摇目标, 说明本文的防摇策略切实有效, 针对主动防摇动力学模型及牵引力等效阻尼的分析是正确的, 该主动防摇方法能够有效提高ARMG的工作效率.
4 结论1) 提出了一种利用辅助钢丝绳做牵引的主动防摇方法, 通过辅助钢丝绳对吊具施加牵引力从而抑制吊具摆动, 消除其摆动动能, 在ARMG工作全过程中将吊具摆动幅度抑制在安全范围内, 实现防摇目标.
2) 利用拉格朗日动力学方程建立主动防摇动力学模型, 该模型较准确地描述了ARMG吊具摆动及防摇过程, 系统阻尼的计算结果可以较准确地等效为辅助钢丝绳牵引力的大小.
3) 通过仿真和试验, 验证了不同钢丝绳分别施加牵引力抑制吊具摇摆的防摇策略的有效性, 采取该防摇策略, 在ARMG小车停止后2.5个周期内, 实现了吊具摆幅减至安全摆动范围这一目标.
4) 测试试验中, 采用本文主动防摇方法后,最大起升质量为40 t的某型ARMG较好地实现了集装箱自动化码头中的防摇目标, 并提升了ARMG的工作效率和安全性, 验证了该方法在工程中的实用性.
| [1] |
雷步忠.集装箱起重机八绳防摇起升机构: 200620124427.3[P]. 2007-07-04 LEI Buzhong. Eight rope anti swing lifting mechanism for container crane: 200620124427.3[P]. 2007-07-04 (in Chinese) |
| [2] |
唐凡. 集装箱吊具两种八绳防摇系统的比较研究[J]. 科技信息, 2012(19): 103. TANG Fan. Comparative study of two kinds of eight rope anti sway system for container spreader[J]. Science & Technology Information, 2012(19): 103. DOI:10.3969/j.issn.1673-1328.2012.19.114 |
| [3] |
张氢, 李强, 陈淼, 等. RTG八绳防摇的防摇影响因素分析及其动力学仿真[J]. 机械设计与研究, 2018, 34(2): 57. ZHANG Qing, LI Qiang, CHEN Miao, et al. Influence factors analysis and dynamic simulation of anti swing of RTG eight ropes[J]. Machine Design & Research, 2018, 34(2): 57. |
| [4] |
白传悦. 岸边集装箱起重机吊具减摆装置[J]. 起重运输机械, 2005(8): 23. BAI Chuanyue. Shimmy device for sling of quayside container crane[J]. Hoisting and Conveying, 2005(8): 23. DOI:10.3969/j.issn.1001-0785.2005.08.007 |
| [5] |
洪丁节, 冯俊华, 梁庆华. 大型岸边集装箱主动防摇策略及仿真[J]. 机械设计与研究, 2017, 33(1): 152. HONG Dingjie, FENG Junhua, LIANG Qinghua. Active anti rolling strategy and simulation of large shore container[J]. Machine Design & Research, 2017, 33(1): 152. DOI:10.13952/j.cnki.jofmdr.2017.0033(inChinese) |
| [6] |
徐军, 汪伟刚. 起重机防摇控制研究综述[J]. 造船技术, 2013(2): 25. XU Jun, WANG Weigang. The research summary on anti-swing control of crane[J]. Computer Simulation, 2013(2): 25. DOI:10.3969/j.issn.1000-3878.2013.02.008 |
| [7] |
吴庆祥, 汪小凯, 王孝文, 等. 起重机前馈防摇控制算法仿真及实验研究[J]. 武汉理工大学学报, 2016, 38(6): 109. WU Qingxiang, WANG Xiaokai, WANG Xiaowen, et al. Simulation and experimental study of feedforward and anti swing control algorithm for cranes[J]. Journal of Wuhan University of Technology, 2016, 38(6): 109. DOI:10.3963/j.issn.1671-4431.2016.06.018(inChinese) |
| [8] |
郁春丽, 牛王强. 基于输入整形法的码头装卸起重机防摇研究[J]. 计算机仿真, 2016, 33(11): 233. YU Chunli, NIU Wangqiang. Research on anti swing of dock crane based on input shaping method[J]. Computer Simulation, 2016, 33(11): 233. DOI:10.3969/j.issn.1006-9348.2016.11.051(inChinese) |
| [9] |
KIMIAGHALAM B, HOMAIFAR A, BIKDASH M. Using genetic algorithm for optimal crane control[C]// NASA URC Conference. Huntsville: NASA, 1998
|
| [10] |
KIMIAGHALAM B, HOMAIFAR A, BIKDASH M, et al. Genetic algorithms solution for unconstrained optimal crane control[C]// Proceedings of the Congress on Evolutionary Computation. Washington, D.C.: IEEE, 1999
|
| [11] |
付主木, 高爱云, 费树岷, 等. 集装箱桥吊多模型参考切换双闭环防摇控制[J]. 机械工程学报, 2011, 47(23): 161. FU Zhumu, GAO Aiyun, FEI Shumin, et al. Multiple closed loop anti swing control for container crane with multi model reference switching[J]. Journal of Mechanical Engineering, 2011, 47(23): 161. DOI:10.3901/JME.2011.23.161(inChinese) |
| [12] |
GRASSIN N, RETZ T, CARON B, et al. Robust control of a travelling crane[C]//Proceedings of the 1st European Control Conference. Paris: IEEE, 1991
|
| [13] |
LIU D, GUO W, YI J, et al. Double-pendulum-type overhead crane dynamics and its adaptive sliding mode fuzzy control[C]//Proceedings of 2004 International Conference on Machine Learning and Cybernetics. Shanghai: IEEE, 2004
|
| [14] |
肖鹏, 王冰. 模糊神经网络技术在防摇控制系统中的研究与应用[J]. 机械制造, 2005(2): 16. XIAO Peng, WANG Bing. Research and application of fuzzy neural network technology in anti shake control system[J]. Machinery, 2005(2): 16. DOI:10.3969/j.issn.1000-4998.2005.02.004(inChinese) |
| [15] |
王璐, 常中龙, 袁哲, 等. 桥式起重机防摇控制系统数学建模方法研究[J]. 起重运输机械, 2016(9): 1. WANG Lu, CHANG Zhonglong, YUAN Zhe, et al. Research on mathematical modeling method for anti-sway control system of bridge crane[J]. Hoisting and Conveying, 2016(9): 1. DOI:10.3969/j.issn.1001-0785.2016.09.001(inChinese) |
| [16] |
LEW J Y, HALDER B. Experimental study of anti-swing crane control for a varying load[C]// Proceedings of the 2003 American Control Conference. Washington D.C.: IEEE, 2003
|
 2020, Vol. 52
2020, Vol. 52


