2. 布伦瑞克工业大学 动力学与振动研究所, 布伦瑞克 38106
2. Institute of Dynamics and Vibrations, Technische Universität Braunschweig, Braunschweig 38106, Germany
土方机械与其他采用静液压传动的设备相比,具有工况复杂多变、载荷变化频繁且剧烈,对传动系统性能要求较高的特点[1].轮式装载机作为土方机械的一种常见设备,被广泛应用于建筑、矿山等多个领域,在实际应用中,装载机零部件尤其是传动系零部件故障率高,损坏严重[2-3].傅里叶变换作为常用的信号处理方法,适用于平稳信号处理,对非平稳随机载荷不能获得在某一时刻信号特征,不适用于土方机械载荷谱的处理[4-5].传统计数法编制的载荷谱多用于零部件的疲劳寿命试验,无法在时间历程上反映土方机械在作业时的非平稳随机载荷特征,该类型载荷谱不能作为提高传动零部件寿命的有效加载信号[6]. Wei等[7]、Zhang等[8]以及王健等[9]采用雨流计数法分别对装载机和挖掘机传动系统中轮齿进行疲劳寿命试验,未反映出时间历程载荷谱特征信息.土方机械传动系统复杂的扭矩变化是限制其典型作业工况构建的重要因素[10-11].为降低研发成本和缩短新产品开发周期,对传动系统的性能测试多在试验台测试或进行计算机虚拟仿真,但加载信号对测试的结果有很大影响[12].由于铲装过程中作业方式改变,频繁换挡,即使在同一作业工况下工作,不同作业段之间的载荷也会有很大差别,传动系统表现出复杂的随机行为.
本文以装载机典型换挡工况中变速器传动轴为研究对象,提出一种参数化试验载荷模型.基于小波变换级数分解的方法,将变速器传动轴所受非平稳随机载荷数据分解为非平稳的确定性分量与平稳的随机性分量,并进行参数化表达与构建.通过载荷模型随机生成的仿真载荷数据与试验测试数据的对比,验证了该方法的有效性.
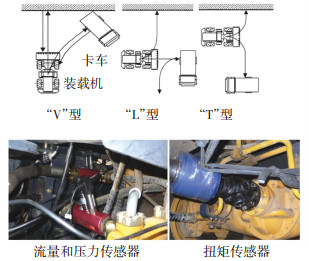
1 典型换挡工况特征及载荷谱 1.1 现场试验为构建换挡过程载荷函数,需要准确获取各工况条件下的载荷实测数据,本文以ZL50装载机进行整机现场测试,碎石中夹杂少量松散土作为作业对象,在平整的场地进行V型、L型、T型及多个满载单一换挡动作工况操作.主要的测试用元件有INDAM36数据采集仪、Barksdale流量和压力传感器、MPS-S-MA位移传感器、霍尔转速传感器以及HX902扭矩传感器等,部分工况及传感器安装图如图 1所示.在处理零值误差和满足香农采样定理等相同测试条件下进行多次试验,获得若干测试样本.
|
图 1 典型工况及部分传感器安装图 Fig. 1 Typical working conditions and some sensor installation drawings |
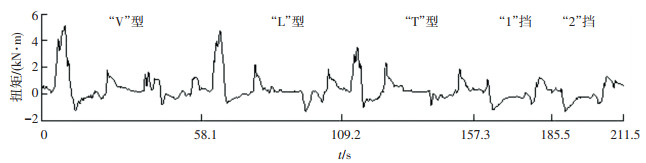
装载机铲装过程中作业方式改变多,频繁换挡,即使在同一作业工况下工作,不同作业过程之间的载荷性质(方向、均值、幅值和交变程度等)也会有很大差别[13-14].载荷数据处理过程中需要充分考虑挡位因素,挡位的差异使传动系统传递的载荷各异,如何合理构建在不同工况下不同挡位所对应的载荷数据是后续台架试验加载的关键[3, 15].进行了多个工况的非平稳随机载荷时间历程及相应挡位压力测试,其中一组载荷数据曲线如图 2所示.通过数据分析可知,换挡过程载荷幅值变化具有单调性.在大量试验数据分析基础上,提出以下两个指标作为选用加载换挡过程典型载荷构建对象的依据:
|
图 2 多个工况挡位压力和扭矩载荷时间历程曲线 Fig. 2 Time history curve of multiple operating range pressure and torque loads |
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta T = {T_{\max }} - {T_{\min }}}\\ {\tan \theta = \left( {T\left( {{t_0} + \Delta t} \right) - T\left( {{t_0}} \right)} \right)/\Delta t} \end{array}} \right. $ | (1) |
式中:扭矩载荷最大值为Tmax,最小值为Tmin, ΔT=Tmax-Tmin, 上述指标能直观地展现不同换挡过程载荷的变化范围;tan θ为单位时间扭矩载荷变化.
在图 2数据基础上以式(1)对换挡过程变速器所受扭矩载荷进行分析, 结果见表 1.由表 1可知,载荷幅值变化剧烈发生在V型铲掘和后退换挡两个连续作业过程,与文献[2][13]对V型工况的研究相一致,验证了所提出的两个指标的可行性;因此本文以该典型换挡工况(铲掘和后退作业过程)载荷进行参数化表达.
| 表 1 换挡过程变速器载荷数据 Tab. 1 Load data of transmission during gear shifting |
对该过程随机试验样本数据的平稳性进行轮次数检验,可知信号非平稳.非平稳随机载荷经平均化处理后可以分解为非平稳的确定性分量(趋势项)与平稳的随机分量(随机项)两部分:
| $ {\mathit{T}_i}{\rm{(}}\mathit{t}{\rm{) = }}{\mathit{D}_\mathit{i}}{\rm{(}}\mathit{t}{\rm{) + }}{\mathit{S}_\mathit{i}}{\rm{(}}\mathit{t}{\rm{)}} $ | (2) |
式中:Ti(t)为某一时间历程非平稳随机载荷,Di (t)为Ti (t)中的确定性分量(趋势项),Si (t)为Ti(t)中平稳随机分量(随机项),i为作业工况数.
对于加载扭矩载荷的传动系变速器,其载荷谱为能代表各工况特征的扭矩载荷时间历程[16].如能将式(2)中各工况下的载荷信号用函数表达,则其载荷谱能实现参数化表达.
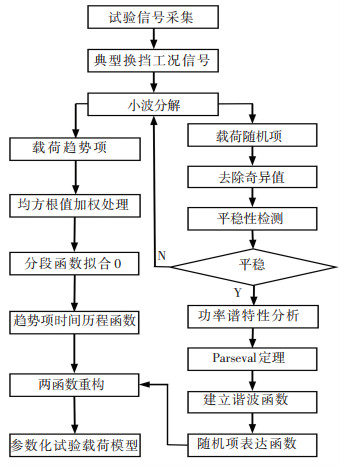
2 典型换挡工况载荷模型构建流程及相关理论 2.1 载荷模型构建流程土方机械工作过程中的外载荷数据是无法重复的、剧烈的非平稳随机信号,将试验测得的载荷进行数据处理得到其特征后才能有效地进行试验台加载和软件仿真,在此基础上构建出相应的载荷参数化表达.基于试验数据建立的典型换挡工况载荷函数重建流程如图 3所示.
|
图 3 载荷模型构建流程 Fig. 3 Process of load model construction |
传统的土方机械现场测试数据处理方法是采用随机理论,应用概率统计方法分析其扭矩统计特性,能很好地分离信号的趋势项,但难以对其进行高低频分解,无法充分揭示扭矩的频谱特征.对于实测的非平稳随机载荷信号,其在任一时刻附近的频域特征很重要,小波变换可将信号分解为不同频率的信号,并且总能量保持不变[17].小波变换是一种时间窗和频率窗均可改变的时频局部化分析方法,特别适合低频信号变化缓慢而高频信号变化迅速的非平稳信号处理, 既能分析载荷信号的整体轮廓,也可以进行信号细节分析;同时, 小波变换在保留中、高频载荷谱信号的前提下具有良好的去噪效果[18]. Wang等[19]采用小波变换对装载机V型工况载荷信号去除高斯白噪声后平稳性检验进行了分析与试验验证;郑国锋等[20]基于小波变换对汽车加速耐久性多轴载荷谱编辑方法进行了研究与验证,取得了很好的加载效果;Koszalka等[21]将小波变换应用于半挂车悬架在两种不同载荷下对实际路面动力响应的分析揭示了其响应的复杂性.
多分辨率分析作为一种重要的小波变换方法,对能量有限的载荷信号T(t)在尺度参数为2j下进行分解,通过低通滤波器得到低频分量(趋势项)Aj-1f和高通滤波器得到高频分量(随机项)Dj-1f,如式(3)所示[6]:
| $ \left\{ {\begin{array}{*{20}{l}} {{A_j}f = {A_{j - 1}}f + {D_{j - 1}}f, }\\ {{A_{j - 1}}f = \sum\limits_k {a_k^{j - 1}} \phi \left( {{2^{j - 1}}x - k} \right), }\\ {{D_{j - 1}}f = \sum\limits_k {d_k^{j - 1}} \psi \left( {{2^{j - 1}}x - k} \right).} \end{array}} \right. $ | (3) |
式中:akj-1与dkj-1分别为近似系数和细节系数;ϕ为尺度函数,与低通滤波器相对应;ψ为小波函数,与高通滤波器相对应.
根据多尺度一维小波变换的基本原理, 通过选择合适的小波函数及分解尺度进行迭代运算,实现原载荷信号的多尺度一维小波分解.
2.2.2 随机谐和函数在工程应用中,振动的能量通常集中在一定的频率范围内,超出这个频率范围的振动能量非常微小.对于土方机械的实际外载荷,可以认为在一定频率范围内基本包含了外载荷波动的全部能量,超出频率范围的谐波振动能量可以忽略不计[22].
在进行载荷随机项的仿真模拟时,可以采用一些频率、幅值、初相位都不相同的谐和函数的合成来实现[23].通过功率谱估计得到的功率谱密度P(ω)可在统计意义下描述一个载荷随机信号,将P(ω)在ω轴上分割成若干份,在满足功率谱密度函数曲线与ω轴所包含的每一个单元面积的2倍与中间频率谐和振动能量相等的条件下,可以实现随机振动能量与谐和函数表达的总能量基本相等,根据Parseval定理得[24]:
| $ \begin{array}{l} \frac{{a_n^2}}{2} = \frac{{{\omega _n} + {\omega _{n - 1}}}}{{4\pi }}\int_0^{\frac{{4\pi }}{{{\omega _n} + {\omega _{n - 1}}}}} {a_n^2} {\cos ^2}\left( {\frac{{{\omega _n} + {\omega _{n - 1}}}}{2}t - {\varphi _n}} \right){\rm{d}}t = \\ \;\;\;\;\;\;\;\;2\int_{{\omega _{n - 1}}}^{{\omega _n}} {{P_n}} (\omega ){\rm{d}}\omega . \end{array} $ | (4) |
式中:an为第n个谐波振幅, φn为第n个谐波相位角,Pn(ω)为(ωn-1, ωn)频率范围内功率谱密度.
基于式(4), 随机平稳载荷参数化表达的谐和函数为
| $ \begin{array}{l} S(t) = \sum\limits_{i = 1}^n {{a_i}} \cos \left( {{\omega _i}t - {\varphi _i}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^n {{a_j}} \cos \left( {\frac{{{\omega _{j - 1}} + {\omega _j}}}{2}t - {\varphi _j}} \right) = \\ \;\;\;\;\;\;\;\;\;\;2\sum\limits_{j = 1}^n {\sqrt {\int_{{\omega _{j - 1}}}^{{\omega _j}} {{P_j}} (\omega ){\rm{d}}\omega} \cos \left( {\frac{{{\omega _j} + {\omega _{j - 1}}}}{2} - {\varphi _j}} \right)} . \end{array} $ | (5) |
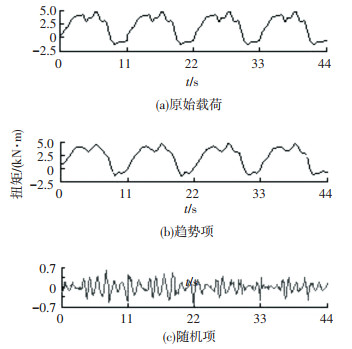
从测试的原始数据中分割出典型换挡工况的若干段载荷信号并合并为多个循环载荷历程.选用适于振动数据处理的db10小波为基本小波函数, 分解尺度为2层,小波变换分解得到的载荷趋势项和随机项如图 4所示.
|
图 4 典型换挡工况载荷小波变换分解 Fig. 4 Decomposition of wavelet transform under typical shifting condition load |
小波分解得到的载荷趋势项反映的是机器的工作模式,其形态取决于机器类型、作业对象和驾驶员的操作方式[25].在实际工作过程中,即使对操作方法和步骤做统一规定,不同工况下相同作业过程之间缓慢变化的趋势项仍存在一些差异,需对载荷数据作进一步处理.由于数据的均方根综合考虑了数据的均值与标准差[26],趋势项数据以均方根值作为分析参数,采用加权处理的方法对各子样本进行合成:
| $ {D_i}(t) = \sum\limits_{j = 1}^n {\left( {{R_{ij}}{\chi_{ij}}/\sum\limits_{j = 1}^n {{R_{ij}}} } \right)} . $ | (6) |
式中:i为不同作业段序号, j为子样本序号,n为子样本数,Rij为i作业段j子样本数据的均方根值,χij为i作业段j子样本的扭矩载荷时间序列数值.
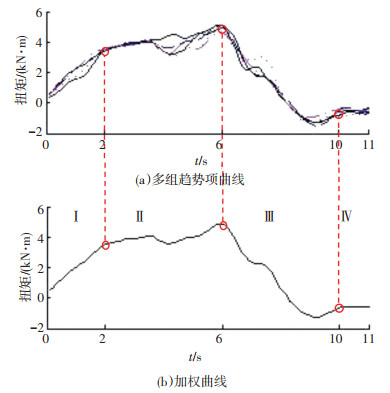
载荷数据小波分解后的趋势项和加权处理后数据中的几组曲线如图 5所示,载荷历经过程如下:前进铲过程与前进铲掘加载过程(Ⅰ和Ⅱ阶段),重载负荷下经空挡至后退挡位(Ⅲ阶段),重载平稳后退过程(Ⅳ阶段).
|
图 5 载荷趋势项加权处理前后曲线 Fig. 5 Curves before and after weighting process of load trend term |
采用合适的时域函数对趋势项数据进行拟合以实现参数化表达,通过改变能够反映机器类型、作业对象和驾驶员操作方式的函数系数,可以生成能表达不同作业过程特征的载荷时间序列,利于试验仿真和加载.本文以所选装载机典型换挡作业工况载荷历程过程特征为基础,提出趋势项函数Di(t)由分段函数来表示:
| $ {D_i}(\mathit{t}) = \\ \left\{ {\begin{array}{*{20}{l}} {{M_0} + \frac{{{M_1} - {M_0}}}{{{t_1}}}, }&{\left( {0 \le t < {t_1}} \right);}\\ {{M_1} + \frac{{{M_2} - {M_1}}}{{{t_2} - {t_1}}}\left( {t - {t_1}} \right) + A\sin \left( {2\pi \frac{{t - {t_1}}}{{{t_2} - {t_1}}}} \right), }&{}\\ {}&{\left( {{t_1} \le t < {t_2}} \right);}\\ {{M_2} - \frac{{{M_2}}}{3}{{\rm{e}}^{ - \beta {{\left( {t - {t_2}} \right)}^2}}}{{\left( {t - {t_2}} \right)}^2}, }&{\left( {{t_2} \le t < {t_3}} \right);}\\ {{M_3}, }&{\left( {{t_3} \le t < {t_4}} \right);} \end{array}} \right. $ | (7) |
式中:M0为空载接近作业对象前的扭矩;M1和M2与机器类型、作业对象等有关;M3是由机械、作业对象和操作方式共同决定的常数,M3= M2-M2exp(-β(t3-t2)2) (t3-t2)2/3; t1~t4为作业过程Ⅰ~Ⅳ的时间节点;A与驾驶员铲掘过程作业对象和操作方式有关,β与驾驶员换挡模式有关.
由式(7)得参数见表 2,β为常用的重载后退模式,其他参数与负载扭矩有关.时间参数t与驾驶员主观操作有很大关系,参数拟合所得数值不能有效地表征作业段的随机性,对原始数据进行统计分析获得时间参数t的概率密度函数,知时间参数t的分布服从对数正态分布,参数的均值和标准差如表 3.
| 表 2 趋势项参数数值 Tab. 2 Trend item parameter value |
| 表 3 时间参数t的分布参数估计 Tab. 3 Estimation of the distribution of time parameter t |
式(7)中时域时长t4作为非平稳随机循环载荷历程中的一个时域时长,可扩展时间于试验台架作循环加载.面向典型换挡工况作业段趋势项参数化表达的方法,可应用到不同作业条件下的其他工况作业段,如通过改变趋势项函数的参数来表征不同换挡工况作业段的参数化模型.
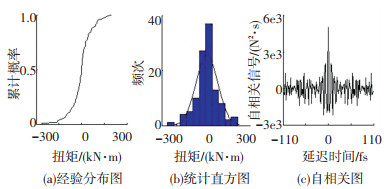
3.3 载荷随机项处理本文采用标准差检验法,将小波分解后的随机项信号中超过标准差3倍的奇异值剔除,处理后的经验分布图、直方图和自相关图见图 6,可知随机项载荷符合均值为零的正态分布且呈现平稳性特点.
|
图 6 随机项经验分布图、统计直方图和自相关图 Fig. 6 Random item empirical distribution graph, statistical histogram and autocorrelation graph |
若一个随机过程各样本是平稳的且获得各样本的试验条件基本相同,则平稳随机过程可当作各态历经过程来处理,其统计特征具有代表性[27].目前,工程应用中对各态历经平稳性检验主要采取轮次法.假设数据是平稳的,在子样数N=10,显著水平α=0.05条件下,查轮次分布表可知最小轮次数为3,最大轮次数为8,统计的载荷随机项轮次数5在区间(3, 8)内,平稳性假设成立,说明该信号数据是平稳的,可以当作各态历经过程来处理.
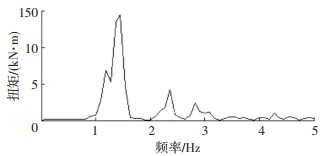
采用非参数化功率谱估计的Welch方法得到的载荷随机项的功率谱如图 7所示,知扭矩载荷波动的功率谱能量基本分布于0~5 Hz的频率范围内,峰值频率位于1.5 Hz左右,呈现低频振动特性.
|
图 7 载荷随机项功率图 Fig. 7 Power spectral density of load random term |
由式(6)可构建载荷随机项参数化表达式
| $ S(t) = \sum {{a_j}} \cos \left( {{\omega _j}t - {\varphi _j}} \right) $ |
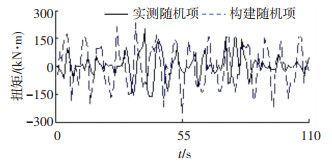
式中j=1, 2, …, 10.以图 7所示频率范围0~5 Hz,根据Parseval定理近似得到各谐波分量幅值和对应频率.信号初始相位角φj在0°~360°随机产生,通过程序模拟得到的一组随机项与实测随机项对比如图 8所示,两者振幅最值和均值比较接近且符合正态分布,参数化表达使用的谐和函数在一定程度上能复现载荷随机项的平稳随机性特征.
|
图 8 实测随机项和构建随机项对比图 Fig. 8 Comparison of measured random items and constructed random items |
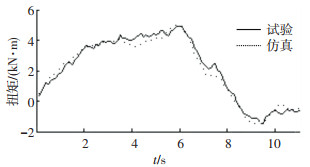
为验证该方法的可行性,在相同试验条件下得典型换挡工况作业段载荷数据,将参数化试验载荷模型随机生成的仿真数据与试验得到的一组数据对比,由图 9可知, 载荷参数化表达模型的仿真数据与试验测试载荷数据变化趋势一致,有很高的相关性,能较准确地表征典型作业过程的载荷特征.对仿真数据在子样数N=10、显著水平α=0.05条件下进行轮次性检验,可知其为非平稳数据,进一步验证了参数化试验载荷模型表达方法的有效性.
|
图 9 仿真载荷数据与试验载荷数据对比 Fig. 9 Comparison between simulated and test loads |
表 4为基于传统随机理论的多项式拟合处理方法与小波变换后参数化表达方法对试验载荷关键点的数据对比.由表 4可知,小波变换级数分解基础上的参数化试验模型比传统随机理论多项式拟合方法更为精确.
| 表 4 本文方法与传统方法构建载荷关键点数据对比 Tab. 4 Comparison of key points data of load constructed by this method and traditional method |
1) 具有非平稳随机特征的装载机典型换挡工况的载荷数据通过小波变换分解为非平稳的趋势项和平稳的随机项,分段函数拟合的趋势项能有效地反映作业工序的载荷时间历程,谐和函数参数表达的随机项能较好地表征其平稳随机特征.
2) 趋势项函数与随机项函数重构的试验载荷模型表达,在时间参数t服从对数正态分布条件下可以快速生成能够反映装载机典型换挡工况下非平稳随机载荷特征的仿真数据.
3) 小样本验证的参数化表达载荷模型,能较准确地反映原载荷非平稳随机循环特征.
| [1] |
王安麟, 岳滨楠, 周鹏举, 等. 工程机械液压泵和马达模型的非线性改进[J]. 同济大学学报(自然科学版), 2011, 39(8): 1212. WANG Anlin, YUE Binnan, ZHOU Pengju, et al. Nonlinear improvement on hydraulic pump and motor models for construction machinery[J]. Journal of Tongji University(Natural Science), 2011, 39(8): 1212. DOI:10.3969/j.issn.0253-374x.2011.08.021 |
| [2] |
张英爽, 王国强, 王继新, 等. 工程车辆传动系载荷谱编制方法[J]. 农业工程学报, 2011, 27(4): 179. ZHANG Yingshuang, WANG Guoqiang, WANG Jixin, et al. Compilation method of power train load spectrum of engineering vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(4): 179. DOI:10.3969/j.issn.1002-6819.2011.04.031 |
| [3] |
陈欣, 项昌乐. 车辆传动系多工况随机载荷谱的统计处理方法[J]. 汽车工程, 1999, 21(4): 232. CHEN Xin, XIANG Changle. Statistical methods for random load spectrum of vehicle transmission under multiple working conditions[J]. Automotive Engineering, 1999, 21(4): 232. DOI:10.19562/j.chinasae.qcgc.1999.04.008 |
| [4] |
BESSOUS N, ZOUZOU S E, BENTRAH W, et al. Diagnosis of bearing defects in induction motors using discrete wavelet transform[J]. International Journal of System Assurance Engineering & Management, 2018, 9(4): 1. DOI:10.1007/s13198-016-0459-6 |
| [5] |
YU Xiufen, XU Ke, TANG Yueying, et al. Development and realization of a novel type of high-speed windowed complex FFT processor[J]. Optik - International Journal for Light and Electron Optics, 2015, 126(14): 1381. DOI:10.1016/j.ijleo.2015.02.090 |
| [6] |
姜涛, 付志翼, 王安麟. 一种非平稳随机循环工况下的参数化载荷模型[J]. 东北大学学报(自然科学版), 2016, 37(6): 845. JIANG Tao, FU Zhiyi, WANG Anlin. Parameterized load model under non-stationary random cyclic conditions[J]. Journal of Northeastern University(Natural Science), 2016, 37(6): 845. DOI:10.3969/j.issn.1005-3026.2016.06.018 |
| [7] |
WEI Yongxiang, ZHU Haoyue, TANG Heng, et al. Compilation of load spectrum of loader drive axle[J]. Materials Science and Engineering, 2018, 322: 072059. DOI:10.1088/1757-899X/322/7/072059 |
| [8] |
ZHANG Hong, FENG Guodi, ZHANG Haijun, et al. Study on test and preparation of load spectrum of hydraulic excavator[C]// International Conference on Electronics & Information Engineering. London: ICEIE, 2017: 103223J-1. DOI: 10.1117/12.2266910
|
| [9] |
王健, 姜德艳, 周健, 等. 纯电动汽车传动系统载荷谱研究[J]. 汽车工程师, 2018(9): 30. WANG Jian, JIANG Deyan, ZHOU Jian, et al. Research on load spectrum of electric vehicle drive system[J]. Auto Engineer, 2018(9): 30. DOI:10.3969/j.issn.1674-6546.2018.09.008 |
| [10] |
MARKUS S, OLIVER K, JUERGEN W.Green wheel loader-operating strategy of an energy efficient hybrid drive train[C]//SAE 2014 Commercial Vehicle Engineering Congress. Detroit: SAE, 2014. DOI: 10.4271/2014-01-2400
|
| [11] |
OH K S, YUN S, KIM H, et al. Development of wheel loader dynamic simulation model[C]//SAE 2013 World Congress & Exhibition. Detroit: SAE, 2013: DOI: 10.4271/2013-01-1194
|
| [12] |
WANG Jixin, WANG Zhenyu, YU Xiangjun, et al. Establishment method of a mixture model and its practical application for transmission gears in an engineering vehicle[J]. Chinese Journal of Mechanical Engineering, 2012, 25(5): 1001. DOI:10.3901/CJME.2012.05.1001 |
| [13] |
许纯新, 张云龙, 诸文农. 具有分段作业特点的非平稳随机载荷的制谱方法研究[J]. 机械工程学报, 1993, 29(2): 46. XU Chunxin, ZHANG Yunlong, ZHU Wennong. Study on load spectrum preparation of non-stationary random load with sectional operating characteristics[J]. Chinese Journal of Mechanical Engineering, 1993, 29(2): 46. DOI:10.1007/BF02943552 |
| [14] |
张云龙, 诸文农, 殷涌光, 等. 装载机驱动桥半轴随机载荷分析及其载荷谱编制方法探讨[J]. 工程机械, 1988, 19(8): 19. ZHANG Yunlong, ZHU Wennong, YIN Yongguang, et al. Random load analysis of drive axle shaft in shovel loader and a study of load spectrum preparation[J]. Construction Machinery and Equipment, 1988, 19(8): 19. |
| [15] |
刘彦龙, 邹喜红, 石晓辉, 等. 基于挡位的汽车传动系载荷谱提取与外推[J]. 重庆理工大学学报(自然科学版), 2015(4): 17. LIU Yanlong, ZOU Xihong, SHI Xiaohui, et al. Extraction and extrapolation of load spectrum data for auto transmission based on gears[J]. Journal of Chongqing University of Technology(Natural Science), 2015(4): 17. DOI:10.3969/j.issn.1674-8425(z).2015.04.004 |
| [16] |
CARBONI M, CERRINI A, JOHANNESSON P, et al. Load spectra an analysis and reconstruction for hydraulic pump components[J]. Fatigue and Fracture of Engineering Materials and Structures, 2008, 31(3/4): 251. DOI:10.1111/j.1460-2695.2008.01221.x |
| [17] |
李慧浩, 许宝杰, 左云波, 等. 基于小波变换和EMD方法提取趋势项对比研究[J]. 仪器仪表与分析监测, 2013(3): 28. LI Huihao, XU Baojie, ZUO Yunbo, et al. The comparative study of the signal trend extraction based on wavelet transformation and EMD method[J]. Instrumentation Analysis Monitoring, 2013(3): 28. DOI:10.3969/j.issn.1002-3720.2013.03.010 |
| [18] |
刘海鸥, 张国鑫, 席军强, 等. 履带车辆传动系统动态载荷谱信号去噪[J]. 吉林大学学报(工学版), 2017, 47(1): 42. LIU Haiou, ZHANG Guoxin, XI Junqiang, et al. Dynamic load spectrum signal de-noising of tracked vehicle transmission[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 42. DOI:10.13229/j.cnki.jdxbgxb201701007 |
| [19] |
WANG Jixin, HU Ji, YAO Mingyao, et al. Time domain characteristics analysis of load spectrum of axle shaft[C]// IEEE International Conference on Information & Automation. Harbin: IEEE, 2010: 2061. DOI: 10.1109/ICINFA.2010.5512484
|
| [20] |
郑国峰, 上官文斌, 韩鹏飞, 等. 基于小波变换的汽车零部件加速耐久性多轴载荷谱编辑方法研究[J]. 机械工程学报, 2018, 54(10): 156. ZHENG Guofeng, SHANGGUAN Wenbin, HAN Pengfei, et al. Study of multi-axis load spectrum edition method based on the wavelet transform to the accelerated durability test of the vehicle components[J]. Journal of Mechanical Engineering, 2018, 54(10): 156. DOI:10.3901/JME.2018.10.156 |
| [21] |
KOSZALKA G, HUNICZ J, RYSAK A, et al. Nonlinear vibration of semitrailer suspension: wavelet and multiscale entropy-based approaches[J]. Archive of Applied Mechanics, 2016, 86(4): 761. DOI:10.1007/s00419-015-1060-1 |
| [22] |
CRANDALL S H, MARK W D. Random vibration in mechanical systems[M].Random vibration in mechanical systems. Pittsburgh: Academic Press, 1963: 103
|
| [23] |
陈建兵, 李杰. 随机过程的随机谐和函数表达[J]. 力学学报, 2011, 43(3): 505. CHEN Jianbing, LI Jie. Stochastic harmonic function and spectral representations[J]. Chinese journal of theoretical and applied mechanics, 2011, 43(3): 505. DOI:10.6052/0459-1879-2011-3-lxxb2010-375 |
| [24] |
马登成, 杨士敏, 马登慧, 等. 工程机械波动载荷分析与模拟方法研究[J]. 甘肃农业大学学报, 2013, 48(3): 136. MA Dengcheng, YANG Shimin, MA Denghui, et al. An analysis of fluctuations load and simulation method on construction machinery[J]. Journal of Gansu Agricultural University, 2013, 48(3): 136. DOI:10.3969/j.issn.1003-4315.2013.03.026 |
| [25] |
王安麟, 石世宁, 李晓田. 挖掘机动态性能试验及其数据的小波处理方法[J]. 同济大学学报(自然科学版), 2014, 42(1): 0115. WANG Anlin, SHI Shining, LI Xiaotian. Dynamic performance test and wavelet processing method for non-stationary random data of hydraulic excavator[J]. Journal of Tongji University(Natural Science), 2014, 42(1): 0115. DOI:10.3969/j.issn.0253-374x.2014.01.019 |
| [26] |
徐礼超, 葛如海, 常绿. 典型工况下装载机液压系统载荷时间历程的制取方法[J]. 农业工程学报, 2012, 28(6): 57. XU Lichao, GE Ruhai, CHANG Lü. Acquisition method of load time course of loader hydraulic system under typical operating conditions[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(6): 57. DOI:10.3969/j.issn.1002-6819.2012.06.010 |
| [27] |
HEULER P, KLATSCHKE H. Generation and use of standardised load spectra and load time histories[J]. International Journal of Fatigue, 2005, 27(8): 974. DOI:10.1016/j.ijfatigue.2004.09.01 |
 2020, Vol. 52
2020, Vol. 52


